绝对重力仪研制中一种新的自由落体轨迹重建算法*
2012-09-15琼滕云田黄大伦龙剑锋
吴 琼滕云田黄大伦龙剑锋
1)中国北京100081中国地震局地球物理研究所
2)中国北京100013中国计量科学研究院
绝对重力仪研制中一种新的自由落体轨迹重建算法*
吴 琼1),滕云田1)黄大伦2)龙剑锋1)
1)中国北京100081中国地震局地球物理研究所
2)中国北京100013中国计量科学研究院
真空系统中落体做自由下落运动的轨迹重建算法,是进行拟合求解绝对重力测量结果的关键步骤之一.在自主研制小型高精度激光干涉绝对重力仪的过程中,基于目前高速发展的数字测量技术,提出一种自由落体轨迹重建的算法.其基本原理是:首先通过高速采样,得到落体自由下落过程中产生的一系列数字化的激光干涉信号;其次通过数字处理算法提取干涉信号每次过零前后采样点的时间坐标;然后按照相同的下落高度均分这些过零点,得到落体运动轨迹上的“时间-位移”坐标,从而重建落体轨迹.模拟实验表明,该算法时间平均误差在±0.01 ns范围以内,由此引入的计算测量重力加速度平均误差为5.2×10-12m/s2,一次完整测量循环的时间为15 s,计算时间为2.5 s.该结果保证了高精度绝对重力仪研制中对测量速度和计算精度的要求.
绝对重力仪 自由落体 过零点计算 轨迹重建
Abstract:Rebuilding the trace of a free-fall body in the vacuum is one of the key steps in finding gravitational acceleration from the sampled fringe signals.This paper proposed an algorithm for rebuilding the trace during the independent process of developing small Laser Interference Absolute Gravimeter.The basic principles are:①Computing the time of the points before and after zero-crossing of a completely sampled fringe signal,which is generated by a freely falling body,and getting the time coordinates of zero-crossing points;②Dividing these time coordinates to get the Time-Displacement Coordinates in the bodytrace using the same displacement interval.In the experiment,we found that it needs 2.5 s to complete one calculation,the average timing accuracy is ±0.01 ns,the induced error is 5.2×10-12m/s2,and one complete measurement time is 15 s.The results satisfy the demand of the measurement speed and the accuracy in developing the high precision laser interference absolute gravimeter.
Key words:absolute gravimeter;free-fall body;calculation of zero-crossing;trace rebuilding
引言
绝对重力仪是一种高精度的重力加速度绝对值(10-8m/s2)测量设备,广泛应用于地震监测(刘栋勋,刘文泰,1984;游泽霖,徐菊生,1984;Simon et al,2001),地热资源探测(Sugihara,2003),海平面测量(Vilibic,1997),相对重力仪的标定(Hinderer et al,1991),资源探测(张善法等,2009),以及潜艇的导航和导弹制导系统(程力等,2007;郭有光等,2003)等领域.一般绝对重力仪按照落体的运动方式可以分为上抛法和下落法(Sakuma,1984;Rothleitner et al,2009),g值的确定是通过追踪计算位于真空室内做自由下落(或上抛)运动的落体(或抛体)的运动轨迹得到的.算法的主要过程是首先获得落体相对于参考点位置(参考棱镜)信息的干涉带信息,然后提取干涉带上包含的落体运动的信息,通过最小二乘拟合获得仪器归算点处的重力加速度值(Durando et al,2002).这个过程中落体运动信息的提取精度是保证结果精度的前提.2009年第8次国际绝对重力仪比对大会上,基于原子干涉的绝对重力仪第一次出现(de Angelis et al,2009).这种仪器是通过磁光阱冷却原子云团,从而提取原子团自由下落时感受的重力场信息.这种测量方式从原理上与激光干涉法测量的精度处于同一量级.
激光干涉绝对重力仪中,对干涉带的处理可以分为硬件和软件两类.美国的JILA-g以及FG5系列重力仪均是基于硬件的过零触发法提取干涉带的过零点信息(Zumberge et al,1982;Van Camp et al,2003).其主要过程是通过过零检测器检测干涉带的过零点,然后将干涉带过零时产生的每N个脉冲信号生成1个脉冲,送入与外部铷原子钟同步的时间间隔分析仪中,从而测量每N个干涉带所经历的时间间隔.这种方法主要是通过硬件的方式提取落体运动轨迹上的时间-位移对,然后利用最小二乘原理拟合落体运动轨迹,计算重力加速度.
随着现代数字技术的高速发展,干涉带的数字化处理与基于硬件的过零触发处理电路相比,有着硬件系统和处理算法简单、误差小、模块化的优势.意大利学者D’Agostino等提出了一种数字化干涉带处理算法局部拟合算法(D’Agostino et al,2005,2008),通过数字处理算法提取干涉带上落体感受到的重力作用信息.Bich等(2007)对该算法的测量误差进行了详细分析.该算法首先通过高速数字化仪对干涉带信号进行采集,然后写出一个带有重力加速度变量的函数方程,通过总体最小二乘算法,与干涉带信号直接拟合求解g值.为了减小误差,将干涉信号分成若干段,每段内利用函数方程拟合干涉波形,直接求解g值.由于每段包含了很短的采样时间,故可以认为每段内干涉信号的频率恒定,这样的近似的确可以减小调频带来的误差.但实际落体下落过程中,干涉带的频率随下落距离的加大而加快,局部拟合算法基于段内干涉带波形频率固定的假设和对整个下落距离干涉带拟合,无疑会增加算法的误差和计算时间.
本文首先描述了笔者所在的研究团队设计绝对重力仪的数据采集系统,然后介绍了该系统提出的一种全新的落体轨迹重建算法.该算法利用数字处理算法,提取数字化的干涉带过零点信息,重建落体运动轨迹.通过模拟实验,得到了这种算法的计算精度和所需时间.结果表明,这种算法在保证精度的前提下提高了运算速度,实现了对落体轨迹精确重建.最后给出了实验样机在2011年5月21日—6月2日的实验结果.
1算法原理
在地球重力场作用下,真空系统中落体做自由下落运动时,反应落体位置信息的干涉光束被光电接收器接收.光电接收器输出电信号被高速数字化仪接收,转变成数字信号后保存在数字化仪的内存中.数字化仪的时间基准用外部铷原子钟锁定,如图1所示.本系统采用的光源为基于非饱和蒸汽压的碘稳定633 nm He-Ne激光系统,工作时锁定在I2分子饱和吸收谱线的f峰(钱进等,2008),频率日长期稳定性优于5×10-11;光电接收器频带为4 kHz—80 MHz;铷原子钟频率重现性小于5×10-11,稳定度小于1×10-11/s;高速数字化仪采样频率为62.5 MHz,时间基准通过锁相环由外部铷原子钟提供,板载内存128 M,字长8位.
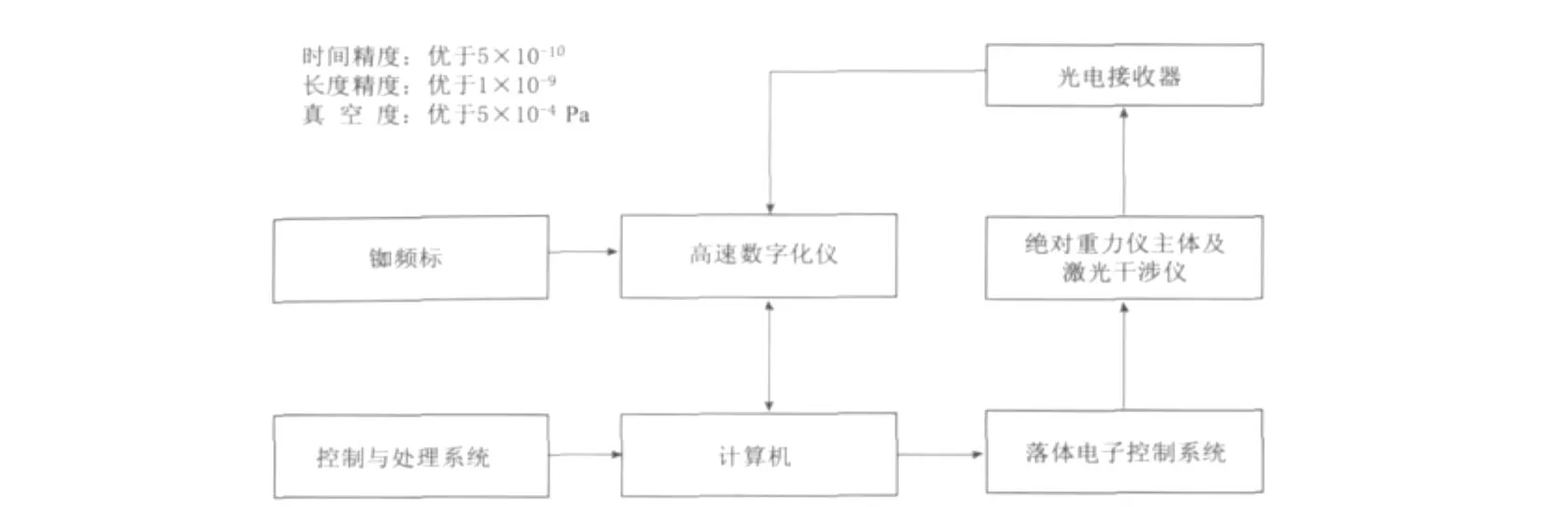
图1 算法中的功能模块连接示意图Fig.1 Relationship between the function modules in the algorithm
落体相对于参考棱镜位置信息的干涉带波形可以认为是调频的正弦波,其瞬时频率随着落体下落的速度的增加而不断增加,下落的位移与干涉带波形瞬时频率的关系可以表示为

式中,λ为激光波长,本研究中的激光波长取633 nm;f为干涉带波形的瞬时频率;T为瞬时周期;s为落体自由下落的位移;g为重力加速度(1g=9.8 m/s2).
由此可以计算出,当计算的落体下落距离为1—18cm时,干涉带的频率范围为1.4—5.9 MHz.为了从得到的数字干涉带波形中重建落体的下落轨迹,需要计算落体在某个时刻的下落距离.由于落体每下落半个激光波长,就会产生一条完整的干涉带波形,同时数字化仪的时间基准来自于外部的铷原子钟,因此可以通过计算一个完整的正弦波上的采样点来得到落体运动轨迹上的时间-位移坐标,进而重建落体的下落轨迹.
因为干涉带波形是一种调频的正弦波形,同时又混入了各种背景噪声,为了保证计算的精确度,可以通过计算信号斜率最大的过零点位置来重建落体的下落轨迹.在计算中,我们将落体的整个下落过程分成L段,每段中包含N个过零点,即每段对应落体下落的距离为

式中,S为每段对应落体自由下落的距离;N=400,为每段中包含的干涉带过零点次数;λ=633 nm,为激光波长.由此可以计算出每段落体自由下落的位移约为0.06mm.
由于每段内部我们仅需要统计干涉带波形的过零点次数,所以不需要对每个过零点都精确计算其过零点时刻.因此,我们仅对每段的第一个过零点进行精确计算,具体计算过程如下:
1)首先设定一个噪声上限阈值T,将绝对值大于T的采样点组成一个新的时间序列Xnew,计算Xnew的过零点次数,然后提取每次过零点的前一个和后一个幅值大于T坐标,组成两个新的时间序列Xind1和Xind2.图2分别给出了过零点前(圆圈)和过零点后(星号)得到的Xind1和Xind2.Xind1的长度就是总过零点的个数.
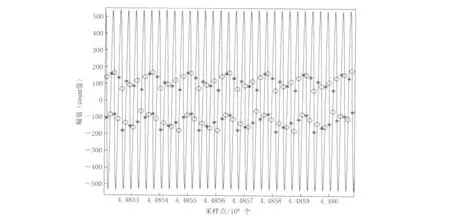
图2 过零点算法结果(过零点前用圆圈表示,过零点后用星号表示)Fig.2 Result of the zero-crossing algorithm.Circles stand for the points before zero-crossing points,and stars denote the points after zero-crossing points
2)设定总段数L和每段内过零点的个数N,由此确定每段落体的位移为S=(N-1)/2 ×(λ/2),总位移为s=S×L;
3)利用Xind1和Xind2计算每段第一个过零点的准确时刻.设干涉带的采样率为fs,对于第i段第一个过零点,该时刻的准确计算可以分为以下3种情况:
a 如果Xind2(i)与Xind1(i)之间无采样点,则该时刻为
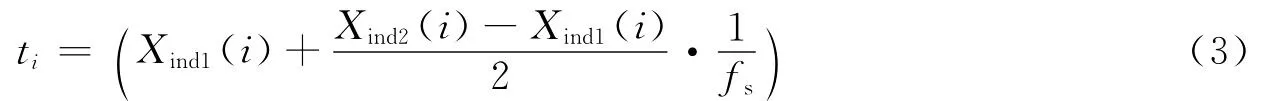
b 如果Xind2(i)与Xind1(i)之间仅有一个采样点,在原始时间序列中的下标为k,则该时刻为

c 如果Xind2(i)与Xind1(i)之间多于一个采样点,则对Xind2(i)与Xind1(i)之间的所有点进行置零,在Xind2(i)与Xind1(i)之间进行线性插值,设得到的插值曲线上最接近零的点下标为k,则该时刻为

2 模拟计算轨迹重建算法的精度
为了得到本文第一部分中描述的算法精度和效率,首先在双核、4GB RAM的硬件环境测试.本算法采样、计算总时间不超过15s,纯计算时间不超过2.5s,如果考虑系统稳定性要求而等待的时间,40s内可以完成一次测量,每小时可以进行约90次测量.然后利用第一部分的计算过程1),通过不同频率的正弦波来模拟落体在不同下落位置时产生的干涉带信号,计算本算法在各个频点处的误差.
具体过程为:首先将铷原子钟输出的10MHz标准正弦波送入频率综合器,然后利用频率综合器输出不同频率的正弦波信号,通过集成有本算法的数字采集与处理系统分析计算这些正弦波信号,从而估计算法精度.这里用于实验的频率综合器的输出正弦波的时间误差与外部铷原子钟的时间不确定性一致.采集L段这样的正弦波,每段内有N个过零点,即(N-1)/2个完整的正弦波.设送入数字化仪的正弦波脉冲频率为f,采样频率为fs,则每段正弦波对应的标准时间可以表示为

通过第一部分的算法,可以计算每段正弦波起始点到终止点之间的采样点个数为n,则这段波形对应的时间可以表示为

则算法的时间误差可以表示为

由此引入的绝对重力加速度值的计算误差可以表示为
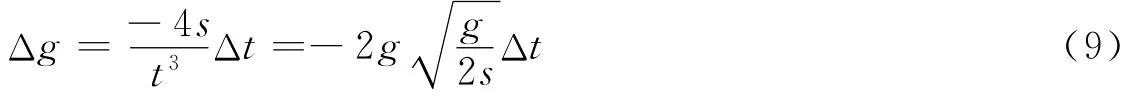
正弦波输入数字化仪后,采集1000段,每段400个过零点,由式(8)计算得到1000段累积时间误差、最大时间误差、最小时间误差和平均时间误差.图3显示了落体从2cm即干涉带瞬时频率为1.98MHz开始,下落至18cm的过程中不同频率点处算法的累积,最大和最小时间误差,以及由此引入的测量误差.
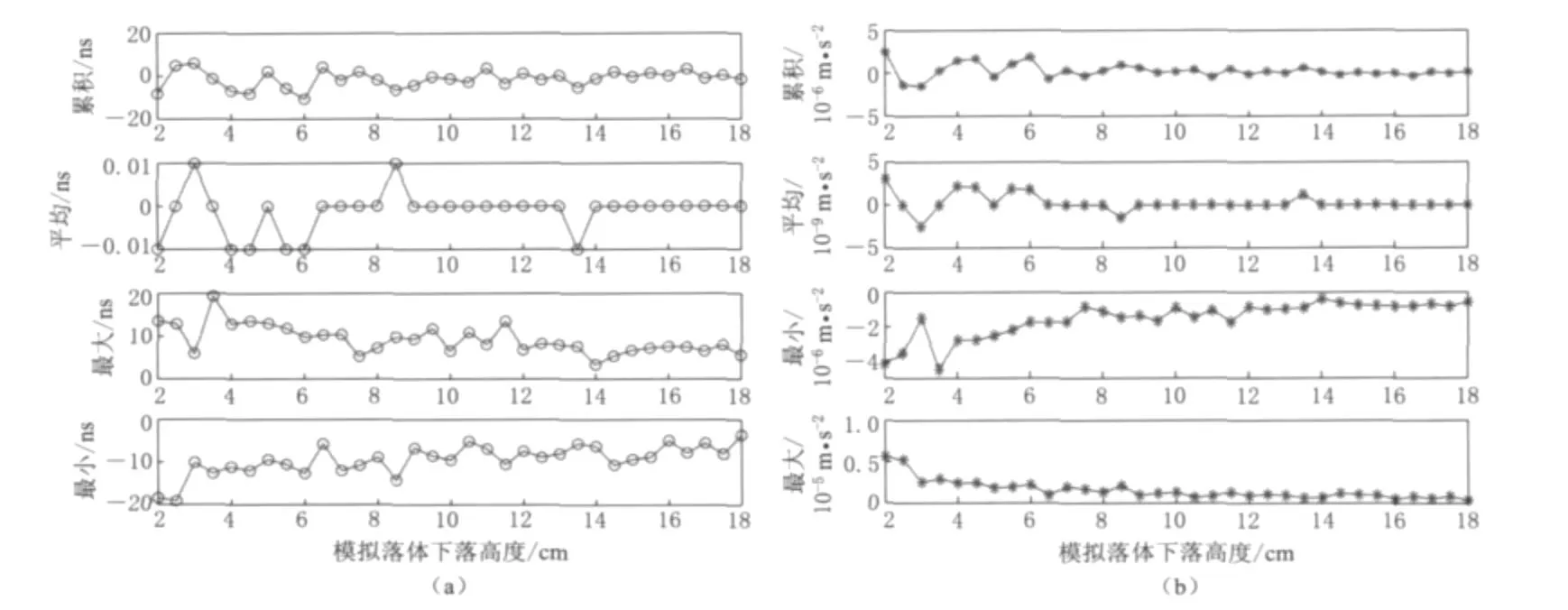
图3 算法时间误差(a)以及由此引入的测量误差(b)估计Fig.3 Estimation of the algorithm time(a)and measurement(b)errors
通过利用式(1)和式(9)对算法时间误差的估计发现,落体下落的高度在2cm之前,算法误差较大;当落体下落的高度超过2cm后,算法的累积时间误差稳定在±20ns之间;而当落体下落高度大于6cm时,累积时间误差稳定在±10 ns之间.
由于实际干涉带波形的频率随着下落高度的增加而增加,在相同的时间段内,低频段的过零点个数要远远小于高频段,因此其过零点计算误差对计算结果影响远小于高频段.因此在计算该算法在落体整个下落过程中误差的综合时,可以根据频率设计一个加权系数,即

式中,fi是某个高度对应的干涉带信号瞬时频率,wi为该频率对应的权系数.表1给出了落体在1—18cm段、2—18cm段和6—18cm段内算法对应的综合时间误差和由此引入的综合测量误差.

表1 算法综合误差Table 1 Total error of the algorithm
从表1的实验结果可以看出,在平均误差方面,算法的综合误差随着落体下落距离的增加呈现明显的减小趋势,但是均非常接近与零.而算法在累积、最大和最小综合误差方面,从2—18cm和6—18cm两个下落段的计算结果中看,没有明显的改善.这从一个方面证明了,在干涉带频率比较低时,虽然算法误差较大,但是由于过零点个数不多,算法的误差没有给结果带来明显的计算误差.因此,可以利用该算法从落体下落2cm时开始取数计算,尽量增加有效的数据量,提高测量结果的可靠性.
3 实验观测结果与结论
2011年5—6月,笔者所属研究小组使用基于本文介绍的轨迹重建算法的实验样机在北京国家地球观象台进行了试验观测.为研究落体次数对观测精度的影响,在该台的国家重力基准点(编号H03,基岩点)分别进行了320次下落和160次下落的两次观测.同时作为抗干扰观测试验,在该台的普通办公室设置重力点(编号H09,地板点)也进行了一次320次下落的测量.H03测点参考值采用FG5/232在2009年和2010年的观测结果的平均值,H09测点的参考值采用两套高精度相对重力仪(联测精度10×10-8m/s2)与H03测点联测得到.H09和H03两点的参考重力值均根据梯度测量结果归算到实验样机0.6m的有效高度.表2给出了这2个测点的3次测量结果与各测点的参考值之间的偏差与测量精度.

表2 2011年5月实验样机测量结果Table 2 Measurement results in the test of May 2011
结果表明,基于本文算法的实验样机精度在160次测量时即优于10×10-8m/s2,系统偏差约71×10-8m/s2,H09测点两次测量系统偏差固定.这一结果为下一步进行系统差的确认和研发更高精度的绝对重力仪提供了技术保障.
本文基于自主研制的数字化绝对重力仪的数字化干涉带信号,提出了一种全新的数字处理算法,它不同于目前国际上流行的基于硬件的过零点触发法和基于数字化干涉带局部拟合算法.本文算法主要针对数字化的干涉带信号,利用分段和对每段第一个过零点精确时刻的求取,提取落体下落过程中的时间位移坐标.然后通过最小二乘拟合求解重力加速度.可以说是基于硬件的过零触发法的软件替代.该设备和算法简单,误差小,采集可以实现模块化,利于系统误差的理论计算和固定,便于具有自主知识产权仪器的批量商业化生产.
程力,张雅杰,蔡体菁.2007.重力辅助导航匹配区域选择准则[J].中国惯性技术学报,15(5):559--563.
郭有光,钟斌,边少峰.2003.地球重力场确定与重力场匹配导航[J].海洋测绘,23(5):61--64.
刘栋勋,刘文泰.1984.重力预报地震动态[J].四川地震,(1):27--31.
钱进,刘忠有,张小平,石春英,刘秀英,王悍平,蔡山,谭慧萍.2008.一种新型的碘稳定633 nm He-Ne激光系统[J].计量学报,29(1):10--13.
游泽霖,徐菊生.1984.精密绝对重力测量在地震研究中的应用[J].地壳形变与地震,4(4):410--414.
张善法,孟令顺,杜晓娟,张凤旭,马国庆.2009.高精度重力测量在金矿采空区探测中的应用研究[J].地球物理学进展,24(2):590--595.
Bich W,D’Agostino G,Germak A,Pennecchi F.2007.Uncertainty propagation in a non-linear regression analysis:Application to a ballistic absolute gravimeter(IMGC-02)[C]∥Advanced Methods for Uncertainty Estimation in Measurement,2007 IEEE International Workshop:30--34.
D’Agostino G,Germak A,Desogus S,Origlia C,Barbato G.2005.A method to estimate the time-position coordinates of a free-falling test-mass in absolute gravimetry[J].Institute of Physics Publishing,42(4):233--238.
D’Agostino G,Desogus S,Germak A,Origlia C,Quagliotti D,Berrino G,Corrado G,d’Errico V Ricciardi G.2008.The new IMGC-02 transportable absolute gravimeter:Measurement apparatus and applications in geophysics and volcanology[J].Annals of Geophysics,51(1):39--49.
de Angelis M,Bertoldi A,Cacciapuoti L,Giorgini A,Lamporesi G,Prevedelli M,Saccorotti G,Tino G M.2009.Precision gravimetry with atomic sensors[J].Measurement Science and Technology,20(2):1--16.
Durando G,Desogus S,Mazzoleni F.2002.Accuracy assessment of analysis of a free-fall gravimeter data[C]∥Conference Digest 2002/Conference on Precision Electromagnetic Measurements.Ottawa,Ontario,Canada:86--87.
Hinderer J,Florsch N,Makinen J,Legros H,Faller J E.1991.On the calibration of a superconducting gravimeter using absolute gravity measurements[J].Geophys J Int,106(2):491--497.
Rothleitner Ch,Svitlov S,Merimeche H,Hu H,Wang L J.2009.Development of new free-fall absolute gravimeters[J].Metrologia,46(3):283--297.
Sakuma A.1984.Present status of the absolute measurement of gravitational acceleration[G]∥Taylor B N,Phillips W D eds.Precision Measurement and Fundamental ConstantsⅡ.Washington,D C:U S Government Printing Office:397--404.
Simon D P,Williams,T F.Graham Jeffries B.2001.Absolute gravity measurements at UK tide gauges[J].Geophys Res Lett,28(12):2317--2320.
Sugihara M.2003.Geothermal reservoir monitoring with an FG5 absolute gravimeter[C]∥Proceedings,Twenty-Eighth Workshop on Geothermal Reservoir Engineering.Stanford University,Stanford,California.
Vilibic I.1997.Global sea level rise?New techniques for the absolute sea level measurement[J].Geofizika,14:119--131.
Van Camp M,Camelbeeck T,Richard P.2003.The FG5 absolute gravimeter:Metrology and geophysics[J].Physicalia Magazine,Journal of the Belgian Society,25(3):161--174.
Zumberge M A,Rinker R L,Faller J E.1982.A portable apparatus for absolute measurements of the earth’s gravity[J].Metrologia,18(3):145--152.
A new type of algorithm for rebuilding the trace of free-fall body in absolute gravimeter development
Wu Qiong1),Teng Yuntian1)Huang Dalun2)Long Jianfeng1)
1)Institute of Geophysics,China Earthquake Administration,Beijing 100081,China
2)National Institute of Metrology P.R.China,Beijing 100013,China
10.3969/j.issn.0253-3782.2012.04.011
P315.61
A
中国地震局地球物理研究所基本科研业务费(DQJB01A02)资助.
2011-06-23收到初稿,2012-01-04决定采用修改稿.
e-mail:wuqiong_cea@hotmail.com
吴琼,滕云田,黄大伦,龙剑锋.2012.绝对重力仪研制中一种新的自由落体轨迹重建算法.地震学报,34(4):549--556.
Wu Qiong,Teng Yuntian,Huang Dalun,Long Jianfeng.2012.A new type of algorithm for rebuilding the trace of free-fall body in absolute gravimeter development.Acta Seismologica Sinica,34(4):549--556.
