1976年唐山MS7.8地震余震序列持续时间及对地震危险性分析的意义＊

仲 秋 史保平

（中国北京100049中国科学院研究生院地球科学学院）

1976年唐山MS7.8地震余震序列持续时间及对地震危险性分析的意义＊

仲 秋 史保平

（中国北京100049中国科学院研究生院地球科学学院）

1976年7月28日唐山MS7.8大地震对唐山及其周边地区造成了重大的人员伤亡和财产损失.主震之后约15小时滦县又发生了MS7.1地震；同年11月15日宁河也发生了MS6.9地震.唐山MS7.8主震后的余震一直持续至今，使该区域至今保持了与主震前相比具有较高的地震活动性.如何估计余震的持续时间，并进一步将余震从主震目录中去除，一直是地震学中所关注的问题.该文通过对数线性回归和理论计算，从不同角度求取并讨论了1976年唐山MS7.8大地震的余震持续时间.结果表明，由对数线性回归计算得到的余震持续时间约为80 a.而基于Dieterich的余震触发理论所得到的余震持续时间则与区域剪应力变化率有关.区域剪应力变化率可有几种不同方法求得：①根据剪应力变化率和静态应力降Δτe及地震回复周期tr之间的关系求取应力变化率，该方法所得到的余震持续时间约为70—100 a；②Ziv和Rubin对Dieterich的方法进行了修正，给出了通过远场加载速率和断层宽度求取应力变化率，该方法得到的余震持续时间约为80 a；③由背景场地震活动性求取远场剪应力速率，可以得到该地区二维分布式的余震持续时间，此方法得到的研究区域内余震持续时间为130—160 a.综上，唐山地区余震持续时间约为70—140 a，据此，该地区现今所发生的地震仍为MS7.8唐山地震所触发的余震.

1976唐山地震 余震持续时间 地震触发 剪应力变化率

Abstract：The disastrous MS7.8 earthquake in Tangshan，China，on 28 July 1976 caused great damage and significant casualties.The mainshock was followed by two large aftershocks：the MS7.1 event to the northeast near Luanxian 15 h after the mainshock，and the MS6.9 event on 15 November south－west of Tangshan near Ninghe.The aftershock sequence lasts to date，making regional seismic activity around the Tangshan main fault much higher than that of before the mainshock.It is always difficult to accurately determine the duration time of aftershock sequences and identify the aftershocks from main event catalog.In this study，by using theoretical inference and empirical relation，we tried to derive the time length of aftershock sequences of the MS7.8 Tangshan earthquake.The estimated aftershock duration from a log－log regression is about 120 years according to the empirical Omori’s relation（Toda et al）.Based on Dietrich theory，it has been claimed that the aftershock duration is a function of remote shear stressing rate，normal stress acting on the fault plane，and fault frictional constitutive parameters（Dieterich）.In general，shear stressing rate could be estimated in three ways：①Shear stressing rate could be written as a function of static stress drop and a mean earthquake recurrence time（Dieterich）.In this case，the time length of aftershock sequences is about 70—100 years.However，the recurrence time inherits a great deal of uncertainty.②Ziv and Rubin derived a general function between shear stressing rate，fault slip speed and fault width with a consideration that aftershock duration does not scale with mainshock magnitude.Therefore，from Ziv’s consideration，the aftershock duration is about 80 years.③Shear stressing rate can also be described as a function of background seismicity rate（Console et al）.From this approach，a two－dimensional spatial distribution of the aftershock duration can be obtained，and the resultant time length of aftershock sequences is about 130—160 years，which is much longer than that given by previous two approaches.The conclusive noting gives that，for the 1976 MS7.8 Tangshan earthquake，the triggered aftershocks would last at least 70 years，implying that the current earthquakes which occurred in Tangshan region after the 1976 mainshock are the aftershocks of the main event.

Key words：the 1976 Tangshan earthquake；aftershock duration；earthquake triggering；shear stress rate

引言

作为一种自然现象，地震有着猝不及防的突发性以及巨大的破坏性.如何准确估算未来潜在的地震危险性，强烈地依赖于区域内地震活动性建模.众所周知，在近代地震危险性评估模型中，地震危险性分析模型一般分为确定性模型（deterministic seismic hazard analysis，简写为DSHA）和概率地震危险性评估模型（probabilistic seismic hazard analysis，简写为PSHA）.前者主要应用于重大工程设防安全系数的选取.在实际地震发生过程中，由于震源、断层破裂、地震波传播、场地影响等存有诸多不确定性，PSHA（Cornell，1968）模型被广泛应用于世界各国地震危险性分析评估计算中.而标准概率地震危险性评估模型的定量化计算主要由4个主要部分组成（Kramer，1996）：①对震源的描述；②对区域地震活动性时空变化特征的计算，即Gutenberg－Richter关系（下文简称G－R关系）；③地震动衰减关系的应用；④场地超越概率或超越频度曲线的获取.其中，G－R关系，lgλm＝a－bm（λm为震级大于或等于m的年平均次数），式中的a值和b值则由所选定的地震目录所确定，10a－bm0为震级大于等于某个震级下限m0的地震年平均发生次数，b值则描述了大震与小震次数间的比例关系.因此a和b的取值依赖于区域内部的地震活动性.在PSHA的实际建模中，泊松（Poisson）假设则是整个模型量化的基础（Kramer，1996），即所选地震目录中的各次地震是相互独立的.如果地震目录中混入了余震数据，往往会造成对a值的过高估计和b值的错误计算，从而导致相应的地震危险性的高估.如何区分研究区域内的主余震关系一直困扰着地震学界（Stein，Liu，2009）.因此，对主震后余震持续时间和触发机制的研究，可以在一定程度上解决地震目录的完整性，进一步降低概率地震危险性分析中的不确定性.另外，对余震的持续时间和触发机制的深入了解，可为建立相应的余震危险性评估模型提供恰当的物理模型.

众所周知，主震后通常在主震断层内部和周边区域伴随了大量的余震，使得区域内的地震活动性显著增加，并且余震在单位时间的次数随着时间不断衰减（～1/t，t为时间），余震次数随时间的衰减过程通常由大森（Omori）经验关系所描述.目前，对主震后余震的产生机制的认识主要来源于静态触发和动态触发.前者可归结于主震断层相互运动所造成的区域库仑应力场的变化（King et al，1994；Harris，Simpson，1998），如果作用于断层面上的库仑应力变化ΔCFS为正，那么可造成该断层的加速破裂，反之则可推后发生.这就是许多文献中所述的时钟提前，对于一个处于闭锁阶段的断层来说，时间的提前或推后量Δt≈ΔCFS/˙τ，˙τ为剪应力速率.动态应力触发准则将余震的触发归结于动态应力波对断层的影响（Gomberg et al，1998）.通过断层面的体波和面波同样可以造成断层内部状态的变化，从而导致断层摩擦失稳.一般说来，动态触发对于远场（2—3个断层距离）地震活动性的显著增加的解释渐被接受.而近场触发，则归结于静态应力场变化的影响（Parsons，Velasco，2009）.事实上，基于滑移速率和状态相依赖的摩擦准则（Dieterich，1979，1981；Ruina，1983；Rice，Gu，1983），以及单自由度的弹簧滑块模型，首次从力学上阐述了断层摩擦失稳的力学过程.Dieterich（1994）推导出了单个断层上大震发生后地震次数随时间的变化关系，即余震持续时间和断层内部结构、状态及剪应力变化率的关系等诸多重要结论，并给出了对大森余震持续衰减的物理过程的解释.Console等（2006）对滑动速率－滑动状态模型进行了进一步的研究，给出了背景场地震活动性与剪应力变化率之间的关系.基于Dieterich的理论，Toda等（1998）对1995日本阪神地震余震的影响因素和未来地震发生的可能性进行了研究，用对数线性拟合余震次数随时间的变化关系，并以拟合直线回到背景地震次数所用时间作为余震持续时间.Stein和Liu（2009）对板块内部和板缘地震余震持续时间进行了对比分析，认为余震的持续时间与震级并无直接的相关性，而是与断层面上的加载速率相关.

本文将以1976年唐山MS7.8大地震为例，采用理论计算和数据拟合，从不同角度定量估计余震持续时间，并对结果进行必要的讨论.研究结果可对区域地震定量评估提供合理的输入参数.

1 研究区域地质及地球物理背景

图1 唐山及其周边地区的地形、活动断层和1976年7月28日唐山MS7.8地震前的历史地震（a）及唐山地震后至今的地震活动（b）.图中实心圆表示MS≥2.0地震活动，实线为断层，色标显示高程信息Fig.1 Landform，active faults and historical earthquakes before（a）and after（b）Tangshan MS7.8 earthquake.Solid circles represent MS≥2.0 earthquakes，solid lines denote active faults in this region，and color bar shows elevation

1976年7月28日唐山MS7.8大地震是20世纪发生在华北地区的最大的事件.该地震对唐山及其周边地区造成了重大的人员伤亡和财产损失.主震之后约15小时滦县又发生了MS7.1地震；同年11月15日，宁河又发生了MS6.9地震.之后有大量余震发生并一直持续至今，使得该区域一直保持了与主震前相比具有较高的地震活动性（图1）.唐山MS7.8地震发生于地震较为活跃的华北盆地北缘.GPS显示该处的地壳运动速率为2—8mm/a，且主要运动方向为N120°—140°E（Wang et al，2001；Shen et al，2000）.唐山断层为一隐伏断层，震后地表主破裂带长达8km，总体走向N30°E（尤惠川等，2002）.主震震源深度为15km，断层宽度为20km（Huang，Yeh，1997；HarvardcmT网①http：∥www.globalcmt.org/CMTsearch.html）.Butler等（1979）在对唐山地震震源机制的研究中，给出了唐山地震主震为MS7.7，断裂长度为约140km，地震矩M0＝1.8×1020N·m，主震静态应力降为30×105Pa；Huang和Yeh（1997）给出的唐山地震主震震级为MS7.8，断层长度为48km，地震矩M0＝9.8×1019N·m，主震静态应力降Δτe＝（45±5.5）×105Pa；HarvardcmT网站上给出唐山地震为走滑型地震，主震震级为MS7.9，震源机制解为M0＝2.77×1020N·m.唐山地震主震平均滑动位移为3.53 m（Huang，Yeh，1997）.另外，活动构造分析表明，唐山断裂带上7级以上地震的重复周期约为3 000—4 000 a（邓起东等，1994）.静态库伦应力模型结果也表明，唐山MS7.8地震主震最大库仑应力ΔCFS变化约为2×105Pa（Robinson，Zhou，2005；万永革等，2008）.唐山MS7.8地震前，该区域（117.5—119.5°E，38.6—40.6°N）的背景场地震年发生率约为6次；唐山MS7.8地震后一年内，其年发生率骤升为422次；1978年，年发生率降为46次.从中国地震台网公布的数据表明，截止到2006年底年发生次数为17，仍远大于背景场地震次数.

2 余震触发的Dieterich理论

引发地震的主要原因可以归结为断层摩擦过程中的突发失稳.岩石力学中的摩擦实验结果表明，摩擦系数μ为断层滑动速率与断层内部接触状态的函数

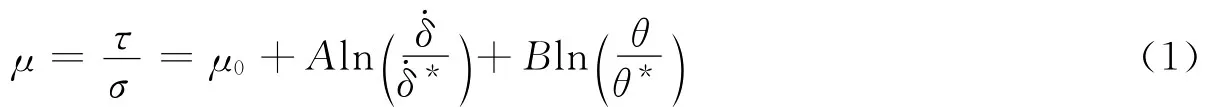
式中，τ和σ分别为断层面上的剪应力和正应力，˙δ为滑移速率，θ为滑移状态变量，μ0为一常数.˙δ＊>和θ＊>分别为参考滑移速率和状态变量值A和B，分别由实验结果给定，为一不依赖于岩石类型的量，其取值范围一般在0.005—0.010之间（Dieterich，1992）.状态变量θ随时间和滑移速率变化，描述了断层内部与接触时间相关的强化过程（aging）.其公式可表达为（Dieterich，1994）：

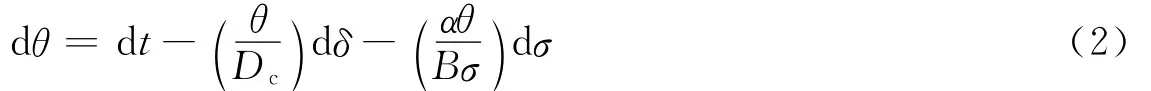
式中，δ为滑动位移；α为正应力演化状态的本构参数，一般取值为0.25.假设地震前后，作用于断层面的正应力保持不变，则有

式中，Dc为临界弱化距离，其取值一般为1—100μm（Marone，1998）.由公式（3）可以看出，dθ/d t＝0，˙δ＝θ/Dc，说明断层演化是处于一个稳定的状态.从而μss＝μ0＋（A－B）ln（˙δ/˙δ＊>）.当A－B＜0，断层运动处于滑移速度弱化的过程.反之，如果A－B＜0，则对应了滑移速度强化的过程.式中A和B的取值，可用于对断层发震深度的约束（Scholz，1998）.

进一步，假设断层的滑移过程可由一单自由度的滑块－弹簧模型来描述（Rice，Gu，1983），如图2所示，其动力学方程可写为

式中，k为弹簧的刚度系数，且k＜kc＝（B－A）/Dc（Scholz，1998）；˙δ0为远场的加载速率.数值求解方程（1）、（3）和（4），可以得到断层滑动的演化过程可由3个阶段组成（图3）：①稳定滑动阶段；②加速阶段；③瞬态失稳阶段.地震过程的同震过程对应于第3阶段，即断层的动态破裂，通常在几十秒到上百秒内完成.

从Dieterich（1994）理论可知：如果单个断层的演化阶段处于图3所示的阶段2，即加速失稳的过程，那么，θ远大于Dc/˙δ（θ≫Dc/˙δ）.因此公式（3）可写为

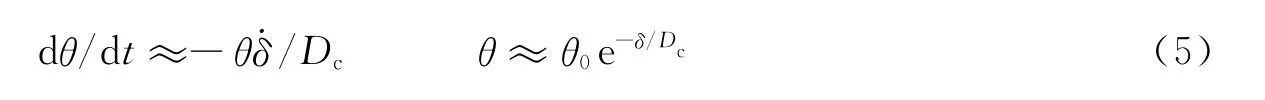
如果远场加载函数τ（t）＝τ0＋˙τt，其中˙τ为一常量.那么，由方程（1）、（4）和（5）联立求解可得

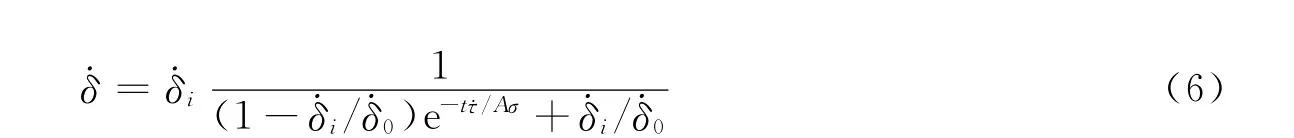
式中，˙δi为失稳时的速率.如果在这个演化阶段，断层受到来自主震过程后断层运动产生的区域静态应力场变化Δτ的扰动，那么断层上的滑动速度的变化

由应力扰动所造成的滑移速率突变，可导致断层失稳过程的提前或推后.这一点主要取决于Δτ值的正和负.图4给出了受到应力扰动后方程（7）所给出的时钟提前的示意.

图4 断层受到应力扰动后滑移速率（a）和剪应力（b）变化的时钟提前示意图图（a）中，Δt表示了如图3所示的断层演化过程中受到静态应力扰动Δτ时，原有的演化周期发生改变，造成断层的提前失稳或推后（b），即余震的触发原因.当t＞ta时，Δt≈Δτ/˙τ；t＜ta时，Δt≈Δτ/Aσ.其中，ta表征了断层演化过程中从稳态滑动到加速失稳的转折点，也反映了断层的成核期以及对应了主震后的余震持续时间Fig.4 A schematic map of the clock advance of slide velocity（a）and shear stress（b）（a）Δt shows the clock advance；（b）Delay in the seismic cycle（Fig.3）when a perturbing static stressΔτis loaded on the fault.It can also be considered as the reason for aftershock triggering.t＞ta，Δt≈Δτ/τ˙；t＜ta，Δt≈Δτ/Aσ，tais the turning point between‘phase 0’and‘phase 1’in Fig.3.It also represent the nucleation period of a fault and the time length of aftershock sequence

因此，如果已知主震前区域背景场的剪应力变化率为˙τr，背景场的地震发生率为r，并定义新的状态演化量γ0＝1/˙τr用来描述背景场的地震活动性，那么余震的发生率则可以写为R＝r/γ˙τr.描述了背景场的地震活动性.那么应力跃变后的地震活动性变化率为

如果进一步假设˙σ＝0，则

γn和γn－1分别为

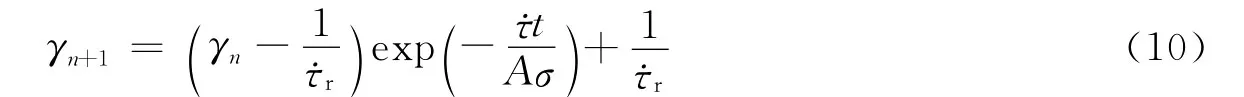
由此，我们可以得到余震随时间的发生率

而余震的持续时间有如下关系（Dieterich，1994）：

与作用于断层面上的正应力成正比，与应力的变化率成反比.在一般情况下，通常设定震后的应力变化率与震前相同，即˙τ＝˙τr，因此，ta＝Aσ/˙τr.

3 余震持续时间估算

在公式（11）中，当t＝ta，exp（－t/ta）＝e－1.因此，ta作为一特征时间尺度，表明了R≈r，即主震造成的余震时间序列随时间的衰减已接近于背景场（主震前）的地震活动性.由此，通过对余震背景场的区别，我们可以很容易地确定余震的持续时间.但是一个确定的转折点却是很难或者几乎不能确定的.虽然我们无法判断余震和背景场地震转折的具体时间，但余震持续时间的上下界还是能够基本确定的.事实上，公式（11）给出的即是余震持续时间的下界.

3.1 对数线性回归计算

图5 唐山地震余震数据对数线性拟合

首先，分别取唐山地震后MS≥2.0和MS≥3.0的余震序列，计算该区域的地震年发生率随时间的变化，并对其进行对数线性拟合.当地震年发生率回到该区域地震背景场时，则认为余震不再持续.从地震发生到余震年发生率回到背景场的这段时间即为余震持续时间ta（Toda et al，1998）.为了更好地对比，增加结果的可信度，此处在计算背景场地震次数时，我们分别应用了：①公元1000—1976年MS≥4.0的地震目录，由G－R定律分别计算MS≥2.0和MS≥3.0时的背景场地震次数；②1970—1976年MS≥2.0的地震目录（图5a，b）.考虑到1970—1976年MS≥2.0的地震记录有较多遗漏，图5a中由该背景场得到的余震持续时间显然偏大.由于震后短时间内记录小震的缺失，图5a，b中大震发生后的2—3天内，实际地震数据小于拟合直线.由于对小震的监测能力随时间的增强，图5a中拟合直线斜率的绝对值小于图5b中拟合直线的绝对值，而由于地震记录中小震的缺失，则图5a中直线截距会偏小.对比图5a，b，由有感地震背景场为参考得到的余震持续时间，当MS≥2.0时的结果仅略小于MS≥3.0时得到的余震持续时间.因此虽然监测能力随时间增强会造成余震持续时间的高估，而小震缺失则会导致余震持续时间的低估.但综合考虑二者，其不确定性对结果的影响并不明显.而由于公元1000年到唐山地震前有感地震可能有较多的遗漏，以有感地震目录为背景场时，也会高估余震的持续时间.综上所述，对数线性回归计算得到的唐山地震余震持续时间，因参照了图5b中，以1970—1976年MS≥3.0的地震为背景场时得到的结果，故唐山地震余震持续时间为80 a左右.

3.2 理论计算

由公式（12），如果摩擦本构关系（公式（1））的A和B已知，且作用于断层面上的正应力和远场剪应力加载速率已知，就可以估算余震序列的持续时间ta.实验结果表明，A的取值范围为0.005—0.010（Dieterich，1992）.从公式（12）中可得知，如果A＝0，即断层摩擦过程与滑移速率无关，则ta＝0，余震与主震同时发生，显然有悖实际观测现象.对于σn的取值存在较大的区间范围，Harris和Simpson（1998）对加州San Andras Fault的研究给出σn＝30 MPa，而在5—15km深度的静水流体压力则给出σn＝18 MPa（Beeler，2004）.因此Aσ的取值存在较大的变化范围.本文中，我们采用Aσ＝1.0×105Pa.这一结果来自于Belardinelli等（1999）的计算结果（Aσ≈8.0×105—9.0×105Pa）.这一结果与前人工作（Dieterich，1994；Gross，Kisslinger，1997；Gross，Bürgmann，1998；Harris，Simpson，1998）是一致的.剪应力的加载变化率˙τ无法直接测得，下面讨论几种不同方法求取˙τ从而得到ta.

1）根据剪应力变化率与静态应力降Δτe及地震回复周期tr之间的近似关系（Dieterich，1994）

式中，Δτe为主震静态应力降.运用诺波夫走滑断层模型中静态应力降和断层宽度、平均滑动位移的关系（Knopoff，1958），有

式中，W为唐山地震断裂的断层宽度，D为唐山大地震的平均滑动位移，μ为剪切模量.取断层宽度为20km（Huang，Yeh，1997；HarvardcmT网①http：∥www.globalcmt.org/CMTsearch.html），平均滑动位移为3.53 m（Huang，Yeh，1997），剪切模量μ＝3×1010Pa，由公式（14）得Δτe＝33.7×105Pa.华北东部地区断层的复发周期为3 000—7 000 a（邓起东等，1994），而最近研究表明此处的复发周期被进一步降低（王绳祖，张宗淳，2001），代入公式（13），此处取复发周期为3 000 a，则可得到˙τ约为1×103Pa/a.由公式（12）即可求得余震持续时间为100 a左右.

关于地震回复周期Tr的估算，来源于前人的研究（邓起东等，1994）.不过近期的研究表明，如果我们已知宏观地震矩M0和研究区域内的˙δ0，即远场加载速率，那么区域内唐山地震发震断层的复发周期Tr可估算为（Chen et al，2007）

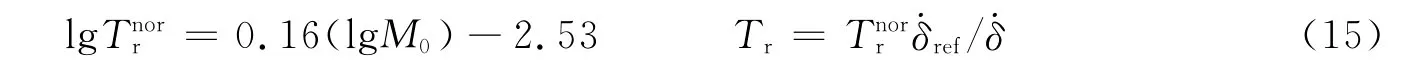
式中，Tnorr为以加州San Andras fault正规化的回复周期（单位：a），M0为地震矩（单位：10－7N·m），˙δref＝2.3cm/a为参考加载速率，˙δ为断层加载速率.此方法求得的回复周期约为2 000 a，代入公式（12）和（13），则余震持续时间为70 a.如果考虑到公式（15）回归计算时的标准方差平均回复周期存在的不确定性，则余震持续时间可达100 a.

2）由于远场剪应力加载速率˙τ的准确求取存在较大的不确定性，Dieterich（1994）采用了剪应力加载速率和地震回复周期Tr，主震静态应力降Δτe.得到˙τ≈Δτe/tr.由此ta≈trAσ/Δτe.其问题在于Tr给出的地震发生的平均回复周期Δτe为一常数量，即Δτe不依赖于地震震级的大小，因此ta实际上正比于地震的回复周期.我们也知道，大震的回复周期远大于中小地震的回复周期，这一点从G－R关系可知.因此，ta～Tr隐含了随着震级的下降，余震的持续时间也是减小的.然而实际的地震观测显示，余震持续时间与地震震级的关系并不明确.因此，Ziv和Rubin（2003）给出了修正公式式中，˙δ0为远场加载速率，W为断层宽度，μ为断层面上的剪切模量.并且Ziv和Rubin（2003）通过对加州若干地震的研究证实，震级的减小并未造成余震持续时间的明显减小.取剪切模量μ＝3×1010Pa，背景场速率在断层走向方向上投影˙δ＝0.08cm/a（Wang et al，2001；Shen et al，2000），唐山地震断层宽度W＝20km（Huang，Yeh，1997；HarvardcmT网①http：∥www.globalcmt.org/CMTsearch.html）.由公式（16）可求得˙τ＝1 200 Pa/a，代入公式（12）得到余震的持续时间ta＝84 a.

3）实际上，远场剪应力速率˙τ也可以由背景场的地震活动性求取，即背景场地震活动性R0可以反映区域的剪应力加载速率.根据圆盘断层模型：M0＝16ΔσsR3/7及相应的地震矩变化率，Console等（2006）给出

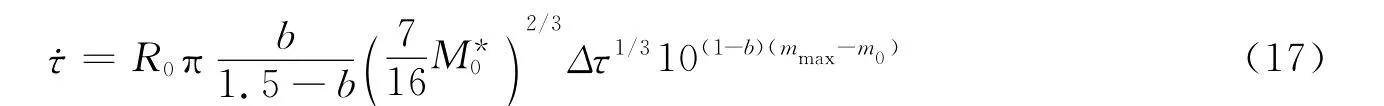
式中，单位面积内地震年发生率R0＝N0/ΔtStot，N0为Δt时间内的地震次数，Stot为区域面积.是震级为m0的地震的地震矩，M0为已知的震级为m的地震的地震矩（Console et al，2006）.对背景场地震活动性分布进行空间光滑后，得到二维的余震持续时间如图6，可以看到区域内的余震持续时间大多为130—160 a.图6为由地震背景场计算得到的唐山断层所在区域的余震持续时间.

4 结果对比

表1为本文所用4种方法计算所得的唐山大地震余震持续时间.上述方法得到的地震复发周期大多为100a左右.在对余震序列的对数线性回归（Toda et al，1998）计算余震持续时间ta时，其不确定性在于：①运用有感地震得到的背景场取不同震级时，余震持续时间变化不大，但由于有感地震的目录的不完备性，所得到的余震持续时间会偏大；②由于是对数线性拟合，背景场或是拟合直线微小的变化就会造成ta很大的变化.理论计算余震持续时间：方法一（Dieterich，1994）.余震持续时间的主要影响因素在于断层回复周期和主震的静态应力降，而主震静态应力降又由断层宽度和平均滑动位移决定；方法二（Ziv，Rubin，2003）.余震持续时间的主要影响因素在于断层面上的GPS形变速率和断层宽度；方法三（Console et al，2006）.由于历史地震目录可能不完整造成R0偏小，因此由公式（17）算得的剪应力变化速率˙τ偏小，进而导致余震持续时间ta偏大.另外b值的变化也会导致ta发生变化，对的计算依赖于历史地震的震级和地震矩，Mmax则是该区域历史最大地震，因而用这种方法估计余震持续时间，在历史地震目录不完整，或是地震复发周期较长、历史地震较少的区域，会有较大的误差.

图6 由地震背景场计算得到的唐山MS7.8地震断层所在区域的余震持续时间

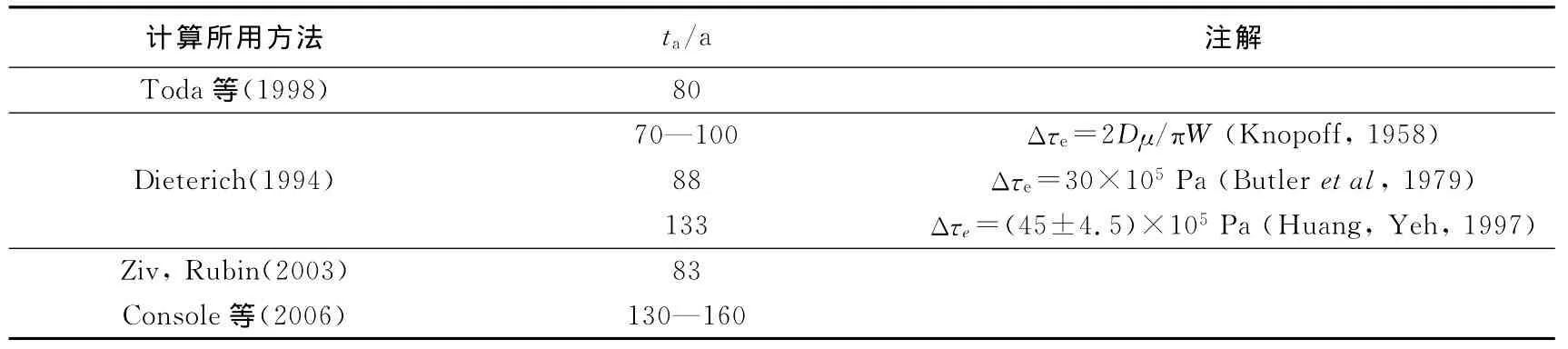
表1 唐山大地震余震持续时间Table 1 Duration of aftershock sequences in Tangshan region

对比Stein和Liu（2009）在对内陆地震余震序列的研究中给出的余震持续时间与断层加载速率的关系，唐山地震的余震持续时间亦为100 a左右.

5 讨论与结论

如果假设震前与震后的远场剪应力加载速率一致，那么余震随时间的发生率公式（11）可写为

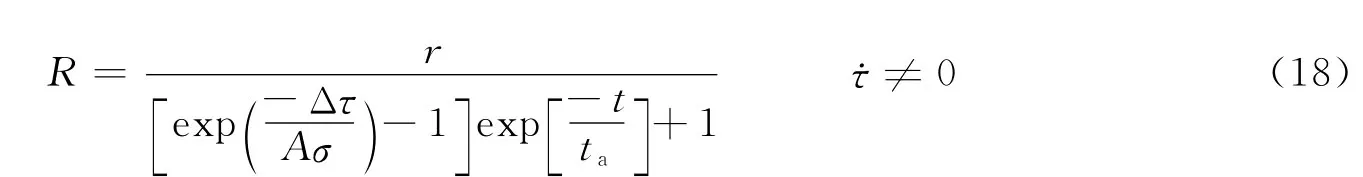
式中，Δτ取唐山地震主震最大库仑应力变化2×105Pa（Robinson，Zhou，2005；万永革等，2008），余震持续时间ta取85 a，那么由上述公式给出的年发生率随时间的衰减如图7实线所示.图中方块为由实际地震数据求取的地震年发生率.在地震刚发生的一年之内，拟合的数据与实际地震数据有区别，其原因可能有：①地震刚发生时˙τ不能简单地近似成˙τr；②地震刚发生时的应力变化远大于主震最大库仑应力变化（Helmstetter，Shaw，2009），这便导致了地震次数的显著提高.而主震发生一年之后实际地震数据就与由背景场计算得到的地震年发生率R较为吻合.图7为唐山地震后由地震目录得到的实际地震年发生率及根据公式（18）由背景场计算得到的地震年发生率.

图7 1976年唐山MS7.8地震后余震年发生率随时间的变化.图中方块为由实际地震数据求得到的MS≥2.0地震年发生率.虚线、实线和点划线均为应用公式（18）由背景场地震计算得到的MS≥2.0地震年发生率.计算中，取Aσ＝1，ta＝85 a，虚线、实线和点划线分别对应Δτ＝0.4，0.2，0.1 MPaFig.7 Theoretical estimation of annual number of the aftershocks engendered by 1976 MS7.8 Tangshan earthquake.Squares mark annual number of MS≥2.0 aftershocks calculated after the earthquake catalogue.Dashed，solid and dash－dot lines all denote annual rate of MS≥2.0 earthquakes calculated after the formula（18）.In calculation we assumed Aσ＝1 and ta＝85 yrs.Dashed，solid and dash－dot lines give the curves withΔτ＝0.4，0.2 and 0.1 MPa，respectively

Stein和Liu（2009）指出，要想使得地震危险性评估进一步提高，需要将断层体系作为一个复杂的系统，并提出运用古地震的研究以及GPS观测方法来研究地震活动性，从而到达判断区域内地震活动性是否是以前大地震的余震以及能否预测未来的大地震.

基于Dieterich（1994）的余震触发机制，我们从不同角度讨论了余震的持续时间，理论计算和数据拟合结果表明，1976年唐山地震的持续时间可达百年.虽然计算中的不确定性因素仍然存在，但结果反映了大陆内部地震序列与板缘地震的明显差异，断层长时间的演化如果如滑动速率－滑动状态摩擦准则所描述，余震的持续时间则反映了从加速至瞬态失稳的特征时间尺度.因此，正确地认识地震序列，对于地震的触发机制的研究有着重要的意义.地震的触发机制的研究则可应用于基于时间的地震危险评价.因为对于一些属于某些大地震所触发的小震来说，将其作为未来大地震发生的地点会存在一些问题，而将这些小震全部去除则又可能降低了该区域地震危险性，因此如何保留强余震仍是需要深入研究的问题.由于地震活动时空上的多样性以及大地震有着较长的余震持续时间，尤其对于大陆地震而言，这些问题会导致大陆内部地震危险性的评估变得十分困难.短时期来说，因为一些余震的危险性，我们不能放弃对地震危险性的评价；长期来讲，仅仅依赖于现在的地震活动性，有可能是上次地震后所触发的余震，从而可能会高估这一地区的地震危险性，而低估了另一些地区的地震危险性.

邓起东，徐锡伟，于贵华.1994.中国大陆活动断裂的分区特征及其成因［G］∥中国活动断层研究.北京：地震出版社：1－－14.

万永革，沈正康，刁桂苓，王福昌，胡新亮，盛书中.2008.利用小震分布和区域应力场确定大震断层面参数方法及其在唐山地震序列中的应用［J］.地球物理学报，51（3）：793－－804.

尤惠川，徐锡伟，吴建平，何正勤.2002.唐山地震深浅构造关系研究［J］.地震地质，24（4）：571－－582.

王绳祖，张宗淳.2001.地震时空影响域、复发间隔和有效孕震时间［J］.中国地震，17（4）：364－－377.

Beeler N M.2004.Review of the physical basis of laboratory－derived relations for brittle failure and their implications for earthquake occurrence and earthquake nucleation［J］.Pure Appl Geophys，161（9－－10）：1853－－1876.

Belardinelli M E，Cocco M，Coutant O，Cotton F.1999.Redistribution of dynamic stress during coseismic ruptures：Evidence for fault interaction and earthquake triggering［J］.J Geophys Res，104（B7）：14925－－14945.

Butler R，Stewart G S，Kanamori H.1979.The July 27，1976 Tangshan，China earthquake：A complex sequence of intraplate events［J］.Bull Seism Soc Amer，69（1）：207－－220.

Chen K H，Nadeau R M，Rau R.2007.Towards a universal rule on the recurrence interval scaling of repeating earthquakes？［J］.Geophys Res Lett，34（16）：L16308，doi：10.1029/2007GL030554.

Console R，Murru M，Catalli F.2006.Physical and stochastic models of earthquake clustering［J］.Tectonophysics，417（1）：141－－153.

Cornell C A.1968.Engineering seismic risk analysis［J］.Bull Seism Soc Amer，58（5）：1583－－1606.

Dieterich J H.1979.Modeling of rock friction 2.Simulation of preseismic slip［J］.J Geophys Res，84（B5）：2169－－2175.Dieterich J H.1981.Constitutive properties of faults with simulated gouge［J］.Mechanical Behavior of Crustal Rocks，24：103－－120.

Dieterich J H.1992.Earthquake nucleation on faults with rate and state－dependent strength［J］.Tectonophysics，211（1－－4）：115－－134.

Dieterich J H.1994.A constitutive law for rate of earthquake production and its application to earthquake clustering［J］.J Geophys Res，99（B2）：2601－－2618.

Gomberg J，Beeler N M，Blanpied M L，Bodin P.1998.Earthquake triggering by transient and static deformations［J］.J Geophys Res，103（B10）：24411－－24426.

Gross S，Bürgmann R.1998.Rate and state of background stress estimated from the aftershocks of the 1989 Loma Prieta，California，earthquake［J］.J Geophys Res，103（B3）：4915－－4927.

Gross S，Kisslinger C.1997.Estimating tectonic stress rate and state with Landers aftershocks［J］.J Geophys Res，102（B4）：7603－－7612.

Harris R A，Simpson R W.1998.Suppression of large earthquakes by stress shadows：A comparison of Coulomb and rate－and－state failure［J］.J Geophys Res，103（24）：439－－451.

Helmstetter A，Shaw B E.2009.Afterslip and aftershocks in the rate－and－state friction law［J］.J Geophys Res，114：B01308.doi：10.1029/2007JB005077.

Huang B，Yeh Y T.1997.The fault ruptures of the 1976 Tangshan earthquake sequence inferred from coseismic crustal deformation［J］.Bull Seism Soc Amer，87（4）：1046－－1057.

King G C P，Stein R S，Lin J.1994.Static stress changes and the triggering of earthquakes［J］.Bull Seism Soc Amer，84（3）：935－－953.

Knopoff L.1958.Energy release in earthquakes［J］.Geophys J，1（1）：44－－52.

Kramer S L.1996.Geotechnical Earthquake Engineering［M］.Singapore：Pearson Education Inc：106－－138.

Marone C.1998.Laboratory－derived friction laws and their application to seismic faulting［J］.Ann Rev Earth Planet Sci，26（1）：643－－696.

Parsons T，Velasco A A.2009.On near－source earthquake triggering［J］.J Geophys Res，114：B10307.doi：10.1029/2008JB006277，doi：10.1029/2008JB006277.

Rice J R，Gu J C.1983.Earthquake aftereffects and triggered seismic phenomena［J］.Pure Appl Geophys，121（2）：187－－219.

Robinson R，Zhou S.2005.Stress interactions within the Tangshan，China，earthquake sequence of 1976［J］.Bull Seism Soc Amer，95（6）：2501－－2505.

Ruina A.1983.Slip instability and state variable friction laws［J］.J Geophys Res，88（10）：359－－370.

Scholz C H.1998.Earthquakes and friction laws［J］.Nature，391：37－－42.

Shen Z，Zhao C，Yin A，Li Y，Jackson D D，Fang P，Dong D.2000.Contemporary crustal deformation in east Asia constrained by Global Positioning System Measurements［J］.J Geophys Res，105（B3）：5721－－5734.

Stein S，Liu M.2009.Long aftershock sequences within continents and implications for earthquake hazard assessment［J］.Nature，462（5）：87－－89.

Toda S，Stein R S，Reasenberga P A，Dieterich J H，Yoshida A.1998.Stress transferred by the 1995 MW＝6.9 Kobe，Japan，shock：Effect on aftershocks and future earthquake probabilities［J］.J Geophys Res，103（24）：543－－565.

Wang Q，Zhang P Z，Freymueller J T，Bilham R，Larson K M，Lai X，You X，Niu Z J，Wu J C，Li Y X，Liu J N，Yang Z Q，Chen Q Z.2001.Present－day crustal deformation in China constrained by Global Positioning System Measurements［J］.Science，294（5542）：574－－577.

Ziv A，Rubin A M.2003.Implications of rate－and－state friction for properties of aftershock sequence：Quasi－static inherently discrete simulations［J］.J Geophys Res，108（B1）：2051.

Aftershock duration of the 1976 MS7.8 Tangshan earthquake and implication for seismic hazard estimation

Zhong Qiu Shi Baoping
（College of Earth Science，Graduate University of Chinese Academy of Sciences，Beijing 100049，China）

10.3969/j.issn.0253－3782.2012.04.007

P315.75

A

中国科学院知识创新工程（KZCX2－YW－Q08－2）资助.

2011－06－07收到初稿，2012－03－08决定采用修改稿.

e－mail：zhongqiu09＠mails.gucas.ac.cn

仲秋，史保平.2012.1976年唐山MS7.8地震余震序列持续时间及对地震危险性分析的意义.地震学报，34（4）：494－－508.

Zhong Qiu，Shi Baoping.2012.Aftershock duration of the 1976 MS7.8 Tangshan earthquake and implication for seismic hazard estimation.Acta Seismologica Sinica，34（4）：494－－508.