地壳应变场观测中体应变与面应变转换系数的计算＊

张凌空牛安福吴利军

1）中国北京100045中国地震台网中心

2）中国北京100036中国地震局地震预测研究所

地壳应变场观测中体应变与面应变转换系数的计算＊

张凌空1），牛安福1）吴利军2）

1）中国北京100045中国地震台网中心

2）中国北京100036中国地震局地震预测研究所

将钻孔体应变仪与分量式应变仪的观测资料在面应变平台上进行整合，对于解决目前两种应变仪观测数据的评估、分析、处理和地震预报问题有实际意义.根据潘立宙－陈沅俊和Evertson理论及弹性力学知识，分别建立了平面应力作用下体应变和面应变观测的力学模型，推导了观测钻孔、空孔和无孔岩石体应变与面应变转换系数的计算公式，发现它们都可以归结为同一公式描述，差异仅在于k（体应变仪钢筒内壁或无孔岩石面应变与空孔岩石面应变之比）的取值不同.用Evertson理论推导的公式与空孔岩石情形相近，当岩石弹性模量为4 ×1010—8×1010Pa时，二者都可以看成是对潘－陈公式的一种简化、近似计算；无孔岩石的情况则相当于在岩石弹性模量为1×1010Pa时对该式的一种估计.文中结合实际情况对转换系数的各种影响因素进行了详细分析.

体应变 面应变 转换系数 弹性模量 泊松系数

Abstract：This study aims at integrating the observational data recorded by borehole volume strainmeters and component borehole strainmeters on the area strain basis.This is helpful for current data evaluation，data processing and analysis，and earthquake prediction.Based on the Pan－Chen model（Pan；Chen and Yang），Evertson theory and theory of elasticity，both volume strain and area strain models were set up under area stress.In addition，we have derived similar formulas for calculating transform coefficient between volume strain and area strain in observation hole，empty hole and non－porous rock condition，respectively.The difference only lies in the factor k（ratio of volume strain gauge on the steel cylinder wall or non－porous rock surface strain to area strain of the empty hole rock）.The theoretical formula derived from Evertson model is close to the case of empty hole rock with the rock elastic modulus ranged from 4×1010Pa to 8×1010Pa.Both results may be regarded as a simplified Pan－Chen model.For non－porous rock，the factor k may be predicted by taking rock modulus as 1×1010Pa.This paper discussed some factors related to transform coefficient based on real observation data.

Key words：volume strain；area strain；transform coefficient；elastic modulus；Poisson coefficient

引言

钻孔应变仪具有观测精度高、响应频带宽和产出数据质量好等突出优点，现已成为国际上地壳应变场观测的主流仪器.该种仪器分为两大类：一类是体应变仪，另一类是分量式应变仪.“十五”期间受美国“板块边界观测计划（PBO）”的激励（张宝红，2004，2010），中国地震局进行了大规模数字化地震观测网络建设，钻孔应变仪作为重要的形变前兆观测仪器开始了大发展时期，从2007年起陆续在全国许多台站投入使用.据中国地震台网中心前兆数据库统计，TJ－2型体应变仪建立了80个测点，YRY－4型和RZB型分量式应变仪分别建立了40个和12个测点，主要分布在首都圈、山西地震带、东南沿海和南北地震带等重要地震监测区，目前台点还在不断增加.如果根据有关数理模型（潘立宙，1981；陈沅俊，杨修信，1990），将体应变观测数据转换成面应变，分量式应变仪经过两组相互垂直的测项加组合和校正（邱泽华等，2005a）也换算成面应变，就可以将这两种应变仪测得的岩石面应变进行比较，这对解决钻孔应变仪观测数据的评估、分析、处理和地震预报问题有实际意义.目前，将体应变转换成面应变的工作在国内外还基本是个空白，主要原因是以前使用的分量式应变仪比较少，中国大陆大约有8套，美、日两国大约分别有4套和8套，因而当时开展这项研究工作没有太大的实用价值.有关学者（苏恺之等，2003；邱泽华，石耀霖，2004；邱泽华，2010；欧阳祖熙等，2009；牛安福等，2011）对国内外钻孔应变仪的发展状况已分别进行了系统的总结和阐述.近些年随着分量式应变仪在中、美两国的大量布设，体应变与面应变的转换问题随之提到议事日程，尤其是2008年汶川地震以后，如何将体应变观测资料在地震监测、预报中更加合理、有效地使用就愈发显得重要和紧迫.

1 观测井和仪器概况

目前，我国使用的钻孔体应变仪分为两种：一种是20世纪80年代中期从美国引进的Sacks－Evertson型（Sacks，Evertson，1971；刘澜波等，1986），应变灵敏度可达1×10－11，井孔深度在250—400 m；另一种是国产TJ型，“九五”以后大量使用的是TJ－2型，它是在Sacks－Evertson型基础上加以改进的产品（苏恺之等，2003），其应变灵敏度达0.5×10－9，钻孔深度一般在60—100 m.两种探头与井下岩石耦合均采用膨胀水泥固结方式，当岩石对仪器钢筒产生挤压作用时，筒内硅油的压力会发生改变，通过波纹管或液压传感器的微小位移可测得体应变变化.

2 钻孔应变观测力学模型的建立

2.1 基于潘－陈理论建立的力学模型

设有一块无限大的岩石平板，该平板在无穷远处承受两项均匀拉应力（σ1，σ2），平板中有一半径为r3的井孔，安置其中的体应变仪钢筒内半径为r1，外半径为r2，中间通过膨胀水泥与岩石耦合，因而钻孔的实际情况为双衬套结构.设钢筒、水泥、岩石的弹性模量和泊松比分别为E1，ν1，E2，ν2，E3，ν3.假定钻孔所处介质近似为各向同性弹性体，遵从虎克定律，且井口及井底对传感器的影响可以忽略，钻孔的轴向应力为0.在这种条件下，陈沅俊和杨修信（1990）根据潘立宙（1981）的工作进一步推导出钢筒内壁上的面应变为

M1是与各层材料的弹性参数及半径有关的一个常数，称为测量系统的特征系数，其值为

x4由下列四元一次线性方程组确定

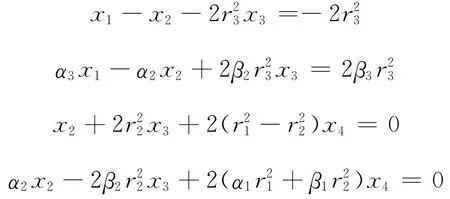
其中系数为

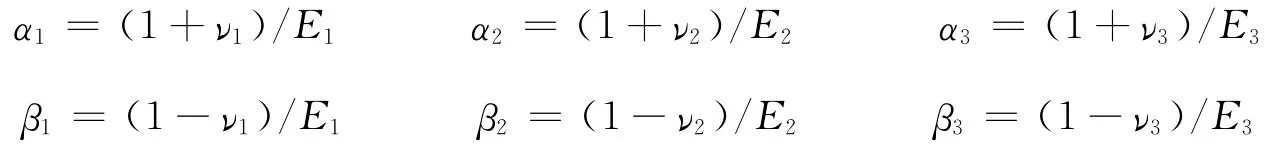
解得

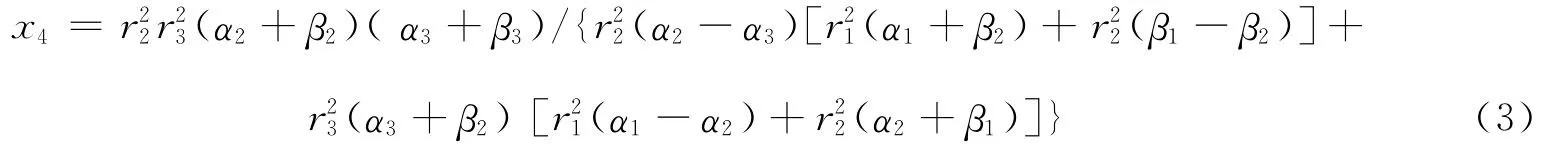
将式（2）代入式（1），得

考虑到钢筒、水泥和岩孔耦合的边界条件，并忽略钢筒形状和尺寸等因素的影响，可以认为钢筒沿其轴向的相对变化量近似等于其周围岩体的轴向应变，即

则钻孔体应变仪测得的体应变为

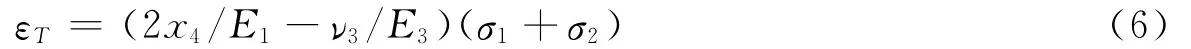
又知，在平面应力作用下，空孔岩石的径向位移为（王仁，1979）

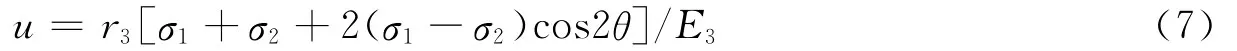
θ为任意方向孔径与最大主应力之间的夹角，求得的径向应变为

因为面应变等于任意两组相互垂直的线应变之和（θ，θ＋90°），所以空孔岩石的面应变为

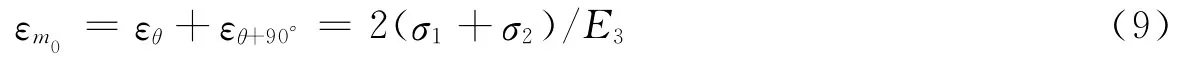
于是

该式表明k的物理含义是钢筒内壁面应变与空孔岩石面应变之比.略作变换，有

将式（11）分别代入式（6）和式（10）

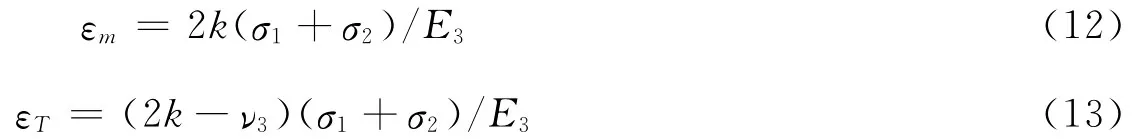
式（12）、式（13）就是在平面应力作用下，基于潘－陈理论建立的钻孔面应变和体应变观测的力学模型.

2.2 基于Evertson理论建立的力学模型

美国Sacks－Evertson体应变仪研制者之一Evertson（1977）总结出，在三向空间应力σ1，σ2，σ3作用下，探头钢筒内壁上的体应变可以写成

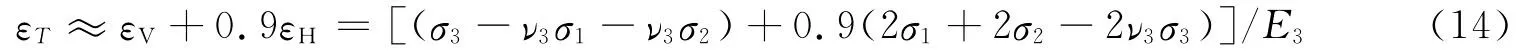
式中，εV，εH分别是空孔垂直应变和面应变，0.9是平面应力作用下钢筒内壁面应变（εm）与空孔岩石面应变（εm0）之比（精确值为0.87195），也就是前面所说的k值（k＝εm/εm0）.如果0.9用k表示，则式（14）可以改写成

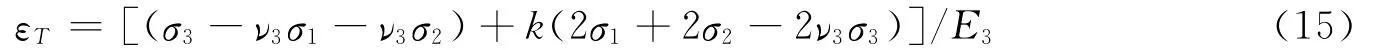
在平面应力作用下（σ3＝0），式（15）变为

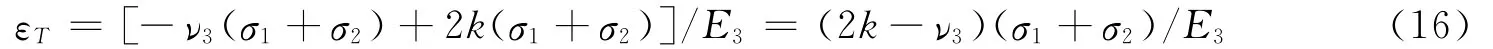
其面应变为

式（16）、式（17）就是基于Evertson理论建立的钻孔体应变和面应变观测的力学模型.

2.3 两组模型的比较

基于两种理论建立的面应变和体应变的力学模型表述形式完全一样，差异仅在于k的取值不同.一个是由潘－陈理论推导出的比较复杂的函数关系式k＝（x4E3）/E1；另一个是Evertson根据拉梅厚壁圆筒方程得出的常数0.87195，比较的焦点在于哪个k值更符合实际情况.将Sacks体应变井有关参数（E1＝19.6×1010Pa，ν1＝0.3；E2＝2×1010Pa，ν2＝0.35；r1＝54mm，r2＝57mm，r3＝76mm）代入k式，则k只与岩石弹性参数有关.图1显示k值并非常量，当E3不变时k与ν3近似呈线性关系，随其增加而减小；当ν3不变时，k随E3增加而增大；当E3＝1×1010—3×1010Pa时，k随E3增加快速上升，幅度达到0.3525，之后速率逐渐减小，各条曲线相互靠近.Evertson理论假定，钢的弹性模量（E1）是岩石（E3）的3倍（E1＝3E3），并且两者的泊松系数（ν1＝ν3）相等.事实上，E1＝19.6× 1010Pa，ν1＝0.3，E3＝1×1010—8×1010Pa，ν3＝0.20—0.35，假设条件不是严格成立，尤其是E3波动范围较大，因此模型只是通常情况下的平均估计，0.87195近似等于由图1得到的平均k值（0.8453）.当岩石较软，即E3＝1×1010—3×1010Pa时，两数值明显偏离很多.潘－陈模型考虑了各种因素对k值的影响，理论公式推导比较严格，不存在此类假设问题，从这个角度分析，潘－陈模型应更为合理.

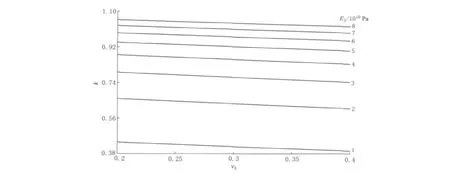
图1 钢筒内壁面应变和空孔岩石面应变之比（k）与岩石弹性参数（E3，ν3）的关系Fig.1 Relation between the ratio of steel tube wall plane strain to strain outside a borehole in an infinite rock plate（k）and the rock elastic parameters（E3，ν3）

3 钻孔体应变与面应变转换系数的计算

根据式（12）、（13）或式（16）、（17），可以得到

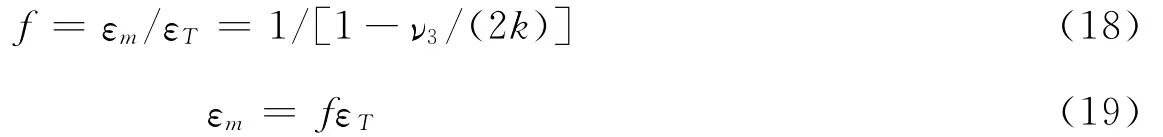
式中，f是钻孔体应变与面应变的转换系数，利用这一关系可以将体应变测量值换算成面应变，从而可与分量式应变仪测得的面应变进行比较.

当k＝（x4E3）/E1时，就是基于潘－陈力学模型下的体应变与面应变的转换系数

当k＝0.9时，就是基于Evertson力学模型下的体应变与面应变的转换系数

将Sacks井有关参数代入式（20），以ν3为自变量、f1为因变量作曲线（图2a），可知f1随ν3增加而增大.当E3＝4×1010—8×1010Pa时，f1各条曲线近于重合；而由式（21）算得的f2曲线（虚线）也恰恰分布于这一区域，说明f2是f1的一种特殊情况.通常岩石的E3在4×1010—8×1010Pa，ν3在0.20—0.35，这时k值接近0.87195，f2≈f1，所以一般情况下f2可以取代f1，并且计算简单，只涉及一个参数.但当岩石较软、易于发生弹性变形时，即E3＜3×1010Pa，f2与f1误差较大.国产体应变仪研制者苏恺之等（2003）给出了TJ－2型体应变观测井的有关参数，E1＝21×1010Pa，ν1＝0.3；E2＝3×1010Pa，ν2＝0.25；r1＝42mm，r2＝44.5mm，r3＝65mm，将这些参数代入式（20），同样可以做出类似图2a的曲线（图2b），只是k值略小、f1值略大.

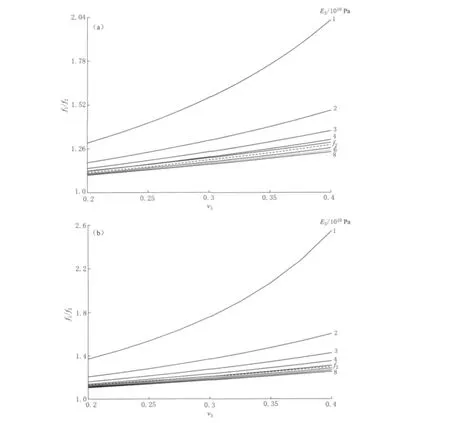
图2 两种体应变仪的f1与f2（图中4与8之间的虚线）比较（a）Sacks－Evertson型；（b）TJ－2型Fig.2 Comparison between f1and f2（dashed line in two figures）for two kinds of borehole volume strainmeters（a）Sacks－Evertson type；（b）TJ－2 type

根据宝坻等台岩石弹性参数实际测定结果，分别对各台站f1和f2进行计算（表1）.昌平台k值明显偏小，导致f1大于f2，E3过小是造成这种差距的主要原因；其余6个台站k值与0.87195比较接近，因而求得的f2值与f1误差较小.

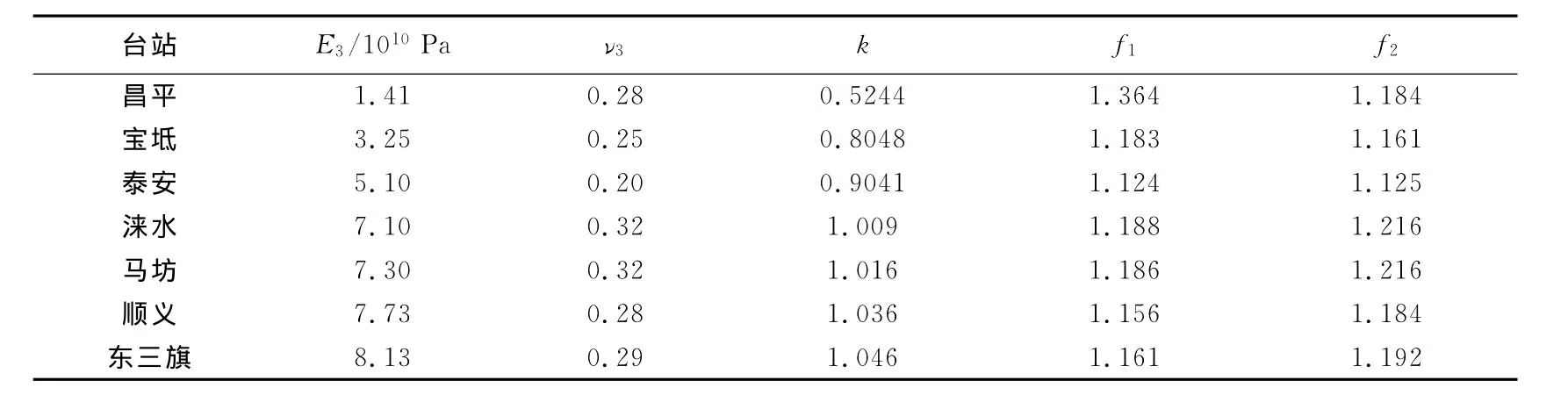
表1 用两个公式计算的实际台站体应变与面应变转换系数的对比Table 1 Comparison between conversion factors from volume to area strain estimated by two formulas for several stations

4 钻孔体应变与面应变转换系数的影响因素分析

4.1 与岩石弹性参数的关系

图2b表明f1随ν3的增加而增大，随E3的增加而减小，说明岩石的刚度越小、横向变形越大，体应变与面应变的转换系数越大；当E3＝1×1010—2×1010Pa时，f1随ν3的增加上升速率很快，之后速率迅速减小；当E3＝4×1010—8×1010Pa时，f1各曲线接近线性，且近于重合.一般实测钻孔岩石E3＝4×1010—8×1010Pa，ν3＝0.25—0.32，则f1＝1.138—1.226，f2＝1.167—1.224，平均值f1＝1.182，f2＝1.195.

4.2 与膨胀水泥弹性参数的关系

假定岩石的弹性参数不变，取E3＝5×1010Pa，ν3＝0.25，分析f1与E2，ν2的关系.图3表明，f1随ν2的增加而减小，随E2的增加而增大，且基本呈线性关系，即水泥刚度越大、横向变形越小，体应变与面应变的转换系数越大.一般E2＝2×1010Pa（水泥较稀）—3.5×1010Pa（水泥较硬），ν2＝0.25—0.35.水泥弹性参数发生变化时，f1＝1.167—1.157，最大改变量是0.01，说明膨胀水泥对体应变与面应变转换系数的影响不是很大.

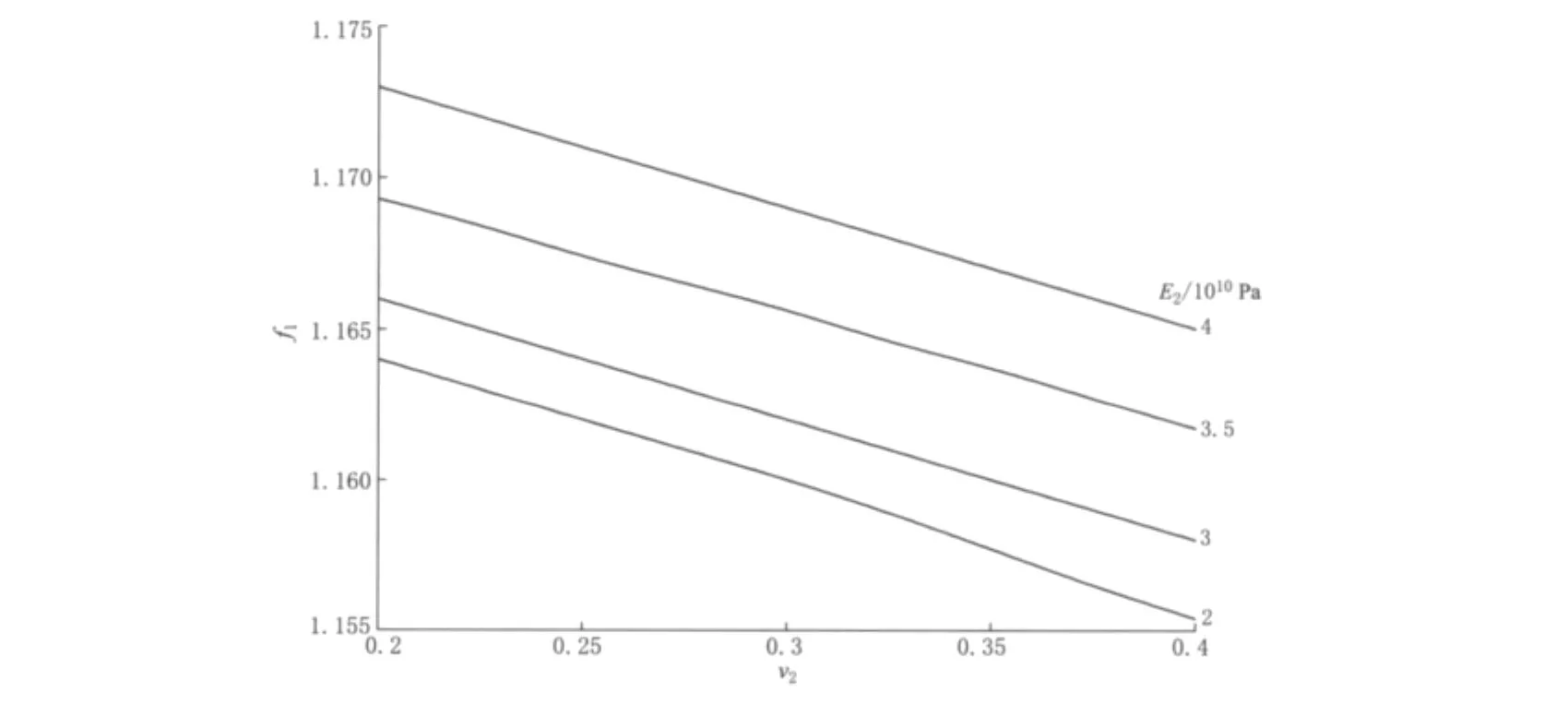
图3 转换系数（f1）与膨胀水泥弹性参数（E2，ν2）的关系Fig.3 Relation between conversion factor（f1）and elastic parameters（E2，ν2）of expanding cement

4.3 与仪器钢筒半径和钻孔孔径的关系

两代TJ型体应变仪钢筒内半径变化范围是r1＝42—54mm，外半径r2＝44—57mm，钻孔半径r3＝55—75mm，若保持n＝r2/r1＝1.060不变（苏恺之等，2003），则由式（19）可做出图4.f1与r1近似呈线性关系，随其增大而增大，在1.164—1.174之间变化；f1与r3呈非线性关系，随其增大而减小，在1.161—1.173之间变化.可见，r1和r3增减对f1最多影响0.01.

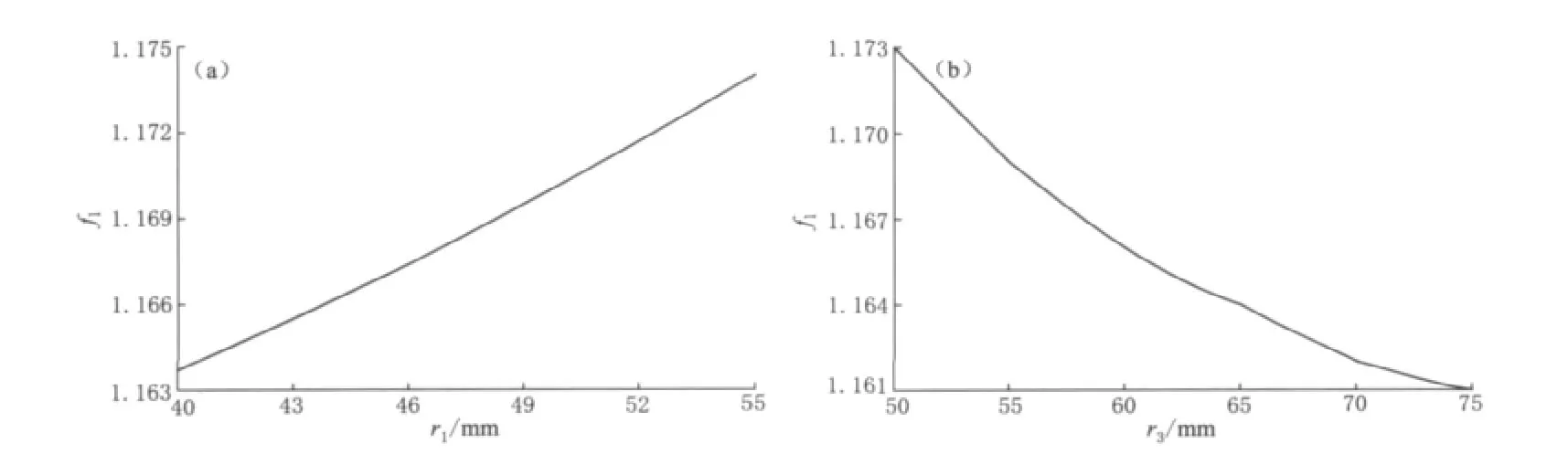
图4 转换系数（f1）与仪器钢筒半径（r1）（a）和钻孔孔径（r3）（b）的关系Fig.4 Relation between conversion factor（f1）and strainmeter steel tube radius（r1）（a）and borehole radius（r3）（b）

5 空孔岩石体应变与面应变转换系数的计算

根据式（9）可知，在平面应力作用下空孔岩石的面应变为

又根据式（5）可知，空孔岩石体应变为

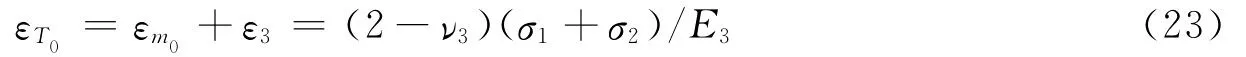
故体应变与面应变的转换系数为

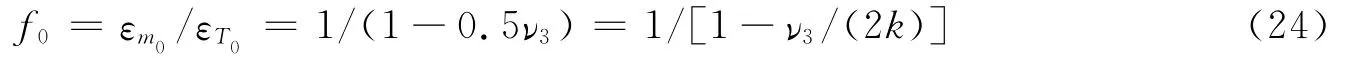
显然，f0也可以写成式（18）的形式，只是这时k＝1.

6 完整的无孔岩石体应变与面应变转换系数的计算

在平面应力作用下，无孔岩石的线应变有

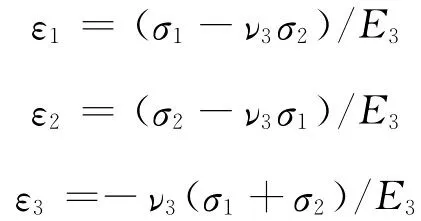
其面应变为

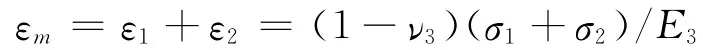
体应变为

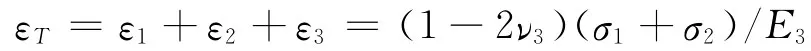
故体应变与面应变的转换系数为

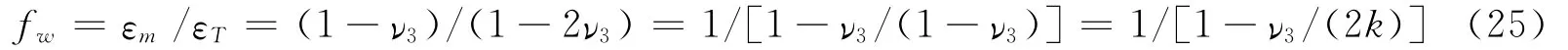
说明fw同样也可以写成式（18）形式，这时k＝（1－ν3）/2，其物理含义是岩石面应变与空孔岩石面应变之比.如果取ν3＝0.25，则fw＝1.5，故εT＝2εm/3，2/3就是由面应变固体潮理论值计算体应变固体潮理论值时常用的转换系数.

7 三组体应变与面应变转换系数之间的比较

图5显示fw与ν3呈非线性关系，随其增加而增大，并且当ν3＞0.32后速率明显加快.与图2b比较，fw曲线类似于E3＝1×1010Pa时f1的情况.当ν3＝0.2—0.32时，fw与f1近于重合，之后两曲线差距才逐渐拉大；f2与f0曲线很接近，数值平均比f0大0.032，两者都可以近似看成是E3＝4×1010—8×1010Pa时f1的特殊情况.

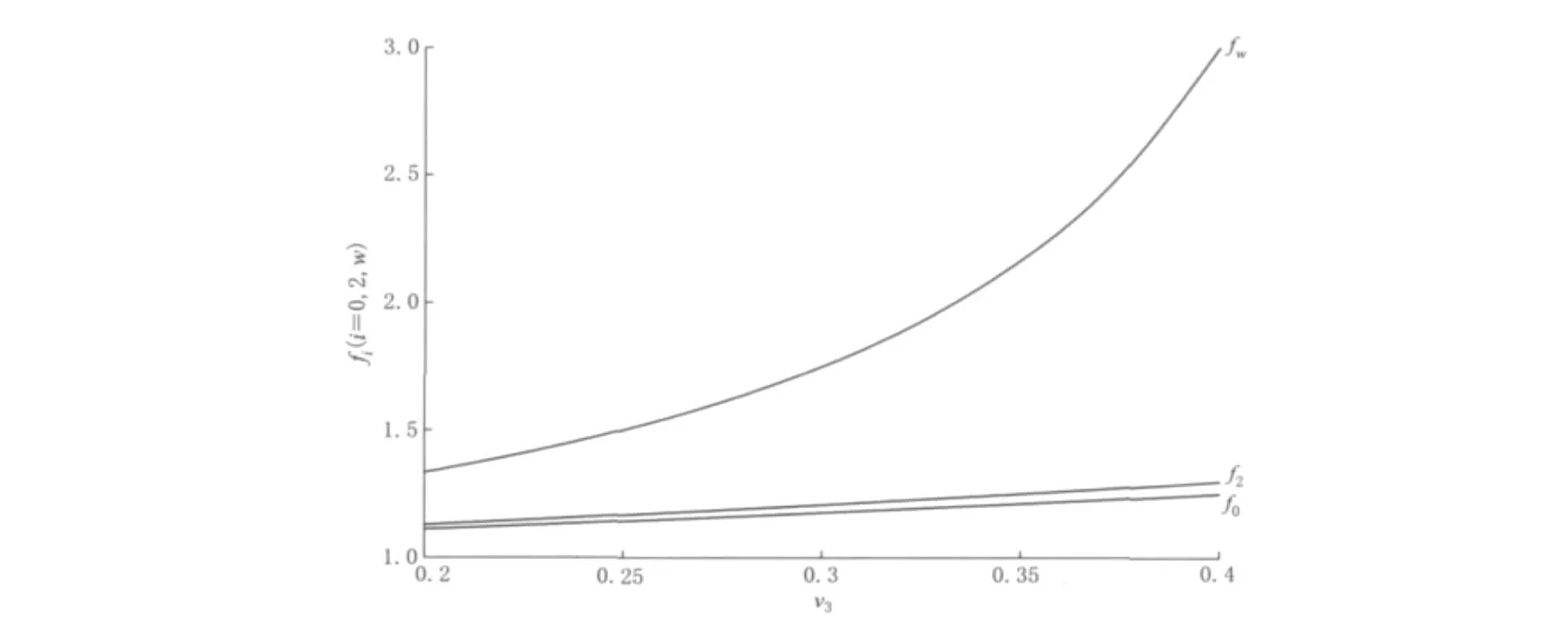
图5 三种体应变与面应变转换系数的对比Fig.5 Comparison between three conversion factors from volume to area strain in crustal strain observation

8 讨论与结论

无论是地壳观测钻孔、空孔还是无孔岩石，其体应变与面应变的转换系数都可以表述成fi＝1/［1－ν3/（2k）］的形式（i＝1，2，0，w），k的物理意义是仪器钢筒内壁面应变或无孔岩石面应变与空孔岩石面应变之比.

1）当k＝（x4E3）/E1，且观测钻孔有关参数（r1，r2，r3，E1，E2，ν1，ν2）为定值时，k只与岩石弹性模量（E3）和泊松系数（ν3）有关，为一变量，f1就是基于潘立宙－陈沅俊力学模型推导出的钻孔体应变与面应变转换系数的计算式.

2）当k＝0.87195时，f2就是基于Evertson力学模型推导出的钻孔体应变与面应变转换系数计算式.0.87195近似等于用k＝（x4E3）/E1公式计算得到的平均k值，f2相当于E3＝4×1010—8×1010Pa时f1的一种特殊情况.当E3＜3×1010Pa时f2与f1误差较大，这主要是源于“钢的弹性模量是岩石的3倍，并且二者的泊松系数相等”的假定.因此，f2不够准确、全面地反映实际情况，它是在一般情况下对f1的一种近似、简化计算.

3）当k＝1时，f0是空孔岩石体应变与面应变转换系数的计算式.f0与f2曲线很接近，但数值略小.

4）当k＝（1－ν3）/2时，fw是无孔岩石体应变与面应变转换系数的计算式.在E3＝1 ×1010Pa，ν3＝0.2—0.32时，fw与f1曲线比较接近.

5）fi公式是在平面应力作用下推导出来的，对潮汐观测研究完全适用，但当岩石平板存在垂直向应力时（如大气压）需要另作考虑.大气压对钻孔应变观测是一个不间断的长期干扰源，这是今后在进行台站数据处理时需要深入加以研究的问题，如作潮汐分析以前要首先排除日波、半日波气压的干扰.已知气压影响系数与气压周期、钻孔深度和岩石弹性参数等因素有关（张凌空等，2011），下一阶段的任务是如何以现有的气压干扰模型为基础，进一步推导在三向空间大气压力作用下体应变与面应变转换系数的计算式.美国实施PBO计划后，近年来在西部地区已安装了80多台GTSM型分量式钻孔应变仪，Roeloffs（2010）对华盛顿、俄勒冈和南加州12个台站的资料进行了分析，发现应变仪4个分量元件对气压变化的响应范围约在1.5×10－9—11.7×10－9hPa，这与中国和日本体应变仪（苏恺之等，2003；未广重二，1979）的观测结果大体一致.随着体应变仪和分量式应变仪观测资料的不断积累，中美两国今后都应加强两种应变仪面应变观测资料的比对研究，深入分析二者之间的共性和细节上的差异，并做出合理解释.

6）当仪器钢筒、膨胀水泥和钻孔的有关参数确定后，f1只与岩石弹性模量E3和泊松系数ν3有关，f1随ν3的增加而增大，随E3的增加而减小，并且在E3＜3×1010Pa时对f1影响很大；当膨胀水泥的弹性模量E2和泊松系数ν2有变化，而其它参数确定后，f1随ν2的增加而减小，随E2的增加而增大，并且对f1的最大改变量是0.01；若保持钢筒的内外半径比不变，则f1随内半径r1增大而增大，随孔径r3增大而减小，并且二者对f1最大影响量都是0.01.

7）体应变转换成面应变后还不能直接与其它台站的面应变资料进行比较（除非它们的观测条件相近），还需要求出各自的耦合系数（理论观测面应变/无孔岩石面应变＝2k/（1－ν3）），再将实测面应变除以耦合系数就得到真实的岩石面应变，这一步又称作面应变观测的实地绝对标定（邱泽华等，2005b），至此各台站之间的面应变才具有绝对的可比性.

8）井下探头附近岩石弹性参数的测定是一项非常重要的基础工作，不仅钻孔体应变与面应变的转换系数计算要用到它，而且二者的耦合系数计算也要用到它.目前除少数台站外大部分台站还没有开展这项工作，这是今后需要专项基金给与大力支持的科研项目.

邱泽华研究员和审稿专家对本文进行了认真审阅，并提出了建设性的修改意见，在此谨致诚挚谢意.

陈沅俊，杨修信.1990.双衬套钻孔应变测量的计算［J］.华北地震科学，8（4）：80－－89.

刘澜波，何世海，宁长平，刘北顺.1986.Sacks－Evertson钻孔应变仪观测网在京津地区安装［J］.中国地震，2（4）：102－－104.

牛安福，张凌空，闫伟，吉平.2011.中国钻孔应变观测能力及在地震预报中的应用［J］.大地测量与地球动力学，31（2）：48－－52.

欧阳祖熙，张钧，陈征.2009.地壳形变深井综合观测技术的新进展［J］.国际地震动态，（11）：1－－13.

潘立宙.1981.与地应力测量有关的几个公式的推导和讨论［M］∥地应力测量原理与应用.北京：地质出版社：163－－202.

邱泽华，石耀霖.2004.国外钻孔应变观测的发展现状［J］.地震学报，26（增刊）：162－－168.

邱泽华，石耀霖，欧阳祖熙.2005a.四分量钻孔应变观测的实地相对标定［J］.大地测量与地球动力学，25（1）：118－－122.

邱泽华，石耀霖，欧阳祖熙.2005b.四分量钻孔应变观测的实地绝对标定［J］.地震，25（3）：27－－34.

邱泽华.2010.中国分量钻孔地应力－应变观测发展重要事件回顾［J］.大地测量与地球动力学，30（5）：42－－47.

苏恺之，李海亮，张均，李秀环，马相波.2003.钻孔地应变观测新进展［M］.北京：地震出版社：1－－56.

王仁.1979.固体力学基础［M］.北京：地质出版社：188.

张宝红.2004.美国的板块边界观测（PBO）计划［J］.大地测量与地球动力学，24（3）：105－－108.

张宝红.2010.美国板块边界观测（PBO）中的钻孔应变观测设备［J］.大地测量与地球动力学，30（增刊Ⅰ）：40－－44.

张凌空，王广才，牛安福.2011.周期气压波对地壳应变场观测影响的若干因素分析［J］.地震学报，33（3）：351－－361.

周龙寿，邱泽华，唐磊.2008.地壳应变场对气压短周期变化的响应［J］.地球物理学进展，23（6）：1717－－1726.

未广重二.1979.地殻变動連續観測と埋入式歪計（Ⅰ）［J］.测候时报，46（1－－2）：9－－25.

Evertson D W.1977.Borehole strainmeters for seismology［R］∥Rep.ARL－TR－77－62.Applied research Lab，University of Texas，Audtin，Texas：1－－141.

Roeloffs E.2010.Tidal calibration of plate boundary observatory borehole strainmeters：Roles of vertical and shear coupling［J］.J Geophys Res，115（B06405）：25.

Sacks I S，Evertson D W.1971.Sensitive borehole strain－rate meters［M］∥Carnegie Institution，Washington Yearbook.Washington：Carnegie Institution，68：448－－453.

Conversion factors from volume to area strain in crustal strain observation

Zhang Lingkong1），Niu Anfu1）Wu Lijun2）
1）China Earthquake Networks Center，Beijing 100045，China
2）Institute of Earthquake Science，China Earthquake Administration，Beijing 100036，China

10.3969/j.issn.0253－3782.2012.04.005

P315.72＋7

A

地震行业科研专项（201108009）资助.

2011－08－24收到初稿，2011－12－23决定采用修改稿.

e－mail：zhll1023＠163.com

张凌空，牛安福，吴利军.2012.地壳应变场观测中体应变与面应变转换系数的计算.地震学报，34（4）：476－－486.

Zhang Lingkong，Niu Anfu，Wu Lijun.2012.Conversion factors from volume to area strain in crustal strain observation.Acta Seismologica Sinica，34（4）：476－－486.