核向量机算法研究及应用

许 敏

（无锡职业技术学院电子与信息技术学院，江苏 无锡 214121）

核向量机算法研究及应用

许 敏

（无锡职业技术学院电子与信息技术学院，江苏 无锡 214121）

对训练样本规模为m的标准支持向量机（Support Vector Machine，SVM）进行训练，时间复杂度为O（m3），空间复杂度为O（m2）。文章研究将其转换成等价的最小包含球（Minimum Enclosing Ball，MEB）形式，使用核心集向量机（Core Vector Machine，CVM）高效获得近似最优解。CVM的优点是时间复杂度与训练样本规模m呈线性关系，空间复杂度与m无关。实验证明，CVM可以对大规模数据集进行高效的分类。

核向量机；支持向量机；最小包含球；核函数

在各种机器学习中，核方法是最成功的算法之一，其最著名的例子就是在支持向量机中的应用。许多核方法都能转换成标准二次规划（Quadratic Programming，QP）问题。当标准样本集大小为m时，使用标准支持向量机（Support Vector Machine，SVM）进行样本训练需要O（m3）的时间复杂度和O（m2）的空间复杂度。因此数据挖掘应用中，如何快速解决大样本问题是亟待解决的问题。

为了降低时间和空间复杂度，Tsang等人2005年提出大样本数据快速分类算法——核向量机（Core Vector Machine，CVM）［1］。CVM结合计算几何学和SVM训练算法，将QP问题转换成最小包含球（Minimum Enclosing Ball，MEB）问题，然后使用一种有效的（1＋ε）近似算法，从而获得一个近似的SVM最优解。

1 CVM理论

1.1 计算几何意义下的最小包含球

考虑m个D维样本，记作S＝｛x1，x2，…，xm｝，计算几何意义下的最小包含球是指包含S中所有样本的最小球。下面就讨论基于核心集的近似最小包含球。定义B（c，R）表示圆心为c，半径为R的球。设ε＞0，若R≤rMEB（S）且SB（c，（1＋ε）R），则球B（c，（1＋ε）R）是MEB（S）的（1＋ε）逼近，如图1所示，内圆是包含方块点的最小包含球，外圆是内圆的（1＋ε）扩展，且包含所有点，方块点为核心集.从许多拟合问题中发现，如果把整个数据集S的求解转化成对S的一个子集Q的求解，会得到一个精确有效的近似解，其中Q被称为核心集。更精确的定义：若B（c，R）＝MEB（X），且SB（c，（1＋ε）R），则子集XS是S的一个核心集。

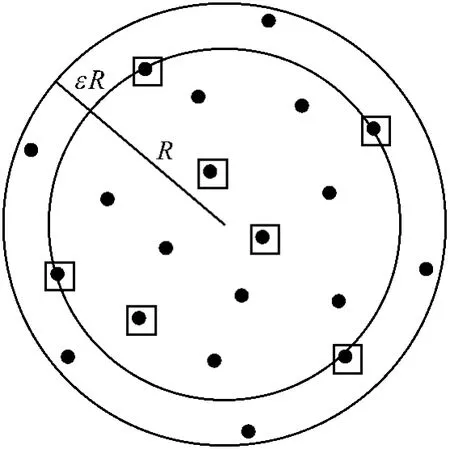
图1 几何意义下最小包含球示例Fig.1 The geometric meaning of the smallest enclosing ball

为获得核心集，Badoiu和Clarkson2002年提出一个简单的计算近似最小包含球的迭代算法［2］，具体步骤如下：在第t次迭代中，得到最小包含球B（ct，rt），之后每次迭代都是把在近似球B（ct，（1＋ε）rt）之外最远点包含进来，直到所有点都包含在B（ct，（1＋ε）rt）中，迭代结束。尽管这个算法简单，但迭代次数和核心集的大小依赖与ε，而不是维数d或者样本规模m。维数d的不相关性，对于运用核方法是非常重要的。样本数m的不相关性，使得算法的时间和空间复杂性增长缓慢。

1.2 最小包含球理论及其核化方法

在上述特征空间中寻求最小包含球MEB（S）等价为如下优化问题：

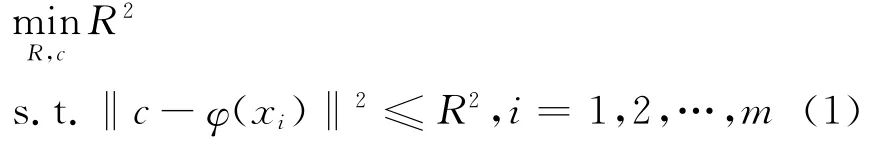
转换为对偶形式：

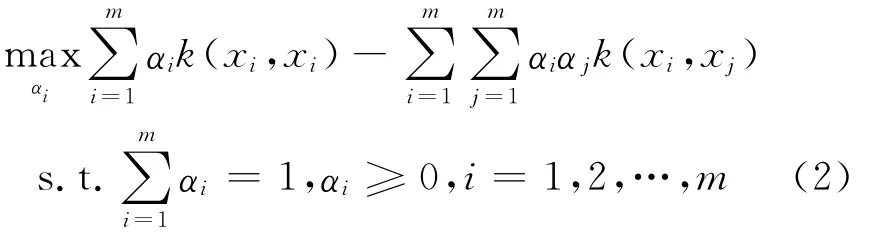
或转换成矩阵形式：

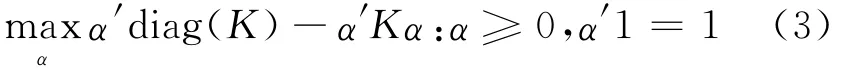
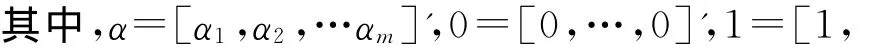
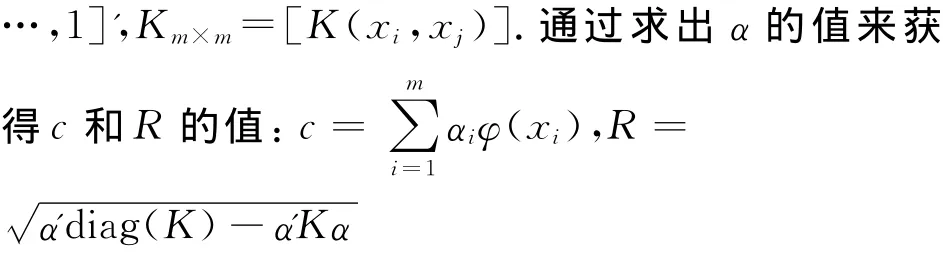
若取高斯核k（x，y）＝exp（－‖x－y‖2／2σ2），则

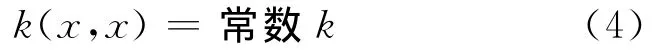
在式（3）中有α＇1＝1的条件，故α＇diag（K）＝k，则式（3）可简化成如下形式：

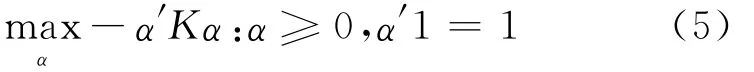
只要满足式（4）和式（5）的QP问题都可看做最小包含球问题，可使用计算近似最小包含球的迭代算法求解。

1.3 SVM简介及其与MEB之间的关系

给定训练集｛Zi＝（xi，yi）｝mi＝1，其中，yi∈｛－1，1｝，SVM优化问题如下：

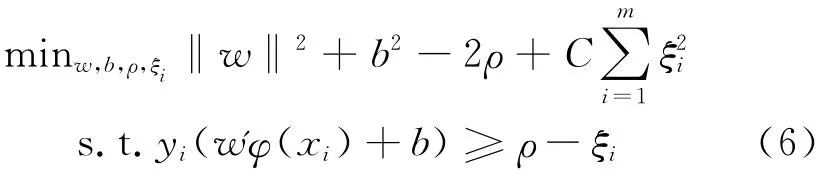
其对应的对偶形式为：

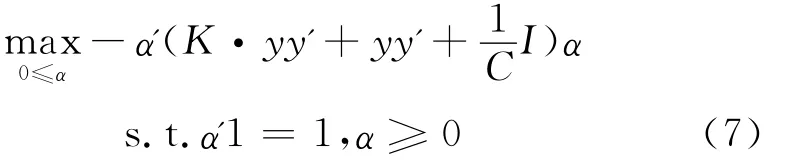
其中，﹒为Hadamard乘积，y＝［y1，y2，…，ym］＇，K＝［k（xi，xj）］。

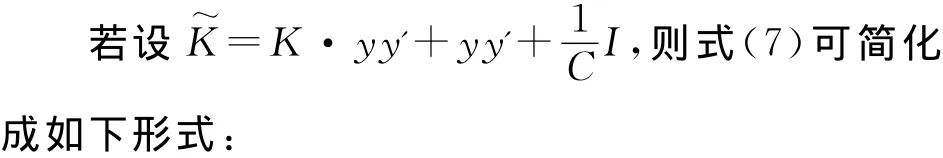
1.4 核心向量机CVM算法

1.4.1 核算法步骤

将核方法转换成相应的MEB问题后，就可使用核向量机快速求解近似最优解。给定训练集｛Zi＝，其中，yi∈｛－1，1｝，因文中采用的是转换后的核，所以下文中的核映射函数用表示，核向量机算法如下：

1.初始化S0、c0和R0。

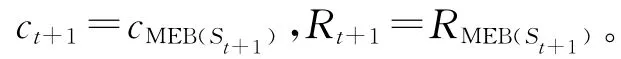
5.迭代次数t加1，返回步骤2。

1.4.2 具体过程

（1）初始化

（2）距离计算

步骤2和3都要进行距离计算，求点zl到中心点ct的距离公式为‖ct－φ（zl）‖2，将c＝（zi）带入上式，得到：

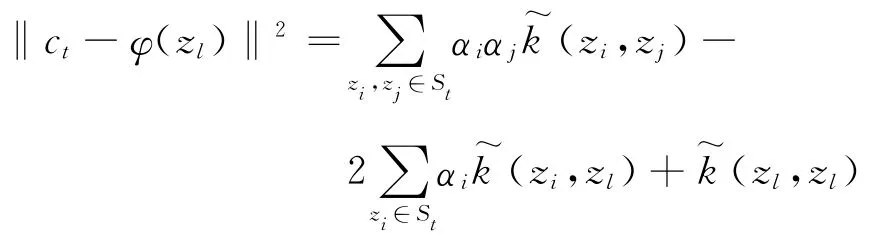
显然，计算距离不需要显式计算φ～（zi），而使用核函数进行计算。然而计算离中心点最远的点需要把所有点到中心的距离都计算一遍，当样本很大时时间花费很高。本文CVM采用由Smola与Scholkopf 2000年提出的一种加速方法［3］。该方法指出，在样本S中随机的找一个样本子集S’，在子集S’中找一个离中心点ct最远点来近似代替S中的最远点。在Smola与Scholkopf的文中指出，当子集大小为59时，最远点包含在S’中的可能性为95%，通过这种方法可大大降低时间复杂度，此方法也可用于初始化步骤。

2 实验与分析

本节实验采用人造香蕉型数据集，如图2所示。CVM需设置的参数有三个，分别是逼近参数ε、核参数σ和C参数。设置方法如下：核参数在网格｛0.5，1，2，4｝，C参数在网格｛0.1，0.5，1，10，100，1 000｝中搜索至最优。

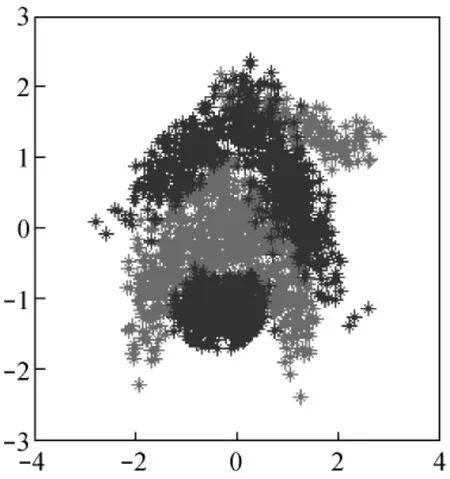
图2 人造香蕉数据集Fig.2 Artificial Banana data set

实验1 逼近参数对CVM的影响验证

取banana样本1 000个进行CVM实验，表1显示了不同逼近参数ε对实验结果的影响。

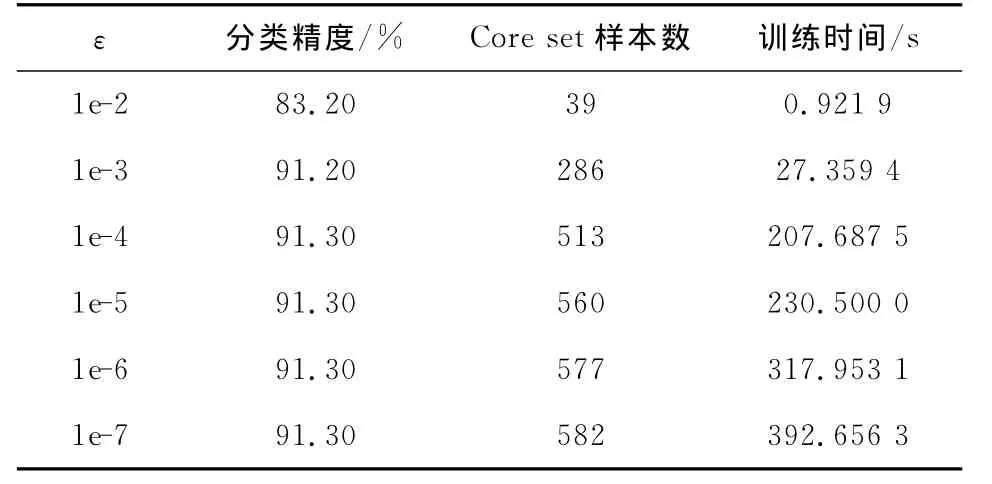
表1 逼近参数ε对CVM的影响（C＝1，σ＝1）Tab.1 Approximation parameters for CVM（C＝1，σ＝1）

文献［1］中指出，ε越小，分类误差越大，随着ε的增大，精度提高的同时训练时间也增加，一般ε取1e－6即可获得较好的分类精度。从表1可以看出，本例的banana数据集，ε取0.5e－3可获得分类精度与训练时间的最佳协调。图3显示了ε取0.5e－3时的分类效果图。

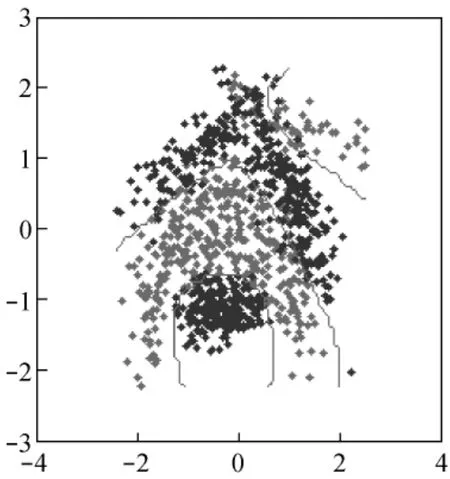
图3 样本规模为1 000时的分类图Fig.3 Classification map（sample size：1 000）

实验2 CVM与SVM的比较实验

下面实验记录了不同训练集规模下，经典SVC与CVM算法的训练时间、测试时间及分类精度。每组实验重复10次，此外还记录了CVM算法的核心集规模。

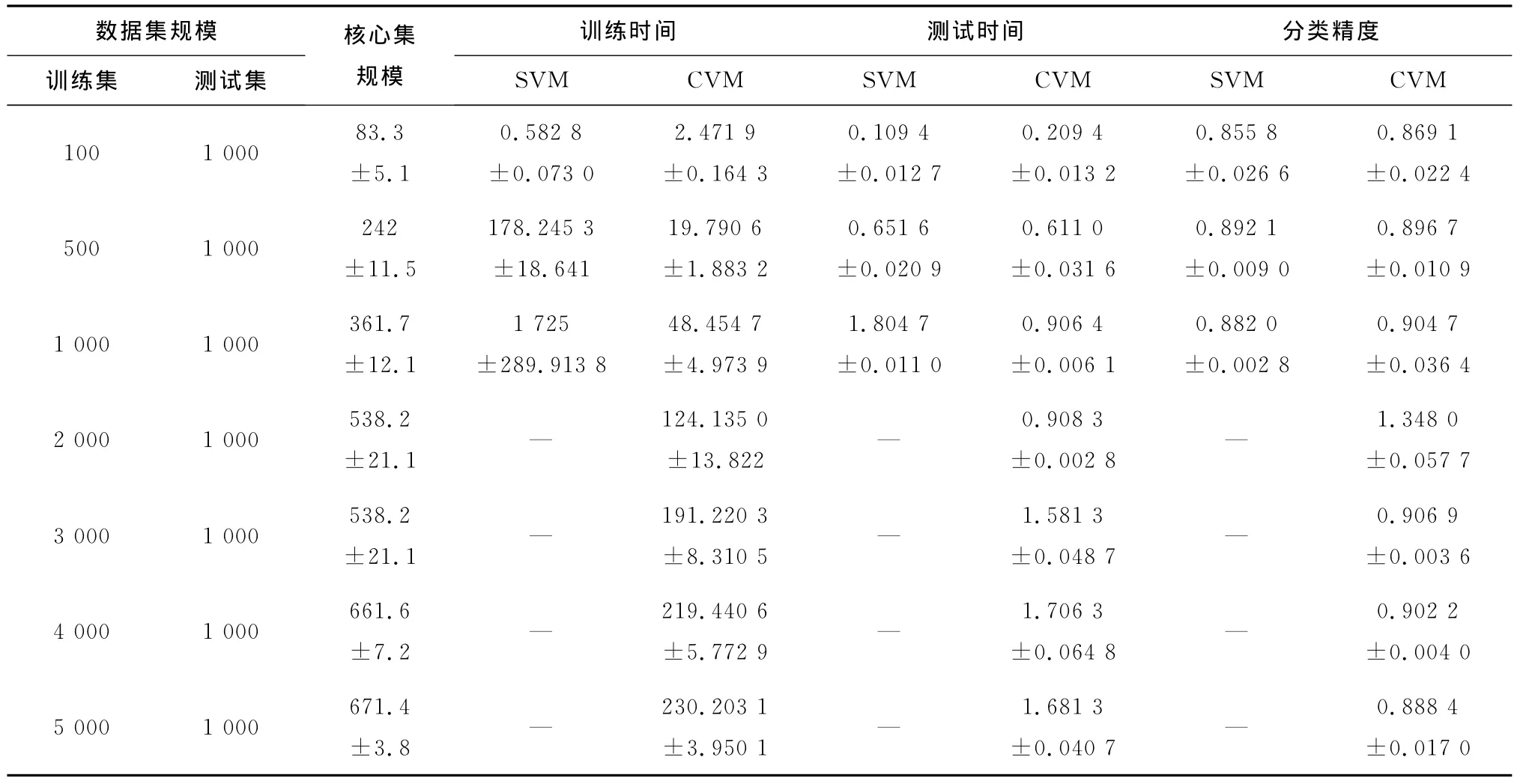
表2 CVM与SVM比较Tab.2 The Comparison of CVM and SVM

从表2可以看出，对于小样本数据集，SVM算法和CVM算法的分类精确度大致相同，且SVM训练时间与测试时间均少于CVM；而对于大样本数据集合，CVM训练及测试时间短，而分类精度还是与SVM相当。使用核心集代替所有样本，存储空间也大规模减小。

3 结束语

核向量机是一种新的模式识别方法，它将核方法转换成等价的MEB问题，并与计算几何学相结合，从而解决了处理大样本所需大量时间和空间的问题。实验表明，与SVM相比，CVM在有效节约运行时间和空间的同时，保证了分类精度。

［1］ Tsang I，Kwok J，Cheung P.Core vector machines：Fast SVM training on very large data sets［J］.J of Machine Learning Research，2005，6（4）：363－392.

［2］ Badoiu M，Clarkson K L.Optimal core sets for balls［J］.Computational Geometry：Theory and Applications，2008，40（1）：14－22.

［3］ Smola A，Schlkopf B.Sparse greedy matrix approximation for machine learning［C］.Stanford，CA：Proc.7th Int.Conf.Mach.Learn.，2000：911－918.

Core Vector Machine Algorithm and its Application

XU Min
（School of Electronic and Information Technology，Wuxi Institute of Technology，Wuxi 214121，China）

According to the training set size m，standard SVM training hasO（m3）time andO（m2）space complexities.In this paper，CVM algorithm is discussed.It transforms the kernel method into equivalent MEB problems，and gets the approximately optimal solutions efficiently by core set.CVM has a time complexity that is liner in m and a space complexity that is independent of m.The result shows that CVM algorithm can handle much larger data sets than existing scale up methods.

Core Vector Machine（CVM）；Support Vector Machine（SVM）；Minimum Enclosing Ball（MEB）；kernel function

TP 18

A

1671－7880（2012）04－0073－04

2012－03－06

许敏（1980— ），女，讲师，博士研究生，研究方向：人工智能与模式识别。