基于EMD与GA-PLS的特征选择算法及应用

李 胜，张培林

(军械工程学院 一系，石家庄 050003)

在对振动信号进行特征选择时，由于其非平稳的特性，导致大量的故障信息淹没在背景中，利用传统的时域或频域方法很难从中提取出有效地故障特征［1－2］。Huang［3－4］提出的一种适用于分析非平稳信号的新方法EMD法，该方法基于信号的局部特征时间尺度，可以把信号分解成若干个固有模态函数(Intrinsic mode function，IMF)之和，分解出的各个IMF分量突出了数据的局部特征，对其分析可以更准确有效地把握原始数据的特征信息。最重要的是分解后的各个IMF分量是经过平稳化处理的。

AR(Auto-regressive)模型是一种时间序列分析方法，该模型参数凝聚了系统状态的重要信息，准确的AR模型能够深刻地、集中地表达动态系统的客观规律。研究表明，AR模型的自回归参数对状态变化规律反映最敏感［5－6］。因此采用AR模型的自回归系数作为特征向量对手动换向阀的工作状态进行分析是非常有效的。由于AR模型适用于平稳信号，并且各个IMF分量是平稳的，所以就可以对各个IMF分量建立AR模型，提取AR模型的自回归系数和残差作为故障特征向量。基于EMD的AR模型已经成功地应用于高压齿轮泵、往复泵等部件的故障特征提取［7－8］。

Leardi等［9－10］提出了把遗传算法(GA)与偏最小二乘法(PLS)结合起来发展的一个变量选择方法(GA－PLS)并将其用于波谱数据中波长的特征选择，获得了令人满意的结果。GA－PLS方法由于结合了GA的全局优化搜索能力和PLS有效地解决变量间多重共线性问题的能力，具有较好的变量选择及模型优化效果，能筛选出与故障信息更相关的特征向量，并且剔除数据中大量冗余和无关的变量。

本文提出了基于EMD和GA-PLS的特征选择算法。该算法首先对振动信号进行EMD分解，得到多个IMF分量，然后对各个IMF分量利用AR模型进行建模，用AR模型的自回归系数和残差作为初始特征向量，然后，利用GA-PLS对初始特征向量进行进一步的特征筛选，最后，以该特征向量为输入，采用三种典型的分类器，建立故障分类器，识别手动换向阀的工作状态和判断故障类型。通过对实验信号的分析，验证了将EMD方法和GA-PLS算法相结合能有效地应用于手动换向阀的故障特征选择，从而为手动换向阀的故障诊断提供了一种新的特征选择方法。

1 EMD方法

EMD方法的目的是通过对非线性、非平稳信号的分解获得一系列表征信号特征时间尺度的固有模态函数，使得各个 IMF是单分量的幅值或频率调制信号［6－7］。每个 IMF满足以下2个条件:

(1)在整个数据段内，极值点的个数和过零点的个数必须相等或最多相差一个;

(2)信号上任意一点，由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值均为零，即信号关于时间轴局部对称。

对任一实信号x(t)进行EMD的具体步骤是:

(1)确定信号x(t)的所有局部极值点，然后用三次样条插值分别将所有的局部极大值点和局部极小值点连接起来，形成上包络线和下包络线，这两条包络线包络了所有的信号数据。m1(t)，用x(t)减去m1(t)得:

(2)计算上、下包络线的平均值，记为 m1(t)，求出:

如果h1(t)是一个IMF，那么它就是信号x(t)的第一个IMF。

(3)如果h1(t)不是一个IMF，则将h1(t)作为原始数据，重复步骤(1)、(2)得到上、下包络线的平均值，记为m11(t)，计算h11(t)=h1(t)－m11(t)，并判断是否满足IMF的条件，如不满足，则重复循环，计算h1k(t)=h1(k－1)(t)－ m1k(t)，直到 h1k(t)是一个 IMF。记c1(t)=h1k(t)，则c1(t)为信号x(t)的第一个IMF。

(4)将c1(t)从x(t)中分离出来，得到:

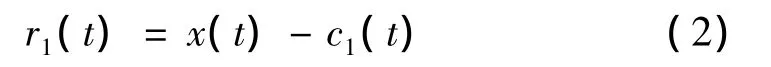
将r1(t)作为原始数据，重复步骤(1)－(3)，得到第二个IMF c2(t)。重复循环n次，到信号x(t)的n个IMF，于是有:

当rn成为一个单调函数不能再从中提取满足IMF条件的分量时，循环结束。这样信号可表示:

其中，rn称为残余函数，代表信号的平均趋势。

2 GA-PLS算法

GA-PLS算法对变量的选择过程由以下五个基本步骤组成。

(1)随机地给每个染色体赋值，确定染色体初始长度，1代表选中相应的变量，0代表变量未被选中。染色体长度的具体数目由需要解决问题的维数决定;

(2)确定每个染色体的个体适应度，由以下的内部预测模型给出评估:

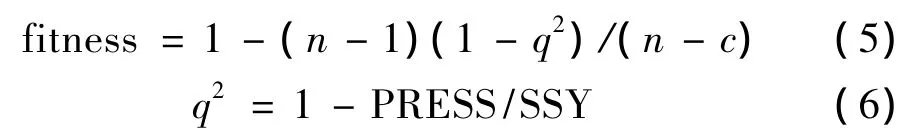
q2是通过留一法得到的交叉验证值，SSY是变量的平方和，PRESS是留一法交叉验证后的预测平方和，n是样本个数，c是被选择出的变量个数。不但模型的可靠性由q2决定，而且被选择的变量个数也由适应度函数决定。

(3)具有较高适应度的染色体均选自以任意比例的长度。其他必要的染色体，通过交叉和变异得到，从而弥补下一代的数量，以确保种群的多样性。

(4)在一个交叉过程中，随机挑选一对染色体，对其单独分割，互相交换，并以预先确定的交叉频率合并。在一个突变过程中，对每一个染色体的二进制模式改变一个小概率。

(5)根据个体适应度，对后代重新进行安置并取代上一代的位置。重复运行以上的四个步骤(步骤2到步骤(5)直到世代的数目达到给定的最大数目的世代［9－10］。图 1 描述了GA-PLS进行特征选择的过程。

GA-PLS算法有以下的优点［11－12］。与其他方法相比，在全局搜索能力方面，GA-PLS方法能更精确地找到优化的解决方法。偏最小二乘法能解决多元回归多重共线性问题。当样本点个数比变量少时，也对回归模型进行了分析。因此，GA-PLS算法结合了两种算法的优点，并大量地成功地应用在不同的数据类型的特征选择。

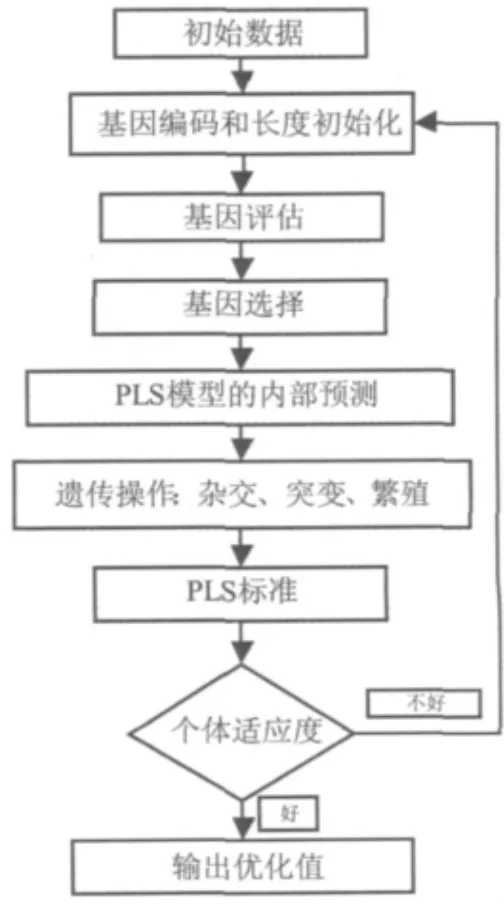
图1 GA-PLS的特征选择过程Fig.1 Feature selection process by GA-PLS

采用根均方误差(root-mean-square error，RMSE)作为误差函数，根据以下的公式计算:

其中，yi是训练集中的理想输出，f(xi)是通过留一法交叉验证得到的实际输出，N是训练集中的样本数目。

在GA-PLS算法中，根据经验值，影响其性能的参数的设置如下［9－10］:在初始群中每条染色体平均由5个变量组成，种群大小30，迭代次数100，突变概率0.01，交叉概率 0.5，遗传迭代次数 100。

3 基于EMD和GA-PLS的特征选择算法

基于EMD和GA-PLS的特征选择算法过程如下。

(1)分别在各个工作状态下，按一定的采样频率fs进行N次采样，得到振动信号。

(2)对每一种状态下的每一个训练样本进行i层EMD 分解，得到 i个 IMF 分量 c1，c2，…，ci。

(3)对每一个IMF分量ci建立AR模型，采用FPE准则确定模型的阶数m，由最小二乘法估计自回归参数 φik，k=1，2，…，m 和模型的残差 ei，提取 φik和 ei形成初始故障特征向量，因此，得到一个 l×(m+1)的矩阵:Ai={φi1，…，φim，ei}。

(4)GA-PLS算法对 l×(m+1)的矩阵进行特征选择以减少维数，并得到更有效的特征向量，得到的新的特征向量Bi作为输入量。

(5)采用分类器对由故障特征向量Bi组成的训练样本进行训练，得到对应的分类器，用测试样本进行测试，得到输出结果。基于EMD和GA-PLS的特征选择算法流程如图2所示。

图2 基于EMD和GA-PLS的特征选择算法流程Fig.2 The flow chart of feature selection

4 实验验证

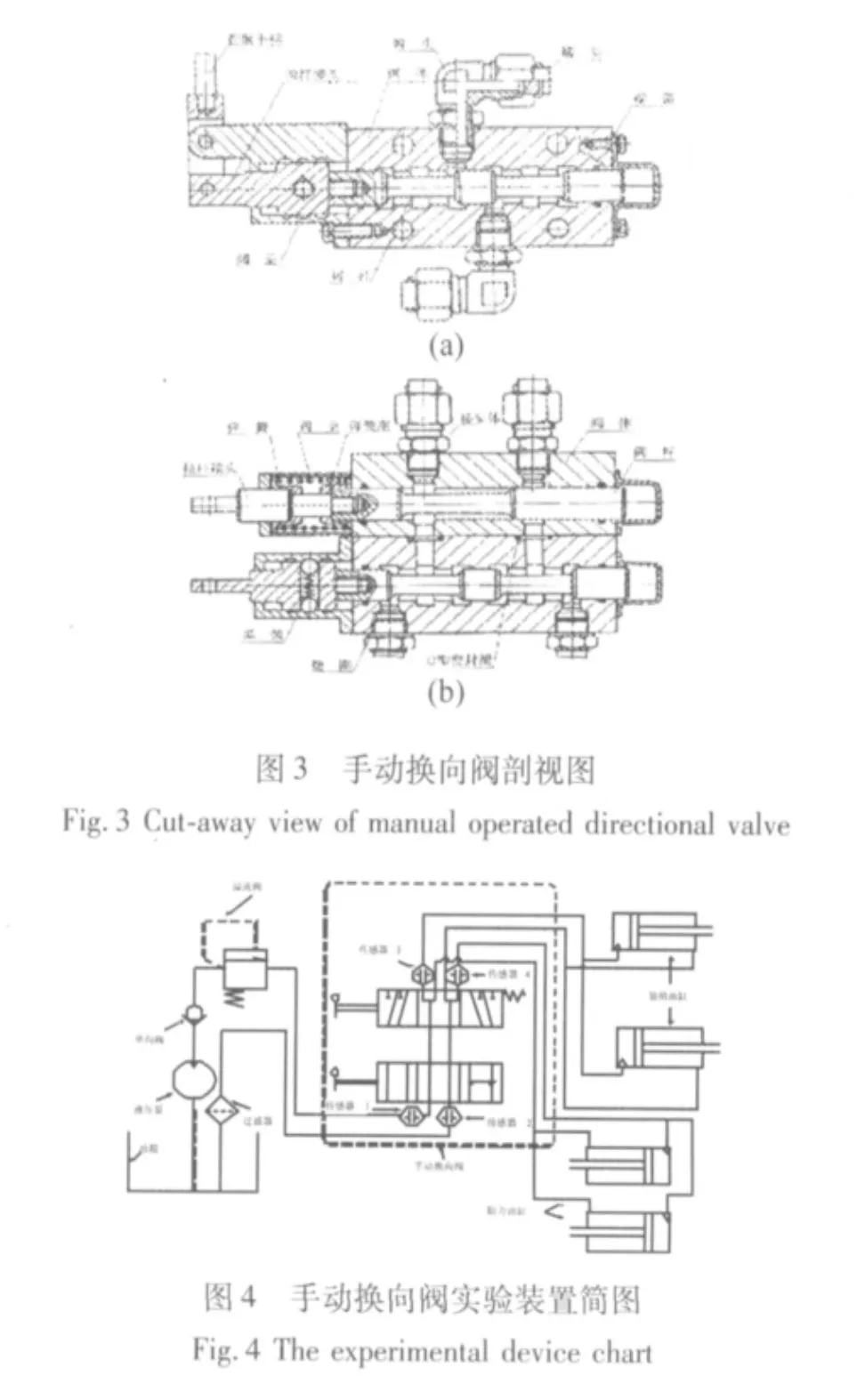
对上述理论分析进行实验验证。实验装置为液压系统综合检测与试验设备。采用某型工程车辆的手动换向阀作为实验器件，图3为该手动换向阀的结构图。在手动换向阀进油口、出油口、装填回路管路和助力回路管路上，安装压电加速度传感器，传感器型号为CAYD－185。手动换向阀实验装置、传感器测点布置与信号采集装置如图4所示。该装置能模拟正常状态、装填故障、助力故障等多种故障状态，压电加速度传感器测量手动换向阀油管管口的振动信号。

在液压系统综合检测与试验设备上，对手动换向阀三种工作状态分别采样。实验中，电动机转速为1 000 r/min，采样频率为 10 kHz，采样时间为 0.41 s，分别采集正常状态、装填故障和助力故障三种工作状态下的振动信号各50组数据，其中，20组数据作为训练样本，30组数据作为测试样本。

对振动信号进行EMD分解。由于EMD方法是一种主成分分析方法，其主要的故障信息集中在前几个IMF分量。因此，本文进行11层EMD分解，并选用了前6个IMF分量。对3种工作状态信号的前6个IMF分量分别建立AR模型，采用FPE准则确定模型阶数m。在本文的实验中，AR模型的阶数设定为8阶。因此，手动换向阀的故障信息主要包含8个AR模型系数和残差作为特征参数。图5为三种工作状态的振动信号对比。以装填故障的振动信号为例，图6表示了该信号的11个IMF分量。

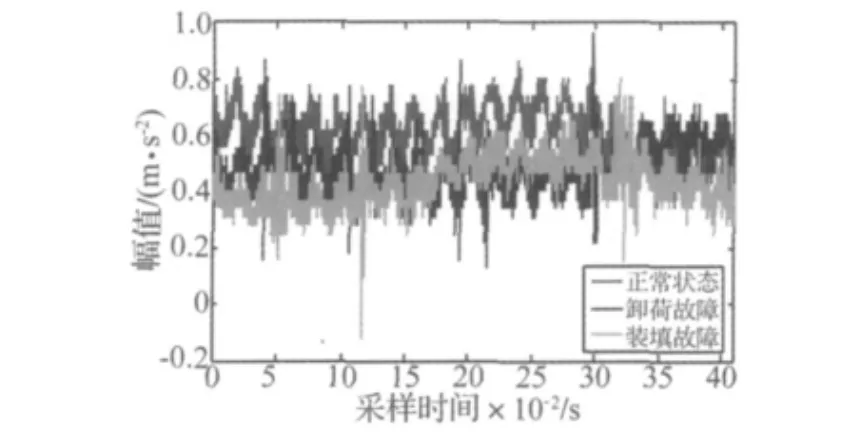
图5 三种工作状态的振动信号Fig.5 The vibration signals of three states

表1给出的是三种状态下各一个手动换向阀振动信号的初始特征向量(由于篇幅关系，其它特征向量未列出)，然后将初始特征向量作为输入，利用GA-PLS特征选择方法进行进一步的筛选。

表2给出每个特征向量对应的个体适应度值。从表中可以得出不同故障状态的特征向量。表3为经GA-PLS方法筛选后的特征向量Bi。将表1和表3进行对比后发现，经过GA-PLS方法筛选后，特征向量数量大大减少，维数大大降低，有利于分类。

图6 装填故障的IMF分量Fig.6 The IMFs ofloading fault states

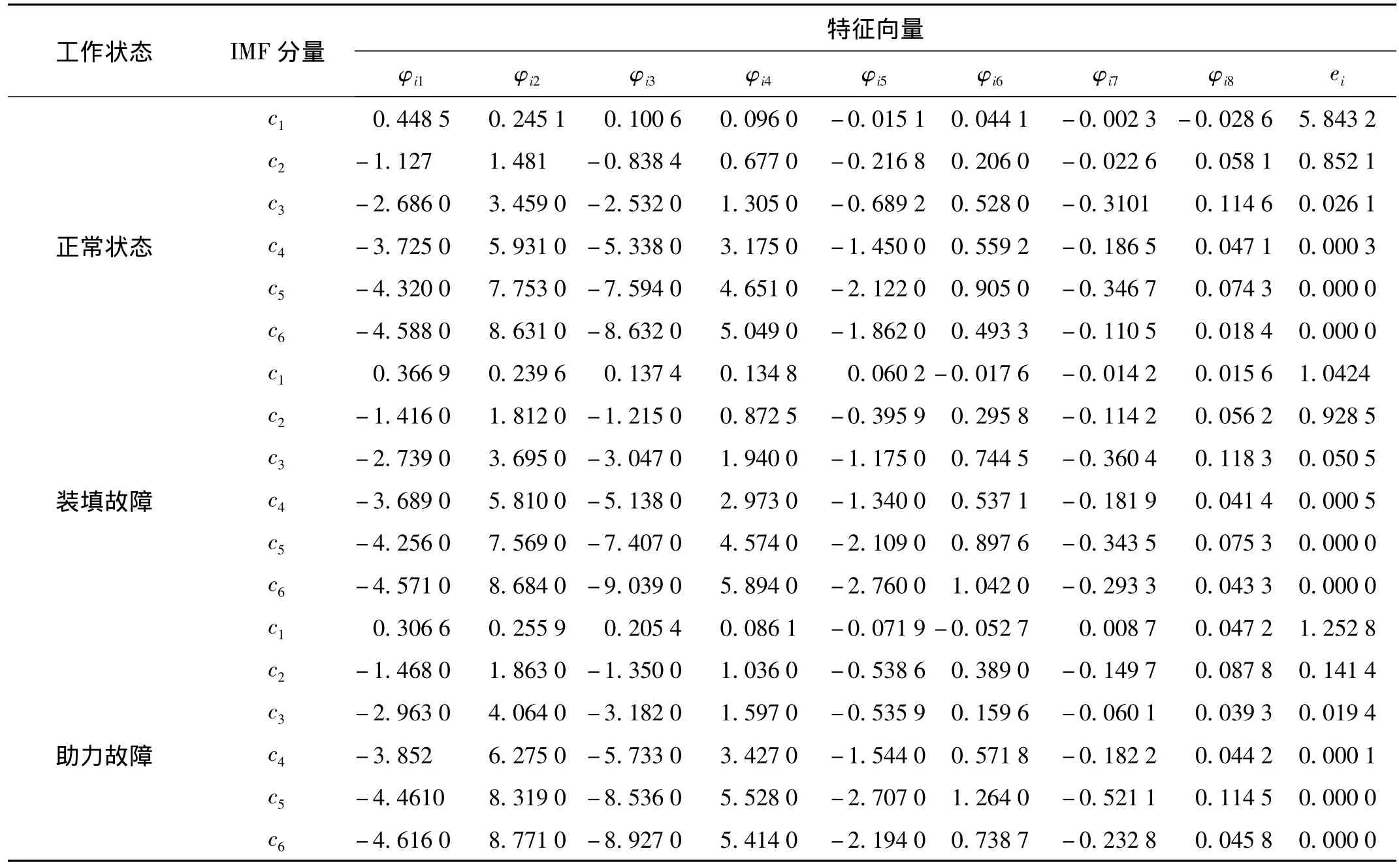
表1 手动换向阀各种状态下的特征向量Tab.1 The parameters of AR model for IMFs of each fault state

表2 被选择特征向量对应的个体适应度值Tab.2 Selected features and corresponding fitness values by GA-PLS

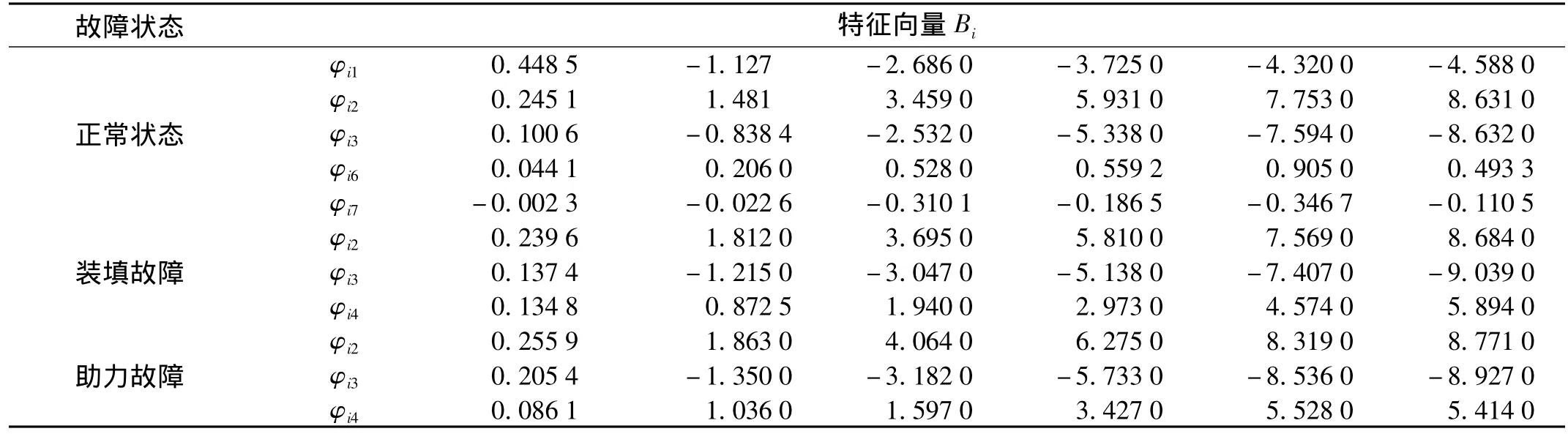
表3 经GA-PLS选择后的特征向量Tab.3 The new parameters selected by GA-PLS

表4 三种分类器对特征向量的分类结果Tab.4 The results by using three classifiers with two methods

为了说明GA-PLS方法的有效性，采用三种典型分类器对未经GA-PLS选择的特征向量和经GA-PLS选择的特征向量进行分类，结果如表4所示。从表4可以看出，用经GA-PLS选择的特征向量能够对样本进行正确率为99%的故障分类，分类效果比用未经GA-PLS选择的特征向量要好很多，而且在分类时间方面，GAPLS方法节省了大量的时间，可对故障进行在线分类。因此，基于EMD和GA-PLS的特征选择算法对手动换向阀故障诊断是有效的。

5 结论

EMD方法是一种能把非平稳信号转变成平稳信号的信号处理方法。AR模型是一个信息的凝聚器，可将手动换向阀振动信号的特性及工作状态都凝聚其中，因而可依据它对手动换向阀的工作状态进行识别。EMD方法和AR模型相结合能解决振动信号的非平稳特性和特征向量不能反映故障状态的问题。同时，GAPLS方法能很好的地克服特征间相关的影响。该方法能得到较好RMSE值，较短的分类时间和较高的分类准确率。与其他特征选择方法相比，实验结果清楚地显示了基于EMD和GA-PLS特征选择方法能有效地应用于手动换向阀的故障诊断，为手动换向阀的故障诊断提供了一种新的方法。

［1］ Mcfadden P D.Window function for the calculation of the time domain averages of the vibration of the individual planet gears and sun gear in an epicyclic gearbox［J］.ASME Journal of Vibration and Acoustics.1994，116 179－187.

［2］ 林 京，刘红星，屈梁生，等.信号时域平均处理中的若干问题探讨［J］.振动工程学报，1997，10(4):446－450.

［3］ Huang N E，Shen Z.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc.R.Soc.Lond.A，1998，454:903－905.

［4］ Huang N E，Shen Z，Long S R.A new view of non-linear water waves:the Hilbert spectrum［J］.Annu Rev Fluid Mech，1999(31):417－457.

［5］ Ljung L.System Identification:Theory for the User(2nd Edition)［M］. Beijing， China:Tsinghua University Press，2002.

［6］ 贺湘宇，何清华，邹湘伏，等.基于RBF网络和ARX模型的液压系统故障诊断方法［J］.系统仿真学报，2009，21(1):282－285.

［7］ 江四厚，陈小虎，王汉功，等.基于Hilbert-Huang变换的振动信号特征提取［J］.机床与液压，2008，36(11):199－201.

［8］ 徐长航，刘吉飞，陈国明，等.经验模态分解和魏格纳－维利分布在往复泵泵阀振动信号特征提取中的应用［J］.中国石油大学学报(自然科学版)，2010，34(3):99－103.

［9］ Gonzalez A L.Leardi R.Genetic algorithms applied to feature selection in PLS regression:how and when to use them［J］.Chemometr Intell Lab，1998，41(2):195－208.

［10］ Leardi R.Application of genetic algorithm-PLS for feature selection in spectral data sets［J］.J Chemometr，2000，14(5/6):643.

［11］ Azizi A，Niazi A，Leardi R.A comparative study between PLS and OSC-PLS in the simultaneous determination of lead and mercury in water samples:effect of wavelength selection.Canadian Journal of Analytical Sciences and Spectroscopy，2007，52(6):365－374.

［12］ Khajehsharifi H，Pourbasheer E.Genetic-algorithm-based Wavelength Selection in Multi-component Spectrophotometric Determination by PLS:Application on Ascorbic Acid and Uric Acid Mixture［J］.Journal of the Chinese Chemical Society，2008，55:163－170.