三维振动里兹法在变幅杆谐振特性分析中的应用研究
2012-09-15秦慧斌王时英李向鹏
秦慧斌,吕 明,王时英,李向鹏
(1.太原理工大学 机械工程学院,太原 030024;2.中北大学 机械工程与自动化学院,太原 030051)
超声加工能降低切削抗力、减少表面硬化,改善工件表面质量,提高刀具寿命和加工效率[1],已广泛应用于脆硬材料如:陶瓷、玻璃、钛合金、淬火钢等的车、铣、磨、珩磨、钻削加工。在超声加工中,超声振动系统一般由超声波发生器、换能器、变幅杆以及加工工具或工件等组成,是超声加工工艺系统的核心部件;振动系统性能直接影响着超声加工质量。超声振动系统中变幅杆的主要作用是把机械振动的质点位移或速度放大,或者将超声能量聚集在较小面积上。变幅杆的设计能否实现超声振动系统的谐振是振动系统设计的关键。目前,超声加工技术中所应用变幅杆的设计是从一维变截面杆的运动方程出发忽略剪切变形和转动惯量对振动的影响[2],其工程应用局限于变幅杆横向尺寸小于1/4纵波长。
中小模数齿轮超声加工中,加工分度圆小于100 mm,厚径比大于0.3的齿轮(齿轮轴)适宜利用纵-纵(扭)振动方式设计振动系统;分度圆直径大于100 mm,且厚径比小于0.2的齿轮,适宜利用纵-弯振动方式设计振动系统进行超声滚齿、剃齿、珩齿加工。由于齿轮加工机床传动链的复杂性和精确性,超声振动大都加在工件齿轮上,变幅杆的另一作用作为齿轮超声加工的夹持芯轴[3-4]。变幅杆的截面寸已超出1/4波长,已不能利用一维振动理论进行设计。
文献[5]基于瑞利近似理论假设,采用能量修正法对大尺寸变幅杆进行了频率修正,此方法适用于变幅杆截面尺寸小于1/2波长,可以满足工程上的精度要求,但只研究了变幅杆的纵向振动,没有涉及变幅杆的弯曲及扭转振动。在铁摩辛柯理论下,等截面梁的弯曲振动解已求出,变截面变幅杆的分析比较复杂,很难得到解析解[6]。
里兹法是一种无网格划分的数值求解方法,它将数理方程求解变成定积分运算和代数方程组求解,具有简易性,适应于编制程序和计算机计算。随着计算机性能和分析程序的高效化,越来越多的学者基于三维弹性振动里兹法对杆、梁、盘或板的振动分析进行了研究。文献[7-8]基于三维弹性振动理论,采用能量变分法研究了线性、二次、三次方程截面形状的梁以及中心带孔的圆锥梁的振动特性,并对多项式函数的收敛性进行了深入计算分析;文献[9]采用三维弹性振动理论和里兹能量变分法研究了均匀截面,不同长径比圆柱的横向振动和板的弯曲振动,并与一维欧拉-伯努利、铁摩辛柯、有限单元法的求解结果进行了对比分析。
本文基于三维弹性振动理论,采用能量变分里兹法统一变幅杆的扭转、纵向、弯曲振动的求解方法,并计算不同长径比、不同面积系数圆截面变幅杆的固有频率。对大、中、小圆截面指数形变幅杆的谐振频率,从一维欧拉-伯努利振动求解理论、三维振动里兹法、有限单元法、模态实验角度进行对比分析,为大功率超声振动加工领域的大截面变幅杆设计提供了一种有效设计方法。
1 变幅杆的三维弹性振动里兹法求解原理
1.1 变幅杆振动分析模型与动力学公式
带有圆形变截面的变幅杆,左端z=0半径为R1,右端z=L处截面半径为R2,L为变幅杆的长度,θ为周向角度,圆柱面坐标系见图1。变幅杆各坐标取值范围如下:
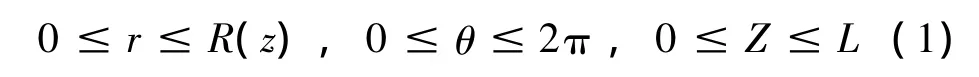
图1柱面坐标系(r,θ,z),变幅杆在振动时,有沿坐标轴的三个位移分量 ur,uθ,uz;六个应变分量 εr,εθ,εz,γrθ,γθz,γzr;六个应力分量 σr,σθ,σz,τrθ,τθz,τrz。这15个未知数将满足由三维动力学运动方程式(2)、物理方程式(3)、几何方程式(5)组成的15个方程[10]。其中三维动力学运动方程为:
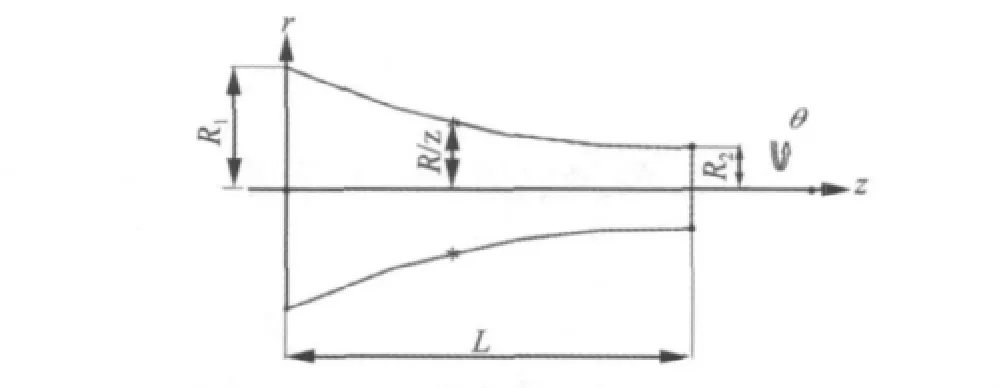
图1 圆截面变幅杆(r,θ,z)柱面坐标系Fig.1 A representative horn having circular cross-section and the cylindrical coordinate system(r,θ,z)
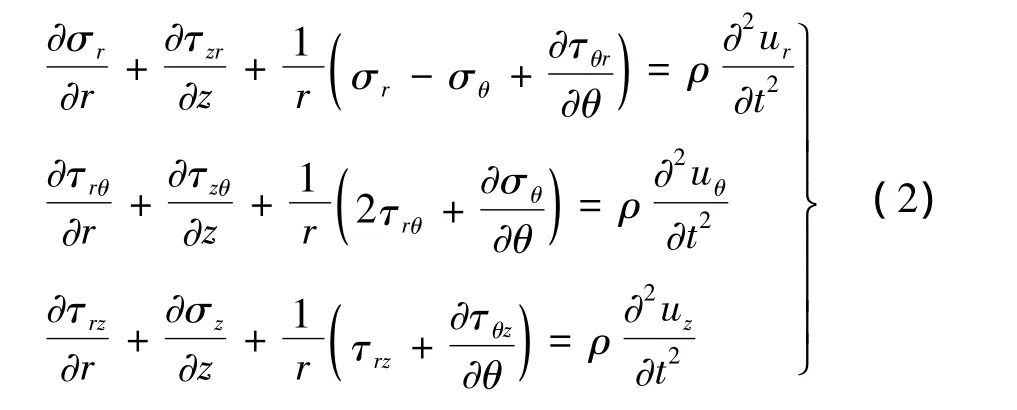
对于各向同性线弹性材料,应力、应变满足物理方程:
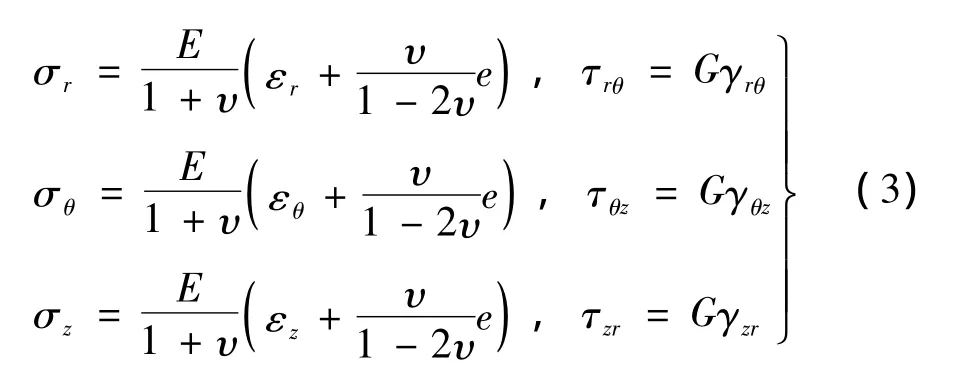
其中:e=εr+εθ+εz为体积应变,ν为泊松比,G 为剪切弹性模量,G与ν二者存在关系:

位移分量和应变分量满足以下几何方程:
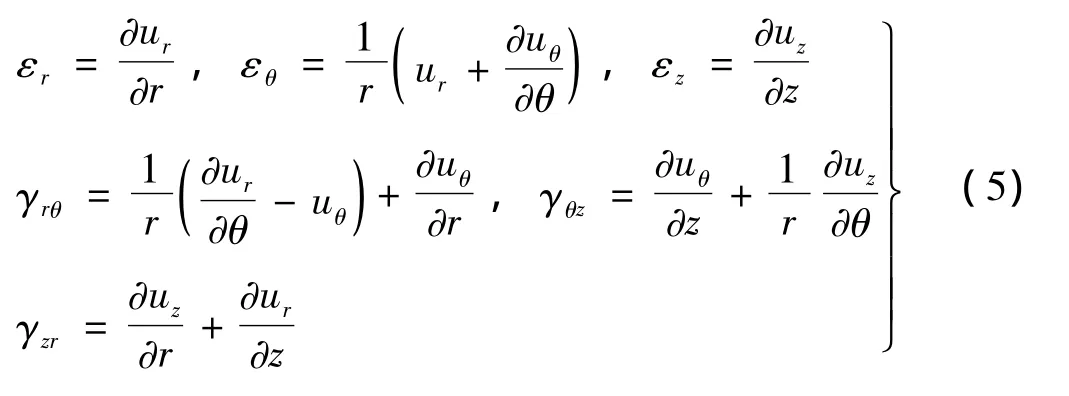
将式(3),式(5)代入式(2),可求得关于未知变量ur,uθ,uz的二阶变系数偏微分方程,一般情况下理论求解十分困难,可以采用能量变分数值法求解[7]。
当r=0时,1/r会出现奇异值,将式中r的取值范围由0≤r≤R(z)调整为0<r≤R(z)。
振动变形体,因受力发生形变,内部产生应变和应力,此时体内具有弹性形变势能。其整个区域内应变势能V如下:

将式(3),式(5)代入式(6)可求得用应变表示的应变能。
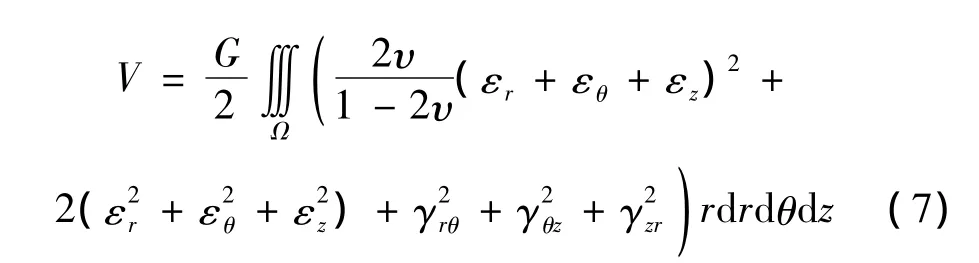
动能表达式如下:
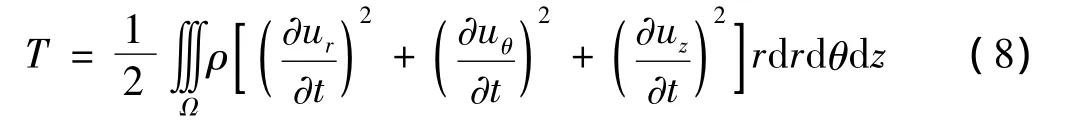
为了简化公式推导与设计计算,将r,z坐标转化为无量纲坐标,令Ψ=r/(R1+R2),ζ=z/L,圆柱柱面坐标值范围如下:
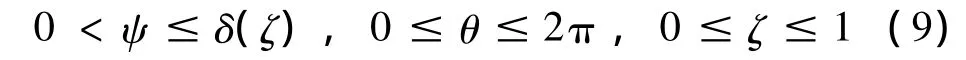
圆锥变幅杆、圆截面指数形、悬链形变幅杆δ(ζ)分别为:
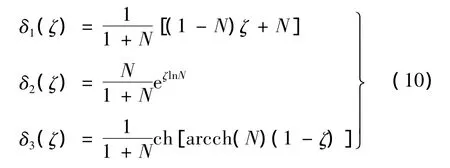
其中:N=R1/R2为面积系数,对应的变幅杆配置模型如图2所示。
1.2 振幅
对于不计阻尼的非均匀圆截面变幅杆自由振动,其弯曲、扭转、纵向振动的振幅分别可由下式表示[7]:
弯曲振动的振幅:
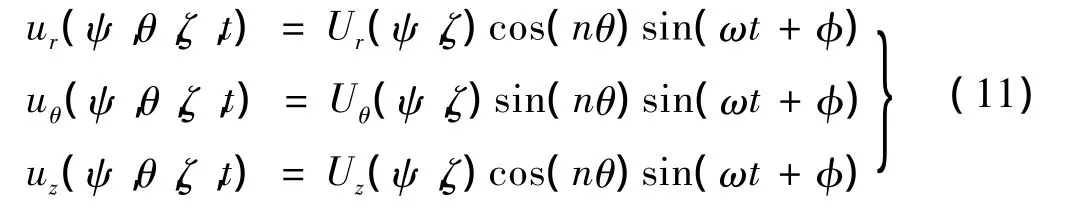
扭转振动的振幅:
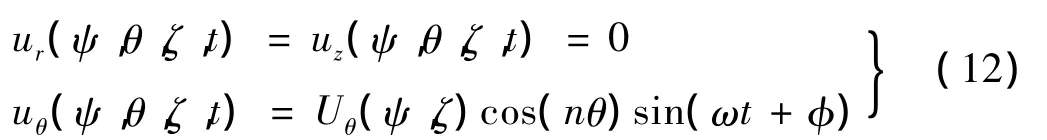
纵向振动的振幅:
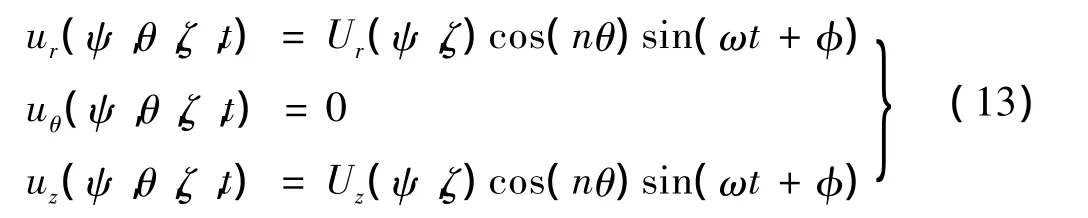
式中:Ur,Uθ和Uz是ψ和ζ的位移函数,ω为圆频率,φ是由初始条件所确定的角位移。n为圆波数,以θ为周期,式(11)中 n=(1,2,3,…,∞),式(12)、(13)中 n=0。
1.3 应变势能
分别将式(11)、(12)、(13)代入式(5)后,再代入式(7),可以得到变幅杆纵向、弯曲振动的一个振动周期内的最大应变势能为:
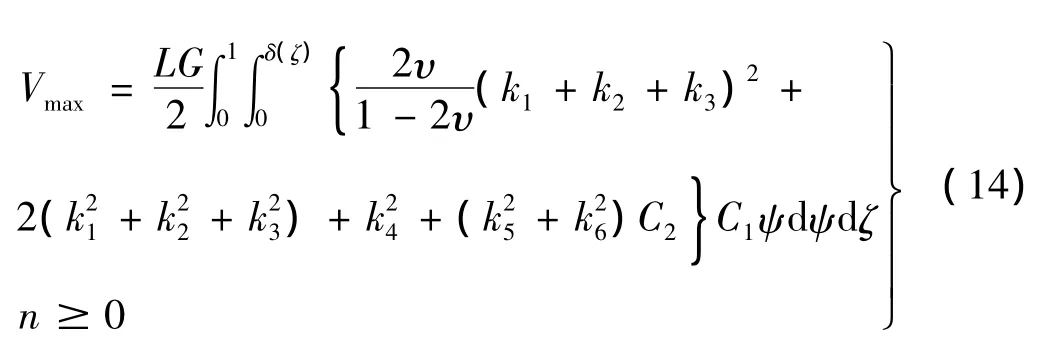
n=0为纵向振动最大应变势能公式,n≥1为弯曲振动最大应变势能公式。
其中:
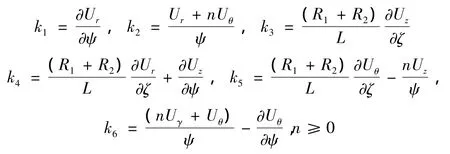
扭转振动的一个振动周期内的最大应变势能为:
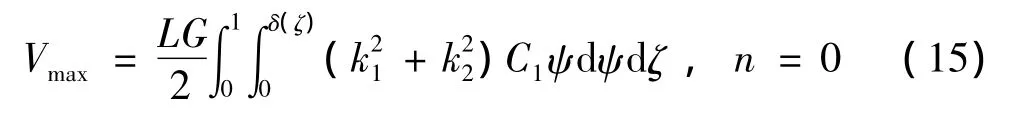
其中:
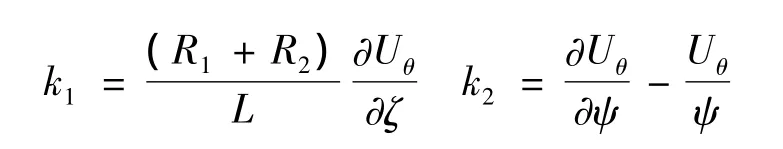
1.4 动能
分别将式(11)、(12)、(13)代入式(5)后,再代入式(8),可以得到变幅杆弯曲、纵向振动的一个振动周期内的最大动能表达式:
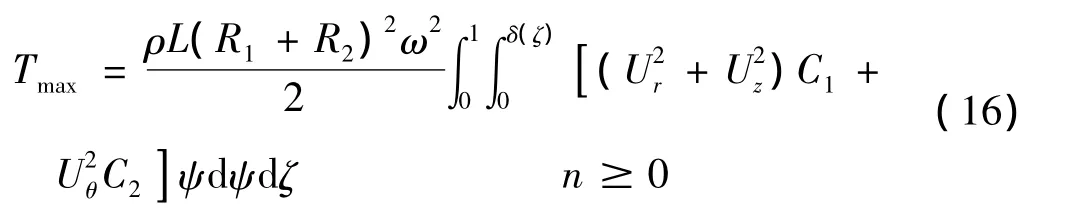
其中:n≥1为弯曲振动最大动能公式,n=0为纵向振动最大动能公式。扭转振动的一个振动周期内的最大动能表达式为:
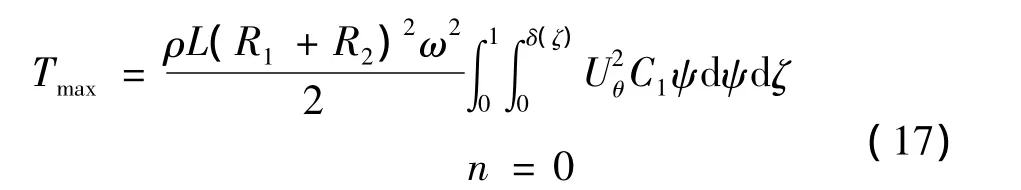
式(14)~式(17)中C1和C2是常数,由下式确定:

1.5 振型函数
设式(11)~ 式(13)中的 Ur,Uθ,Uz的振型函数表达式为:
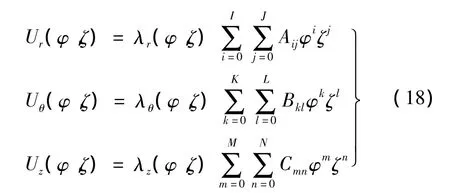
式中:i,j,k,l,m,n 取正整数,I,J,K,L,M,N 为计算所需级数的最大值。Aij,Bkl,Cmn为级数相应系数,λr,λθ,λz为影响因数,其值由变幅杆的边界条件确定:
(1)两端自由振动时λr=λθ=λz=1;
(2)左端固定其余边界自由时λr=λθ=λz=ζ;
(3)右端固定其余边界自由时λr=λθ=λz=ζ-1;
(4)两端都固定时 λr=λθ=λz=ζ(ζ-1)。
随着级数项数的增加,级数函数包含了变幅杆所有的三维振动形态。式(18)将会收敛于理论解。
1.6 特征值方程的求解
应用哈密尔顿原理得:
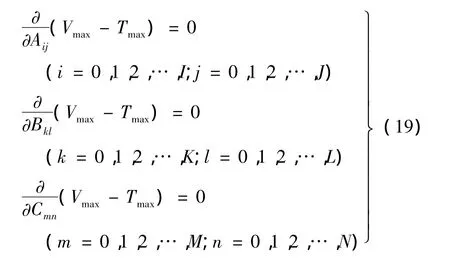
式(19)产生了(I+1)(J+1)+(K+1)(L+1)+(M+1)(N+1)个,以 Aij,Bkl,Cmn为未知系数的频率方程式为:
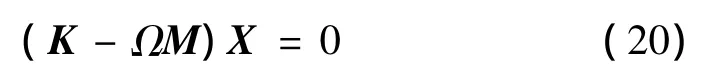
也即变幅杆的频率方程,若确定变幅杆的工作频率可由此方程解得变幅杆的设计参数,若已知变幅杆的尺寸参数则可以解得其谐振频率。K,M分别为弹性刚度矩阵和质量刚度矩阵。Ω为特征值。振型系数向量由式(21)确定。要取得非零解,系数矩阵行列式值应为零,由此可求得变幅杆的固有频率ω。所求得的频率特征值是理论精确值的上限;把ω代入式(20),求出系数Aij和Bkl,Cmn,进而可以求得每一频率对应的振型、变幅杆的位移节点、放大系数、形状因数等性能参数。
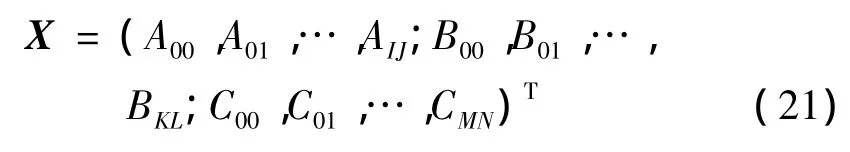
2 变幅杆固有圆频率的计算分析
利用Matlab7.1编程,三维振动里兹法所求得不同长径比、不同面积系数圆锥形、圆截面指数形和悬链形变幅杆的扭转、纵向、弯曲自由振动第一阶非零无量纲固有圆频率(以ωL表示)如表1,2,3 所示。其中泊松比ν=0.3,δ为变幅杆长径比,δ=L/(R1+R2);N为面积系数,N=R1/R2。I=J=K=L=M=N=4,计算机硬件配置内存2X1024M RAM,处理器为Intel(R)Core(TM)i3-2330M CPU。0T表示n=0变幅杆扭转振动,0L表示n=0变幅杆纵向振动,1B表示n=1的变幅杆弯曲振动。
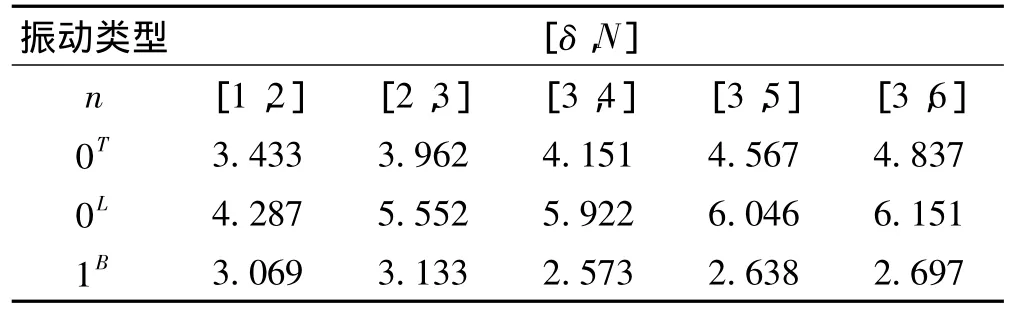
表1 圆锥形变幅杆自由振动第一阶固有频率表Tab.1 The first inherent frequencies of conical horns for free vibration
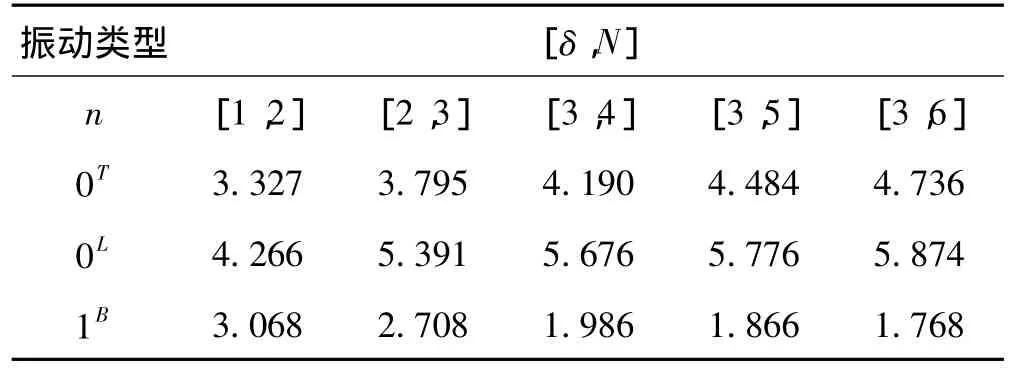
表2 圆截面指数形变幅杆自由振动第一阶固有频率表Tab.2 The first inherent frequencies of exponential horns having circular-section for free vibration
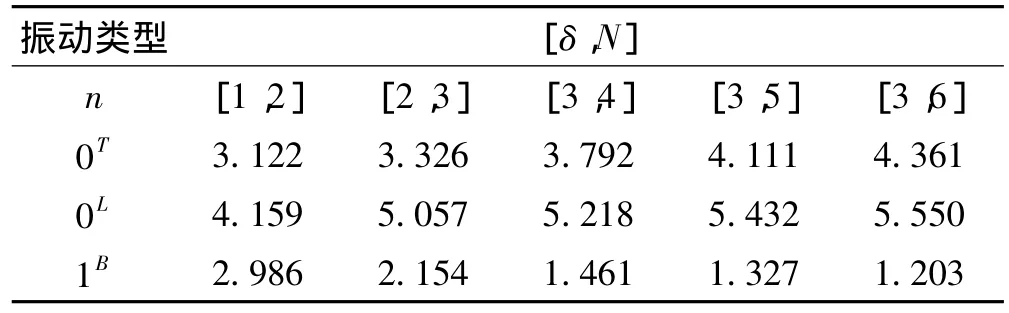
表3 悬链形变幅杆自由振动第一阶固有频率表Tab.3 The first inherent frequencies of catenary horns having circular-section for free vibration
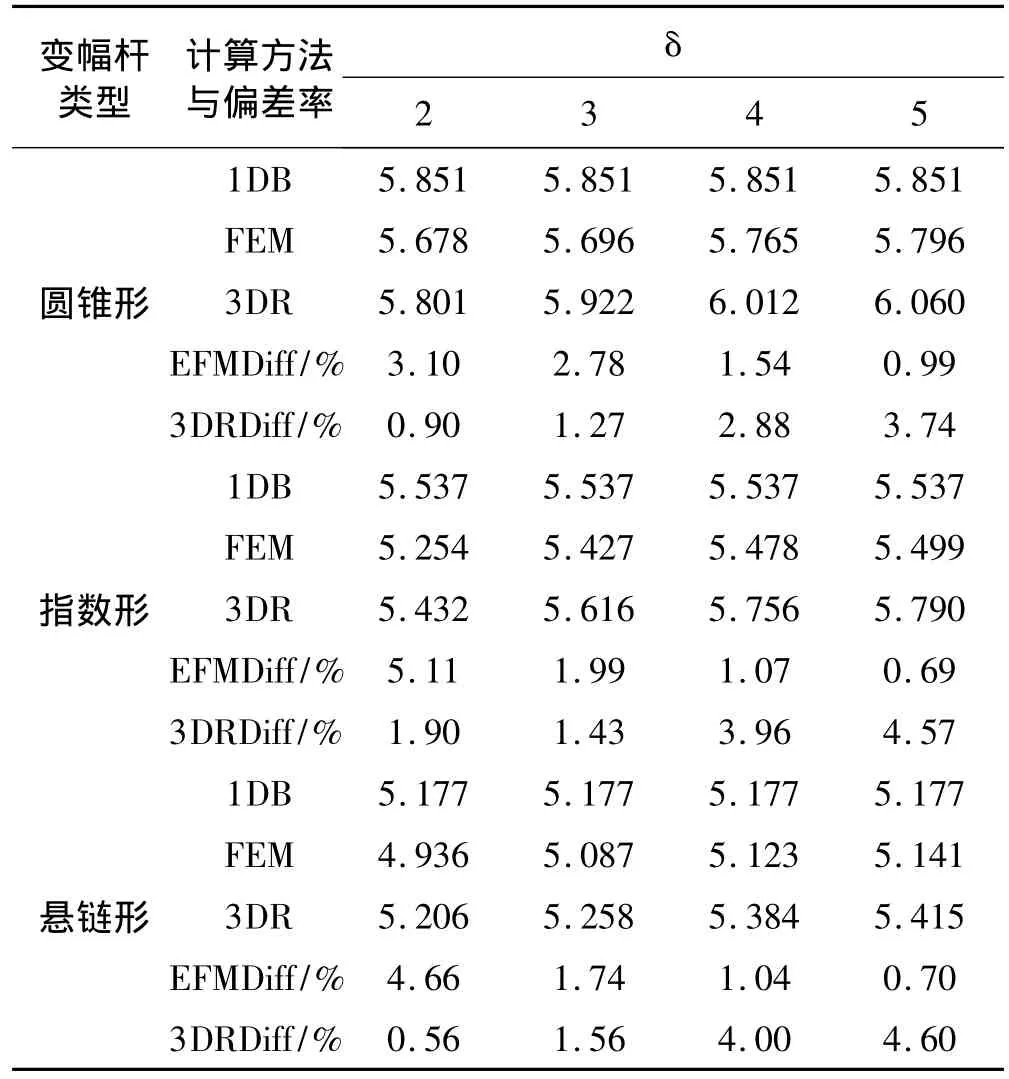
表4 圆截面变幅杆第一阶自由纵向振动求解及偏差对比表Tab.4 Comparison of non-dimensional frequencies of horns with circular cross-section for the first longitudinal vibration
表4为面积系数 N=4,长径比 δ分别取2,3,4,5的圆锥、指数、悬链形变幅杆的纵向振动第一阶非零无量纲固有圆频率(以ωL表示)与偏差对照表。1DB表示一维振动欧拉-伯努利计算方法,3DR表示三维振动里兹法,FEM表示有限单元法。FEM偏差率,3DR偏差率3DRDiff(%)从表4偏差计算结果横向比较表明:随着δ的增大,FEM求解偏差逐渐增小;3DR求解偏差逐渐增大,但都小于5%;3DR和FEM的求解精度相当。纵向比较表明:δ=2,3时,3DR比FEM的求解偏差小,说明在求解大截面变幅杆的纵向振动频率时3DR比FEM更具有求解优势。
3 大中小截面指数形变幅杆模态实验
为了验证变幅杆横向截面大小对纵向振动的影响,根据实验室的YP-5520-4Z柱型超声波换能器,设计变幅杆的工作频率为20 kHz。根据半波长圆截面指数杆的一维振动设计理论,设计了面积系数为2.9,长度为137.3 mm的三组截面不同的变幅杆。大端直径 D1分别为 58,97,116 mm;小端直径 D2分别为 20,30,40 mm,材料为45#钢。采用 MasterCAM9.0 软件对指数形变幅杆自动编程,在FTC-20数控车床上加工出的三个指数形变幅杆如下图3所示。为了使加速度传感器磁座与变幅杆充分吸合,分别在变幅杆大端、距大端截面100 mm处两周分别铣出四个小平面。
采用一点激励多点响应的锤击测试方法测试了大、中、小指数型变幅杆的第一阶弯曲扭转、纵向自由振动固有频率和振型。变幅杆的锤击脉冲激振测试系统如图4所示,实验中将变幅杆用绳子悬挂起来,以模拟自由状态。采用INV3020D数据采集仪25通道,进行1个通道激励、24个并行响应通道的频响函数测量;力锤手柄传感器一端连接到数据采集仪上,数据采集仪通过网线连接到装有DASP(Data Acquisition&Signal Processing)Coinv DASPV10.0软件的笔记本上,接线图如上图5所示。8个三维加速度传感器(型号DYTRAN3263M8),四个一组分别沿变幅杆大端、小端圆周阵列布置,通过磁座与变幅杆预先加工的小平面吸合。加速度数据连接线连接到数据采集仪上。实验时,限制采样频率的范围为1 kH~22 kHz,通过在DASPV10.0软件中输入变幅杆坐标点建立分析模型,使用力锤在距离变幅杆大端100 mm截面(振幅最大处)外侧进行多次锤击,经DASPV10.0软件读取相应数据,平均,分析处理,读取记录相应谐振频率和振型。依据扭转、纵向典型振型,确定相应的谐振频率见表5。

4 谐振频率数据对比分析
利用有限元分析软件Ansys12.0,45#钢材料特性参数弹性模量E=210 GPa,泊松比ν=0.3,纵波声速为C=5 200 m/s,密度ρ=7 800kg/m3。所选择的分析单元类型为20节点的solid95,4水平智能划分网格,扩展模态30阶,频率范围为0~30 000 Hz,所求得的变幅杆固有频率见表5。
表5中D1为指数形变幅杆大端直径,D2为变幅杆小端直径,L为变幅杆长度。f1为一维欧拉-伯努利方法求得的频率,f3为三维弹性振动能量变分原理求得的频率,fA为有限元Ansys12.0求得的频率,fT为变幅杆加工后锤击激励模态实验所测得的频率。0T表示n=0指数形变幅杆扭转振动,0L表示纵向振动;1B表示n=1指数形变幅杆弯曲振动。随着指数形变幅杆截面增大,一维振动求解理论误差越来越大,当截面尺寸接近1/2波长时,求解误差接近或超过5%;而三维振动里兹法的求解结果与Ansys12.0的求解结果水平相当;锤击激励模态实验与Ansys12.0的求解结果一致性很好,表明实验数据可靠。
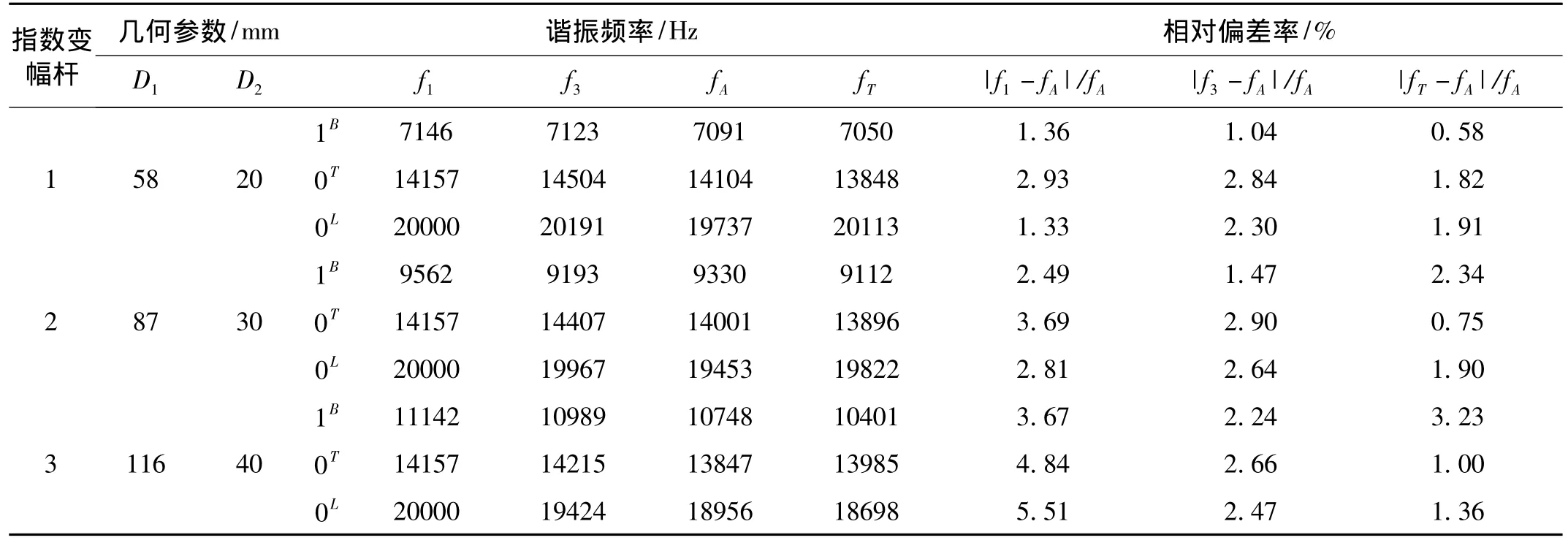
表5 大中小指数形变幅杆谐振频率不同求解理论方法的数据对比Tab.5 Comparison of the first inherent frequencies in form1DB、3DR、FEA and modal experiment methods of exponential horns with different circular cross-sections
5 结论
(1)三维弹性振动里兹法统一了非均匀圆截面变幅杆纵向、扭转、弯曲振动的频率方程求解方法,为其他截面变幅杆的振动求解提供了一种数值求解方法;
(2)推导计算了单一变幅杆的扭转、纵向、弯曲振动的无量纲圆频率。计算表明,三维弹性振动里兹法在大截面、短粗变幅杆的求解中比一维欧拉-伯努利振动求解理论更精确,与有限单元法有同样的求解精确性;
(3)在设计非均匀圆截面变幅杆时,只需要带入材料特性参数E,ρ,ν和长度参数L,即可求得谐振频率;并可方便对不同长径比、不同阶次高频变幅杆的对比研究分析,无需Ansys在分析不同对象模型时所需的重复前处理步骤;
(4)可方便形成半解析半数值求解方法,利于编程实现振动系统的参数化变型系列设计,可以提高设计效率,开发功率超声计算机辅助设计系统。
[1] Breh D E,Dow T A.Review of vibration-assisted machining[J].Precision Engineering,2008,32(3):153- 172.
[2] 贺西平,高 洁.超声变幅杆设计方法研究[J].声学技术,2006,25(1):82-86.HE Xi-ping,GAO Jie.A review of ultrasonic solid horn design[J].Technical Acoustics,2006,25(1):82-86.
[3] 吕 明,王时英,轧 刚.超声珩齿弯曲振动变幅器的位移特性[J].机械工程学报,2008,44(7):106-111.LÜ Ming, WANG Shi-ying,YA Gang. Displacement characteristics of transverse vibratory disc transformer in ultrasonic gear honing[J]. Journal of Mechanical Engineering,2008,44(7):106-111.
[4] 王时英,吕 明,轧 刚.超声珩齿指数型变幅器的动力学特性[J].机械工程学报,2007,43(6):190-193.WANG Shi-ying,LÜ Ming,YA Gang.Dynamical characteristics of exponential transformer in gear honing[J].Chinese Journal of Mechanical Engineering,2007,43(6):190-193.
[5] 张鹏利,付志强,林书玉.悬链线形超声变幅杆共振频率的瑞利修正[J].陕西师范大学学报,2009,37(5):35-37,41.ZHANG Peng-li,FU Zhi-qiang,LIN Shu-yu.Rayleigh modification on resonance frequency of catenary horn[J].Journal of Shaanxi Normal University,2009,37(5):35-37,41.
[6] Zhou G P,Li M X.A study on ultrasonic solid horns for flexural mode[J].J.Acoust.Soc.Am,2000,107(3):1358-1362.
[7] Kanga J H,Leissa A W.Three-dimensional vibration analysis of thick,tapered rods and beams with circular cross-section[J].International Journal of Mechanical Sciences,2004,46(6):929-944.
[8] Kanga J H,Leissa A W.Three-dimensional vibrations of solid cones with and without an axial circular cylindrical hole[J].International Journal of Solids and Structures,2004,41(14):3735-3746.
[9] Bayǒn A,Gascǒn F,Medina R.et al.Study of pure transverse motion in free cylinders and plates in flexural vibration by Ritz's method[J].European Journal of Mechanics A/Solids,2011,30(3):423-431.
[10] 曹志远.板壳振动理论[M].北京:中国铁道出版社,1989:4-8.
