基于SVD降噪和盲信号分离的滚动轴承故障诊断

陈恩利，张 玺，申永军，曹轩铭

(石家庄铁道大学 机械工程学院，石家庄 050043)

滚动轴承发生故障时其振动信号是一种非线性非平稳信号，并且信号微弱、调制性强、频带范围宽。传统的诊断方法，如时域分析法和频域分析法，对于诊断滚动轴承局部和早期故障，应用效果不佳。

经典的功率谱方法难以检测出信噪比较低的故障特征信号，并且对微弱的故障特征信号不敏感[1]。由于滚动轴承机械系统结构复杂，故障形式多样且呈现一定程度的非线性行为，振动信号和工作状态之间并不存在确定的函数关系。这就决定了滚动轴承故障诊断的难度和复杂性。因此，采用先进的现代信号处理技术提取滚动轴承检测信号中的故障特征信息成为近年来研究的热点。

滚动轴承故障诊断的方法有很多，如小波变换、Hibert包络解调、经验模态分解(EMD)、局部均值分解(LMD)等。蔡艳萍等[2]结合EMD信号分解方法和谱峭度，通过谱峭度来选取由轴承缺陷所引起的共振频率所在频带的MF分量，自动构建最佳包络来进行故障诊断。何田等[3]利用LMD方法将多分量的振动信号自适应地分解到一系列的PF分量，对PF的瞬时幅值进行FFT，有效地提取齿轮故障信息。李国宾等[4]针对柴油机振动信号的特点，提出应用小波包变化和奇异值分解提取振动信号特征的方法。陈亚弄等[5]对LMD算法进行了改进，并将其应用到滚动轴承三种典型故障的诊断中，结果表明LMD能够从实际轴承损伤类故障信号中分离出包含丰富故障信号的单分量信号。

奇异值分解(Singular Value Decomposition，SVD)算法具有良好的稳定性和不变性[6－7]，其分解的奇异值反映数据的内在属性，可以降低信号中的噪声，提高信噪比。盲信号分离(Blind Signal Separation，BSS)[8]是在未知源信号和传输通道参数的情况下，根据输入源信号的统计特性，仅由观测信号恢复出源信号的过程，对多种信号的混迭分离具有很强的针对性。本文将奇异值分解技术和盲信号分离技术相结合提取滚动轴承的故障特征信息。通过奇异值分解的降噪特性去除混合信号中的噪声，然后利用盲信号分离技术对去噪后的信号进行盲源分离，提取出原始的故障信号。

1 基于SVD降噪的盲信号分离故障诊断方法

将SVD和BSS结合应用于滚动轴承故障信号的检测中，其研究思路来源于两种方法的各自优点。奇异值分解方法可以降低实测振动信号噪声，提高信噪比，突出振动信号的故障特征。假设滚动轴承某通道测试的振动信号为 x=[x1，x2，x3，…，xN]，则用奇异值分解方法重构的吸引子轨迹矩阵为:

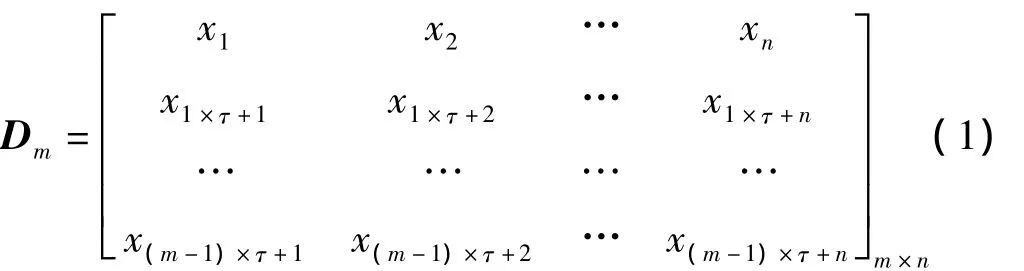
式中:τ为延迟步长;m为嵌入维数;n=N－(m－1)×τ。

用奇异值分解技术实现信号降噪，成功的关键在于Dm的构造，重构相空间时，参数的选择直接影响结构。由式(1)看出，决定Dm的主要参数是延迟步长τ。本文采用自相关函数法计算嵌入维数，具体方法是，计算原振动信号时间序列 x=[x1，x2，x3，…，xN]的自相关函数rk，τ取使得rk小于某个域值(一般取0.1)的最小k值。

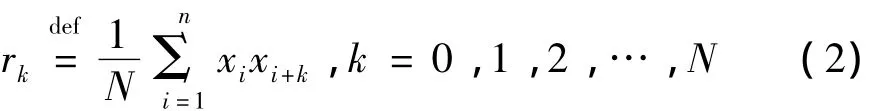
滚动轴承发生故障时会产生冲击和不同程度的调制现象，故障信号通常为调制信号[9]，而调制信号对应的奇异值主要分布在0～kw(kw＜n)阶(kw为调制信号的重构吸引子轨迹矩阵的秩)。

矩阵Dm的构造是奇异值分解技术的关键。首先计算原时间序列的延迟步长，利用计算的τ对时间序列做n维相空间重构，再对重构矩阵中的时间序列进行傅里叶变换，接着对变换后的重构矩阵进行奇异值分解，此时分解后的奇异值经过傅里叶变换克服了对噪声敏感的缺点，然后找出故障信号对应的奇异值，其它置零，构造新的特征矩阵，利用此矩阵进行反奇异值计算得到降噪后的故障信号。

在滚动轴承实际故障信号采集中，由于传感器通常布置在轴承座或机壳上，使采集的信号包含转子和滚动轴承的状态信息，当轴承存在多种故障时，采集的信号往往是多种故障的混合信号，这就使故障诊断变得困难。盲信号分离是通过构造分离矩阵B，将多个观测信号按照统计独立的原则分解为若干个独立信号，从而实现信号的分离。

盲信号分离的核心问题是求解分离矩阵B使得输出序列y(t)=B·x(t)=B·A·s(t)。目前对于分离矩阵B和分离信号的求解基于两种方法:独立分量分析ICA和非线性主分量分析Nonlinear-PCA。本文采用基于矩阵联合对角化的预白化JADE算法。JADE算法的基本思路是，在球化数据z的基础上，根据选择的权重矩阵M计算相应的四阶累积量Qz(MI)，最终寻求能使各个Qz(MI)联合对角化的矩阵V。具体步骤如下:

(1)求球化矩阵W，使得z=Wx球化。

(2)对所有选取的权重矩阵Mi∈M，求出球化数据z的四阶累积量Qz(MI)，i=1～p。

其中:Qz(MI)是N×N阶矩阵，其定义如下:

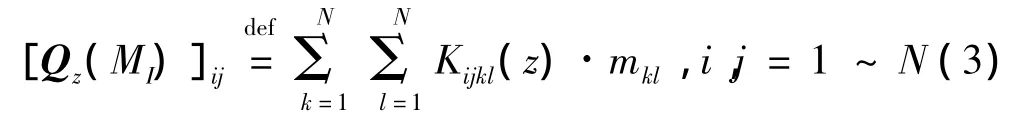
式中:Mi为预先设定的p×q阶矩阵，Kijkl(z)是矢量z中第 i，j，k，l四个分量的四阶累积量，mkl是矩阵 Mi的第 k，l元素。

(3)通过优化步骤求V，使得各Qz(MI)联合对角化，即:使式(4)取极小值。

(4)得到分离矩阵B及分离结果y:

关于权重矩阵Mi的选择可参考有关文献。

本文在现有研究的基础上，提出了一种基于SVD降噪的盲信号分离故障诊断新方法，通过奇异值分解的降噪特性去除混合信号中的噪声，对去噪后的信号进行盲源分离，分析各分离信号的频谱图，提取故障特征频率从而识别故障部位。

2 实验研究

为了验证该方法的有效性，将该方法用到滚动轴承实测故障信号中。实验在铁路货车轮对滚动轴承故障诊断实验台架上完成。实验台架主要组成部分有:机架和液压轮对夹紧装置、调速驱动电机及液压与电气控制装置，如图1所示。采用的轮对型号是RD2型。轴承的型号是352226X2－2RZ型和197726型，二者除内部密封装置外，结构尺寸大致相同，适用于K2、K3、K4等快速转向架。轮对和滚动轴承之间为过盈压装配合。

图1 铁路货车轮对滚动轴承故障诊断实验台Fig.1 Test rig of railway wagons bearings fault diagnosis

实验所用故障轴承为车辆厂提供的厂修检查发现的故障轴承，其典型故障为外圈故障(如图2所示)、滚动体故障(如图3所示)同时分别选用与RD2型轮对相匹配的正常状态轴承。实验选用的振动传感器为CA－YD－186型加速度传感器，分别安装在轮对滚动轴承右端轴承座和支架上，其中轴承支座水平方向设置一个传感器，垂直方向设置两个传感器，支架水平和垂直两个方向各设置一个传感器。其传感器布置图见图4所示。5个通道的振动加速度信号通过KD5007型电荷放大器和INV36DF型智能信号采集仪采集得到。

表1列出了352226X2－2RZ型和197726型的主要技术参数。文献[10]给出了轴承不同故障特征频率的计算方法。其中，外圈故障特征频率:

滚动体故障特征频率:

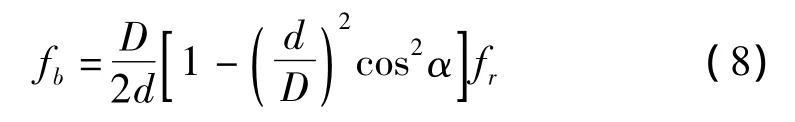
表2列出了轴承故障实验工况。从表2中看出，外圈故障特征频率f0=67.327 Hz，滚动体故障特征频率fb=27.314 Hz。

表1 352226X2－2RZ型轴承的主要技术参数Tab.1 Major technical parameters for bearing of 352226X2－2RZ

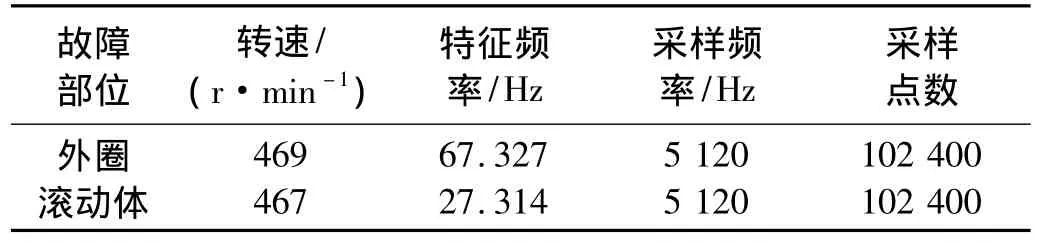
表2 轴承故障实验工矿明细Tab.2 Bearing test data

图2 外圈剥离故障Fig.2 Bearing out-ring stripping faults

图3 滚动体表面损伤故障Fig.3 Bearing clement surfaces damage faults

图4 传感器布置图Fig.4 Sensor placement

3 基于SVD降噪的盲信号分离滚动轴承故障特征提取

3.1 外圈剥离故障分析

在实验台的右轴承座上换上外圈剥离的故障轴承，在轮对转速为469 r/min下采集的振动信号频谱曲线如图5所示，图6所示为Hilbert变换包络解调谱，可见由于受噪声的影响，两幅图中都看不出明显的故障特征，需要进一步降噪处理。

用基于频域的奇异值分解技术对该实测振动信号进行分析。首先对测试信号进行傅里叶变换，计算其自相关函数，确定最小延迟步长，自相关函数图形如图7所示。由图可知，最小延迟步长为2。根据已选定的延迟步长τ，对经傅里叶变换后的振动信号进行奇异值分解，选取实验点数1 024，嵌入维数60。图8为实测信号吸引子矩阵的奇异值分布图。由图可知，故障信号对应的奇异值分布在2到7阶。

通过分析最终选定与故障信号相对应的奇异值，其它置零进行重构，重构信号的频谱曲线如图9所示，与图5比较可以看出，频谱曲线中的噪声成分明显减小。图10为频谱曲线的局部放大图，可以看出在频率68.13 Hz、135.6 Hz、201.3 Hz、271.3 Hz、338.8 Hz、406.3 Hz处有谱峰存在，这些频率与计算得出的轴承外圈故障特征频率f0=67.327 Hz及其2倍频134.65 Hz、3倍频201.98 Hz、4倍频269.31 Hz、5倍频336.64 Hz、6倍频403.96 Hz基本吻合。

本实验采集的振动信号含有大量噪声，主要原因是由于实验时电机直接驱动轮对转动，使采集的振动信号频率可能包含电机转动的固有频率和支架自身振动的固有频率。图11原始信号的频谱曲线，图12、图13为经过SVD降噪处理的1、2、3通道信号的时域曲线和频谱曲线。利用上节提出的JADE法对经过SVD降噪后的实测信号进行盲源分离，其分离后信号的频谱图如图14所示。

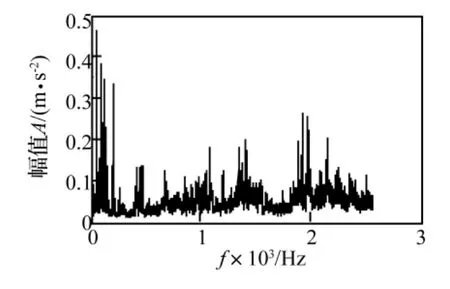
图5 外圈剥离轴承振动信号的频谱曲线Fig.5 Frequency spectrum of vibration signal in bearing out-ring stripping faults

图6 Hilbert变换包络解调谱Fig.6 Hilbert transform envelope spectrum

图7 外圈剥离轴承振动信号延迟步长Fig.7 Delay step of vibration signal in bearing outer ring stripping fault

图8 外圈剥离轴承振动信号的奇异值分布Fig.8 Singular value distribution of vibration signal in bearing outer ring stripping fault

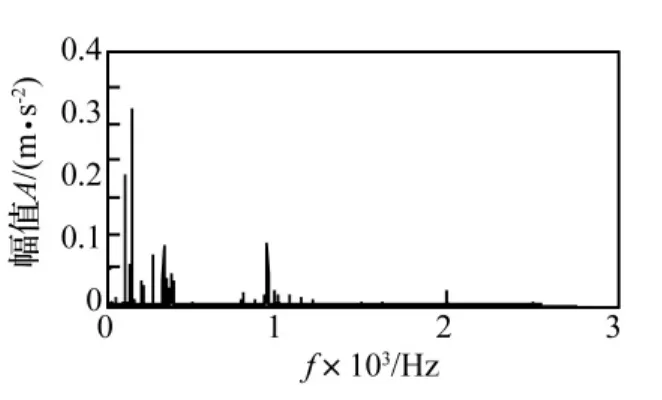
图9 外圈剥离轴承重构信号频谱曲线Fig.9 Frequency spectrum of reconstruction signal in bearing outer ring stripping fault

图10 外圈剥离轴承重构信号局部放大图Fig.10 Partial enlargement frequency spectrum of reconstruction signal in bearing outer ring stripping fault

图11 外圈剥离轴承原始信号频谱曲线Fig.11 Frequency spectrum of original vibration signal in bearing outer ring stripping fault

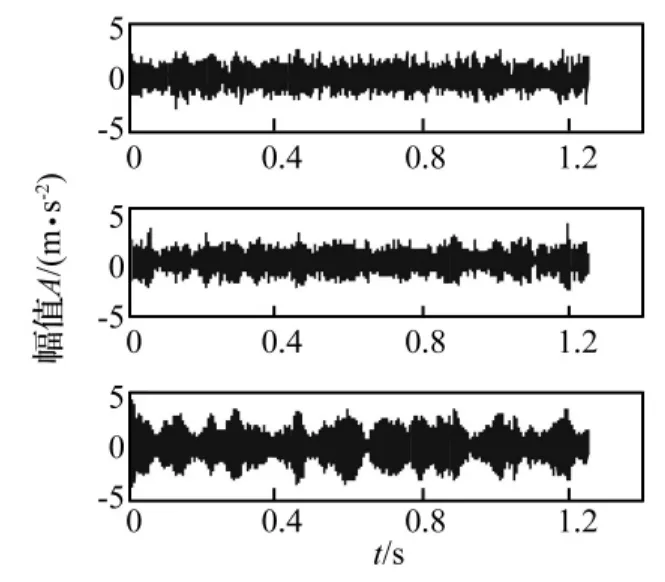
图12 外圈剥离轴承降噪信号时域曲线Fig.12 Time domain curves of denoiser signal in bearing outer ring stripping fault

图13 外圈剥离轴承降噪信号频谱曲线Fig.13 Frequency spectrum of denoiser signal in bearing outer ring stripping fault

表3 外圈剥离轴承分离信号频率和外圈故障特征频率Tab.3 Frequency of separation signal and fault features in bearing outer ring stripping fault

当轴承外圈故障时，滚动体通过故障部位会产生频率为 nf0(n=1，2，…)的冲击振动，在 nf0(n=1，2，…)处有谱峰存在。从图14中可以看出，在频率135.6 Hz、338.8 Hz、811.9 Hz、946.9 Hz、1152 Hz、1419 Hz 处有明显的谱峰存在，这些频率与通过式(8)计算得出的理论的轴承外圈故障特征频率 f0=67.327 Hz及其2倍频 134.65 Hz、5 倍频 336.6 Hz、12 倍频 807.9 Hz、14倍频942.6 Hz、17 倍频 1144.6 Hz、21 倍频 1413.9 Hz基本吻合，如表3所示。显然，经过盲信号分离后，滚动轴承的外圈故障特征能够更加明显的体现。

3.2 滚动体表面损伤故障分析

在实验台的右轴承座上换上滚动体表面损伤的故障轴承，在轮对转速为467 r/min下采集的1通道、2通道、3通道振动信号频谱曲线如图15所示。用基于频域的奇异值分解技术对三个通道的原始信号进行降噪处理，重构信号的频谱曲线如图16所示，与图15比较可以看出，频谱曲线中的噪声成分明显减小。

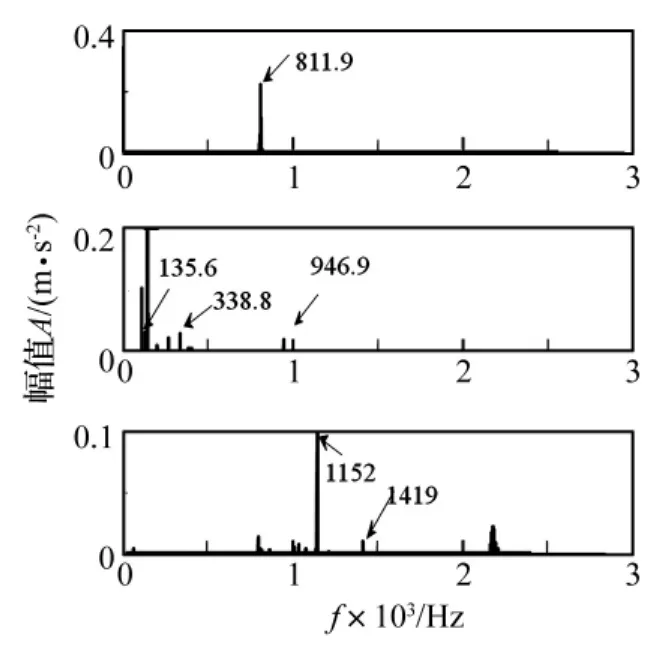
图14 外圈剥离轴承分离信号的频谱曲线Fig.14 Frequency spectrum of separation signal in bearing outer ring stripping fault

图15 滚动体表面损伤轴承原始信号频谱曲线Fig.15 Frequency spectrum of original vibration signal in bearing clement surfaces damage faults

图16 滚动体表面损伤轴承降噪信号频谱曲线Fig.16 Frequency spectrum of denoiser signal in bearing clement surfaces damage faults

利用JADE法对经过SVD降噪后的实测信号进行盲源分离，其分离后信号的频谱图如图17所示。

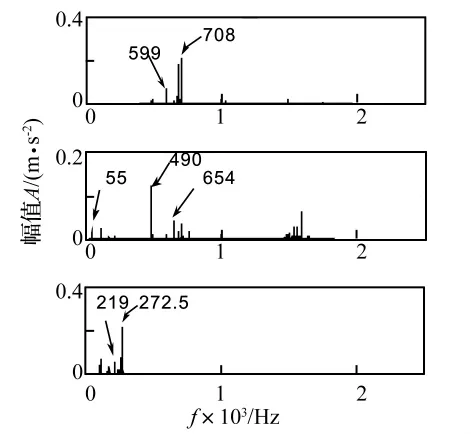
图17 滚动体表面损伤轴承分离信号频谱曲线Fig.17 Frequency spectrum of separation signal in bearing outer ring stripping fault

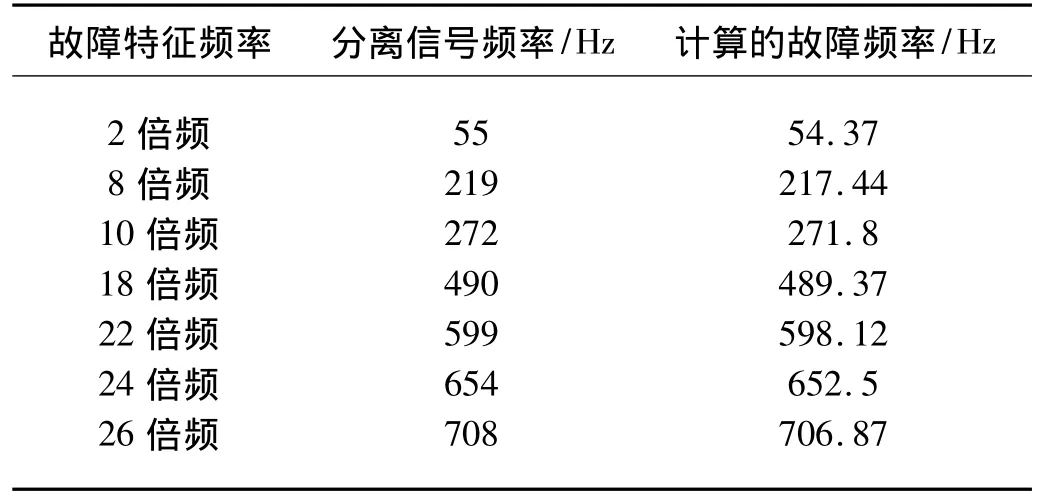
表4 滚动体表面损伤轴承分离信号频率和滚动体故障特征频率Tab.4 Frequency of separation signal and fault features in bearing clement surfaces damage fault

当滚动体有损伤时，损伤部位通过内圈或外圈滚道表面时会产生频率为nfb(n=1，2，…)冲击性振动。由于滚动轴承通常都存在径向间隙，使振动受到滚动体公转频率fc的调制，振动频率为nfb±fc(n=1，2，…)。

从图 14 中可以看出，在频率 55 Hz、219 Hz、272.5 Hz、490 Hz、599 Hz、654 Hz、708 Hz 处有明显的谱峰存在，这些频率与通过式(9)计算得出的理论的轴承外圈故障特征频率f0=27.18 Hz及其2倍频54.37 Hz、8倍频 217.44 Hz、10 倍频 271.8 Hz、18 倍频 489.37 Hz、22倍频598.12 Hz、24 倍频652.5 Hz、26 倍频 706.87 Hz基本吻合，如表4所示。显然，经过盲信号分离后，滚动轴承的滚动体故障特征能够更加明显的体现。

4 结论

本文针对轴承故障振动检测信号中含有强干扰噪声的特点，提出了基于SVD降噪的盲信号分离方法。通过利用奇异值分解的降噪特性去除混合信号中的噪声，利用盲信号分离技术对去噪后的信号进行盲源分离，提取出原始故障信号。通过滚动轴承台架实验提取外圈故障轴承和滚动体故障轴承的振动信号，利用本文方法进行了验证，结果表明了本方法的正确性和有效性。

[1]王艳芳.齿轮箱故障特征提取技术研究[D].太原:中北大学，2007.WANG Yan-fang.Study of technology of feature extraction of gearbox fault[D].Taiyuan:North University of China，2007.

[2]蔡艳平，李艾华，石林锁，等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击，2011，30(2):167－172.CAI Yan-ping，LI Ai-hua，SHI Lin-suo et al.Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J].Journal of Vibration and Shock，2011，30(2):167 －172.

[3]何 田，林意洲，郜普刚，等.局部均值分解在齿轮故障诊断中的应用研究[J].振动与冲击，2011，30(6):196－201.HE Tian，LIN Yi-zhou，GAO Pu-gang，et al.Application of local mean decomposition in gear fault diagnosis[J].Journal of Vibration and Shock，2011，30(6):196 －201.

[4]李国宾，关德林，李廷举.基于小波包变换和奇异值分解的柴油机振动信号特征提取研究[J].振动与冲击，2011，30(8):149－152.LI Guo-bin，GUAN De-lin，LI Ting-ju.Feature extraction of diesel enginevibration signalbased on waveletpacket transform and singularity value decomposition[J].Journal of Vibration and Shock，2011，30(8):149 －152.

[5]陈亚农，郜普刚，何 田，等.局部均值分解在滚动轴承故障综合诊断中的应用[J].振动与冲击，2012，31(3):73－78.CHEN Ya-nong，GAO Pu-gong，HE Tian，et al.Roller bearing comprehensive fault diagnosis based on LMD[J].Journal of Vibration and Shock，2012，31(3):73 －78.

[6]Press W H，Flannery B P，Teukolsky S A，et al.Numerical recipes:the art of scientific computing[M]，New York:the Press Syndicate of the Univ.of combridge，1986.

[7]Golub G H，Van Loan C F.Matrix computation[M].Baltimore:Johns Hopkins University Press，1983.

[8]张贤达，保 铮.盲信号分离[J].电子学报，2001，29(12):1766－1771.ZHANG Xian-da，BAO Zheng.Blind Source Separation[J].Chinese Journal of Electronics，2001，29(12):1766 －1771.

[9]陈恩利，吴勇军，申永军.基于改进奇异值分解技术的齿轮调制故障特征提取[J].振动工程学报，2008，21(5):530－534.CHEN En-li，WU Yong-jun，SHEN Yong-jun.An improved method of detecting modulated gear fault characteristic based on singularity value decomposition[J].Journal of Vibration Engineering，2008，21(5):530 －534.

[10]梅宏斌.滚动轴承振动监测与诊断[M].北京:机械工业出版社，1996.