智能弹簧装置减振性能的影响因素分析

倪 德，朱如鹏

(南京航空航天大学 江苏省精密与微细制造技术重点实验室，南京 210016)

智能弹簧通过外加控制电压驱动压电陶瓷作动器动作而产生微位移，改变系统结构参数，如阻尼和刚度，间接地抑制振动位移或反作用力的传递。与直接抑制激振力的方式相比，它不需要复杂的位移放大装置，也不需要很高的驱动电压，结构简单，更易于实现。因此，基于智能弹簧概念的减振技术具有良好的应用前景和研究价值。南京航空航天大学的陈勇，卡尔顿大学的Nitzsche，加拿大国家研究委员会航空研究协会Zimcik和Wickramasinghe等针对直升机旋翼转子的扭转振动，做了大量工作，建立了智能弹簧减振的数值仿真模型，通过台架试验和风洞试验验证了智能弹簧的减振性能和环境适应能力，并开发了自适应控制算法，算法先后在MATLAB xPC平台和DSP平台上实现[1－7]。Daley 等[8－9]研究了某智能弹簧支撑系统周期振动抑制的反复控制方法，通过仿真和试验对智能弹簧的减振性能进行了研究。Aldemir等[10]提出一种基于智能弹簧装置的半主动减振技术，使旋转机械能安全跨越临界转速，利用基于遗传算法的优化技术确定智能弹簧装置的最佳设计参数。本文通过数值仿真的方法，研究了智能弹簧控制参数、智能弹簧结构参数和滑动摩擦力速度影响系数对旋转机械减振性能的影响，得到了一些探索性的结论。

1 智能弹簧减振原理

智能弹簧减振的原理图，如图1所示。

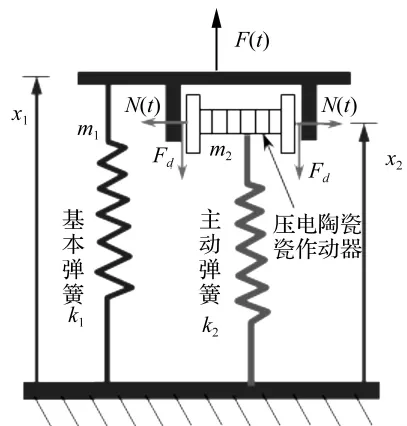
图1 智能弹簧减振原理图Fig.1 Smart Spring vibration suppression concept

如图1，智能弹簧结构由基本弹簧k1、主动弹簧 k2和压电陶瓷作动器等组成。两弹簧平行布置，构成两条载荷传递路径，其粘性阻尼系数分别为c1和c2，质量为m1和 m2。结构一端与基础相连，另一端承受激振力F(t)。压电陶瓷作动器与主动弹簧固接，放置在与振动结构之间可以相对滑动的套筒内。未加控制电压时，压电陶瓷作动器可在垂直方向自由移动，主动弹簧k2不起作用，振动载荷完全由基本弹簧k1承受，系统振幅最大。当在压电陶瓷上施加控制电压时，压电陶瓷作动器沿水平方向产生微位移s。当s大于振动结构与套筒间的初始间隙σ后，作动器将在振动结构上作用一法向力N(t)，即作动力，随着系统的运动，在两者之间形成一个动摩擦力Fd，使得主动弹簧在振动系统中起作用，与基本弹簧一起承受振动载荷，系统动刚度变大，振幅减小。若动摩擦力足够大，基本弹簧和主动弹簧完全耦合，二者刚性联结成一单自由度系统，系统振幅最小。

2 旋转机械振动控制状态方程的建立

2.1 研究对象的力学模型

旋转部件偏心质量引起的离心力是旋转机械主要的激振力之一[11]。图2为一旋转机械垂直方向的横向振动力学模型。图中M为旋转机械的总质量，m为转子的偏心质量，e为偏心距，坐标x表示非旋转部分质量M－m在垂直方向的横向振动位移。设转子的转角、角速度、角加速度分别为φ，ω，α;初始转角和角速度为φs0，ωs0。忽略重力影响，系统的运动微分方程可表示为:

式(1)右边为转子偏心质量在垂直方向所产生的简谐激振力分量。当系统等加速运行时，激振力F(t)=me(ω2sinφ－αcosφ)，其中ω=ωs0+αt，φ =φs0+ωs0t+αt2/2;系统等速运行时，F(t)=meω2sinωt，此时 ω 为常数。

对于旋转机械，智能弹簧可安装在支承与基础之间的载荷传递路径中，通过改变系统的有效支承刚度和阻尼等结构参数，改变系统的传递特性，减小系统的振幅或振动力。建立基于智能弹簧的旋转机械减振力学模型如图3所示。

图2 旋转机械横向振动力学模型Fig.2 Lateral vibration mechanical model of rotating machine

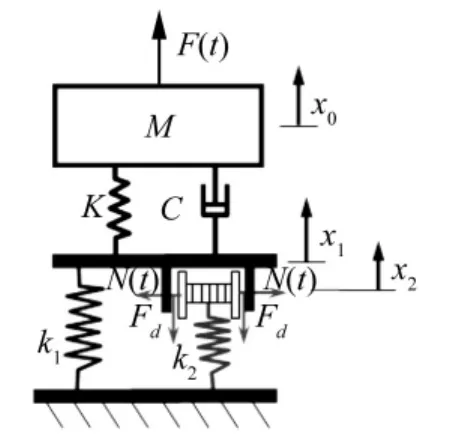
图3 基于智能弹簧的旋转机械减振力学模Fig.3 Vibration suppression mechanical model of rotating machine based on smart spring

2.2 研究对象的振动控制状态方程

如图3，系统的振动运动微分方程组为:

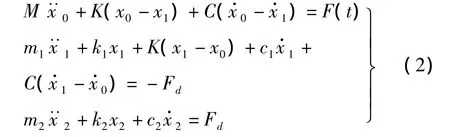
其中:

系统等加速运行时:

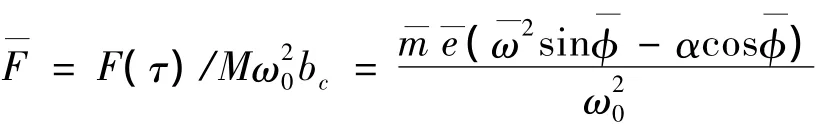
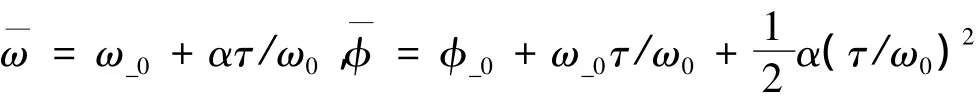
系统等速运行时:Ω =ω/ω0，

由式(3)得到控制系统的状态空间表达式为:

其中:

2.3 研究对象的滑动摩擦力

图4 滑动摩擦系数随相对滑动速度变化曲线Fig.4 Sliding friction coefficient curve vs.relative speed

滑动摩擦力可简化为一干摩擦阻尼模型，摩擦材料为钢－钢。滑动摩擦系数μ(t)的变化过程很复杂，其大小为:μdmin＜μ(t)＜ μsmax，μdmin为最小动摩擦系数，μsmax为最大静摩擦系数。影响 μ(t)的因素有很多，对于本文的研究对象，相对滑动速度vr为主要影响因素。当 vr较小时，μ(t)随|vr|增大而减小;当相对滑动速度|vr|等于某一特定值vrs时，滑动摩擦系数μ(t)取得最小值;当|vr|＞vrs时，滑动表面因温升而粘结，μ(t)将随|vr|增大而增大[12－13]。μ(t)随|vr|变化的曲线如图4 所示。

滑动摩擦系数可表征为相对滑动速度的多项式函数，目前常用的干摩擦阻尼模型为[13]:

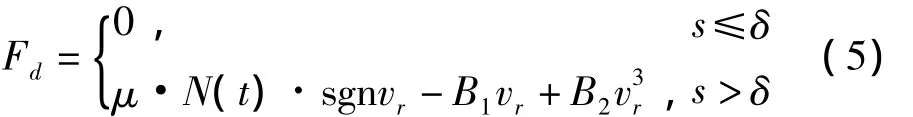
3 仿真与分析

3.1 智能弹簧控制参数－压电陶瓷作动力对减振性能的影响

本文在MATLAB/Simulink环境中对式(4)进行仿真分析，仿真参数如表1所示。

图5为转速n=0时，旋转机械的单位阶跃响应，作动力为0时，最大振幅为5.2×10－6m。作动力可通过外加电压进行控制，其对系统最大振幅的影响如表2所示。

表2 作动力对系统幅值响应的影响Tab.2 Influence of actuation force on response of system

其中:

表2的结果表明，增大作动力，滑动摩擦力Fd增大，系统的阻尼比增大，提高了系统的动刚度，系统的振幅减小，减振性能增强。增大作动力虽然可以提高系统阻尼比，但系统的阻尼比不会随着作动力增大而无限增大下去。大约在N(t)=6.4 N时，系统的阻尼比取得最大值。若继续增大作动力，系统响应幅值回升，即系统阻尼比减小。实际情况中，系统响应曲线的平衡位置应向下平移。因为当作动力达到一定值后，基本弹簧与主动弹簧逐渐耦合在一起，系统的静刚度增大，使得系统固有频率增大，而阻尼比逐渐减小(能量耗散能力降低)[4]。当N(t)≥25 N时，干摩擦力相对于激励强度过分大，滑动表面被粘住，两个弹簧刚性耦合在一起，因而它不再耗散能量，此时系统的静刚度值最大，振幅最小。

随着作动力的增大，系统固有频率维持不变的区间，系统的静刚度一定，阻尼比增大，属于阻尼控制;而系统固有频率变化的区间，系统静刚度增大，阻尼比减小，属于刚度控制。

图6为旋转机械稳定工作在n=4 500 r/min时，系统的时域响应曲线图。图6(a)说明，对于阻尼控制方式，随着作动力的增大，系统的最大振幅有所减小，且稳定时间逐渐缩短，但稳定阶段振幅变化不大，减振效果不理想。对于刚度控制方式，当N(t)≥2 600 N时，基本弹簧与主动弹簧刚性耦合在一起，系统响应幅值最小，振幅峰值减小了85.72%，减振效果十分明显，如图6(b)。因此，对于恒转速运行的强迫振动系统，适宜于采用刚度控制方式

图5 旋转机械单位阶跃响应曲线(n=0 r/min)Fig.5 Dynamic response of rotating machine due to a step

图6 旋转机械恒转速运行时的时域响应图(n=4 500 r/min)Fig.6 Time domain responses of rotating machine during the constant rotation

图7 为2 s内，旋转机械以360 rad/s从0 r/min等加速到4 500 r/min的整个过程，系统的瞬态响应曲线图，系统在t≈0.93 s时越过临界转速。图7(a)为阻尼控制方式下，作动力大小对系统响应的影响。图示表明，在共振区域附近，减振效果最为明显，且作动力越大，减振效果越好;图7(b)为系统无控制与刚度控制(两弹簧刚性耦合)两种情况下的瞬态响应曲线对比图，在刚度控制情况下，智能弹簧结构由两个自由度刚性联接成为一个自由度，系统的临界转速由于系统的静刚度增大而提高，从而避开了原来的临界转速，振幅大幅度减小。值得注意的是，有时如果设计不合理，可能会在工作转速附近激发了新的共振点，因此要注意选择合适的参数。

为了使旋转机械能够安全地跨越临界转速，比较有效的实现方法有:

(1)根据系统的运行状况，自适应地选择合适的外加电压调节作动力，通过增大系统阻尼比的方式提高系统的动刚度，减小系统的振幅，使得系统安全地跨越临界转速。

(2)将主动弹簧作为系统的一个可变刚度部件，采用Bang-Bang控制决定主动弹簧是否在系统中起作用，在适当的时机改变系统的静刚度，从而避开系统的临界转速，防止发生共振。该方法要求相邻共振点的距离满足一定的要求。

3.2 智能弹簧结构参数对减振性能的影响

图8为基本弹簧结构参数对旋转机械减振性能的影响。改变基本弹簧的刚度和质量将改变系统的固有频率，系统临界转速在一定区间内浮动。如图8(a)所示，Ω=0.5时，系统临界转速区间跨越旋转机械的工作转速，刚度比g1较小时，随着g1的增大，旋转机械的减振性能逐渐减弱，当g1大于某值时，减振性能随着g1的增大逐渐增强。而当Ω=1.6与Ω=2时，系统临界转速区间不涵盖旋转机械的工作转速，减振性能将随g1的增大而逐渐增强，呈单调函数。在实际工程设计中，应把刚度比g1限制在一定范围内，既可以达到保护结构的目的，又可以获得比较好的减振性能。由图8(b)可知，随着阻尼比ζ10的增大，旋转机械的减振性能逐渐增强，且工作转速越低，效果越明显。

图7 旋转机械等加速过临界的瞬态响应曲线(n=0→4 500 r/min)Fig.7 Output responses of rotating machine during the transient rotation

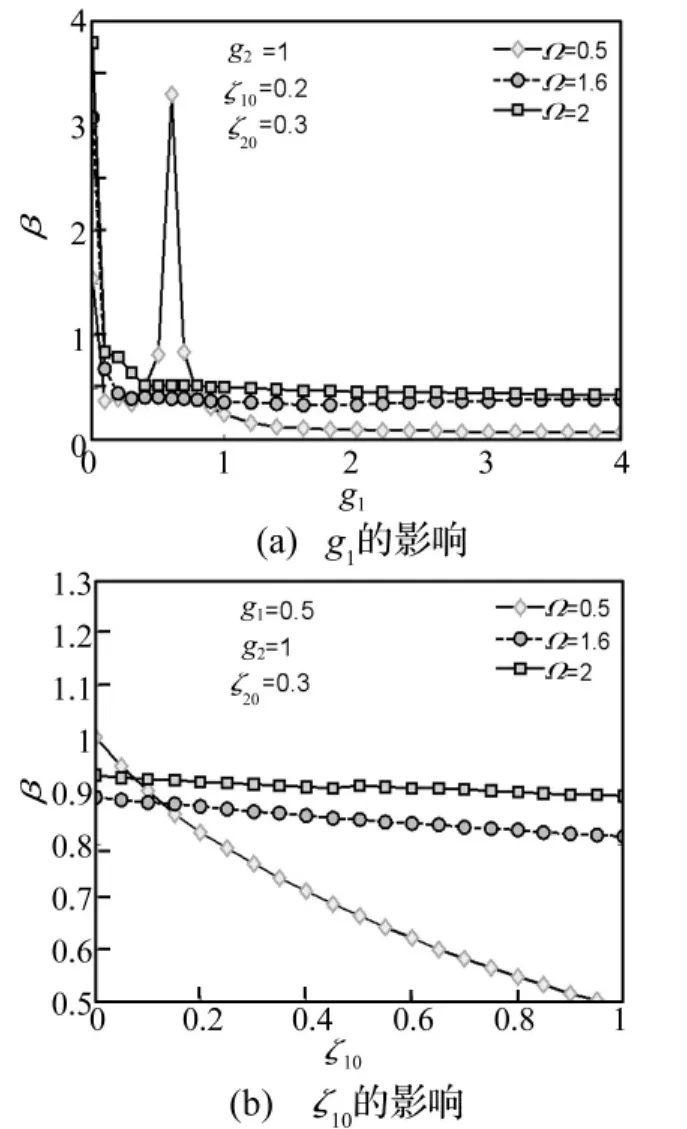
图8 基本弹簧结构参数对减振性能的影响Fig.8 Influence of primary spring structure parameters on vibration suppression performance

图9 主动弹簧结构参数对减振性能的影响Fig.9 Influence of active spring structure parameters on vibration suppression performance

主动弹簧结构参数对减振比β的影响规律如图9所示。主动弹簧通过压电陶瓷的动作间接参与到振动系统中的，不影响系统的临界转速。图9(a)表明，减振比β先随着刚度比g2的增大而减弱，当g2大于某值时，又随g2逐渐增强，且工作转速较低时，变化要明显一些。图9(b)表明，阻尼比ζ20对旋转机械减振性能的影响非常小，基本可忽略不计。

3.3 滑动摩擦力速度影响系数的影响

前面的分析没有考虑速度影响系数B1，B2的影响。取表1的仿真参数，得到系数B1，B2对减振性能的影响趋势如图10所示。由图10可知，系统响应幅值越小，相对滑动速度vr越小，B1，B2对减振性能的影响越小，经过大量的分析发现，当系统响应幅值小于10－3时，可以忽略B1，B2的影响，直接按 Coulomb干摩擦模型计算;当系统的相对滑动速度vr较大，且B1，B2较大时，需考虑其影响，而不能直接按Coulomb干摩擦模型计算，如图10的响应峰值附近区域。

图10 速度影响系数的影响Fig.10 Influence of speed influence coefficient

4 结论

(1)旋转机械在不同的运行工况下，随着作动力的增大，系统的振幅逐渐减小，减振性能增强。在作动力逐渐增大的过程中，可实现阻尼控制和刚度控制两种控制方式。当作动力取得足够大，两弹簧刚性联接后，振幅取得最小值，继续增大作动力，对振幅没有影响。对于恒转速运行的旋转机械，刚度控制方式要明显优于阻尼控制方式。对于跨临界的旋转机械，刚度控制和阻尼控制都具有良好的减振性能，但阻尼控制对控制电压的要求更低。若对控制对象的振动情况实时监控，根据使用需求，采用合适的算法，实时调整压电陶瓷作动器的驱动电压，以自适应的方式改变系统刚度与阻尼，将取得更好的减振性能。

(2)智能弹簧的基本弹簧结构参数对减振性能影响明显，同时工作转速的大小会改变其影响的变化规律。将基本弹簧刚度限制在一定范围内，随着刚度的增大，减振性能逐渐增强;增大基本弹簧的阻尼系数，也可以提高减振性能。相对于基本弹簧，主动弹簧的结构参数对减振性能的影响较小，特别是主动弹簧的内部阻尼，其影响基本可以忽略不计。因此，在实际工程应用中，应根据具体的需求，合理选用智能弹簧结构参数。

(3)相对滑动速度vr越大，系数B1，B2对智能弹簧装置减振性能的影响越大，反之越小。

[1]陈 勇，Zimcik D G，Wickramasinghe V K，et al.用于直升机振动控制的主动调谐式吸振器研究(英文)[J].Chinese Journal of Aeronautics，2003，16(4):203 －211.

[2]Wickramasinghe V K，Zimcik D G，Chen Y，et al.Smart Spring-An actively tunable vibration absorber designed to control aeroelastic response[J].Structural Dynamics and Materials Conference，2003，5:3651 －3658.

[3]Wickramasinghe V K，Chen Y，Zimcik D G，et al.Smart spring:a novel adaptive impedance control approach for active vibration suppression applications[J].Proceedings of the SPIE-The International Society for Optical Engineering，2004，5390(1):359－369.

[4]Chen Y，Wickramasinghe V K，Zimcik D G.A novel smart spring concept for helicopter blade vibration and noise suppression[J].Materials Science Forum，2005，475 －479(3):2095－2098.

[5]Chen Y，Wickramasinghe V K，Zimcik D G.Smart spring impedance control algorithm for helicopter blade harmonic vibration suppression[J].Journal of Vibration and Control，2005，11(4):543 －560.

[6]Chen Y，Wickramasinghe V K，Zimcik D G.Experimental evaluation ofthe smartspring forhelicoptervibration suppression through blade root impedance control[J].Smart Materials and Structures，2005，14(5):1066 －1074.

[7]Wickramasinghe V K，Chen Y，Zimzik D G.Experimental evaluation of the smart spring impedance control approach for adaptive vibration suppression[J].Journal of Intelligent Material Systems and Structures，2008，19(2):171 －179.

[8]Daley S，H t nen J，Owens D H.Active vibration isolation in a“Smart Spring”mount using a repetitive control approach[J].Control Engineering Practice，2006，14(9):991－997.

[9]Daley S，Zazas I，Hatonen J.Harmonic control of a‘smart spring’machinery vibration isolation system[J].Proceedings of the Institution of Mechanical Engineers，Part M，2008，222(M2):109－119.

[10]Cavalini A A，Galavotti T V，Morais T S，et al.Vibration attenuation in rotating machines using smart spring mechanism[C]//Marcelo Messias. Mathematical Problems in Engineering，New York:Hindawi Publishing Corporation，2011:328－336.

[11]胡海岩，孙久厚，陈怀海.机械振动与冲击[M].北京:航空工业出版社，2002.

[12]刘亚民.摩擦力与摩擦系数的几点性质[J].呼伦贝尔学院学报，2006，14(4):67－68，54.

[13]白鸿柏，张培林，黄协清.摩擦系数随速度变化振动系统Fourier级数计算方法研究[J].机械科学与技术，2000，19(5):745 －746，749.

[14]戴雄杰.摩擦学基础[M].上海:上海科学技术出版社，1984.