基于ITD改进算法和关联维数的转子故障诊断方法

杨 宇，王欢欢，喻镇涛，袁 辉

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082;2.东风汽车公司 技术中心试验部，襄阳 441004)

转子系统振动信号往往会呈现一定程度的非线性特征，当转子发生故障时，其振动信号会混有能量较大的与转速有关的背景信号和噪声，传统的时域或频域方法很难从这样的转子振动信号中有效提取故障信息[1]，而分形理论中的分形维数作为定量刻画混沌吸引子的一个重要参数，在研究非线性系统方面具有独特的优势。其中关联维数计算简单，便于从数据序列中直接测定，因而应用广泛，并已应用于机械故障诊断之中[2]，故可以用来提取转子系统的故障特征。相关研究表明，关联维数在较大噪声水平下难以用关联维数来准确刻画系统的工作状态和故障类型[3]，因此要提高计算精度就必须对信号进行降噪处理;而当信号的非线性特性突出时，利用线性滤波等传统方法进行降噪的效果并不明显[4]。采用 EMD(Empirical Mode Decomposition) 方 法[5]和 LMD (Local Mean Decomposition)方法[6]都可以实现对振动信号的自适应滤波，但这两种方法在理论上都还存在一些问题，如EMD的过包络、欠包络和频率混淆问题，LMD也存在由于解调而引起的信号突变的问题。目前这些问题仍在研究当中[7]。为了降低转子振动信号的噪声，本文采用内禀时间尺度分解(ITD)改进算法对转子振动信号进行分解以达到降噪的目的。

ITD方法是由Frei提出的另一种自适应时频分析方法[8]，该方法自适应地将非平稳信号分解成为若干瞬时频率具有物理意义的单分量信号(固有旋转分量)。文献[8]虽然将ITD方法和EMD方法进行了对比，分析了ITD方法在端点效应和计算速度上的优势，但是并没有对ITD方法及固有旋转分量的物理意义进行阐述。因此本文在阐述ITD方法及其固有旋转分量的物理意义的基础上，提出了基于ITD的改进算法，并利用ITD改进方法对转子振动信号进行分解，将包含主要故障信息的若干分量进行组合作为降噪后的转子振动信号，并对降噪前后转子系统5种状态下的信号分别计算了关联维数，对比发现，降噪后的关联维数区分性明显增强，因此可以用该方法识别转子的工作状态和故障类型。

1 ITD改进方法

1.1 ITD方法

ITD方法将待分析的非平稳信号分解成一系列的固有旋转分量和一个单调的趋势信号。设Xt是待分析的原信号，分解前先定义一个基线提取算子L，使得从原始信号中去掉该基线后剩下的余量信号成为一个固有旋转分量。一次分解的表达式为[8]:

式中假设在[0，τk]上定义了 Lt和 Ht，而 Xt在[0，τk+2]上有定义。在连续极值点[τk，τk+2]区间上定义 Xt的基线提取因子L，即:

式中:a是分解时的增益控制参数，0＜a＜1;Lt保留了信号在各个极值点的单调性，Ht提取了各个极值点之间叠加的局部高频分量信号——固有旋转分量。重复分解过程就可得到一系列固有旋转分量和单调趋势信号。

给出如式(4)所示的仿真信号，它由一个调幅调频信号和一个余弦信号组成:

图1是该仿真信号的波形，图2是运用ITD算法对信号进行分解得到的结果。

图1 仿真信号x(t)Fig.1 Simulation signal x(t)

图2 仿真信号x(t)的ITD分解结果Fig.2 Decomposition result of simulation signal x(t)by ITD

从图2可以看出，分解得到的第1个分量效果较好，但是第2个分量出现了失真，这是因为ITD方法采用线性变换的方法获得基线信号，使得波形出现了毛刺而失真。因此，为了克服该缺陷，本文提出了改进的ITD方法，即采用三次样条插值代替了ITD方法中的线性变换。虽然采用了三次样条插值，但它又不同于EMD中基于局部极值的包络均值，因为ITD改进方法每次分解只需要进行一次三次样条插值。

1.2 ITD 改进方法

文献[8]中虽然给出了ITD方法的详细分解过程，但是并没有对该方法及分解得到的结果的物理意义进行阐述;同时经过以上的研究发现，由于ITD方法采用线性变换的方法实现对信号的分解，从第二个分量开始，出现了较明显的信号失真。因此，本节首先阐述了ITD分解方法的物理意义，接着提出了ITD改进算法。

EMD与LMD方法在提供有效的自适应时频分析方法的同时，提供了一条很好的自适应时频分析思路，即首先假设任意一个复杂信号由若干个瞬时频率具有物理意义的单分量信号组成，并给出瞬时频率具有物理意义的单分量信号所需要满足的条件，然后据此条件对原始信号进行自适应地分解。

在ITD方法中，对于理想的固有旋转分量，其如式(2)所示的基线信号在所有的区间[τk，τk+2]上都应该等于零，因此如式(3)所示的Lk+1应该等于零。理论上ITD方法对信号进行分解得到的固有旋转分量应该满足其基线信号控制点Lk+1等于零。本文在此基础上定义了瞬时频率具有物理意义的内禀尺度分量(Intrinsic Scale Component，ISC)。所定义的ISC分量满足以下条件:

(1)在整个数据段内，任意两个极值点之间呈单调性;

图3 ISC需要满足的条件Fig.3 The needed condition of ISC

(2) 在整个数据段内，其极值点为 Xk，k=1，2，…，M，各个极值点相对应的时刻为 τk，k=1，2，…，M，由任意两个极大(小)值点(τk，Xk)、(τk+2，Xk+2)连接形成的线段在其中间极小(大)值点(τk+1，Xk+1)相对应时刻 τk+1的函数值Xk)与该极小(大)值 Xk+1的比值关系不变，即，即满足，如图3 所示。其中，a∈(0，1)为一常量，典型地，a=1/2，例如正弦或余弦信号、调幅信号、调频信号、调幅－调频信号等。

以上两个条件保证了ISC分量任意两个相邻极值点之间具有单一的模态，而且在局部(极值点与相邻的零交叉点之间)近似吻合标准正弦曲线，因此瞬时频率具有物理意义。

改进的ITD算法假设任何复杂信号是由不同ISC分量组成，任何两个ISC分量之间相互独立，这样就可以将复杂信号分解为若干个ISC分量之和，具体步骤如下:

(1)确定 X(t)的所有极值点 Xk，k=1，2，…，M 及其相对应的时刻 τk，k=1，2，…，M，并设置参数 a，计算各基线控制点Lk，即式(3);然后对所有Lk进行三次样条插值，得到基信号线L1。

(2)将L1从原始信号中分离出来，得到P1。理想地，P1为一个ISC分量，则P1为信号x(t)的第1个分量。理想的ISC分量应满足Lk+1等于零，实际中可以设定变动量Δ，当时迭代结束。

(3)如P1不满足ISC的条件，则将P1作为原始信号重复步骤(1)和(2)，循环k次，直到得到内禀尺度分量Pk，Pk即为信号x(t)的第1个分量ISC1。

(4)将ISC1从x(t)中分离出来，得到一个新的信号r1，将r1作为原始信号重复步骤(1)、(2)和(3)，得到x(t)的第二个满足ISC条件的分量ISC2。重复循环n次，得到信号x(t)的n个满足ISC条件的分量，直到rn为一单调函数为止。这样便可以将x(t)分解为n个内禀尺度分量ISC和一个单调函数rn之和，即:

ISC迭代终止判据Δ的选择对信号的分解和迭代次数都有重要的影响，类似于EMD方法内禀模态函数(IMF)的判据。常用的判据方法有，Huang在文献[9]中介绍的标准偏差法，Flandrin在文献[10]中介绍的三参数法等。其中标准偏差法与IMF分量的定义无关。因此，本文在考虑ISC分量定义的基础上，结合三参数法，来确定变动量Δ的取值。

经过仿真信号分解实验发现，当基线控制点Lk+1与信号的对应极值点Xk+1之比，小于一定取值范围，即Δ取值范围介于0.005时，则得到的分量可以近似为一个ISC分量，此时迭代次数一般为4～10次。

为了减少ITD改进算法中边界效应的影响，在处理数据之前，需对原始数据进行延拓处理，处理方法可采用G.Rilling程序的镜像对称延拓方法[11]。

在处理了端点效应之后，对式(4)所示的仿真信号采用改进ITD算法进行分解，分解时取a=0.5，迭代终止判据，分解后得到如图4所示的两个分量和一个余量，两次的迭代次数分别为5次和4次。采用EMD方法对该仿真信号进行分解，在延拓方法和迭代终止判据相同的情况下，分解结果如图5所示，两次的迭代次数分别为17次和105次。显然，ITD改进算法的迭代次数要少得多，因而分解速率更快。

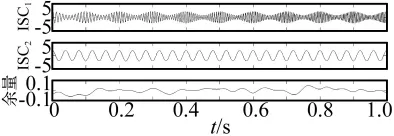
图4 仿真信号的改进ITD分解结果(已处理端点效应)Fig.4 Decomposition result of simulation signal by improved ITD(with boundary processing)

图5 仿真信号的EMD分解结果(已处理端点效应)Fig.5 Decomposition result of simulation signal by EMD(with boundary processing)

图6 是由电涡流位移传感器测得的不平衡故障状态下的转子径向位移振动信号，对其采用ITD改进算法进行分解，共得到3个基本分量和一个余量，如图7所示，从图中可以看出，第1个分量频率成分最高，第2个分量主要为与转速有关的信号，因此故障信息主要包含在第1和第2个ISC分量中，可以选择这两个分量进行组合，得到降噪后的转子信号。

图6 不平衡故障状态下的转子径向位移振动信号Fig.6 Rotor radial displacement vibration signal with unbalance fault

图7 不平衡故障状态下的转子径向位移振动信号的改进ITD分解结果Fig.7 Decomposition result of rotor vibration signal under state of unbalance by improved ITD

2 实验分析

本文采用南京东大测振仪器厂生产的ZT－3型转子振动模拟实验台进行转子系统故障实验，实验装置如图8所示。实验时键相传感器采用电涡流传感器，可以提供相位和转速信号;转子径向位移振动信号由垂直和水平安装的电涡流传感器拾取，信号经过信号调理箱处理后，送入数据采集系统。实验模拟了不平衡、不对中、碰摩和油膜涡动四种故障状态[12]，信号采集时对应转速为3 000 r/min，采样率为4 096 Hz。

图9～12分别是转子在正常、不对中、碰摩、油膜涡动状态下的径向位移振动信号(不平衡状态下的振动信号见图6)。

图8 转子试验台装置Fig.8 Rotor test rig

图9 正常状态下的转子径向位移振动信号时域波形Fig.9 Rotor radial displacement vibration signal under normal state

图10 不对中故障的转子径向位移振动信号时域波形Fig.10 Rotor radial displacement vibration signal with misalignment fault

图11 碰摩故障的转子径向位移振动信号时域波形Fig.11 Rotor radial displacement vibration signal with rub-impact fault

图12 油膜涡动故障的转子径向位移振动信号时域波形Fig.12 Rotor radial displacement vibration signal with oil whirl fault

首先，原始振动信号不进行降噪处理，直接进行分形维数的计算，计算结果如图13所示。考虑到不同嵌入维数下计算得到的关联维数也不同，因此选取了一定范围的嵌入维数，从图中可以看出，各状态对应的分形维数相互交叉，因此对原始信号直接计算关联维数并不能清楚地分辨出转子的工作状态和故障类型。

图13 不同状态转子原始信号在不同嵌入维数下的关联维数Fig.13 The correlation dimension of vibration signals under different embedding dimension

然后，采用ITD改进算法对转子各个状态的原始信号进行降噪处理。即对各信号进行分解，得到若干分量。研究发现，各状态下转子振动信号的故障信息主要集中在前两个分量中，选取了不同状态下转子振动信号的前两个分量重构信号。进一步对这些重构信号计算不同嵌入维数下的关联维数，结果如图14所示。从图中可以看出，经过ITD改进算法降噪后的各状态转子信号在一定嵌入维数范围内的关联维数明确分离，可以明显地区别各工作状态和故障类型，可见转子信号的改进ITD降噪结合关联维数可以准确识别转子的工作状态和故障类型。嵌入维数的选取恰当与否对相空间的重构质量有重要的影响。如果选取过小，将无法容纳系统的吸引子，会出现伪邻近点;反之太大，不仅造成计算工作量大，还减少可使用数据长度，使所建相空间中的相点过于稀疏。关于嵌入维数的选取，实际工程应用中，一般情况，缺少对系统分形维数的先验知识。对于实际系统嵌入维数m的选择比较困难，文献[13]中给出了经验公式m≥D，本文中嵌入维数的范围在5～35时各状态关联维数的区分效果明显。

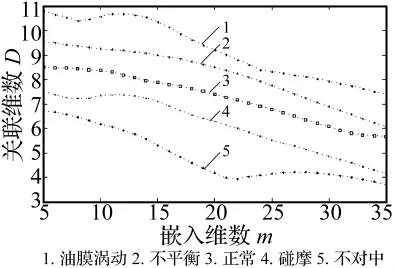
图14 转子信号经改进ITD分解剔除噪声和背景信号后在不同嵌入维数下的关联维数Fig.14 The correlation dimension of vibration signals denoised by improved ITD under different embedding dimension

3 结论

本文将改进ITD算法和关联维数相结合应用于转子的故障诊断中，先通过改进算法对转子信号进行分解降噪，再计算关联维数来提取故障特征，以识别转子的不同工作状态和故障类型。由于关联维数受噪声的影响较大，而转子原始信号中往往含有噪声信号和与转速有关的背景信号，在求取关联维数之前，通过ITD改进算法，可将转子原始信号的故障主要信息提取出来，以剔除噪声和背景信号，再计算关联维数，可获得较好的效果，从而为转子系统故障诊断提供了一种新的方法。值得提出的是，ITD方法刚刚提出，还有许多理论问题需要研究和完善，如迭代终止条件、端点效应等问题，因此对ITD方法的研究还不是很深入。尽管如此，本文所采用的先定义瞬时频率具有物理意义的单分量信号，然后再据此进行自适应信号分解的方法，开拓了时频分析的新思路，对于信号分析和故障诊断都有较大的借鉴意义。

[1]McFadden P D.Window functions for calculating of the time domain averages of the vibration of the individual planet gears and sun gear in an epicyclical gearbox[J].Journal of Vibration and Acoustics，1994，116(1):179 －187.

[2]Alberto R，Maria M.A method for the correlation dimension estimation for on-line condition monitoring of large rotating machinery[J].Mechanical Systems and Signal Processing.2005，19:939 －954

[3]Argyris J.The influence of noise on the correlation dimension of chaotic attractors[J].Chaos Solitions ＆ Fractals，1998，9(3):343－361.

[4]徐美芳，韩 焱，董剑龙.数字射线图像降噪中的线性滤波方法[J].无损检测，2005，27(5):259 －263.XU Mei-fang，HAN Yan，DONG Jian-long.Linear filter methods for image denoising I digital radiography[J].Nondestructive Inspection，2005，27(5):259 －263.

[5]Huang N E，Shen Z，Long S R.A new view of nonlinear water waves:the Hilbert spectrum[J].Annu.Rev.Fluid Mech，1999，31:417－457.

[6]Smith J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface，2005，2(5):443－454.

[7]Lei Y G，He Z J，Zi Y Y.Application of the EEMD method to rotor fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing，2009，23:1327－1338.

[8]Frei M G，Osorio I.Intrinsic time-scale decomposition:timefreqeucny-energy analysis and real-time filtering of nonstationary signals[J].Proceedings of the Royal Society，A，2007，463:321－342.

[9]Huang N E，Shen Z，Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear nonstationary time Series Analysis[J]. Proc. Roy. Soc.London，1998，454:903 －995.

[10]Rilling G，Flandrin P.On empirical mode decomposition and its algorithms[J].IEEE Sig.Pro.Lett，2003:326 －329.

[11]Rilling G，Flandrin P，Goncalves P.On empirical mode decomposition and its algorithms[J].In IEEE-EURASIP Workshop on Nonlinear Signaland Image Processing，Grado，Italy，June 8－11，2003.

[12]赵利华.旋转机械故障机理与轴心轨迹识别方法研究[D].大连:大连理工大学，2010.

[13]Maestrello L.Chaotic response of panel vibrations forced by turbulent boundary layer and sound[J].AIAA Journal，1999，37(3):289 －294.