等截面铁摩辛柯梁－抗转阻尼器系统的复模态特性

陈 勇，刘 盼

(浙江大学 建筑工程学院，杭州 310058)

在加强层和外框架柱之间放置阻尼器是一种新颖的高层建筑振动控制方法[1－2]，这种结构体系可以看成为悬臂梁－抗转阻尼器系统[1]。最近的研究将该悬臂梁近似为欧拉－伯努利梁，阻尼器也只考虑单个[1]。然而实际结构的模态往往还表现出剪切型特征，采用铁摩辛柯梁可以更准确表达这种特征。因此，本文将研究对象明确为一个等截面铁摩辛柯梁连接多个抗转阻尼器的结构体系。

关于该类型结构体系的研究尚未见文献报道。文献中所见的含有抗转阻尼器的系统中的梁通常为欧拉－伯努利梁。例如，Impollonia等[3]研究了附加弯曲刚度的索(带张力的梁)并在端部连有粘滞抗转阻尼器和弹簧时的动力特性。Krenk[4]给出了连接抗转阻尼器的梁结构的复模态分析。通过求解传递函数的根轨迹，Engelen等[5]推导了阻尼系统的复数特征值，并给出了求解系统最大阻尼比和最优阻尼系数的近似方程。Oliveto等[6]给出了两端连有抗转阻尼器的简支梁的自由振动的精确解。

铁摩辛柯梁－阻尼器系统的运动方程具有较为复杂的表达形式，方程中还包含狄拉克函数的一阶导数，因此直接在复数域求解相对困难。Wu等[7]提出的NAM(Numerical Assembly Method)思想可以得到一个线性系统耦合连接离散子系统的自由振动解析解，其应用前提是该线性系统的解析解已知。等截面铁摩辛柯梁的自由振动解已有了大量研究成果[8－11]，表明基于NAM的思想来求解一个等截面铁摩辛柯梁连接多个离散子系统后所形成的耦合系统是可行的。实际上，部分文献对具有实数频率的等截面铁摩辛柯梁连接线性弹簧、抗转弹簧、质量块的问题进行了研究，并获得了相应的解析解[12－13]。

本文首先建立了带有任意数量抗转阻尼器的等截面铁摩辛柯梁的自由振动控制方程，并进行了无量纲化。然后基于NAM思想推导了该铁摩辛柯梁－抗转阻尼器系统的无量纲精确解及特征方程，此特征方程适用于不同边界情况。通过构造实数函数，进行了复特征方程根的复数域数值求解，获得了波数、系统阻尼比及模态，并与有限元结果进行了比较验证。通过数值分析进行了连接单个抗转阻尼器系统的阻尼器最优安装位置、最大阻尼比及相应的最优阻尼系数的研究。并将连接阻尼器后的铁摩辛柯梁与欧拉－伯努利梁结果进行了比较。

1 运动方程及解析解

带有N个抗转阻尼器的等截面铁摩辛柯梁系统如图1所示，图中○中数字表示抗转阻尼器的编号，Cdn(n=1，…，N)表示第n个抗转阻尼器的阻尼系数。坐标系如图所示，坐标原点在左端。该系统的振动控制方程为:

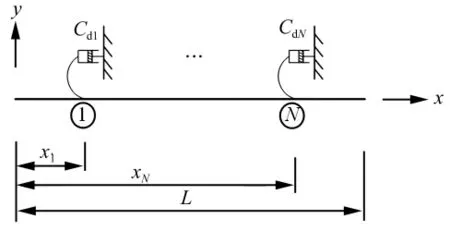
图1 等截面铁摩辛柯梁－抗转阻尼器系统Fig.1 A system of a uniform Timoshenko beam with rotational dampers

其中:y(x，t)为梁的横向位移，φ(x，t)为由弯曲变形引起的截面转角，κ'为截面的剪切系数，G为剪切模量，A为截面面积，E为杨氏模量，I为截面惯性矩，ρ为梁的质量密度，L为梁的跨度，t为时间。

式(1)、(2)可解耦获得:

式(3)、(4)的解可分别写为:

其中引入无量纲参数

将式(5)、(6)、(7)代入式(3)及(4)，可得:

其中:

方程(8)、(9)的解分别为

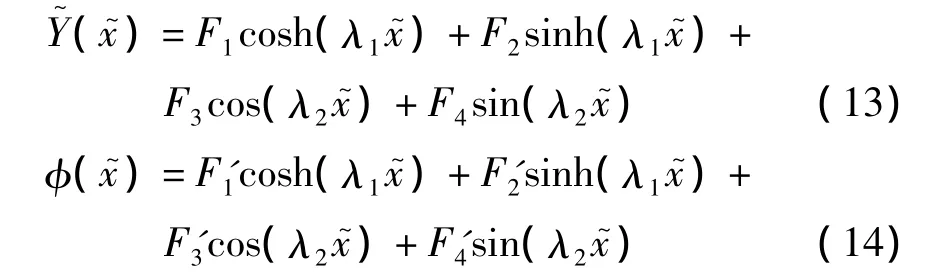
其中:Fj(j=1，…，4)与 F'j(j=1，…，4)为待定系数，波数 λ1，2为:

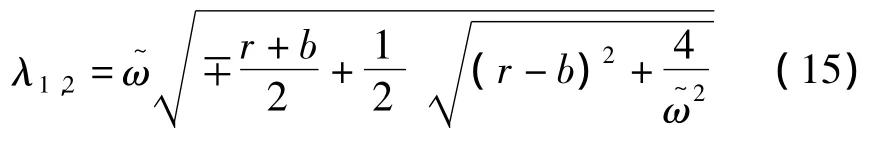
将式(13)、(14)代入式(1)中可得到各系数关系如下:

其中:

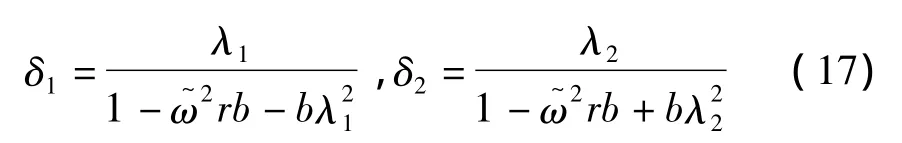
式(13)、(14)分别代表了梁横向位移和由弯曲变形引起的截面转角的幅值函数。通过将梁在阻尼器位置断开，整个梁可以分成(N+1)个节段，每个节段自由振动幅值函数都可以由式(13)、(14)表示。节段连接部位左右截面的不平衡弯矩与抗转阻尼器提供的弯矩之和为零。因此整个系统的边界条件由两端位移边界条件、各连接点处的位移连续条件和力平衡条件组成。写成矩阵形式，可以得到:

对于N个抗转阻尼器系统，系数向量F可以表示为如下形式:

其中:Fn={Fn1，Fn2，Fn3，Fn4}，n表示该系数属于第n个节段。Fnj(j=1，…，4)为第n个节段的4个待定系数。整体系数矩阵D可以表示为:

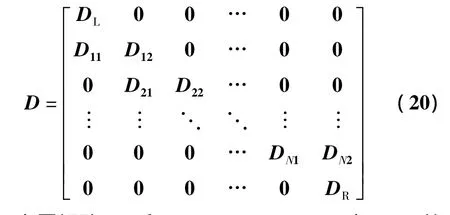
其中:0为零矩阵;Dn1和 Dn2(n=1，2，…，N)为4 ×4 的方阵，可通过第n个连接点处的位移连续条件和力平衡条件得到;DL和DR为2×4的矩阵，可分别通过梁左右两端的位移边界条件得到。

1.1 Dn1及Dn2的表达式

根据式(13)、(14)，第n个节段的横向位移和由弯曲变形引起的截面转角可表示为:

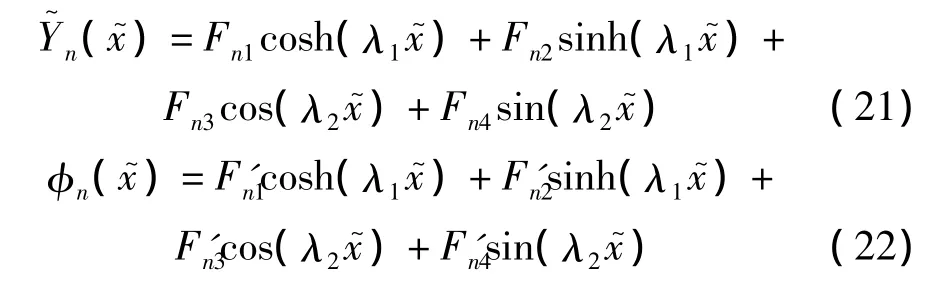
由第n个连接点处的位移连续条件可以得到:

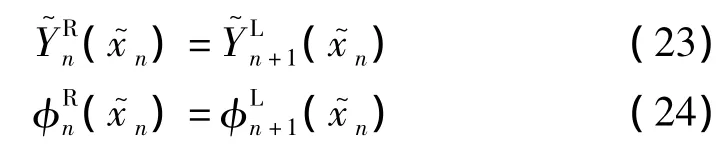
由第n个连接点处的力平衡条件，即弯矩平衡和剪力平衡条件可以得到:

其中:上标‘R’表示梁节段的右端截面，上标‘L’表示梁节段的左端截面。

将式(21)、(22)代入式(23)～(26)得:

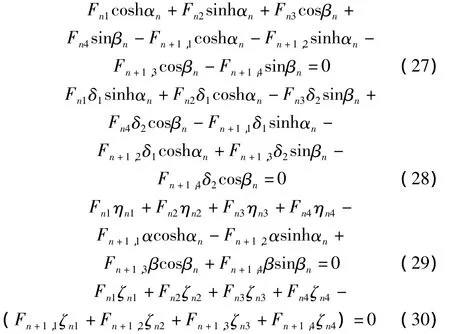
式(27)～(30)式写为矩阵形式:

其中:

且:

1.2 DL及 DR的表达式

图2给出了几种具有不同端部约束条件下的梁示意图。各个梁的DL和DR可根据相应边界条件得到。以左端为自由端的悬臂梁为例，给出DL和DR的形式。

悬臂梁左端自由端的边界条件为:

将式(13)、(14)分别代入式(38)、(39)可得:

式(40)、(41)可写为如下矩阵形式:

其中:

悬臂梁右端固支边界的边界条件为:

将式(13)、(14)分别代入式(44)、(45)可得:

式(46)、(47)可写为:

其中:

对于图2中的其他边界情况，相应的子矩阵DL和DR由下面的式(50)、(51)和(52)给出。

对于图2(b)中的简支梁，

对于图2(c)中的一端铰支一端固支梁，

对于图2(d)中的两端固支梁，

图2 几种等截面铁摩辛柯梁－抗转阻尼器系统Fig.2 Uniform-Timoshenko-beam-rotational-damper systems

2 求解特征方程复数解

式(18)的非平凡解要求系数矩阵D行列式为零，即:

式(53)就是系统复频率的特征方程。令:

则对给定的误差ε和初始~ω值，目标函数χ的最小值即为使式(54)最接近于零的值。

考虑到式(53)具有无穷多个解，因此在求解中需设定合适的初始值。可采用没有阻尼器连接时的梁的频率值作为初始值。

由上述方法求得的自振频率具有复共轭对的形式。本文主要考虑自振频率具有如下形式，即:

其中:ξ为系统阻尼比，ω0为伪无阻尼自振频率。它们可表示为:

通过将已求得的~ω代入到式(18)中，利用高斯消去法可以求得各个待定系数Fnj与F11的关系，则可根据式(13)获得模态振型。

3 数值计算分析

本节所有计算实例所选取的梁均采用以下参数:长度 L=1 m，密度 ρ=7 836.7 kg/m3，弹性模量 E=2×1011N/m2，剪切系数 κ'=5/6，泊松比 υ =0.3，剪切模量，截面宽度 b=0.05 m，截面高度 h=0.15 m。

3.1 连接多个阻尼器的系统

考虑左端铰支右端固支的梁，坐标原点设在铰支端。该梁连接两个抗转阻尼器，其位置分别为=0.3和=0.6。保持0.3位置的阻尼器阻尼系数C1=0.5不变，变化另一个阻尼器的阻尼系数，变化范围为 C2=0 ～1.5，变化增量为 0.001，可得到如图3(a)所示的系统频率的根轨迹图。根轨迹图中的箭头表示参数变化的方向。图3(b)为结构前五阶模态的实数部分，图3(c)为结构前五阶模态的虚数部分，其中||=max|()|。由图 3 可以看出，本文解析解所得结果和有限元法(FEM)结果非常接近，验证了该解析解的正确性。另外，从图中可以看出该系统表现出较强的复模态振动特性，即相位差的存在致使梁上各点振动不会同时达到最大值。这是由于抗转阻尼器所提供的系统阻尼不属于比例阻尼。

3.2 系统阻尼比和相应的阻尼系数

图3 一端简支一端固支的铁摩辛柯梁带有两个抗转阻尼器时的前5阶根轨迹图和模态Fig.3 First five root loci and mode shapes of a hinged-clamped Timoshenko beam with two rotational dampers

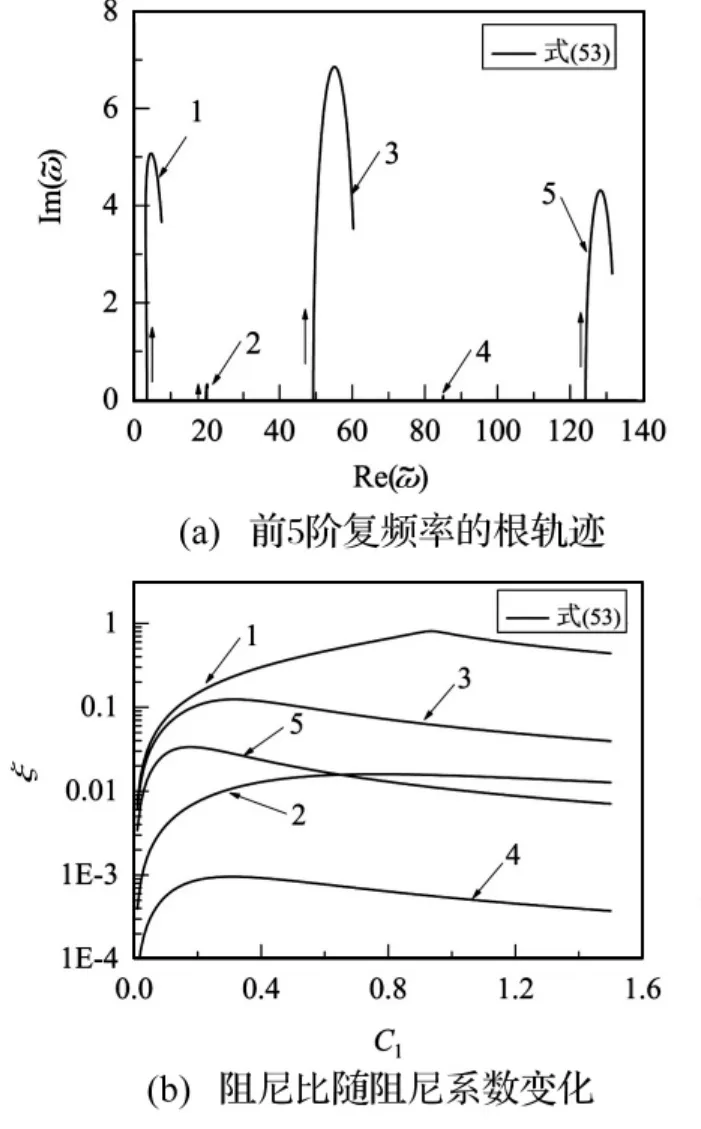
图4 带有单个阻尼器的悬臂梁前5阶根轨迹图及阻尼比Fig.4 First five root loci and damping ratios of a cantilever beam with single rotational damper

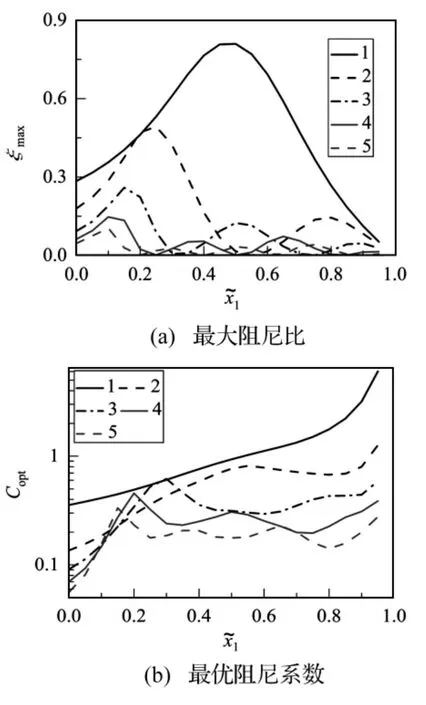
图5 前5阶模态的最大阻尼比及相应最优阻尼系数随阻尼器位置的变化Fig.5 Maximum damping ratios and corresponding optimum damping coefficients varying with damper’s position

图6 两种梁的系统振动特性对比Fig.6 Comparison of Timoshenko beam system and Euler-Bernoulli beam system

考虑带有单个阻尼器的右端固支悬臂梁，坐标原点设在自由端。对于阻尼器位置 ~x1=0.5时的情形，图4(a)给出了相应的根轨迹图，可以发现系统的频率随着阻尼系数的增加而增加，阻尼比并没有一直随着阻尼系数的增加而增加。相应地，图4(b)给出了由式(57)得到的阻尼比随阻尼系数的变化情况。可见:当阻尼器位置 ~x1确定时，存在一个最大阻尼比ξmax;对不同的模态，最大阻尼比ξmax所对应的阻尼系数Copt(最优阻尼系数)并不相同。

图5(a)给出了最大阻尼比ξmax随阻尼器位置~x1的变化关系。每一阶模态都可以找到一个最优阻尼器位置，使得最大阻尼比ξmax取最大值，记作系统最大阻尼比ξtmax。一阶模态的系统最大阻尼比 ξtmax达到了0.809 72，并随着模态阶次的增加而减少，第5阶模态的ξtmax为0.104 38。铁摩辛柯梁安装单个抗转阻尼器时的对应于第m(m=1，…，5)阶模态的最优安装位置为梁的2m等分点，且靠近自由端的等分点位置对应的模态阻尼比较大。这与文献[1]中欧拉梁的结果相近，即最优安装位置近似服从以下规律:

3.3 等截面铁摩辛柯梁和欧拉－伯努利梁结果比较

考虑带有单个阻尼器的右端固支悬臂梁振动系统，阻尼器位置为 ~x1=0.5，分别采用铁摩辛柯梁及欧拉－伯努利梁进行分析。图6给出两种梁的对应于前五阶模态的自振频率及阻尼比随阻尼系数的变化。从图中可看出，抗转阻尼器对欧拉－伯努利梁系统的自振频率提高相对较大。欧拉－伯努利梁系统的对应于奇数阶模态的阻尼比相对于铁摩辛柯梁更高，偶数阶则相反。

4 结论

针对带有抗转阻尼器的等截面铁摩辛柯梁的自由振动问题，本文推导了系统的精确解及特征方程，并给出了在复数域求解特征方程的方法。参数分析表明:

(1)该非比例阻尼系统存在系统最大阻尼比和最优阻尼系数。该系统表现出较强的复模态振动特性，即相位差的存在致使梁上各点振动不会同时达到最大值。

(2)悬臂铁摩辛柯梁连接单个阻尼器时:系统的频率随着阻尼系数的增加而增加;第m阶模态的最优阻尼器安装位置为梁的各个2m等分点，且靠近自由端的等分点位置对应的模态阻尼比较大;与采用欧拉－伯努利梁分析得到的结果相近。一阶模态的系统最大阻尼比ξtmax达到了0.809 72，并随着模态阶次的增加而减少。

(3)将连接抗转阻尼器的铁摩辛柯梁和欧拉－伯努利梁比较表明，最优阻尼器安装位置较为接近。将阻尼器安装在跨中时，抗转阻尼器对欧拉－伯努利梁系统的自振频率提高相对较大，获得的第一阶模态阻尼比也相对于铁摩辛柯梁更高。

[1]Chen Y，McFarland D M，Wang Z，et al.Analysis of tall buildings with damped outriggers[J].Journal of Structural Engineering，2010，136(11):1435－1443.

[2]Smith R J，Willford M R.The damped outrigger concept for tall buildings[J].The Structural Design of Tall and Special Buildings，2007，16:501 －517.

[3]Impollonia N，Ricciardi G，Saitta F.Dynamic behavior of stay cables with rotational dampers[J].Journal of Engineering Mechanics，2010，136(6):697 －709.

[4]Krenk S. Complexmodesand frequenciesin damped structural vibrations[J].Journal of Sound and Vibration，2004，270:981－996.

[5]Engelen K，Ramon H，Saeys W，et al.Positioning and tuning of viscous damper on flexible structure[J].Journal of Sound and Vibration，2007，304:845－862.

[6]Oliveto G，Santini A，Tripodi E.Complex modal analysis of a flexural vibrating beam with viscous end conditions[J].Journal of Sound and Vibration，1997，200(3):327－345.

[7]Wu J S，Lin T L.Free vibration analysis of a uniform cantilever beam with point masses by an analytical-andnumerical-combined method [J].Journal of Sound and Vibration，1990，136(2):201－213.

[8]陈 镕，万春风，薛松涛，等.Timoshenko梁运动方程的修正及其影响[J].同济大学学报(自然科学版)，2005，33(6):711－715.

[9]楼梦麟，任志刚.Timoshenko简支梁的振动模态特性精确解[J].同济大学学报，2002，30(8):911－915.

[10]蒋纯志，李海阳.基于传递函数解的铁木辛柯梁分析[J].湖南理工学院学报(自然科学版)，2006，19(2):19－21.

[11]蒋纯志，金 桂，陈亚琦.等截面铁木辛柯梁的分布传递函数方法[J].湖南科技学院学报2009，30(8):50－53.

[12]Lin H Y.On the natural frequencies and mode shapes of a multispan Timoshenko beam carrying a number of various concentrated elements[J].Journal of Sound and Vibration，2009，319:593－605.

[13]Wu J S，Chen D W.Free vibration analysis of a Timoshenko beam carrying multiple spring-mass systems by using the numerical assembly technique[J].International Journal for Numerical Methods in Engineering，2001，50:1039 －1058.