泡沫铝夹芯圆筒抗爆性能研究

刘新让，田晓耕，卢天健，梁 斌，王伊卿

(1.西安交通大学 机械结构强度与振动国家重点实验室，西安 710049;2.中国矿业大学 徐海学院，徐州 221008;3.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

无论是在军事领域还是民用领域，爆炸冲击防护都极为重要。合理设计的、由单一材料制成的实体防爆结构虽然能够满足防爆要求，但通常会使得被保护装置异常笨重，限制了其灵活性，尤其是在有移动需求的防护场合，如警用防爆罐、舰船、特种汽车等。近年来，国内外的反恐斗争对防爆罐的便携性提出了更高要求，开发新型轻质抗爆结构的重要性和迫切性日益突出。

由于闭孔泡沫铝夹芯结构具有密度低、吸能高等优良的力学性能，对有效提高防爆结构的抗爆性具有显著的应用价值，吸引了国内外众多学者对其抗爆性能进行研究。Sriram等[1]对面板材料为环氧玻璃、芯层材料为泡沫铝的三明治夹芯结构在爆炸作用下的响应进行了数值模拟，分别讨论了面板、泡沫铝芯层和三明治夹芯板这3种结构在爆炸载荷作用下的响应，并模拟了一个由这种夹芯板组成的立方盒子在承受内部爆炸作用下的响应，发现立方盒中夹芯板的连接部位的应力较高，说明利用夹芯板制造抗爆装备时，需要对板的连接处进行加固。Zhu等[2]采用实验和数值模拟方法，研究了四周固支泡沫铝夹芯板在爆炸载荷作用下的动力响应和能量吸收问题，比较了不同参数泡沫铝夹芯板后面板中心处的最大位移，实验发现夹芯板在爆炸载荷作用下发生塑性变形，由于泡沫铝芯层的断裂失效，在前面板和芯层之间会产生空洞;数值模拟结果与实验结果较为吻合;最后，通过实验比较了不同参数夹芯板的能量吸收性能，阐明了夹芯板不同参数和不同炸药装药量对其能量吸收能力的影响。他们还研究了方形蜂窝铝夹芯板在爆炸载荷作用下的动力响应[3]，模拟结果和实验测量的结果符合得较好，发现四周固支条件下面板的拉伸性能对夹芯板中心的位移起决定作用。Theobald等[4]对面板材料是钢、芯层材料是Alporas泡沫铝或六边形蜂窝的夹芯板进行了空中爆炸实验研究，对于每种芯层材料、面板都采用了两种不同厚度。实验结果表明，厚面板夹芯板的抗爆性能好，且厚面板蜂窝夹芯板的抗爆性能最好。Shen等[5]实验研究了面板材料为铝、芯层材料为泡沫铝的曲率夹芯板在空中爆炸载荷作用下的响应，发现曲率夹芯板比等重量的实体板和夹芯平板更具优势。

近年来，国内学者也开展了相关的研究。石少卿等[6]采用理论分析和数值模拟方法，研究了泡沫铝夹芯板对爆炸冲击波的削弱作用，表明钢板－泡沫铝－钢板复合结构具有较好的吸能减振效果，可以运用到地面军事结构防爆设计中，提高地面军事建筑的战时生存能力。任新见等7]对泡沫金属夹芯板的抗爆机理进行了初步探讨，发现泡沫金属夹芯结构具有显著的消波吸能性能，在防护工程抗爆中具有广泛的应用前景和实用价值。田杰等[8]采用实验和数值模拟的方法研究了泡沫铝作为底板材料对爆炸冲击波在结构后产生的次生冲击波超压的衰减情况，发现采用泡沫铝作为底板材料，不仅能降低底板的质点速度，减小结构后次生冲击波的峰值，同时还能减少结构的重量。最后通过数值模拟研究了泡沫铝的不同排列方式对其防爆效果的影响，发现波阻抗按照从小到大的顺序排列结构的整体变形最小，结构后面空气中的次生冲击波也最小。韩守红等[9]数值分析了6种泡沫铝夹芯板的抗爆性能，从中选出了最优结构，并分析了泡沫铝芯层对夹芯板动力响应的影响，同时应用自适应响应面法对夹芯板的上、下面板厚度和芯层厚度进行了优化设计，夹芯板的抗爆性能得到明显改善。王灿等[10]考虑泡沫铝的应变率效应、用三维物质点方法分析了泡沫铝夹芯结构在爆炸冲击载荷作用下的抗爆性能，计算了夹芯结构各层在冲击中和冲击后的塑性变形和载荷分布，结果表明，泡沫铝夹芯结构具有优越的抗爆性能。

由以上可知，夹芯结构在爆炸载荷作用下的动力响应问题得到了研究者的广泛关注，但是到目前为止研究工作还相当有限，且研究大都局限于简单的梁板结构，离实际工程应用还有较大距离。本文将研究对象扩展到夹芯圆柱壳结构，并把结构应用于新型防爆罐的设计中，基于流固耦合方法，运用LS-DYNA软件分析其在爆炸载荷作用下的响应。国内学者已经对爆炸模拟进行了比较广泛的研究，赵桂范和王伟东[11]讨论了爆炸冲击有限元分析中的一些关键问题，在模拟爆炸方面，比较了JWL方程和高压气体这两种模拟方法;在耦合方面，比较了一般耦合和ALE耦合。吴桂英等[12]采用ALE方法模拟了球壳在爆炸载荷作用下的动力反直观行为，对球壳的矢高和厚度对其反直观行为的影响进行了参数分析，得到了球壳中位移时程曲线和最终变形模式等动力响应。王定贤等[13]运用ANSYS/LS-DYNA对爆炸容器爆心截面的环向应变进行了数值模拟，同时做了实验对比研究，比较模拟结果与实验结果发现，两种方法所得峰值应变相近，且峰值到达时间基本一致，但因实际容器的结构响应有多种振型参与，使得实验波形比模拟波形复杂。高轩能等[14－15]应用 ANSYS/LS-DYNA 建立了大空间柱壳结构在爆炸载荷作用下的冲击波压力场计算模型，首先验证了模型及参数选取的可靠性，接着引入本征正交分解法解决了冲击波荷载的时空差异性和结构表面压力场分布问题。研究结果表明，计算模型适用于大空间结构的爆炸动力响应分析，并对跨度和矢跨比等因素对结构动力响应的影响进行了数值分析。

本文采用LS-DYNA软件模拟了夹芯圆柱壳结构在爆炸载荷作用下的动力响应，同时模拟了相同重量的实体圆筒作为对比，为新型轻质防爆装置的设计提供科学依据。

1 模拟方法有效性验证

为了验证本文所用模拟方法的有效性，首先对文献[2]给出的泡沫铝夹芯板的实验结果进行了数值模拟。夹芯板的上、下面板均为Al－2024－T3铝合金，芯层是相对密度为6%的闭孔泡沫铝。夹芯板长宽均为250 mm，四周固支，面板和芯层采用不同厚度进行配置，如表1所示。炸药距离上面板(离炸药较近的面板)中心的距离为200 mm，如图1(a)所示，炸药为圆柱形的TNT，在其顶面中心起爆，不同夹芯板对应的炸药量如表1所示。夹芯板的抗爆性能由下面板的法向位移度量，实验测量结果列于表1中[2]。

模拟采用流固耦合方法，建模时需要建立空气模型作为耦合域将夹芯板完全包裹起来，单位制为爆炸单位制，即长度、重量和时间的单位分别为厘米、克和微秒。流固耦合的相关参数设置列于表2中，其中NQUAD代表耦合积分点数，取值为0表示每个Lagrange单元表面有2×2个耦合点;CTYPE代表耦合类型，取值为5表示耦合为允许Lagrange实体出现侵蚀的罚函数耦合;DIREC代表耦合方向，取值为3表示在所有方向都要耦合;MCOUP代表多物质选项，取值为0表示与所有的多物质组进行耦合;PFAC代表罚函数系数，取值0.15用于计算耦合力。

式(1)中:C0、C1、C2、C3、C4、C5和 C6为常数，在本模拟中 C0= －0.1 MPa，C1=C2=C3=C6=0，C4=C5=0.4，初始内能密度 E0=2.5 ×105J/m3，初始相对体积V0=1。

炸药类型为TNT，其密度为1 630 kg/m3，爆速为6 700 m/s，爆压为 19 GPa，采用 MAT_HIGH_EXPLOSIVE_BURN本构模型，与该本构模型匹配的状态方程采用EOS_JWL，状态方程中压力P同样定义为相对体积V和内能密度E的函数，如式(3)所示:

表1 泡沫铝夹芯板的配置和实验结果Tab.1 Specifications of aluminum foam-cored sandwich panels and experimental results[2]

表2 流固耦合的相关参数Tab.2 Related parameters of fluid-structure interaction

由于夹芯板和爆炸载荷的对称性，只建立1/4计算模型，并施加对称约束和固支约束，如图1(b)所示。对于空气模型，在对称面上施加对称约束，其余面则定义为无反射边界来模拟在无限空间的爆炸。网格剖分时夹芯板为Lagrange网格，空气模型为Euler网格，两种网格通过ALE方法耦合起来。整个模型的单元类型均为采用减缩积分的八节点实体单元SOLID164，为了保证数值计算的收敛性，其中Lagrange单元剖分为10 800个，Euler单元剖分为94 192个，如图1(a)所示。

图1 1/4计算模型Fig.1 A quarter of sandwich panel and air domain

空气的密度为1.29 kg/m3，采用MAT_NULL本构模型，与该本构模型匹配的状态方程采用EOS_LINEAR_POLYNOMIAL，状态方程中压力P定义为相对体积V和内能密度E的函数，如式(1)和式(2)所示:

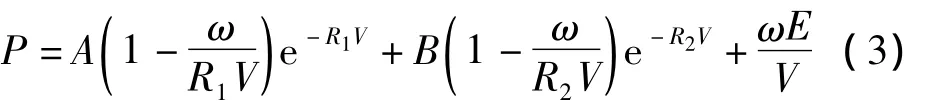
其中:A、B、R1、R2和ω为输入参数，本模拟中炸药状态方程的相关参数如表3所示。

表3 TNT炸药状态方程的相关参数Tab.3 Related parameters of EOS for TNT explosive

面板材料为 Al－2024 － T3[2]，采用 MAT_PLASTIC_KINEMATIC本构模型，强化方式为随动强化，因其应变率效应不明显，模拟中未考虑，其中密度ρ=2 680 kg/m3，弹性模量 E=72 GPa，泊松比 υ =0.33，屈服应力σY=318 MPa，切线模量Et=737 MPa。

芯层材料为闭孔泡沫铝，采用MAT_HONEYCOMB本构模型，其中密度ρ=160 kg/m3，压缩应力－应变曲线采用文献[2]中的数据。

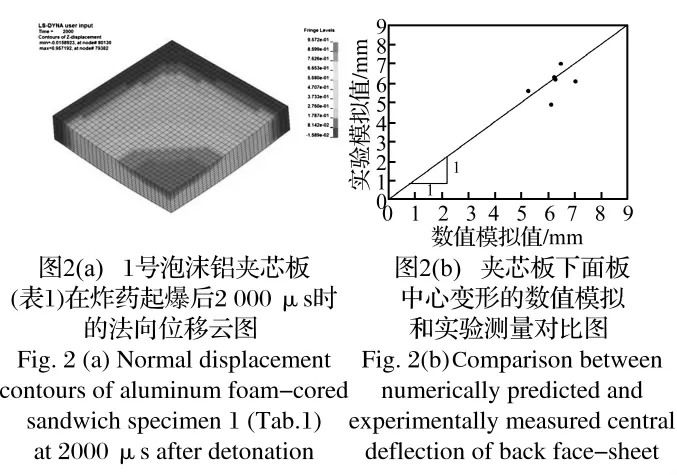
图2(a)给出了试件1的法向位移云图，图中量值的单位为cm，由于炸药距离夹芯板中心最近，夹芯板中心处的位移最大，与实际情况相符。图2(b)为夹芯板下面板中心最大变形的模拟结果和实验结果的对比图，以模拟结果为横坐标，实验结果为纵坐标，理想情况是数据点落在45°斜线上。从图2(b)可以看出数据点分布在45°斜线两侧附近，可见模拟结果和实验结果吻合较好，说明本文所采用的模拟方法是有效的。

2 计算模型及材料参数

2.1 计算模型

闭孔泡沫铝夹芯圆筒如图3所示，筒壁高2H=800 mm，底板厚度Hb=20 mm，内直径d=596 mm，外直径D=796 mm。筒壁为三明治夹芯结构，内、外面板均为A3钢，芯层为闭孔泡沫铝，内面板厚度ti=2 mm，外面板厚度to=8 mm，泡沫铝芯层厚度tc=90 mm。底板材料与内、外面板相同，芯层材料为东南大学制备的闭孔泡沫铝，相对密度为10%，密度为270 kg/m3。这里着重考察筒壁在爆炸载荷作用下的动力响应，所以筒壁顶部没有加盖子。作为对比，同时构造了相同重量的A3钢实体圆筒，圆筒内直径d=596 mm保持不变，按照重量等效原则，计算筒壁厚度为18.1 mm。模拟中炸药为球形TNT，如图4(b)所示，起爆方式为中心单点起爆，炸药位于圆筒中轴线的一半高度处。

由于圆筒结构和爆炸载荷的对称性，只建立圆筒及空气的1/4模型，如图4(a)所示。在圆筒底部施加固定约束，在对称面上施加对称约束。计算模型由两个部分组成，一是夹芯圆筒，划分为Lagrange网格;二是空气模型，划分为Euler网格。网格剖分后的模型如图4(b)所示，整个模型的单元类型均为SOLID164，为保证数值结果的收敛性，其中划分Lagrange单元43 301个，Euler单元219 024个。对相同重量的实体圆筒采用同样的处理方法，划分Lagrange单元8 759个，Euler单元138 915个。

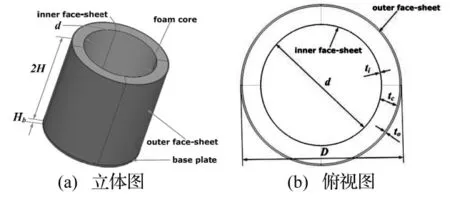
图3 夹芯圆筒结构示意图Fig.3 Skematic of sandwich-walled hollow cylinder

图4 1/4计算模型Fig.4 A quarter of sandwich-walled hollow cylinder and air domain

2.2 材料参数

A3钢采用MAT_PLASTIC_KINEMATIC本构模型，强化方式为随动强化，通过Cowper-Symonds模型考虑材料的应变率效应，屈服应力放大系数的计算公式为:

式中:σd为动态屈服应力，σY为屈服应力为应变率，C和P为材料应变率效应常数。具体材料参数为:密度ρ=7 850 kg/m3，弹性模量E=210 GPa，泊松比υ=0.3，屈服应力 σY=240 MPa，切线模量 Et=2 GPa，材料常数 C=105s－1，P=5。

张健等[16]对东南大学闭孔泡沫铝的应变率效应进行了研究，发现该泡沫铝(相对密度10%)的应变率效应不明显，应用中可以忽略，其准静态压缩应力－应变曲线如图5所示，模拟中泡沫铝芯层采用MAT_HONEYCOMB本构模型。

空气和TNT炸药的本构模型和状态方程与前文第1部分相同。

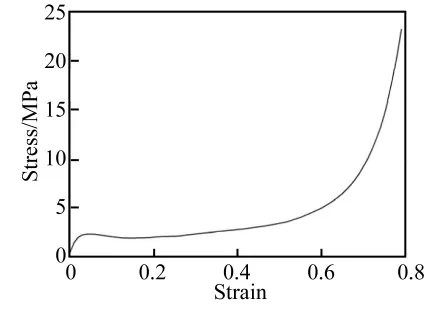
图5 闭孔泡沫铝(相对密度10%)的准静态单轴压缩应力－应变曲线Fig.5 Quasi-static stress-strain curve of close-celled aluminum foam(relative density 10%)obtained from uniaxial compression test

3 模拟结果分析

3.1 夹芯圆筒和实体圆筒的抗爆性能

由于TNT炸药的装药位置为圆筒中轴线的一半高度处，在爆炸载荷作用下，圆筒的中间部位将产生最大的径向变形，如图6所示，图中量值的单位为cm。鉴于此，在靠近泡沫铝芯层的内、外面板上各选择一个节点作为特征节点，其中内面板的节点编号为3 428，外面板的节点编号为11 091，两节点在图6中做了标记，计算时提取这两个特征节点的径向位移作为圆筒变形的度量。由于实体圆筒内外表面的径向变形差别较小，仅在实体圆筒筒壁的中间部位提取一个特征节点描述其径向变形。下面所提到的径向变形，均为圆筒中间部位的最大径向变形。

图7比较了实体圆筒和夹芯圆筒在2 kg炸药爆炸载荷作用下的径向变形。由图可知，夹芯圆筒内面板虽然产生了46.9 mm的径向变形，但由于泡沫铝芯层的塑性坍塌，外面板产生的径向变形却很小，仅为1.7 mm;而相同重量的钢制实体圆筒在相同爆炸载荷下的径向变形为4.5 mm，远大于夹芯圆筒外面板的径向变形，可见通过泡沫铝芯层的压缩变形和塑性坍塌有效降低了圆筒结构的整体变形。

图6 夹芯圆筒在2 kg炸药起爆后1 500 μs时的径向位移云图和特征节点选取Fig.6 Radial displacement contours of sandwich-walled hollow cylinder at 1 500 μs after 2 kg explosive detonation and selection of representative nodes

图7 2 kg炸药下夹芯圆筒与实体圆筒的径向变形Fig.7 Radial deflections of sandwich-walled and monolithic-walled hollow cylinders under 2 kg explosive

炸药爆炸时产生的能量除了以光、热和声响等方式耗散以外，其余则通过空气传递给圆筒结构，转化为圆筒的内能和动能。图8和图9分别对比了夹芯圆筒与实体圆筒在2 kg炸药爆炸载荷作用下的内能和动能。由图8可知泡沫铝芯层吸收的内能最多，而这正符合夹芯圆筒通过泡沫铝芯层来吸能的设计目的，为84 kJ，内面板为 40.8 kJ，外面板为 3.3 kJ;而相同重量实体圆筒的内能变化仅为15.2 kJ，远小于夹芯圆筒所吸收的能量。从图8还可看出，泡沫铝芯层是主要的吸能部分，这源于闭孔泡沫铝具有较长的平台应力段(图5)，因而吸能性能优秀;内面板因为产生了大的塑性变形而吸收大量能量，而外面板塑性变形小，吸能很少。由图9可见，圆筒各部分的动能在爆炸载荷下迅速达到峰值，并在内、外面板塑性弯曲和拉伸以及芯层塑性压缩的作用下快速衰减，其中内面板获得的动能最大，为 34.2 kJ，泡沫铝芯层为 14.4 kJ，而相同重量实体圆筒的动能仅为5.9 kJ，远小于夹芯圆筒转化的动能。从图9还可看出，实体圆筒在动能衰减后会有长时间的微幅震荡，这是由于实体圆筒阻尼较小的缘故;与之相反，夹芯圆筒由于泡沫铝芯层阻尼很大而几乎没有震荡发生。

通过模拟实体圆筒和夹芯圆筒在2 kg炸药爆炸载荷作用下的响应可以看出，无论是在圆筒整体变形方面，还是在能量吸收方面，夹芯圆筒均优于实体圆筒。

由于被保护的人员或设备位于圆筒的外面，因而圆筒的整体变形是衡量抗爆性能的一个重要指标，图10比较了在1 kg、2 kg和3 kg这3种炸药量下夹芯圆筒外面板的径向变形和实体圆筒筒壁的径向变形。由图可知，在3种炸药量下，夹芯圆筒外面板的径向变形均小于相同重量实体圆筒筒壁的径向变形，这说明泡沫铝芯层的塑性压缩减小了夹芯圆筒的整体变形，提高了抗爆性能。其中，在3 kg炸药量下，由实体圆筒的10.9 mm减小为夹芯圆筒的8.8 mm，减小了19.3%;在2 kg炸药量下，由实体圆筒的4.5 mm减小为夹芯圆筒的1.7 mm，减小了62.2%;在1 kg炸药量下，实体圆筒的径向变形为0.7 mm，而夹芯圆筒外面板就没有发生塑性变形。

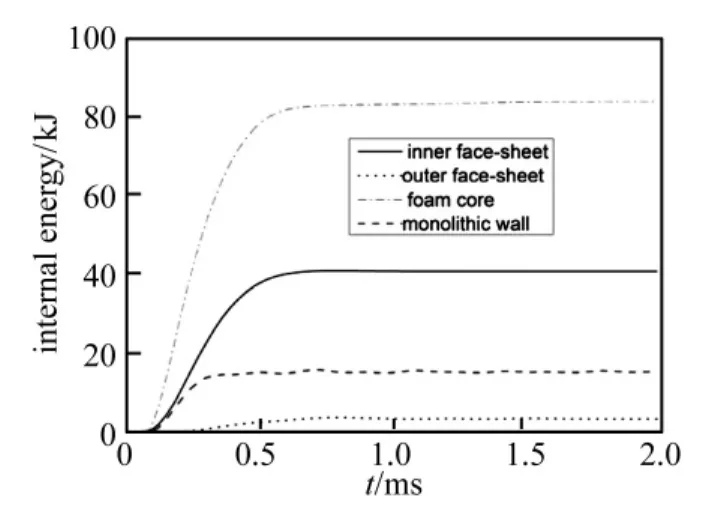
图8 2 kg炸药下夹芯圆筒与实体圆筒的内能Fig.8 Internal energy of sandwich-walled and monolithic-walled hollow cylinders under 2 kg explosive

图9 2 kg炸药下夹芯圆筒与实体圆筒的动能Fig.9 Kinetic energy of sandwich-walled and monolithic-walled hollow cylinders under 2 kg explosive

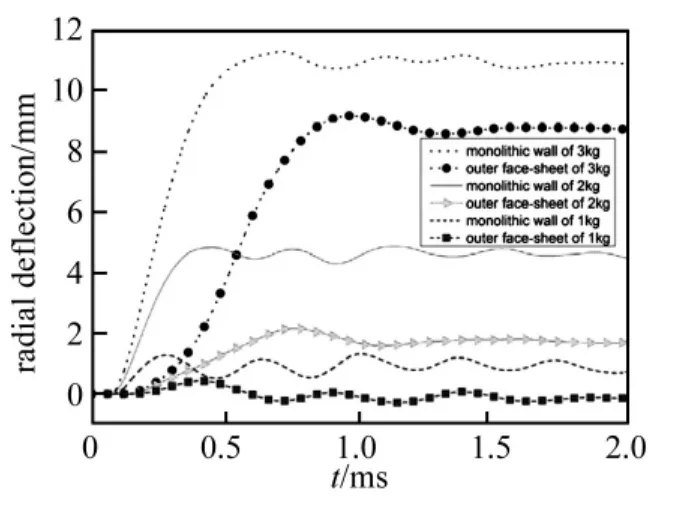
图10 夹芯圆筒与实体圆筒在不同炸药量下的径向变形Fig.10 Radial deflections of sandwich-walled and monolithic-walled hollow cylinders subjected to different blast loading

由上面分析可知，泡沫铝芯层是主要的吸能部分，所以选择夹芯圆筒的芯层内能和实体圆筒内能进行比较，如图11所示。由图可知，在3 kg炸药量下，芯层的内能为165.3 kJ，而实体圆筒的内能为38.7 kJ;在2 kg炸药量下，芯层的内能为84 kJ，而实体圆筒的内能为15.2 kJ;在 1 kg 炸药量下，芯层的内能为 23.2 kJ，而实体圆筒的内能为3.1 kJ。即在3种炸药量下，夹芯圆筒的芯层内能均远远大于相同重量实体圆筒的内能，这说明夹芯圆筒能更有效地吸收爆炸能量，减少爆炸能量对周围环境的影响。图12比较了泡沫铝夹芯圆筒在3种炸药量下的芯层压缩量，而芯层压缩量定义为图6中所示两个特征节点的径向位移之差。由图12可知，芯层压缩量随着炸药量的减小而减小，炸药量从3 kg 到 1 kg，芯层压缩量分别为 60.5 mm、45.2 mm 和20.9 mm。对比图11和图12可知，在3种炸药量下，芯层压缩量的变化与芯层内能的变化保持同步，压缩量越大则芯层吸收的能量就越大，这反映了泡沫铝吸能是通过压缩变形来完成的。

由上面分析可知，因为距离炸药最近，内面板获得的动能最大，所以提取夹芯圆筒的内面板动能和实体圆筒动能进行比较，如图13所示。从图中可以看出，在3 kg炸药量下，夹芯圆筒的动能为69.7 kJ，而实体圆筒的动能为14.9 kJ;在2 kg炸药量下，夹芯圆筒的动能为34.2 kJ，而实体圆筒的动能为5.9 kJ;在1 kg炸药量下，夹芯圆筒的动能为9.5 kJ，而实体圆筒的动能为1.6 kJ。即在3种炸药量下，夹芯圆筒的内面板动能均远远大于相同重量实体圆筒的动能，而这正发挥了内面板的作用，其在爆炸载荷作用下发生剧烈的运动和变形，从而把爆炸载荷传递给泡沫铝芯层。

图14给出了夹芯圆筒在2 kg炸药引爆后390 μs时的应力云图，图中量值的单位为105MPa，由图可知圆筒应力较大的部位有两处，分别是筒壁与底板的连接部位和圆筒的中间部位。爆炸冲击波在筒壁与底板处发生反射产生反射冲击波，反射波的相互作用造成筒壁与底板连接部位的应力较大，故在实际应用中需要对连接部位进行必要的加强。圆筒中间部位因为距离炸药最近，因而应力也较大。在中间部位靠近泡沫铝芯层的内、外面板上各取一个单元作为特征单元，其位置与图6中所取节点的位置相对应，同时在实体圆筒的相应位置选取一个单元，提取这3个单元的Mises应力作对比，在2 kg炸药爆炸载荷作用下的应力时程曲线如图15所示。由图可知，内面板应力峰值远大于外面板应力峰值;经过泡沫铝芯层的衰减作用，峰值应力从内面板的604.4 MPa降到外面板的289.8 MPa，减小了52%，这说明泡沫铝发挥了良好的消波作用，而外面板应力峰值较低导致夹芯圆筒整体变形较小(图7)。实体圆筒的筒壁应力为327.8 MPa，大于夹芯圆筒外面板的应力，这说明夹芯圆筒比实体圆筒具有更好的抵抗破裂的能力，能更有效地避免圆筒结构破裂所造成的二次伤害。

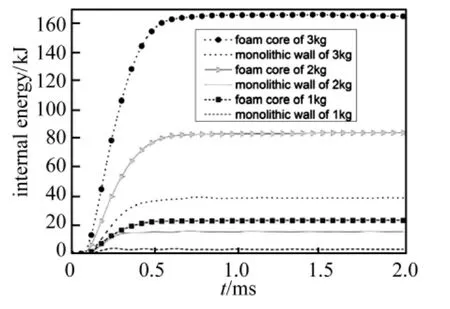
图11 夹芯圆筒与实体圆筒在不同炸药量下的内能Fig.11 Internal energy of sandwich-walled and monolithic-walled hollow cylinders subjected to different blast loading

图12 夹芯圆筒在不同炸药量下的芯层压缩Fig.12 Core crushing of sandwich-walled hollow cylinders subjected to different blast loading

图13 夹芯圆筒与实体圆筒在不同炸药量下的动能Fig.13 Kinetic energy of sandwich-walled and monolithic-walled hollow cylinders subjected to different blast loading

图14 夹芯圆筒在2 kg炸药起爆后390 μs时的应力云图Fig.14 Von mises stress contour plot of sandwich-walled hollow cylinder at 390 μs after 2 kg explosive detonation

图15 2 kg炸药下夹芯圆筒与实体圆筒的Mises应力Fig.15 Von mises stresses of sandwich-walled and monolithic-walled hollow cylinders under 2 kg explosive

图16 2 kg炸药下内面板一半高度处空气单元(79794)的压力时程曲线Fig.16 Pressure time history of air element 79794 at the middle height of inner face-sheet under 2 kg explosive

图6 中内面板节点编号为3 428处相应空气单元的编号为79 794，提取该空气单元的压力时程曲线，如图16所示。由图可知，初始压力峰值为57.9 MPa，相应的峰值时间为0.1 ms，而因为爆炸冲击波遇到内面板反射所产生的压力峰值却很小，仅为4.9 MPa，相对初始压力峰值减小了91.5%。

3.2 不同配置夹芯圆筒的抗爆性能

为了研究不同配置对抗爆性能的影响，这里研究了5种不同配置(保持夹芯圆筒的内、外面板厚度之和等于10 mm不变)夹芯圆筒在2 kg炸药作用下的响应，从配置1到配置5，内面板厚度逐渐增大，而外面板厚度逐渐减小，5种配置方式如表4所示，表中同时列出了每种配置方式的外面板径向变形和夹芯圆筒重量。

表4 夹芯圆筒的5种不同配置方式Tab.4 Five different specifications of sandwich-walled hollow cylinders

图17给出了5种不同配置夹芯圆筒的外面板径向变形，从图中可以看出，配置5的外面板径向变形最大为4.3 mm，配置2的外面板径向变形最小为0.9 mm，配置2相对配置5减小了79%，可以看出夹芯圆筒的不同配置方式对外面板径向变形有显著影响。同时配置1的外面板径向变形1.7 mm小于配置5的4.3 mm，配置2的外面板径向变形0.9 mm小于配置4的2.2 mm，可以看出在减小外面板径向变形方面，采用薄内面板、厚外面板的配置要优于厚内面板、薄外面板的配置，分析可知厚的外面板能起到较好的约束作用，因而降低了外面板径向变形。虽然配置1的外面板厚度8 mm大于配置2的外面板厚度6 mm，但配置1的外面板径向变形1.7 mm却大于配置2的0.9 mm，这是因为配置1相比配置2吸收了更多的爆炸能量，具体吸能见图18(b)。而采用内、外面板厚度相等的配置3也具有相当优势，其外面板径向变形仅为1.4 mm。

图18(a)比较了5种不同配置夹芯圆筒在2 kg炸药下的芯层压缩量，图18(b)比较了芯层内能。对比两图可以看出，和3.1部分的结果类似，芯层压缩量和芯层内能保持同步变化关系，且从配置1到配置5两者均逐渐减小，其中芯层压缩量由配置1的45.2 mm减小为配置5的10.1 mm，减小了77.6%;芯层内能从配置1的84 kJ减小为配置5的9.7 kJ，减小了88.4%。由文献[17]的研究可知，内面板越薄，夹芯结构获得的爆炸能量越多，因而配置1芯层吸收的能量最多，而配置5内面板最厚，因而芯层吸收的能量最少。

由于为圆筒结构，这5种配置夹芯圆筒的重量并不相同，由表4可知，从配置1到配置5的重量逐渐减小，配置1相对于配置5重量增加了8.3%。

图17 不同配置夹芯圆筒的外面板径向变形Fig.17 Radial deflections(outer face-sheets)of sandwich-walled hollow cylinders with different configurations

图18 不同配置夹芯圆筒Fig.18 Comparison of sandwich-walled hollow cylinders with different configurations

由以上分析可知，在2 kg炸药量下，性能优良结构应在配置1、配置2和配置3中选择，即内面板厚度应不大于外面板厚度，在这种情况下内面板容易发生塑性变形，而外面板能起到强的约束作用，使泡沫铝芯层发生塑性压缩，在降低夹芯圆筒整体变形的同时能够发挥泡沫铝芯层的吸能优势;虽然此时夹芯圆筒的重量会有所增加，但重量的增加所换来的是抗爆性能的显著提高。而在配置1、配置2和配置3这3种配置方式中选择最优的配置，或在内面板厚度应不大于外面板厚度的情况下获得最优的内、外面板厚度尺寸，则面临外面板径向变形和芯层吸能这两个相互矛盾的抗爆指标，因此在实际应用中需要确定最主要的抗爆指标，或确定一个合理的综合指标(把各个分指标用合适的比例进行叠加)，据此来确定最优的结构。

4 结论

运用有限元数值模拟，对夹芯圆筒和实体圆筒在爆炸载荷作用下的动力响应进行了研究，分析了其抗爆性能，结果表明:

(1)夹芯圆筒内面板厚度应不大于外面板厚度，这样配置的内、外面板能在降低夹芯圆筒整体变形的同时发挥泡沫铝芯层的吸能优势。

(2)在实际应用中可能会面临相互矛盾的抗爆指标，这就需要确定最主要的抗爆指标，或确定一个合理的综合指标，据此来优化结构。

(3)在相同重量和相同炸药量的条件下，由A3钢与闭孔泡沫铝制成的夹芯圆筒比由A3钢制成的实体圆筒具有更优越的抗爆性能;在变形方面，夹芯圆筒的整体变形小于实体圆筒;在能量方面，夹芯圆筒吸收的内能和转化的动能均大于实体圆筒。

(4)在爆炸载荷作用下，泡沫铝芯层具有消波功能，通过衰减作用降低了外面板的应力水平，能有效避免圆筒结构破裂所造成的二次伤害，增强防爆结构的安全可靠性。

(5)夹芯圆筒相比实体圆筒增加了泡沫铝芯层，增大了圆筒结构的阻尼，能更快消除结构的震荡响应。

(6)在实际应用中，有必要对泡沫铝夹芯圆筒的筒壁与底板的连接部位进行加强以减小应力峰值。

[1]Sriram R，Vaidya U K，Kim J E.Blast impact response of aluminum foam sandwich composites[J].Journal of Materials Science，2006，41(13):4023－4039.

[2]Zhu F，Zhao L M，Lu G X，et al.Structural response and energy absorption of sandwich panels with an aluminium foam core underblastloading[J]. Advancesin Structural Engineering，2008，11(5):525－536.

[3]Zhu F，Zhao L M，Lu G X，et al.A numerical simulation of the blast impact of square metallic sandwich panels[J].International Journal of Impact Engineering，2009，36(5):687－699.

[4]Theobald M D，Langdon G S，Nurick G N，et al.Large inelastic response of unbonded metallic foam and honeycomb core sandwich panels to blast loading[J].Composite Structures，2010，92(10):2465 －2475.

[5]Shen J H，Lu G X，Wang Z H，et al.Experiments on curved sandwich panels under blast loading[J].International Journal of Impact Engineering，2010，37(9):960－970.

[6]石少卿，刘仁辉，汪 敏.钢板－泡沫铝－钢板新型复合结构降低爆炸冲击波性能研究[J].振动与冲击，2008，27(4):143 －146，176.

[7]任新见，张晓忠，李世民.钢板－泡沫金属－钢板叠合结构抗爆机理初探[J].爆破，2009，26(1):25－28.

[8]田 杰，胡时胜，陈 健.次生冲击波超压的实验研究和数值模拟[J].兵工学报，2007，28(12):1483－1488.

[9]韩守红，吕振华.铝泡沫夹层结构抗爆炸性能仿真分析及优化[J].兵工学报，2010，31(11):1468－1474.

[10]Wang C，Chen H R，Hu X Z，et al.Dynamic failure analysis of aluminum foam sandwich structure using 3D material point method[J].Advanced Materials Research，2008，41 － 42:363－367.

[11]赵桂范，王伟东.抗爆炸冲击波的有限元建模[J].振动工程学报，2004，17:731－735.

[12]吴桂英，贾昊凯，周 稳，等.ALE方法模拟爆炸载荷作用下球壳反直观行为[J].振动与冲击，2011，30(6):93－96.

[13]王定贤，王万鹏，石培杰，等.柱形爆炸容器动力学响应的有限元模拟与实验检验[J].压力容器，2008，25(7):13－16.

[14]高轩能，王书鹏.大空间柱面网壳结构在爆炸荷载下的动力响应[J].振动与冲击，2009，28(10):68－73.

[15]高轩能，刘 颖，王书鹏.基于LS-DYNA的大空间柱壳结构爆炸波压力场分析[J].振动与冲击，2011，30(9):70－75.

[16]张 健，赵桂平，卢天健.闭孔泡沫铝应变率效应的试验和有限元分析[J].西安交通大学学报，2010，44(5):97－101.

[17]Fleck N A，Deshpande V S.The resistance of clamped sandwich beams to shock loading[J].Journal of Applied Mechanics-Transactions of the Asme，2004，71(3):386－401.