强载荷下结构动力响应与损伤的跨尺度分析

汤轶群，李兆霞

(东南大学 土木工程学院工程力学系，南京 210096)

整体结构的失效总是起始于局部的损伤累积，然而局部损伤与整体结构是分别处于局部微、细观尺度与整体结构尺度这样两个不同量级的空间尺度上，所以结构损伤失效过程成为一个跨尺度演化的过程。现行结构分析方法多在单一尺度上进行，在结构整体大尺度上，构件局部损伤及其对结构劣化的影响难以准确模拟;为了关注结构中的易损局部细节，若整体精细模拟，则节点数及单元数会非常庞大，使得模拟无法实现或影响计算效率[1－2]。应用跨尺度分析方法可以很好的解决这一问题，同时分析结构响应及其局部易损部位的损伤演化过程。

对大跨结构的整体或局部不同部位的描述，其适用的理论和尺度范围取决于描述目的和主要考察对象。从结构全尺度、局部构件尺度和损伤细节尺度三个方面建立多尺度模型时，各个模型尺度所关注的分析对象、适用的理论以及有限元单元特征长度都应有所不同:① 大型工程结构全尺度，其尺度范围在100～103m，适用结构力学理论，分析结构内力;② 梁、柱、板、壳等构件尺度，其尺度范围在10－3～100m，适用于材料力学、弹性理论，分析构件名义应力;③ 含缺陷的节点细部构造，其尺度范围在10－6～10－3m，适用于宏、细观损伤理论，分析热点应力、损伤演化[2]。

图1以局部构件模型为例，给出了典型的跨尺度(局部构件尺度与细观尺度)有限元模型各组成部分。该等截面梁分别由左边的精细实体单元模型和右边的宏观梁单元模型组成，宏观梁单元模型在整体结构中属于无缺陷且始终处于弹性阶段的部分，而精细实体单元模型的引入是为了分析结构中的缺陷部位。由于应力集中区域的应力梯度较大以及损伤理论的适用范围要求，需要把局部缺陷部位的单元网格细化，于是从宏观的构件尺度到细观的损伤尺度便需要通过跨尺度界面及过渡区域连接起来。在跨尺度界面上，根据研究对象的需要选取相应的单元连接方法，是多尺度有限元建模中的重点内容。

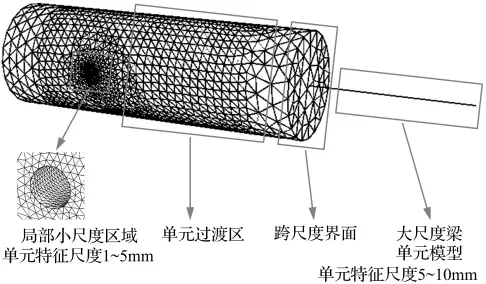
图1 跨尺度模型的基本组成部分Fig.1 The fundamental component of the trans-scale module

目前在有限元软件中实现不同单元间的连接主要有下面三种方法:① 直接写入节点位移约束方程;②建立耦合单元;③ 建立过渡单元[3－14]。这些方法的本质是一样的，都是为了建立不同类型单元间的节点位移关系。文中以以更加灵活、自由的写入节点位移约束方程为例，讨论两种基本的建立方法:① 通过满足两种不同尺度模型在跨尺度界面上的位移协调建立节点位移约束方程;② 通过满足两种不同尺度模型在跨尺度界面上的做功相等建立节点位移约束方程。通过对以上两种单元连接方法的详细对比分析，对于更加方便地建立能够准确反映局部损伤细节的多尺度有限元模型有着十分积极的意义。

配合跨尺度界面上的单元连接方法，本文还在局部小尺度区域引入了塑性损伤耦合的本构模型，真正实现了跨尺度分析。为了验证本文跨尺度分析方法的正确性，以一钢桁架结构为例分别建立多尺度有限元模型和单一尺度精细单元模型配合实验进行验证，并对两种模型进行了抗震分析。计算结果表明，运用本文跨尺度分析方法所建立的多尺度有限元模型能够准确地反映局部节点细节，可以替代单一尺度模型进行强载荷下的结构动力响应与损伤分析，并且能够大大地提高计算效率。

1 跨尺度界面连接方法

在多尺度有限元模型的跨尺度界面上，可以通过节点位移约束方程把不同类型单元上的节点连接起来[15]，约束方程是一种联系自由度值的线性方程，其形式如下:

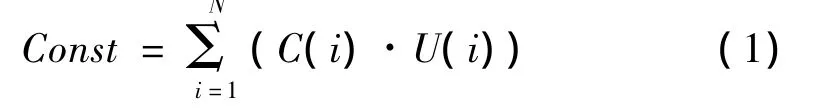
式中:U(i)为节点i的位移自由度项，C(i)为节点i的位移自由度项的系数，N为参与连接的点自由度总数。

1.1 跨尺度界面位移协调方法

如图2所示，在跨尺度界面上小尺度精细单元模型上的某一节点与大尺度梁单元节点之间的位置关系，并在跨尺度连接界面处建立局部坐标系xyz。不同尺度模型在界面上的自由度按照平截面原则进行传递[16－17]。在界面上，以大尺度模型上的节点A为主节点，小尺度模型上的各个节点Bi为从节点，相当于在A点与各个Bi点之间建立一个刚性梁，以保证它们之间的位移协调。针对图2的三维局部坐标系，假设界面的转角很小，可以建立节点位移约束方程如下:

其中:ux，uy，uz分别为 x，y，z方向的位移，rotx，roty，rotz分别为 x，y，z轴的转角。

图2 双尺度模型在跨尺度界面上节点之间关系示意图Fig.2 The relationship between nodes on the trans-scale boundary

为保证跨尺度界面上位移的协调性，恰当的提法应该是要求变形后两种模型在跨尺度界面上各点位移沿垂直于该面方向(即平行于梁单元轴线方向)的分量相同，即两类单元在跨尺度界面上仍然保持贴合，但不能要求两种模型在界面上各点位移沿面内方向(即垂直于梁单元轴线方向)的分量相同，因为梁单元忽略了该方向的位移变化。如果要求两类单元在跨尺度界面内方向上的位移一致，就是强迫小尺度下的精细单元模型在跨尺度界面面内方向的应变为零。这个不恰当的强制条件会使跨尺度界面处的应力分布不同于实际情况，使计算结果失真。因此可以说这是一种刚性的连接方法，该方法要求跨尺度界面要处于线弹性小变形范围内，且要远离局部应力集中区域，以保证所关注的局部缺陷部位的计算结果是比较准确的。

1.2 跨尺度界面应力协调方法

为了满足大尺度下的梁单元与小尺度下的精细单元模型在跨尺度界面处应力的连续性，假设在界面上的做功相等，并按材料力学原理求解界面应力，可推导得到在各种力作用下梁单元与精细单元耦合的多点位移约束方程。其中，小尺度模型在跨尺度界面上的应力分布都是按照材料力学理论在一定假设的基础上推导得出的，所以整个跨尺度界面也是要偏向于杆件属性的，必须符合平截面假定，且处于线弹性、小变形范围内。假如在跨尺度界面上满足了弹性、小变形的假设，便可以根据叠加原理将跨尺度界面连接分成轴向拉压、纯弯曲、剪切、纯扭四种情况，其中纯弯曲和剪切情况在跨尺度界面内又可以分为两个方向，于是便可以得到六个等式。这六个等式分别对应于六种不同的梁单元自由度。等式的具体建立过程如下:

如图3，在轴向拉伸Fz的作用下，小尺度模型在跨尺度界面上只有z向正应力。所以在界面(z=0)处，可以根据做功相等得到下式:

其中:Fz是梁单元的轴力，w为跨尺度界面上梁单元节点的轴向位移，σz为跨尺度界面上小尺度模型的轴向应力，W是小尺度模型在界面上某点的轴向位移(以坐标为自变量的函数)，A为跨尺度界面上小尺度模型总面积。

图3 轴向拉伸作用下双尺度模型在界面上的应力分布Fig.3 The stress distribution on the trans-scale boundary under the pull load

如果研究对象细长，则跨尺度界面处小尺度模型上的轴向应力值为常数:

又因为小尺度模型面上的某点轴向位移可以由已知的各单元节点的轴向位移{W}插值表示出来，单元确定了，形函数〔N〕就可以知道，于是有:

假设小尺度模型在连接界面上涉及到的单元总数为 Nelememt，将式(5)、(6)代入式(4)得到:

其中:Aj为小尺度模型单元j在连接面上的面积。

得到在轴向拉压情况下的多点位移约束方程为:

其中:Wi为在跨尺度界面上小尺度模型单元节点i沿该面法线方向上的位移，Bi为约束方程(9)式中节点位移Wi的系数。

同理，可以得出模型分别在弯矩、剪力、扭转作用下的多点位移约束方程。这种方法是从满足跨尺度界面应力连续性的角度出发，根据功相等导出位移约束方程，条件是要引入相应的应力公式，可以保证应力在跨尺度界面处精确传递，同时也要保证跨尺度界面能符合一定假设条件。

2 两种连接方法的算例分析和比较

以一箱形截面的悬臂梁的自由端在各种方向下受力后的位移分析为例，考察上述两种连接方法的计算效果。该悬臂梁横截面尺寸为15 mm×12 mm，梁长为1 m。材料属性取弹性模量为210 GPa，材料泊松比为0.3。

基于ANSYS有限元软件，分别建立单一大尺度梁单元模型(a)，单一小尺度壳单元模型(b)和双尺度有限元模型(c)，如图4所示。双尺度有限元模型将悬臂梁平均分成两段，左边部份为小尺度精细壳单元模型，右边部份为大尺度梁单元模型。梁单元采用的是beam188，壳单元采用的是shell63，其中双尺度模型在跨尺度界面上分别用上一节描述的两种建立约束方程的单元连接方法进行跨尺度连接。

其中双尺度有限元模型图4(c)分别采用上述两种单元连接方式进行跨尺度连接，即:① 根据位移协调建立位移约束方程的连接，在ANSYS中用CERIG命令，选好主从节点，即可自动建立好刚性连接的约束方程[18];② 根据应力连续建立位移约束方程的连接，需要用CE命令，输入参与方程的位移自由度及其系数、方程常数，该系数需要自己推导并编写相应程序。

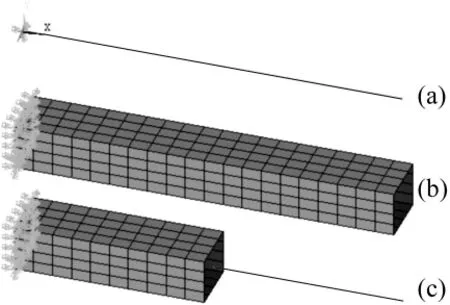
图4 悬臂梁构件的各类有限元模型Fig.4 The cantilever beams with different finite element models

2.1 位移计算结果的比较

分别在悬臂梁自由端六个自由度方向作用载荷，值为10 kN或10 kN·m。以全由beam单元建立的梁单元模型为基准，考察采用两种单元连接方法的双尺度模型自由端在各种载荷作用下的位移及其与梁单元模型的相对误差，计算结果见表1。

表1 多尺度模型与宏观模型在各种载荷下位移结果的比较Tab.1 The comparisons of the displacement values got from different finite elements under different loadings

从表1中可以看出:两种双尺度有限元模型的位移计算结果和单一大尺度梁单元模型很近似，两种双尺度有限元模型之间的差别不是很大。不同于梁单元模型，由于小尺度精细模型在其固定边界上的面内位移被限制及泊松比的存在，会对面外位移产生影响，所以含精细模型边界的双尺度有限元模型的位移计算结果基本要小于单一尺度梁单元模型。由此可见在进行多尺度有限元建模时，模型边界条件的差异也是需要注意的地方。

2.2 应力计算结果的比较

为了考察双尺度有限元模型在小尺度精细单元节点上的应力值，需要用单一小尺度壳单元模型来与这两个采用不同跨尺度连接方法的双尺度有限元模型做比较。在各个模型自由端处作用沿x轴正向拉力10 kN及沿y轴正向剪力10 kN，为了保持和梁单元的受力情况一致以利于比较，将作用力平均分布到自由端节点上，计算后得到的应力分布云图见图5，并给出壳单元模型上不同横截面上所有壳单元节点中面的Mises应力值，见图6。

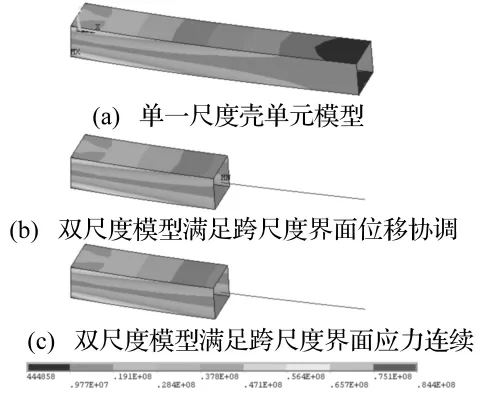
图5 各个模型壳单元中面的Mises应力分布图Fig.5 The Mises stress distribution in different finite element models

从图5可以看出三种有限元模型在精细壳单元模型部分的应力分布基本一致，下面给出精细壳单元模型部分不同横截面上所有壳单元节点中面的Mises应力值，见图6。

图6 三种模型壳单元节点的Mises应力值Fig.6 The Mises stress of different finite element models in different locations

从图5、6中可以看到，三种有限元模型在其精细部分的应力分布基本一致，模型(a)与模型(c)的应力值一直都很相近，模型(b)在跨尺度界面上的应力值较其它两个模型相差较远，但随着距离跨尺度界面越来越远，其应力值也和其它两种模型越来越接近。这是因为模型(b)采用的是满足界面位移协调的约束方法，忽略了小尺度精细模型在跨尺度界面上的面内位移，导致其应力值产生误差，但根据圣维南原理，在其远离跨尺度界面的地方，其应力值应该是比较准确的，这也符合上面的计算数据。模型(c)采用的是满足跨尺度界面应力连续的连接方法，该方法的出发点就是要保证跨尺度界面处的应力值准确，这也符合了上面的计算结果。如图6中所示，当横截面距离跨尺度界面15 cm时，三种有限元模型在此处的应力值已经几乎一致了，而此悬臂梁横截面的最大尺寸也是15 cm，说明了在引用满足跨尺度界面位移协调的连接方法时，跨尺度界面与所关注部位之间的过渡区尺寸最好能达到梁构件横截面的最大尺寸。

通过前面对两种跨尺度单元连接方法的详细比较分析，使我们可以更好地把握对该方法的运用。综合考虑后，满足跨尺度界面位移协调的约束方程地建立要方面许多，且当留有适当的过度区后，我们所关心的应力值也相当精确。于是，本文的跨尺度分析方法在以后的各类计算分析中，都选用满足跨尺度界面位移协调的节点位移约束方法进行跨尺度单元连接。

3 刚节点构件损伤多尺度分析

为了进一步考察跨尺度分析方法，在大型有限元软件ABAQUS进行考虑材料损伤演化的结构动力响应有限元分析，将以抗震结构的典型构件——狗骨式刚节点在强动载荷下的损伤分析为例。在狗骨式刚节点的地震响应分析过程中引入材料损伤，利用UMAT子程序[19]，写入Lemaitre应变－损伤耦合本构模型和损伤演化方程[20－21]，分析材料损伤对低周反复载荷下狗骨式刚节点抗震性能的影响及考虑材料损伤时刚节点构件的失效过程与破坏模式。建立多尺度模型，比较全实体单元的精细模型与多尺度模型的损伤分布计算结果及其计算时间，来说明多尺度模型在结构损伤计算中的可行性及其在计算效率上的优越性。

3.1 算例结构的几何模型

作为改善钢框架结构抗震性能的主要节点形式之一，狗骨式节点设计原理是采用削弱梁翼缘截面方式来降低梁的抗弯能力，削弱部分起到保险丝的作用，使塑性屈服在梁削弱位置出现并扩展，避免节点过早出现裂缝，相对而言等于提高了节点延性和抗弯能力。

为确定圆弧狗骨式节点的截面削弱区位置及尺寸，美国 FEMA(Federal Emergency Management Agency)推荐了该类节点的设计方法。圆弧型翼缘削弱节点的设计参数如图7所示，b为起始削弱点距柱表面距离，c为削弱宽度，a为削弱深度。削弱部位宽度c主要由延性和刚度要求确定，削弱深度a的取值须保证最大削弱截面成为破坏控制截面，b的取值必须满足节点的构造要求。几何模型尺寸见表2

图7 狗骨式节点几何参数示意图Fig.7 The physical dimensions of the dog-bone frame joint

表2 钢框架狗骨式节点梁柱截面尺寸/mmTab.2 The physical dimensions of the dog-bone frame joint/mm

在有限元模型中，柱高和梁长均取为3 600 mm。综合圆弧形狗骨式刚节点的削弱截面尺寸要求，取a=50 mm、b=125 mm、c=450 mm、R=535 mm，节点区形状可参照图7。

3.2 材料损伤本构及其参数

Lemaitre弹塑性损伤耦合本构理论适用于描述金属延性损伤特性对其应力应变关系的影响，且只需改变损伤演化方程，即可引入不同金属材料的损伤本构方程完成计算。用弹性模量表示损伤变量时，可以应用完备形式的三维Lemaitre损伤演化动力律(10)式描述钢材的损伤特性。

损伤演化动力律:

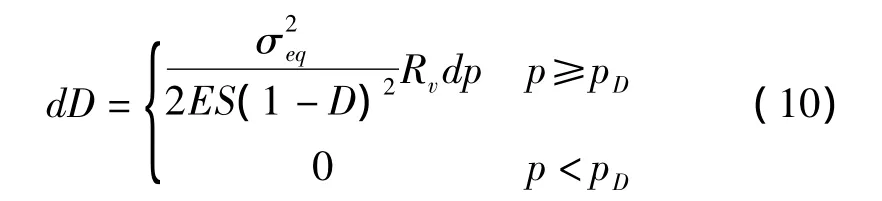
若有D=Dc，并且有，则裂纹萌生。式中的材料参数必须通过材性实验和损伤度量来确定:D:损伤变量;S:损伤的能量强度;Pd:与材料和载荷有关的损伤门槛函数;σu:材料的极限强度;Dc:临界损伤。

在结构分析中，假设当局部应变大于材料极限应变时该处材料达到极限强度，随后该处材料会发生塑性流动变形和颈缩破坏;当材料达到极限应变时，损伤也达到其极限值。本文选取了Von Mises屈服准则和混合强化模式，考虑Q235钢的材性实验以及其塑性硬化规律实验结果，可以得到弹塑性材料性能指标:弹性模量E=200 GPa，泊松比 v=0.3，屈服强度 σy=235 MPa，随动强化模量Hk=1 100 MPa，混合强化系数h=0.2。除了弹塑性材料性能指标外，还需要通过材料的损伤度量实验确定Lemaitre损伤演化方程中的材料常数。现有资料中可以将Q235钢的损伤应变门槛值取为εpd≈0.01，将结果推广到三维条件下，可以认为累积塑性应变值达到0.01时损伤起始。综合宋振森的损伤实验结果和Lemaitre理论中损伤能量强度S的计算方法，考虑Q235钢达到强度极限时塑性应变极值为εu=0.15可以确定Q235钢临界损伤值为D1C，其损伤能量强度 S=0.281 MPa[22－24]。

3.3 UMAT子程序实现流程

ABAQUS中用户材料子程序UMAT的开发主要解决两方面问题:本构模型建立和积分算法选择。本文在UMAT中应用完全隐式向后Euler法的径向返回方法，考虑了平衡迭代的收敛和计算结果的正确性，用程序形式写出了Lemaitre损伤塑性理论(图8)。结构的弹塑性行为与加载以及变形的历史有关，一般使用增量载荷法计算，对每一载荷增量，将弹塑性方程分步线性化，从而使得弹塑性分析这一非线性问题分解为一系列线性问题。

UMAT子程序的主要功能是根据程序定义的材料本构方程，由主程序传入的应变增量求解应力增量，更新积分点处的应力应变状态，提供雅克比矩阵(Jacobian)给ABAQUS主程序以形成下次迭代时的单元切线刚度矩阵和结构整体刚度矩阵。

图8 应用UMAT子程序实现损伤本构描述的流程图Fig.8 The flow chart of introducing meso-damage equation and coupled calculation of stresses with damage evolution in the subroutine UMAT

3.4 有限元模型的建立及结果

对于单一小尺度实体单元模型，考虑各类型单元的特性和本文进行的弹塑性损伤分析要求，为最大程度地保证计算准确性，选用实体单元C3D20R进行计算。对于多尺度模型，把局部薄弱易损伤区域用实体单元C3D20R模拟，通过上一节中的计算分析可知，为了保证缺陷部位计算的精度，多尺度模型用实体单元模拟的精细部分在跨尺度界面和薄弱部位之间要给予适当的过渡区域，该区域的长度最好能取梁横截面的最大尺寸。由于应用损伤理论来分析模型的缺陷部位，所以要保证在缺陷部位的实体单元的特征尺寸在1～5 mm范围内。多尺度模型的其它非重要部分采用梁单元B31来模拟，梁单元模拟部分由于一直处于线弹性阶段，所以采用线弹性本构关系。多尺度有限元模型的跨尺度界面采用耦合的方法将两种尺度模型连接起来，耦合类型为kinematic，该类型耦合方法与本文列举的满足跨尺度界面位移协调的约束方法类似。

有限元模型(a)共有19 733个节点，实体单元C3D20R共有2 964个，有限元模型(b)共有12 497个节点，其中实体单元C3D20R共有1 920个。所以，多尺度模型相对于单一小尺度精细模型节省了近1/3的节点数量和单元数量。

边界条件及加载条件:见图9，在刚节点中柱底面的x、y、z方向设置位移约束，在柱顶面x、z方向设置位移约束，在梁端控制y方向位移。首先通过单向载荷下刚节点的响应分析，可以确定该削弱截面处开始进入塑性时，y方向的屈服位移Δy=0.025 m。

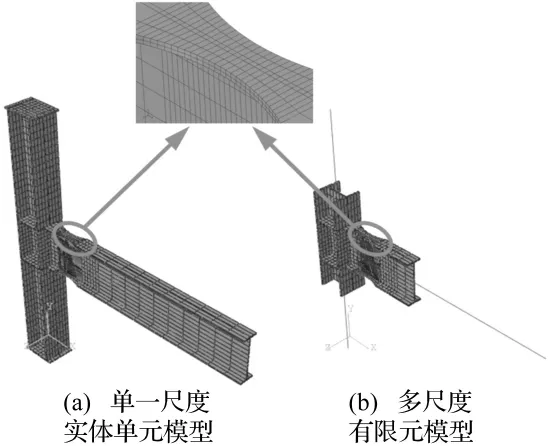
图9 狗骨式节点有限元模型及其薄弱处的单元网格Fig.9 The finite element model of the dog-bone frame joint

考虑了《建筑抗震试验方法规程》(JGJ101－96)相关要求，采用ECCS完全加载制度，加载时梁端位移按以下方式进行:

要确定节点关键截面处梁翼缘全截面材料的累积塑性应变是否达到了极限值，可以根据文献[23]的实验结果，在刚节点构件损伤过程和抗震性能分析中，认为梁削弱处全截面累积塑性应变值达到0.15时，构件失去承载能力;梁削弱处全截面累积塑性应变值达到0.25时，构件发生破坏。刚节点在低周反复加载的计算分析过程中，每一周加载到极限值时所用的分析时间设为1 s。经过计算，加载过程中当Δ=2Δ+y(t=5 s时刻)开始，累积塑性应变达到损伤起始值，刚节点梁部分削弱程度最大截面翼缘处的材料损伤开始萌生和演化;当加载位移由3Δy增至4Δy后，梁削弱处全截面累积塑性应变达到极限值，载荷作用下截面削弱处较长梁段材料均进入塑性并产生不同程度的损伤。于是，刚节点梁端作用的位移低周反复载荷在第一次达到4Δ+y时停止，一共循环了6周半，总共分析时间为13 s。比较单一小尺度实体单元模型与多尺度有限元模型在加载到13 s时，两种有限元模型在局部处的损伤分布，见图10。

图10 采用两种模型计算得到的损伤分布状况Fig.10 The damage distribution on vulnerable areas in two different finite element models

从图10中可见两种模型计算得到的损伤分布基本一致，刚节点梁部分削弱程度最大截面的翼缘外侧的损伤量最大，且表现出此时狗骨式刚节点的材料损伤主要分布在梁削弱截面处，翼缘削弱程度越大则损伤量越大。为了比较两种狗骨式刚节点有限元模型加载各阶段在梁截面削弱处损伤演化的具体差异，从加载时间的第5 s、刚出现损伤开始，列出模型(a)、(b)在各时刻的损伤最大值，也即翼缘削弱程度最大处的损伤值，见表3。

表3 两种模型计算得到的损伤值Tab.3 The comparisons of damage values got from two different finite element models

从上表可以得到，两种模型在加载过程中，损伤增量越来越大，损伤演化速度加快;除去损伤刚开始不久5 s时的损伤值，两种模型相同位置处损伤值之间的相对误差也越来越大，这是可能是由于载荷幅值不断加大以及计算误差不断累积造成的。尽管两种模型之间存在一定的计算误差，多尺度有限元模型依然能够准确地估计狗骨式刚节点薄弱区域的损伤起始时间，准确地反映薄弱区域的损伤演化及分布情况。在加载的最后时刻，两类有限元模型在刚节点梁削弱处的损伤值误差达到最大，但基本可以确定是在刚进入4Δ+y位移加载循环时达到承载极限。

在同一台电脑上，(a)、(b)两种模型的计算时间比较:

(a) 模型的CPU运行时间:2 353.5 s

(b) 模型的CPU运行时间:1 525.1 s

从对比可以看出，(b)模型的CPU运行时间相对于(a)模型节省了近1/3的时间，大大提高了计算效率。通过此次狗骨式刚节点考虑材料损伤演化的计算分析对比，多尺度有限元模型总体上的损伤分布情况基本和单一尺度实体单元模型一致且计算结果相差不大。因此，可以认为在进行强载荷作用下钢构件的动力响应和损伤分析时，引用跨尺度分析方法不仅可行而且可以提高计算效率。

4 钢桁架结构的损伤跨尺度分析

为了进一步探索跨尺度分析方法在结构损伤分析中的应用，并尽量避免由于结构模型复杂而对计算结果准确性造成的不可预知影响，本文分析了具有代表性的某大跨悬索桥钢箱梁纵向加劲钢桁架结构，分别建立单一小尺度精细单元模型和多尺度有限元模型并对比它们的静力响应、动力特性以及强载荷下的非线性动力响应和计算效率。该结构中的构件截面特点和尺寸都比较规则，也具有一定的工程应用典型性。

在大跨桥梁结构中，其钢箱梁结构形式非常有代表性，选取其中纵向加劲桁架结构的典型标准段按照1∶5的比例制作了缩尺实验结构试样。缩尺结构试样的主要结构尺寸、焊缝形式、加工工艺等均以与原桥钢箱梁纵向加劲桁架原型实际相似为准则，材料为普通Q235钢，整个模型高1.32 m，长4.2 m，焊接钢桁架试验系统实体图见图11。

图11 焊接钢桁架结构试验系统实体图Fig.11 The testing system of the welding steel truss

4.1 多尺度有限元模型的建立

在整个刚桁架结构中，有很多地方是符合梁单元特性的，且在加载过程中始终不会有损伤产生，属于不需要关注的部位。于是，针对这样的情况可以选择跨尺度分析方法来模拟整个刚桁架结构，将可能发生损伤的局部缺陷部位用适用于小尺度损伤分析的实体单元来模拟，不发生损伤且符合梁单元特性的部分用适用于大尺度分析的梁单元来模拟。

根据对跨尺度界面的要求和圣维南原理，小尺度局部节点区域在应力集中区域和跨尺度界面之间要留有一定的过渡区域，以防止由于局部应力集中对跨尺度界面产生影响，引起计算结果产生误差;在本例中，对于易发生损伤的梁附近留有沿梁长方向0.15 m的过渡区域(0.15 m为该加劲钢桁架结构梁的最大尺寸)，为了保险起见，对于没有发生损伤的节点区域也沿梁长方向留有0.1 m的过渡区域，以保证模型的计算精度。建立好后的多尺度有限元模型包含了59 980个节点，8 412个C3D20R单元。没有采用跨尺度分析方法的单一小尺度实体单元模型包含了72 656个节点，10 406个C3D20R单元，见图12。

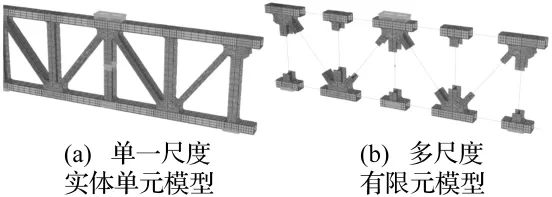
图12 钢桁架结构的两种有限元模型Fig.12 Two different finite element models of the steel truss

4.2 实验验证及对比

为了对比本文所建的单一小尺度实体单元模型和多尺度有限元模型、并将它们与实验数据做比较，验证这两种模型的准确性，根据实验工况加载(见图11)，计算了在200 kN载荷作用下，两种模型在图13中测点位置上(虚线位置)的应变分布特性。

计算后，得到钢桁架结构在200 kN载荷作用下，(a)、(b)两种模型与应变分布实验在测点位置的应变值分布，见图14。

图13 应变分布实验测量位置Fig.13 The locations of the strain distribution test

图14 两种有限元模型与应变分布实验在测点位置处的应变值分布Fig.14 The strain values got from the finite element models and the test in different locations

从图14中，发现单元小尺度实体单元模型与多尺度有限元模型之间的计算结果差别很小，可以证明多尺度有限元模型可以替代单一小尺度实体单元模型进行静载荷下关注局部热点应力、应变分布的计算分析。有限元模型计算得到的应变值与实验测得的应变值相对于测点位置的变化趋势是十分吻合的。但是，数值模拟得到的结果与实验结果相比整体偏小，这主要是由于数值模型及载荷、位移边界条件都无法还原真实情况造成的。

分别用单一小尺度实体单元模型和多尺度有限元模型计算钢桁架结构的整体一阶弯曲振型频率和局部斜向构件一阶弯曲振型频率并做比较(见图15)，考察多尺度模型替代单一尺度模型进行动力特性分析的可行性。再用两种模型的数值模拟结果来对比实验测试结果(见表4)。

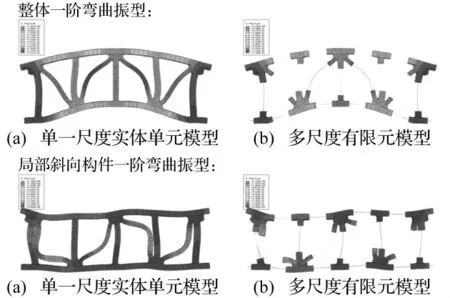
图15 加劲钢桁架结构两种有限元模型的振型图对比Fig.15 The vibration modes of the two different steel truss finite element models

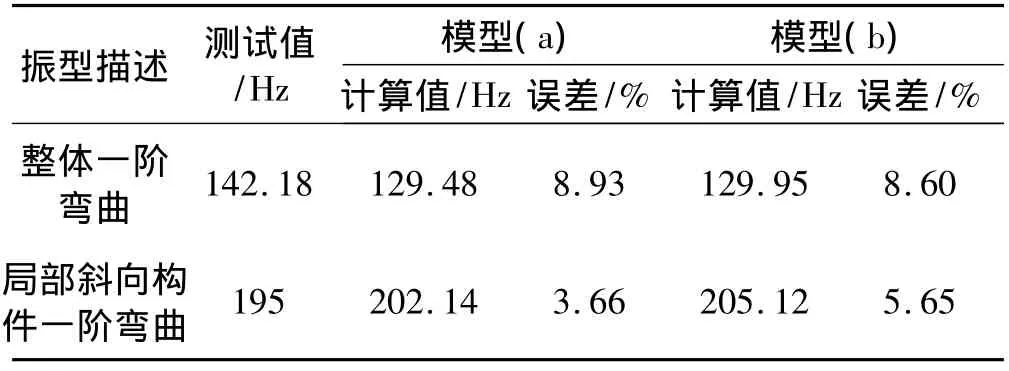
表4 钢桁架结构实验测试和两种有限元模型模拟的固有频率对比Tab.4 The comparisons of steel truss natural frequency got from two different finite element models and the test

从图15的两种模型振型图对比和表4的各项数值可以看出，多尺度有限元模型和单一小尺度实体单元模型的相似度很高，虽然前者相对于后者使用了大量梁单元来替代实体单元，但是通过结构整体一阶弯曲振型及它们频率值的对比，可以证明两种模型的质量及刚度分布一致，通过局部斜向构件一阶弯曲振型及它们的频率值的对比，可以证明多尺度有限元模型可以替代单一尺度实体单元模型识别结构局部损伤状态。通过对应振型固有频率的数值计算结果与实验测试结果的对比，发现它们之间的相对误差均在10%以内，两种结果比较接近，可以认为单一小尺度实体单元模型和多尺度有限元模型计算出的结构动力特性比较符合实际情况。

4.3 钢桁架结构的动力响应与损伤跨尺度分析

为分析低周反复载荷下钢桁架结构的损伤失效过程，根据本文3.3节中介绍的用于抗震分析的ECCS完全加载制度施加位移控制载荷，当结构危险点处累积塑性应变达到极限值而导致该位置处材料失去承载能力时结束加载。载荷施加方式与模型边界条件如图12所示，钢桁架两边底部的节点施加固定约束，位移控制载荷施加在钢桁架中部的顶端节点、腹杆中部及底端节点三处。

通过单向载荷下钢结构的响应分析，可以确定钢桁架结构节点薄弱区域开始进入塑性时，其加载方向y方向的屈服位移Δy=0.002 m。在进行低周反复载荷下钢桁架结构的动力响应与损伤分析时，循环一周的时间仍按2 s计，载荷分析步时间初设为0.05 s。

通过计算，钢桁架单一小尺度实体单元模型在位移载荷第一次达到4Δ+y时，其最大累积塑性应变达到0.15，该位置处材料失去承载能力，加载停止，总共加载过程历经时间13 s，269个载荷分析步。钢桁架多尺度有限元模型在位移载荷接近4Δ+y时(12.96 s)，其最大累积塑性应变达到0.15，为了便于与单一小尺度实体单元模型对比，也计算到13 s，总共经过了268个载荷分析步。加载完成后，对比整体结构上所有的损伤区域，损伤值比较大的区域都出现在钢桁架结构的下端。给出两种模型最后时刻危险点(塑性和损伤累积程度最高处)区域的损伤分布情况(见图16)及在危险点处各个加载时刻的损伤值(见表5)。

通过上面的对比可以发现两种模型在最后时刻的损伤区分布一致，各个加载时刻的损伤值也十分接近。虽然两者之间的计算结果会随着加载过程不断增大，但它们最终的误差不大，且多尺度有限元模型估计的损伤起始时刻及危险点处材料的承载力失效时刻都和单一小尺度实体单元模型估计的几乎一致。此次计算，单一小尺度实体单元模型一共经历了269个载荷分析步、6 656.9 s的计算时间，多尺度有限元模型一共经历了268个载荷分析步、4 120.3 s的计算时间。跨尺度分析方法在此次模拟地震载荷下的结构动力响应与损伤分析中节省了38%的计算时间，体现出了极大的优越性。

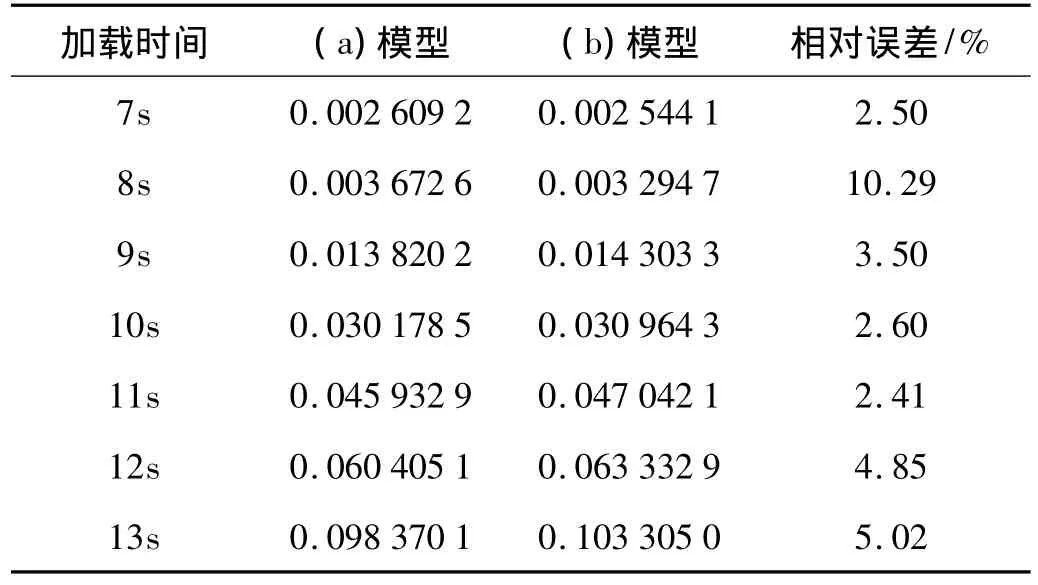
表5 两种模型计算得到的危险点处损伤值Tab.5 The comparisons of damage values got from two different finite element models

图16 低周反复载荷完成后钢桁架有限元模型在危险点处的损伤区分布Fig.16 The damage distribution in the steel truss under ECCS cyclic loading

5 结论

由本文的研究可得到以下结论:

(1)从应用角度考虑，满足跨尺度界面位移协调的约束方程的建立过程比较简单、易于实现程序化，而满足跨尺度界面应力协调的约束方程的建立过程比较繁琐、实现起来比较麻烦。且两种跨尺度界面连接方法成立的条件都是是跨尺度界面所在位置要满足弹性小变形以及相关的梁单元假设，因此，跨尺度界面必须远离塑性区或者损伤区才能应用于损伤非线性分析。

(2)狗骨式刚节点的多尺度有限元模型与单一小尺度实体单元模型在多步计算以后，其损伤累积值差别不大，且各阶段损伤分布基本一致。通过两种模型的计算时间比较，多尺度模型替代单一小尺度精细模型可大大提高计算效率。虽然本文分析的构件的计算规模较小，但可以预见，所分析的结构计算规模越大，可节省的计算时间就会越多。

(3)本文建立的钢桁架结构多尺度有限元模型是比较成功的，在静动力分析中都能很好的近似单一小尺度实体单元模型，且都接近实验测试结果，具有较高的可信性。文中的跨尺度分析方法在结构动力响应和损伤分析中的应用，实现了强载荷下由材料损伤劣化引起构件和结构局部失效的模拟，更准确地描述了强动载荷作用下结构中由于材料损伤演化导致结构的非线性响应和局部失效的过程，进一步解释了强动载荷下发生的从材料损伤到构件节点失效再到结构破坏的机理。而且应用该跨尺度分析方法建模比较方便，且可以提高分析效率，在不失精度的前提下，体现了极大的优越性和应用前景。

[1]吴佰建，李兆霞，汤可可.大型土木结构多尺度模拟与损伤分析—从材料多尺度力学到结构多尺度力学[J].力学进展，2007，37(3):321 －336.

[2]李兆霞，孙正华，郭 力，等.结构损伤一致多尺度模拟和分析方法[J].东南大学学报(自然科学版)，2007，37(2):251－260.

[3]李兆霞，王 滢，吴佰建，等.桥梁结构劣化与损伤过程的多尺度分析方法及其应用[J].固体力学学报，2010，31(6):731－756.

[4]孙正华，李兆霞，陈鸿天，等.考虑局部细节特性的结构多尺度模拟方法研究[J].特种结构，2007.3，24(1):71－75.

[5]Monaghan D J，Doherty I W，McCourt D，et al.Coupling 1D beam to 3D bodies[C]. 7th InternationalMeshing Roundtable. Sandia National Laboratories， Dearborn，Michigan，1998:285－293.

[6]McCune R W，Armstrong C G，Robinson D J.Mixed dimensionalcoupling in finite element models[J].International Journal for Numerical Methods in Engineering，2002，49:725－750.

[7]Shim K W，Monaghan D J， Armstrong C G. Mixed dimensional coupling in finite element stress analysis[J].Engineering with Computers，2002，18:241 －251.

[8]Surana K S.Transition finite elements for axisymmetric stress analysis[J].International Journal for Numerical Methods in Engineering，1980，15:809 －832.

[9]Surana K S.Transition finite element for three dimensional stress analysis[J].International Journal for Numerical Methods in Engineering，1980，15:991 1020.

[10]Garusi E，Tralli A.A hybrid stress-assumed transition element for solid-to-beam and plate-to-beam connections[J].Computers and Structures，2002，80:105 －115.

[11]Kim H S，Hong S M.Formulation of transition elements for the analysis of coupled wall structures[J].Computers and Structures，1995，57(2):333－344.

[12]McCune R W，Armstrong C G，Robinson D J.Mixed dimensionalcoupling in finite elementmodels [J].International Journal for Numerical Methods in Engineering，2000，49:725－750.

[13]Wenzel M.On dimensional adaptivity for mixed beam-shellstructures[J].PAMM-Proc.Appl.Math.Mech，2004，4:382－383.

[14]Chavan K S，Wriggers P.Consistent coupling of beam and shell models for thermo-elastic analysis[J].International Journal for Numerical Methods in Engineering，2004，59:1861－1878.

[15]王勖成.有限单元法[M].北京:清华大学出版社，2003.

[16]陆新征，林旭川，叶列平.多尺度有限元建模方法及其应用[J].华中科技大学学报(城市科学版)，2008，25(4):76－79.

[17]林旭川，陆新征，叶列平.钢－混凝土混合框架结构多尺度分析及其建模方法[J].计算力学学报，2010，27(3):469－475.

[18]ANSYS Release 10.0，ANSYS Inc.，2007.

[19]ABAQUS Theory Manual[M].ABAQUS，Inc，2006.

[20]Lemaitre J.A Course on damage mechanics[M].Spring-Verlag，1992.

[21]Lemaitre J，Desmorat R.Engineering damage mechanics[M].Springer-Verlag，2005.

[22]罗邦富，魏明钟，沈祖炎.钢结构设计手册(第二版)[M].北京:中国建筑工业出版社，1989.

[23]张 莉.钢结构刚性梁柱节点抗震性能的研究[D].天津:天津大学，2004.

[24]宋振森.刚性钢框架梁柱连接在地震作用下的累积损伤破坏机理及抗震设计对策[D].西安:西安建筑科技大学，2001.