有限维Jacobi 算子特征值的连续依赖性

杜保营

(宜宾学院数学学院，四川 宜宾 644000)

Jacobi算子是一类非常重要的差分算子，有关Jacobi算子的谱理论的研究起步较早并且理论也基本完善成熟，但有关算子的逆谱理论的研究却相对来说起步较晚且有待完善.本文对一类比较简单的 Jacobi算子——有限维 Jacobi算子的逆谱理论的一个侧面进行探讨，即对有限维Jacobi算子特征值的连续依赖性进行探讨.

1 预备知识

定义1［1］设Z为整数集，I⊆Z，M是一数域，符号l(I，M)表示从I到M-值序列，即:

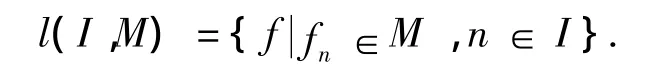
当M=C时，M可以省略.即

l(I)=l(I，C).

若M是Banach空间，我们引入如下定义:

定义2［1］设1≤p ＜ ∞ ，则:

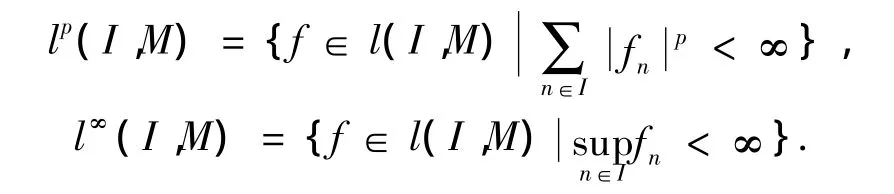
当M是Hillbert空间时，在l2(Z，M)上引入以下内积:

按照以上定义的内积，则l2(Z，M)也是一Hillbert空间.

定义3［2］设 {an}∈l∞(Z，R)，an≠0 ，n∈Z;{bn}∈l∞(Z，R)，n∈Z，则差分算子H:

称为Jacobi算子.其中，H如下定义:

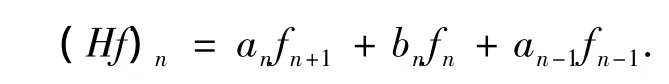
其中，数列{an}、{bn}称为 Jacobi算子 H的系数.

定义 4［3］设 n1＜ n2，定义在 l2［n1+1，n2-1］且在端点处满足齐次Dirichlet边值条件的Jacobi算子称为有限维Jacobi算子，记为 Hn1，n2，即:

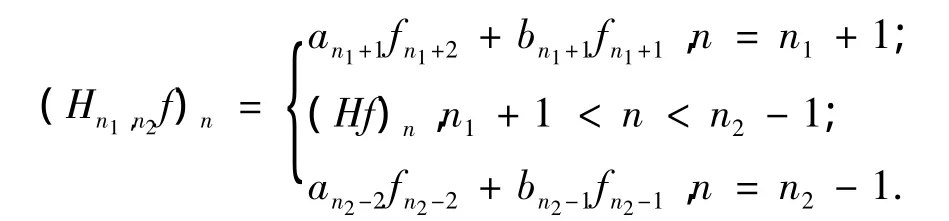
引理1［2］任何一个差分算子R(不妨设定义在空间 l2(Z)上)都对应唯一一个矩阵(R(m，n))m，n∈Z.这里 R(m，n)=Rδn(m)=〈δm，Rδn〉. 其 中， δn(m) = δ(m，n) =是空间l2(Z)上的标准基.

引理2［2］有限维Jacobi算子是有界自伴随算子.

引理3［3］若H是Hillbert空间上的有界自伴随算子，则H的所有特征值是实的.

2 有限维Jacobi算子特征值的连续依赖性

定理1 有限维Jacobi算子Hn1，n2的特征值连续依赖于{an}、{bn}.其中，{an}、{bn}是有限维 Jacobi算子 Hn1，n2的系数.

证明 对于有限维 Jacobi算子 Hn1，n2，为了表示的简单，不妨设n1=0，n2=N+1，则:

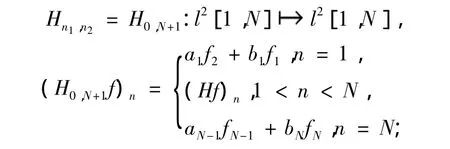
则由引理1知H0，N+1对应的矩阵为:

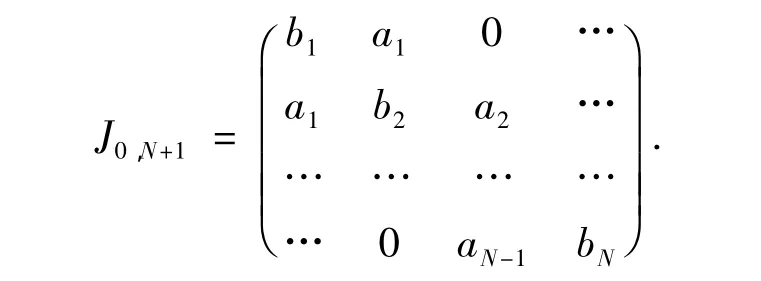
显然，J0，N+1为N阶方阵，对应的特征多项式为:，(I为N阶单位矩阵).

由代数基本定理知［4］:该特征多项式有N个根(特征多项式是一个关于λ的N次多项式).由引理2和引理3知:的这N个根均为实根，不妨设为λ1≤λ2≤…≤λN.

其中，g0，g1，…，gN-1是实数域上的2N-1元连续函数.又由于λ1，…，λN是特征多项式的N个根，所以该特征多项式的系数可以用λ1，…，λN来表示，即

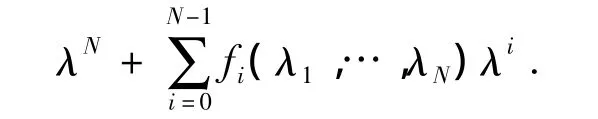
其中，f0，f1，…，fN-1是实数域上的 N元连续函数.所以

构造N个3N-1元连续函数Fi(x1，…，xN-1，y1，…，yN，z1，…，zN).其中:

显然，Fi是实数域上的3N-1元连续函数，且函数 Fi在点 P(a1，…，aN-1，b1，…，bN，λ1，…，λN)处的函数值为零.即:

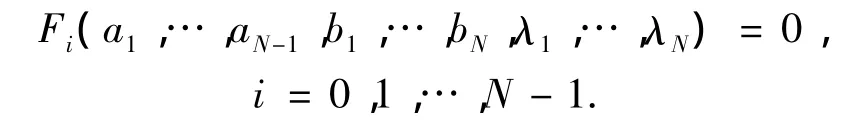
又由于函数Fi在点P的某邻域内具有连续偏导数(Fi是实数域上的3N-1元连续函数)，且

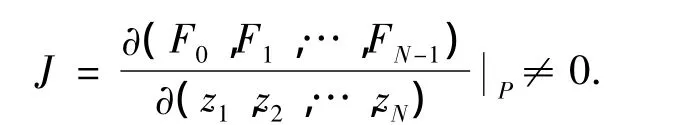
所以，由隐函数存在定理［5］知在点P的某邻域内存在唯一一组函数:

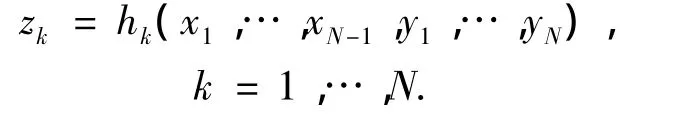
其中:

hk(a1，…，aN-1，b1，…，bN)= λk，k=1，…，N;并且函数 hk(k=1，…，N)在点 (a1，…，aN-1，b1，…，bN)的某邻域内连续，所以λk(k=1，…，N)连续依赖于 a1，…，aN-1，b1，…，bN.即:有限维Jacobi算子的特征值具有连续依赖性，连续依赖于该Jacobi算子的系数.

3 结语

对于无穷维Jacobi算子的特征值的连续依赖性，本文没有做探讨，不过，无穷维Jacobi算子的特征值的连续依赖性和本文所探讨的有限维Jacobi算子其特征值具有连续依赖性有相似之处，不过也有自身的特点和难度，这有待于在以后的研究中解决.

［1］张恭庆，林源渠.泛函分析讲义［M］.北京:北京大学出版社，1986:78-80.

［2］Eschl G T.Jacobi operators and completely intergrable nonlinear lattices［J］.Math.Surv and Mon，Amer.Math.，2002，72.

［3］Diplomarbeit zur Erlangung.Trace formulas and inverse spectral theory for finite Jacobi operators［M］.Eingereicht von Johanna Michor Betreut von.Univ.Prof.Gerald TeschlWien，im Mai，2002.

［4］北京大学数学系几何与代数教研室.高等代数［M］.北京:高等教育出版社，1987:26-27.

［5］刘玉莲，傅沛仁.数学分析讲义［M］.北京:高等教育出版社，2001:217-218.