一类微分系统极限环的存在唯一性

袁雪峰，陈海波

(中南大学数学科学与计算机技术学院，湖南 长沙 410000)

关于微分系统极限环的研究，已经有学者取得丰富的成果.例如，文献［1］讨论了如下系统:

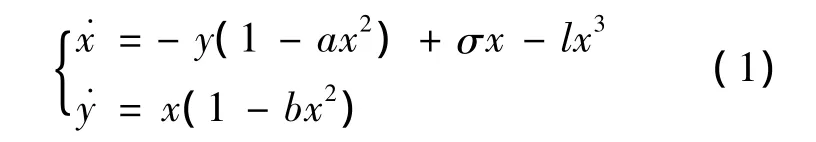
极限环在不同条件下存在的充分条件.

另外，文献［2-4］研究了几类奇次微分系统极限环的问题，特别是文献［5］讨论了更为广泛的系统

极限环的存在性.对于系统(2)，当n=1时，可化为系统(1)，从而知道系统(2)是(1)的推广.文献［2］研究的结果涵盖(1)中极限环存在的条件.

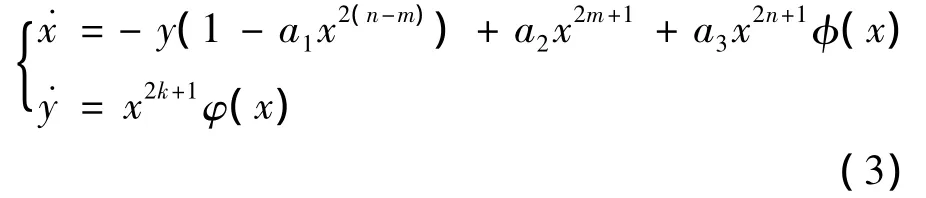
本文是在文献［1-5］的基础上研究了一类广泛的系统的极限环的存在的条件，其中n＞m，2k＞2n-2m+1，n，m，k∈ N，a1，a2，a3是实数，且φ(x)，φ(x)满足以下条件:

(H1)φ(x)为偶函数，且φ(0)＞0;

(H2)xφ'(x)＞ 0;

(H3)φ(x)是偶函数，且φ(x)＞0.

注:(H1)、(H2)包含了φ(x)≥φ(0)＞0.

显然，文献［1-5］所研究的系统都可以作为本文系统的特殊情况.本文对参数a1，a2，a3进行讨论，运用Poincare切线法［6］以及N.Levinson-O.K.Smith定理［7］证明系统(3)极限环的不存在性、存在性和唯一性.

1 引理(Poincare切线法)［6］

F(x，y)=C 是一曲线组，且 F(x，y)∈C'(G)，

2 极限环的不存在性

本节利用不相交定理和引理讨论系统(3)在满足定理给定条件下，其极限环不存在，从而给出极限环不存在的充分条件.

定理1 当a2a3≥0时，系统(3)不存在极限环.

证明 针对定理所给出的条件，对a1=0，a1＜0，a1＞0三种情况进行讨论.

(i)当a1=0时，系统不存在极限环.

当a1=a2=a2=0时，系统化为下面系统

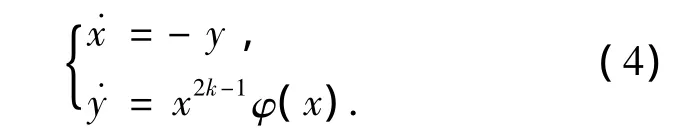
由文献［1］知，O(0，0)是(5)的中心.

用类似上面的方法把系统(3)化为:

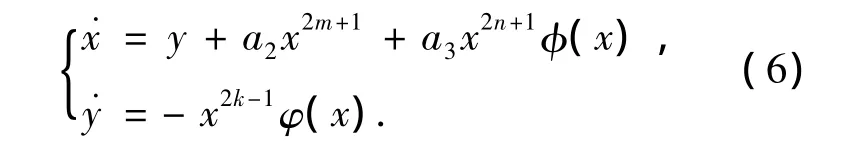
当a2a3≥0时，

故上式为常号，系统(4)和(5)的向量场关于参数a2构成广义的旋转向量场.由不相交定理可以得到这两个系统的闭轨线必定不相交，这与原点是(5)的中心矛盾，即不存在闭轨线，所以当a1=0时，系统(3)不存在极限环.

(ii)当a1＜0，a2a3≥0时，系统(3)不存在极限环.

其中，F(x)，g(x)∈C(-∞，+∞)，又因为a1＜0，所以O(0，0)是唯一奇点.

当x≠0，a1＜0，a2a3≥0时，

又 φ(x)≥ φ(0)＞ 0，

又令

且

故当a2=a3=0时，O(0，0)是中心;当a2＞0，a3＞0时，0;当a2＜0，a3＜0时，＜0.故在(ii)给出的条件下定号，又由引理可以得到系统(3)不存在极限环.

(iii)当a1＞0，a2a3≥0时，系统(3)不存在极限环.

所以由(i)～(iii)的证明知:在定理1的条件下，系统(3)极限环不存在.

3 极限环的存在唯一性

本节验证系统在定理2给定的条件下，满足N.Levinson-O.K.Smith定理，从而得出系统极限环存在且唯一的充分条件.

定理2 当系统(3)满足a1≤0，a2＞0，a3＜0时，存在唯一且稳定的极限环.

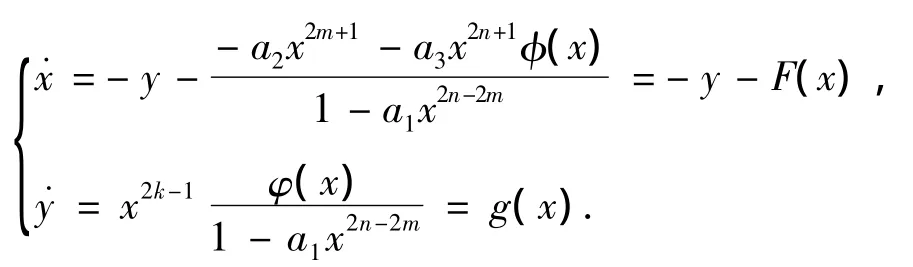
由于a1≤0，所以O(0，0)是唯一奇点.

下面只需要讨论系统在定理2的条件下满足N.Levinson-O.K.Smith定理:

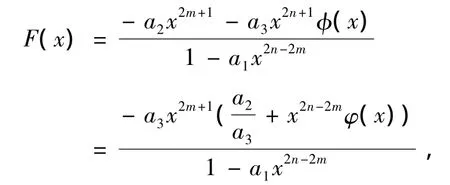
故必定存在x1＞0，使得成立.当0＜x＜x1时，F(x)＜0;当x1≤x时，F(x)≥0;当x1≤x时，-a2≥a3x2n-2mφ(x);有

令

因为a1≤0，a2＞0，a3＜0且xφ'(x)＞ 0，所以

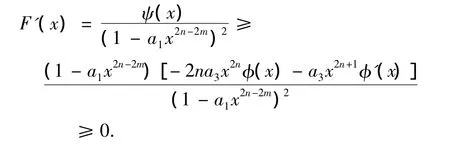
即知当x1≤x时，F(x)≥0且单调递增;

(ⅲ)因2k＞2n-2m+1，a1≤0，故

由(ii)的证明可知:

又

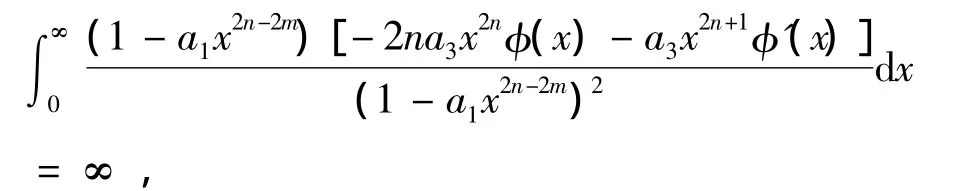
即

(ⅳ)F(x)，g(x)满足Lipschitz条件.

由上面的证明可知，在定理2的条件下，满足定理N.Levinson-O.K.Smith的条件，则系统(3)存在唯一且稳定的极限环.

4 结论

文章研究了一类形如(3)的高次微分系统，对参数进行讨论，利用不同的方法得出了这类系统极限环不存在性、存在性和唯一性的充分条件.这对于高次微分系统极限环的存在性、唯一性的研究起到了一定的推动作用.

［1］梁锦鹏.一类三次系统的极限环［J］.系统科学与数学，2003，23(3):398-404.

［2］Li Jibin，Huang Qiming.Bifurcation of limit cycle forming compound eyes in the cubic system［J］.Chinese Ann.Math Series B，1987，8(4):391-403.

［3］高静，林京.一类奇次微分系统极限环的存在性与唯一性［J］.合肥工业大学学报，2009，32(4):587-590.

［4］马知恩.一类三次系统极限环的存在唯一性［J］.数学年刊 A 辑，1986，7(1):1-6.

［5］张瑞海，张齐.一类多项式微分系统极限环的存在性和唯一性［J］.湘潭师范学院报:自然科学版，2006，28(4):8-12.

［6］张志芬，丁同仁，黄文灶，等.微分方程定性理论［M］.北京:科学出版社，1985:155-231.

［7］叶彦谦，等.极限环轮［M］.上海:上海科学技术出版社，1984:60-135.