活塞数控加工的预期迭代学习控制研究

冯宗杰，王旭东，张金利，黄 华

(第二炮兵士官学校，山东青州 262500)

活塞数控加工的预期迭代学习控制研究

冯宗杰，王旭东，张金利，黄 华

(第二炮兵士官学校，山东青州 262500)

在高速精密非圆加工中，伺服刀架系统的幅值衰减产生较大的刀具轨迹跟踪误差，从而降低加工精度。针对活塞外圆数控加工数据控制，设计了一种预期迭代学习控制方法。推导该控制算法在频域下的收敛条件，经仿真实验验证，这种控制方法运用于活塞外圆加工中可以取得良好的控制效果。

活塞;迭代学习控制;预期学习控制;收敛性

0 引言

活塞作为发动机关键部件，活塞性能的好坏很大程度上取决于活塞的加工精度。随着计算机技术的迅猛发展，设计软件的使用，为了达到最佳效果，活塞的裙部除了通常的中凸变椭圆外，还采用了复杂形状段。复杂截面对活塞数控加工精度的提高增加了难度。国内外研究者目前普遍致力于在一定性能极限内设法提高机床伺服刀架的动态性能的研究［1-3］，而对于在获得相对较好动态性能之后，不同加工参数与伺服刀架动态性能相互影响下对于加工可能造成的误差缺乏定量的研究，导致在实际加工过程中仍然需要多次试凑加工才能确定兼顾效率与精度的加工参数。整个过程费时费力，很大程度上影响了快速伺服车削本应有的高效与柔性。

如何优化选取加工参数，避免经验性或盲目地试凑，如何在保证加工精度的前提下，尽可能地提高加工效率，一直是活塞异型数控加工亟需解决的问题。

本文给出了预期迭代学习控制器，分析了该学习算法的收敛性，并以活塞外圆数控加工作为控制对象进行了仿真验证。

1 非圆截面车削系统和典型的复杂非圆截面

根据具体要求和性能价格比的不同，非圆零件加工系统可以有多种不同的结构和配置。但总的来说，它由车床和伺服刀架及检测控制系统组成。图1是本文构成的一个非圆活塞车削系统的典型配置，它由车床、计算机、横向进给控制系统、高频响直线伺服刀架和检测系统等组成。

图1 非圆截面数控加工系统

直线伺服刀架是加工非圆截面零件最关键的部件，直线伺服刀架安装在车床的中拖板上，它是车刀在工件径向的定位机构;伺服刀架带动刀具在工件的径向作与主轴同步的往复运动，从而使工件形成非圆截面。

位置指令信号是根据被加工的非圆截面的形状和当前刀具相对于工件的位置(主轴编码器的转角)所确定的。非圆截面的形状用某角度上的半径与一个基准圆的半径之差即刀具位移量所确定。图2是非圆车削时曲线形成过程。

图2 非圆车削时曲面形成过程

如图3、4所示分别表示了复杂截面的形状和复杂的截面按角度展开图。通过实验加工，现有设备在加工此形状时将产生很大的误差，不能满足我们的要求。

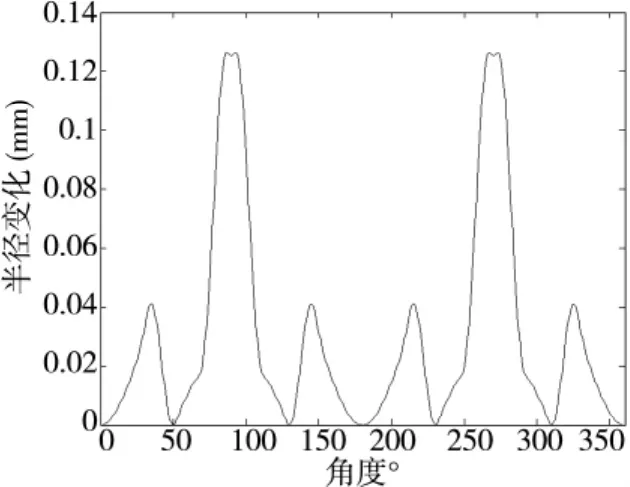
图4 活塞特殊截面按角度展开图

另一方面，输入信号，闭环系统，输出信号是一个完整系统的三部分，控制最终的目的是无误差的跟踪期望信号，故可通过改变输入控制量来提高活塞加工精度，这样可以降低伺服控制系统的难度。

2 迭代学习控制算法

迭代学习控制的任务就是寻求控制输入，使得被控对象的运动轨迹在有限时间区间［0，T］上沿整个轨迹实现完全的零误差跟踪，即实现系统实际输出和期望输出之间的偏差为零，并且要求整个过程要求快速完成。这里的完全跟踪指系统输出自始至终，无论是暂态或稳态，都要保持和目标轨道一致。

2.1 预期迭代学习控制收敛性分析

预期迭代学习控制的主要思想在时域内表现为选择最优的超前时刻误差，修正当前时刻的控制输入，在频域内可理解为引入一相位超前项，抵消对象本身的相位滞后，最大程度地拓宽系统的可学习频段。

在活塞外圆加工中，存在一个问题就是相位滞后，即系统t时刻的输入u(t)事实上对应着t+Δ时刻的输出y(t+Δ)，本文针对活塞数控加工连续系统的滞后问题提出预期学习控制(简称A型ILC)，引入一段Δ时间的超前，从而直接利用t+Δ时刻的误差来修正t时刻的输入，即:

假设SISO离散对象如式(2)所示:

式中，下标k表示第k次循环;Yk表示刀架进给量yk的Z变换;Uk表示控制量uk的Z变换;Wk为测量误差wk的Z变换;Y0k为系统的零输入响应，即它的初态响应。

考虑离散预期学习律:

式中，t=0，Ts，2Ts，…(N-1)Ts;m ＞ 0 为学习的超前步长;γ＞0为学习增益。在离散频域内分析，由Z变换超前定理知，式(3)的Z变换为:

综合上述各式，可得:

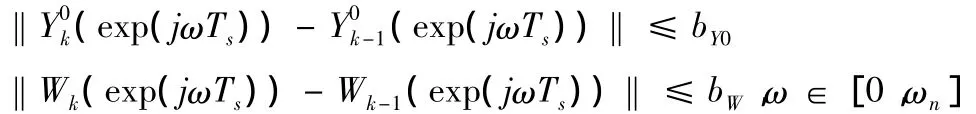
给定的期望轨迹 yd(t)，t∈［0，NTs］，采用(3)所示学习律，则当ρ＜1时:

ωn= π/Ts为 Nyquist频率。其证明在文献［4］中给出。

由式(5)知，当bW=0，bY0=0，即测量噪声和初始响应不随迭代次数改变时跟踪误差

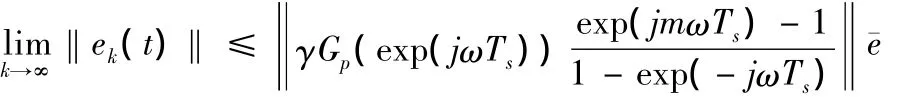
2.2 预期迭代学习算法实现

对于大部分工业系统而言，要保证条件式(6)在ω∈［0，+∞)范围内成立几乎不可能，能保证式(11)成立的频率范围为可学习频带。为使得学习过程中误差不发散，采用截断频率的做法，即假定式(11)在ω∈［0，ωlbw)内成立，其中ωlbw称为最大可学习频率，通过零相位低通滤波ω∈［ωlbw，+∞)的误差信号，相当于不对这部分频率信号进行学习，这导致跟踪误差只能收敛至某个较小的领域(与ωlbw有关，ωlbw越大，越接近零)而不是零。寻找最佳的超前步长和学习增益γ最大化系统的可学习频带成为设计迭代学习控制器的关键。

2.2.1 离散控制器设计

记 Gp(jωTs)=Np(ωTs)ejθp(ωTs)，其中 Np(ωTs)，θp(ωTs)，分别为应离散对象的幅频特性和相频特性，则(6)式可表示为

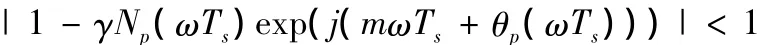
整理得:

其必要条件为

考虑模型与系统不完全匹配，引入一定的鲁棒裕度ε＞0，仿真时考虑必要条件:

2.2.2 算法实现

由上述分析可知，实际应用时，首先根据式(8)确定最佳的超前步长，随后由(7)式选取合理的学习增益γ，分两步独立设计参数，实现过程简单，这在仿真部分可具体了解。

学习参数确定后，根据(3)式所示的学习律修正控制输入。须注意的是，由(3)式知，t∈(T-Δ，T］这部分的控制输入信号，需要用t∈(T，T+Δ］时的误差信号，显然这是不可能得到的，本文利用ek(T)分别代替ek(T)，t∈(T，T+Δ］的值，由仿真可知，这对学习过程的收敛性、跟踪性能等基本没有影响。

3 活塞外圆加工预期迭代学习控制仿真

采用第二章设计所得到的控制模型进行仿真，

重写其传递函数如下:

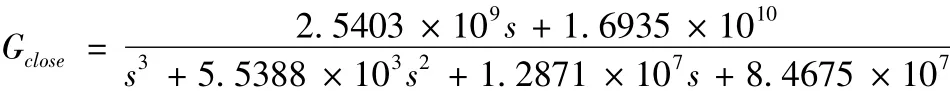
取采样周期Ts=0.00005s，利用阶跃响应不变法对其离散化得Gp(z)如式(9)所示。

期望轨迹是复杂截面数据如图4。

令ε=10°，图(5)给出了周期为Ts=0.00005s时，不同的 m值所对应的 θp(ωTs)+mωTs。可以看到，当m=0时，即对象自身的相频特性，在频率为600Hz以上时，其相位就已在-80°以下，显然不满足条件(8)式;当m=4时，如图所示，可学习频带最宽，此时频率在4000Hz以下均能满足必要条件(8)式，故最佳超前步长为m=4。

图5 Ts=0.00005s时超前步长的选择

图6、图7同时给出了Ts=0.00005s时离散A型ILC的跟踪性能，这里假设系统无噪声、无初态响应的影响，可见系统第40次输出已基本与期望轨迹重合。可以看出，系统在幅值和相位上都有了很大的改善，能够很好的跟踪期望输出。图8给出了系统输出与期望输出之间误差最大值与迭代次数的关系，可以看出，随着迭代次数的增加，误差在逐渐减少并趋向于零，当迭代40次后迭代输出与期望输出的最大误差为0.0012mm。仿真实验说明，通过预期迭代学习控制，改变控制输入量(图8)能够改变系统的输出。

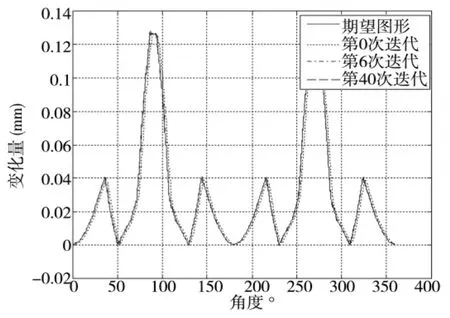
图6 离散A型ILC迭代学习控制输出效果

图7 离散A型ILC迭代学习局部放大

图8 误差最大值

图9 迭代40次后的输入数据

4 结束语

本文将预期学习控制方法应用于活塞外圆异型数控加工数据的控制，考虑到计算机的离散控制，直接在离散频域内设计学习律、分析控制性能。该方法利用线性相位超前抵消对象本身相位滞后的影响来拓宽系统的可学习频带，并采用两步设计方法得到满足条件的学习律，仿真表明它能很好地跟踪快速响应的系统。

［1］Stefan R，James F.C.Design and testing of a long-range，precision fast tool servo system for diamond turning［J］.Precision Engineering，2009(33):18-25.

［2］WU D，CHEN K，WANG X K.Tracking control and active disturbance rejection with application to noncircular machining［J］.International Journal of Machine Tools ＆ Manufacture，2007(47):2207-2217.

［3］Adam A.C，Hiram A.F，Matthew T.B，etc.Workpiece dynamic analysis and prediction during chatter of turning process［J］.Mechanical Systems and Signal Processing，2008(22):1481-1494.

［4］Wang D W，Ye Y Q.Design and experiment of anticipatory learning control:frequency domain approach［J］.IEEE/ASME Transactions on mechatronics，2004，1(11):1-6.

Piston Digital Controlled Manufacture Based on Iterative Learning Control with Anyicipation Control

FENG Zong-jie，WANG Xu-dong，ZHANG Jin-li，HUANG Hua
(The Second Artillery Petty Officer College，Qingzhou Shandong 262500，China)

Because of gain attenuation of the high speed precision servo system，large tool tracking error will be produced and machining accuracy required will be lost during high speed and fine turning of noncircular components.Anyicipation learning control method based on iterative learning control is design for Piston Digital Controlled Manufacture.the convergence condition in frequency domain is derived.The simulation results are presented to demonstrate the effectiveness of the proposed iterative learning control on Piston Digital Controlled Manufacture.

piston;iterative learning control;anyicipation learning control;convergence

TH16;TG65

A

1001-2265(2012)02-0077-04

2011-06-01

冯宗杰(1982—)，男，山东潍坊人，第二炮兵士官学校助教，研究方向为机械制造，(E-mail)fengzongjie@163.com。

(编辑 李秀敏)