并联式髋关节摩擦特性试验机驱动机构运动学研究*

顾 伟，程 刚，徐 鹏，于敬利

(中国矿业大学机电工程学院，江苏徐州 221116)

并联式髋关节摩擦特性试验机驱动机构运动学研究*

顾 伟，程 刚，徐 鹏，于敬利

(中国矿业大学机电工程学院，江苏徐州 221116)

为了克服现有髋关节试验机在复杂运动轨迹模拟和变载荷动力加载等方面存在的不足，试制了一台以3SPS+1PS并联机构为核心驱动模块的髋关节试验机。基于Rodrigues参数，对该髋关节试验机的驱动机构进行了运动学建模和求解。根据ISO14242-1:2002(E)标准的相关规定，对该机构逆运动学模型进行了数值仿真，得到模拟髋关节运动所需的主动件运动学参数变化规律，确定了该髋关节试验机的运动方案，并验证了驱动件选型的合理性。通过耗时计算，测得Rodrigues参数法求解试验机逆运动学的运算时间，满足控制实时性的需要。

髋关节试验机;3SPS+1PS并联机构;Rodrigues参数;运动学分析;数值仿真

0 引言

人工髋关节是人体重要的替代器官，它是模拟天然髋关节而制成的植入性假体，以代替病变或损坏的关节并恢复其功能。评价人工髋关节材料的摩擦磨损特性需要进行摩擦学试验。目前国内外髋关节试验机的驱动机构大多采用串联机构。串联驱动机构的各自由度串接相连、传动链长、累积误差较大导致其驱动精度较低。而且串联机构的位置逆解复杂，而试验机要求在线实时计算位置逆解，这势必使串联驱动机构在复杂运动轨迹模拟方面的运用受到限制。目前国内外的串联式髋关节试验机大多通过简化试验运动曲线的方法来缩短传动链的长度和降低实时控制的难度，例如忽略髋关节的外展/内收(AA)运动。这种简化使得模拟运动与人体髋关节的实际运动曲线相差较大，对试验结果有不良影响。此外串联式髋关节试验机的末端自由度普遍采用悬臂结构，这使得其承载能力降低，在变载荷动力加载时会出现机构振动和变形等问题。

相对于串联机构，并联机构精度高、工作速度快、刚度大、承载能力强，此外结构简单惯性小［1］。经历半个多世纪的发展，并联机构已经在很多地方得到了成熟的运用，其中重要的一项运用就是运动模拟器，如基于Stewart平台的并联运动模拟器［2］。本文以3SPS+1PS并联机构为核心驱动模块搭建了一台髋关节摩擦磨损试验机样机。以3SPS+1PS并联机构为研究对象，分析了该髋关节试验机驱动机构的运动学特性，通过数值仿真确定了该试验机的运动方案，验证了该试验机驱动件选型的合理性。

1 3SPS+1PS髋关节试验机

根据ISO14242-1:2002(E)标准的相关规定，人工髋关节假体在进行摩擦学试验时，所采用的试验机应至少具有三个转动自由度来模拟实际人体髋关节的屈曲/背伸(FE)、外展/内收(AA)和内旋/外旋(IER)运动。试验机的运动频率应为1Hz±0.1Hz。完成一次实验，试验机至少需要持续运转5×106个周期。试验加载力为3kN±90N，按一定的规律以1Hz频率变化。ISO14242-1:2002(E)标准推荐的试验机具体参数要求如表1所示。

表1 髋关节试验机标准推荐参数

参照表1的相关规定，本文提出一种以空间结构对称的3SPS+1PS并联机构为核心驱动模块的并联式髋关节试验机，其样机如图1所示。该试验机由定动两平台构成，两平台之间由3根SPS形式的主动支链和一根PS形式的中心支柱连接。绝对坐标系{B}固定在定平台上，原点为O点。其Y轴通过A2点，Z轴垂直于定平台平面B，方向指向动平台m，X轴根据右手定则确定。相对坐标系{m}固定在动平台上，原点位于o点。其y轴通过a2点，z轴垂直于动平台平面m，指向动平台 m外侧，x、y、z三轴的方向遵循右手定则。定、动平台上球铰链围绕平台中心点均布，安装半径分别为E和e。中心支柱固定于定平台上，与动平台接合处采用推力关节轴承连接。试验加载依靠电液伺服系统控制液压缸进行变载荷动力加载。

图1 3SPS+PS并联髋关节试验机样机

2 髋关节试验机运动学分析

由于髋关节试验机控制实时性的需要，在此采用Rodrigues参数对该试验机的空间姿态进行描述，其对应的姿态旋转矩阵用Do表示［3］。

2.1 位姿逆/正解

根据建立的参考坐标系，点Ai(i=1，2，3)、ai(i=1，2，3)以及原点o的表达式如(1)所示，其中上标B表示绝对坐标，上标m表示相对坐标:

式中，e是点ai到动平台坐标系原点o的距离，E是Ai到定平台坐标原点 O 的距离。(xl，xm，xn，yl，ym，yn，zl，zm，zn)是动平台 m 在{B}中的9个方位参数，构成描述动平台m位姿变换的旋转矩阵Do。

由空间两点之间的距离公式可得支链ri(i=1，2，3)的长度表达式如式(2)所示:

各支链向量ri的单位矢量记为δi:

当给定机构运动的三个罗德里格参数Φi(i=1，2，3)和 Zo的值时，机构的输入参数(ri，δi，i=1，2，3)可以通过式(2)和(3)求得。

2.2 速度逆/正解

设V是动平台的广义速度，v和ω分别为动平台m在o点的线速度和角速度，vi为动平台m在ai点处的速度，vr为支链的输入速度，其表达式如下所示:

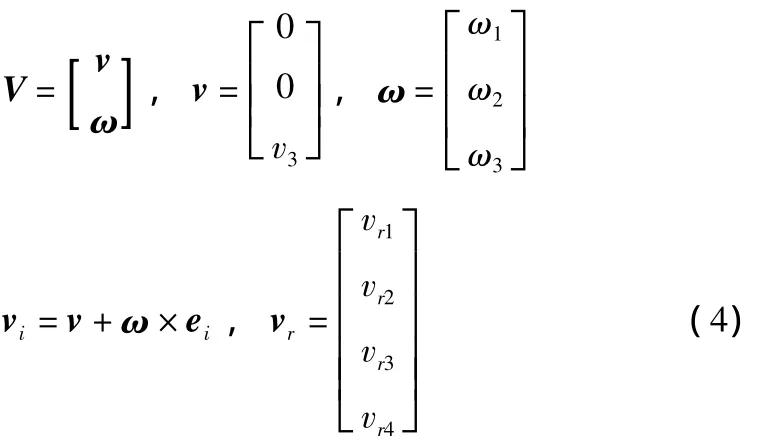
基于机构的几何特性，根据速度合成原理，由式(4)可得到沿各支链ri(i=1，2，3，4)的线速度vri(i=1，2，3，4)，其表达式如式(5)所示:

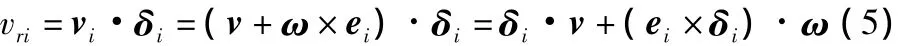
联立方程(4)和(5)可以得到输入与输出速度的关系表达式为:

其中J为速度雅各比矩阵。

2.3 加速度逆/正解分析

设A为动平台m在o点的广义加速度，a和ε分别为动平台在o点的线加速度和角加速度，ar为沿支链的输入加速度，其表达式如下所示:

文献［4］给出了沿支链方向的线加速度的标量表达式，(i=1，2，3，4):

函数S表示对向量进行斜对角化［5］。

3 运动学数值仿真

根据ISO14242-1:2002(E)标准的相关规定，选用1Hz的运动频率，对该髋关节试验机运动学模型进行数值仿真［6］。图2a为 ISO14242-1:2002(E)标准推荐的人体髋关节运动角度变化规律对应的Rodrigues参数变化规律［3］。与现有的串联式髋关节试验机普遍采用的两自由度试验运动规律曲线(如图2b所示)相比，本文提出的并联式髋关节试验机严格按照ISO14242-1:2002(E)推荐的三自由度运动规律进行运动模拟，这将使得髋关节材料的摩擦学试验结果更具有说服力。

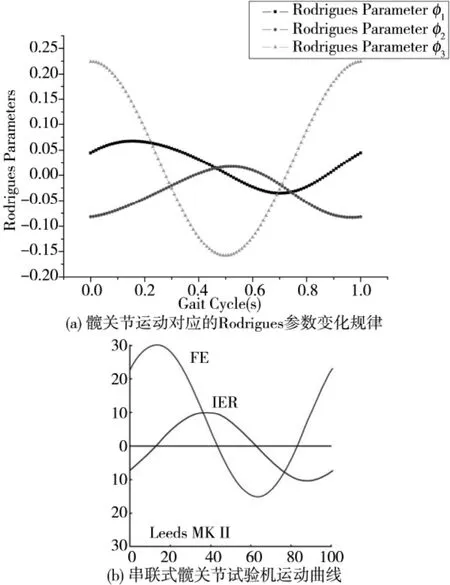
图2 髋关节试验机运动规律曲线

由于3SPS+1PS并联髋关节试验机围绕Z轴的转动范围最大，将 Z轴确定为髋关节屈曲/背伸(FE)角的旋转轴线，X和 Y轴分别为外展/内收(AA)角和内旋/外旋(IER)角的旋转轴线。试验机的结构参数和所采用的直线致动器的性能参数如表2所示。

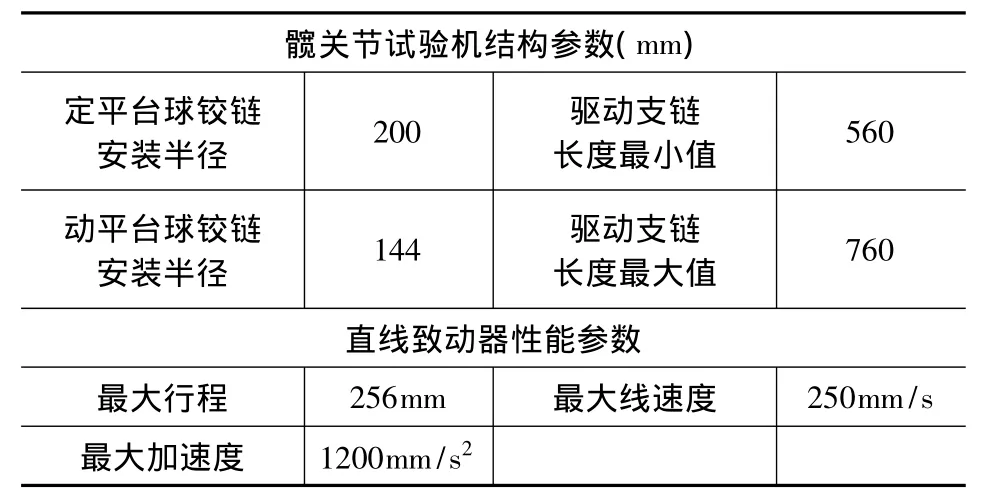
表2 3SPS+1PS并联机构的结构参数

根据式(2)可得到机构驱动件的长度变化曲线如图3所示。由图3可以看出，三根支链的伸缩量大体相同，且均在所设计的机构结构参数范围内。支链驱动杆长度变化曲线和支链长度分量变化曲线均近似于简谐曲线，过渡平滑，便于驱动杆的控制。

由式(5)和(8)可求得对应于图2中动平台m运动规律的支链驱动速度变化规律如图4a所示，对应的支链加速度变化规律如图4b所示。从图4可以看出，三个驱动支链的速度和加速度变化范围都没有超出直线致动器允许的范围。速度和加速度变化曲线过渡平滑，不存在突变点，试验机在运动过程中不存在刚性冲击，这对于机构的动态性能是有利的。

图3 驱动杆长长度变化图

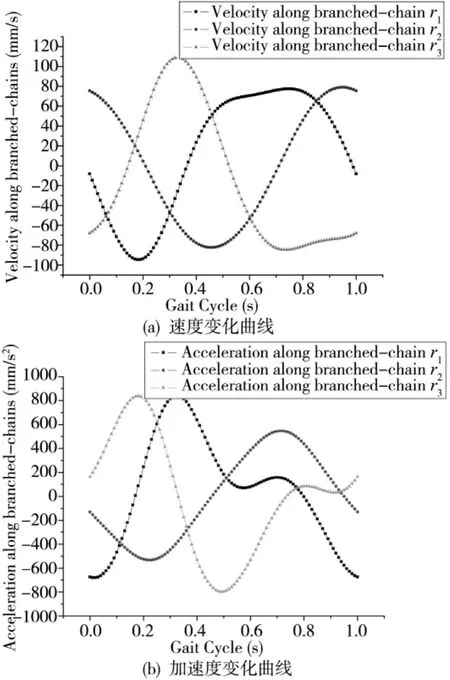
图4 主动支链的速度和加速度变化曲线

根据上述分析，将机构参考坐标系Z轴确定为屈曲/背伸(FE)角的旋转轴，满足髋关节运动模拟的要求。进一步研究表明，如果将X或Y轴线作为屈曲/背伸(FE)角的旋转轴时，主动件需要提供的运动速度、加速度都扩大了将近一倍，这样对直线制动器的性能提出了更高的要求，机构运行时由于驱动件的加速度太大而出现震动等现象，甚至会导致驱动件的损坏。故本文采用的模拟运动方案是可行的。通过对Rodrigues参数求解逆运动学模型的计算时间进行记录，测得整个逆运动学单周期平均计算耗时0.03282s，而试验机的运动频率为1Hz，故采用 Rodrigues参数描述试验机的动平台的空间位姿满足机构控制实时性的需要。

4 结束语

针对现有髋关节试验机存在的不足，搭建了一台以3SPS+1PS并联机构为核心驱动模块的髋关节试验机。建立参考坐标系，基于Rodrigues参数对该3SPS+1PS并联髋关节试验机进行了运动学建模，采用解析法对该运动学模型进行求解，得到了位置、速度和加速度表达式。根据ISO14242-1:2002(E)推荐的人体正常行走时髋关节角度变化近似规律对逆运动学模型进行了数值仿真，验证了驱动器选型的正确性，最终确定了试验机的运动方案。通过耗时计算，测得Rodrigues参数法求解试验机逆运动学的平均运算时间为0.03838s，满足控制实时性的需要。上述运动学分析为该髋关节试验机的结构优化和控制系统的构建提供了分析基础。

［1］Olazagoitia JL，Wyatt S.New PKM Tricept T9000 and its application to flexible manufacturing at aerospace industry.SAE International，Paper No.07ATC-94，2007.

［2］Chun-TaChen，Jyh-Chyang Renn，Zong-Yuan Yan.Experimental identification of inertial and friction parameters for electro-hydraulic motion simulators［J］.Mechatronics，2011(21)1-10.

［3］周江华，苗育红，王明海.姿态运动的Rodrigues参数描述［J］. 宇航学报，2004，25(5):514-519.

［4］Y.Lu，Y.Shi，B.Hu.Kinematics analysis of two novel 3UPUI and 3UPUII PKMs［J］.Robotics and Autonomous Systems，2008，56(4):296-305.

［5］Craig J.(2005).Introduction to robotics:mechanics and control.3rd ed..New York:Prentice Hall/Pearson.

［6］ISO 14242-1:2002(E).Implants for surgery-Wear of total hip-joint prostheses-Part 1:Loading and displacement parameters for wear-testing machines and corresponding environmental conditions for test.

Kinematics Study of a Driving Mechanism of a Parallel Hip Joint Simulator

GU Wei，CHENG Gang，XU Peng，YU Jing-li
(College of Mechanical＆ Electrical Engineering，China University of Mining＆ Technology，Xuzhou Jiangsu 221116，China)

In order to overcome defects in complex motion simulation and variable dynamic loading of hip joint simulators available in literature，a parallel hip joint simulator with a 3SPS+1PS parallel manipulator as core module is proposed.Its kinematic model was established and then solved based on Rodrigues parameters.According to ISO14242-1:2002(E)standard，a numerical simulation of the inverse kinematics was conducted.Then，variation laws of kinematic parameters of the driving legs were obtained.Meanwhile，motion scheme of the simulator was determined and selection of actuators was validated.Finally，the time consumption of the inverse kinematics calculation based on Rodrigues parameters was recorded which can meet the real-time demand.

hip joint simulator;3SPS+1PS parallel manipulator;Rodrigues parameters;kinematic analysis;numerical simulation

TH122;TP273

A

1001-2265(2012)02-0016-04

2011-09-14;

2011-10-21

国家自然科学基金(50905180、60808017、51005234)

顾伟(1988—)，男，江苏泰州人，中国矿业大学机电工程学院硕士研究生，研究方向为机构学等，(Email)koowei_cumt@yahoo.com.cn。

(编辑 李秀敏)