基于有限元分析的复杂结构弹性振动传递函数建模

武新峰，雷勇军，李家文

(国防科学技术大学 航天与材料工程学院，长沙 410073)

随着航天技术的不断发展和进步，航天器结构(如大型捆绑火箭、高超声速飞行器、大型空间组合体和天基动能武器等)日趋复杂化和功能化，其外形特征、内部结构及载荷边界都发生了较大的变化，产生了许多新的力学问题。航天器在运行过程中受到各种扰动(如发动机频繁开关机产生的冲击、碰撞、温度冲击等)的作用会发生弹性振动，如果这种弹性振动不能迅速衰减或者发生放大，不仅会对控制系统产生重要影响，而且可能造成结构的破坏。因此在结构设计和控制系统设计过程中，都必须考虑弹性振动的影响，才能够准确建立弹性振动的力学模型。

结构的弹性振动需要采用三维偏微分方程来描述，板壳结构的弹性振动可以简化为二维偏微分方程的初边值问题，而梁和杆的弹性振动则可以进一步简化为常微分方程的初边值问题［1］。工程实践中，采用两端自由的空间一维梁模型来建立串联火箭和大细长比导弹的弹性振动方程［2］，但该方法应用于复杂航天器的难度较大，原因在于:① 多数航天器(如卫星、天基动能武器等)结构长细比较小，不能采用二维或一维的简化模型，而建立三维偏微分方程的难度大;② 航天器内部结构错综复杂，振动传递特性难以准确模拟;③ 航天器结构中广泛采用新型材料和特殊结构，而这些材料和结构的力学特性及边界条件难以准确模拟［3］。

另外，可以采用实验法进行弹性振动建模，即将系统看作一个“黑箱”，根据输入输出数据辨识出系统的力学模型。该方法由实验和参数辨识两部分组成，辨识算法比较成熟［4－5］，在工程领域中实验法得到广泛应用［6－8］。但实验法也存在一些不足之处，主要体现在:① 航天器的载荷边界条件无法准确模拟，尤其是失重、在轨运行、在轨机动等空间环境;② 输出信号采集过程中不可避免地会受到噪声等随机信号的影响，给辨识精度造成较大影响;③ 航天器实验耗资较大，周期较长，很难通过多次实验来提高弹性振动模型的精度。

为了降低弹性振动建模的难度，综合分析以上两种建模方法的优缺点，提出了一种基于有限元分析的弹性振动传递函数建模方法。首先采用有限元软件将航天器结构进行有限元离散建模，从而降低结构的自由度数目，降低建模难度;然后基于有限元模型模拟航天器的各种实验工况，进行线性动力学分析或非线性动力学分析，得到响应数据;最后采用参数辨识算法，建立能够准确反映弹性振动的传递函数模型。本文根据参数辨识类型的不同，从时域和频域两个方面进行弹性振动传递函数建模。首先给出了基于有限元分析弹性振动建模的流程;然后通过悬臂梁、某运载火箭和某弹体局部结构的算例验证了本文方法的可行性和有效性，为工程应用提供参考。

1 弹性振动传递函数建模

在弹性振动众多的描述方法当中，传递函数模型能够直接反映激励和响应之间的关系，建模简单、应用方便，因此作为本文的首选。传递函数是描述系统动态特性的一种数学表达式，只取决于系统的结构和参数，一般为复变量的有理真分式函数，其分子和分母多项式的系数均为实数，都是由系统的物理参数决定的。

一个初始条件为零的多自由度结构系统的运动微分方程为:

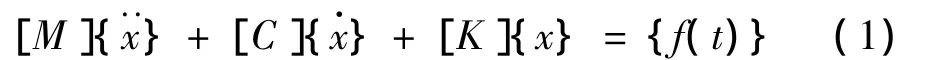
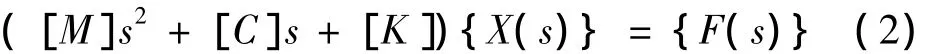
式中{F(s)}和{X(s)}分别为{f(t)}和{x}的Laplace变换。由式(2)得:

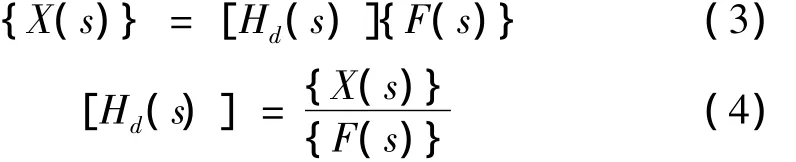
式中Hd(s)为结构的位移传递函数矩阵。下文不区分传递函数类型(位移、速度或加速度)，统一用H(s)表示。将传递函数写成有理真分式的形式为:

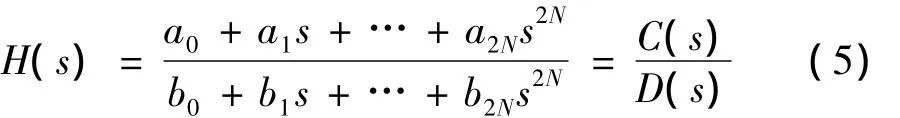
式中:N 为模态阶数，ak和 bk(k=0，1，2，…，2N)为待定系数。

对式(5)进行参数辨识确定各个系数，能够得到传递函数模型。本文根据参数辨识的3个基本要素(即模型、数据和准则)设计了基于有限元分析的弹性振动建模流程，如图1所示。整体建模分为两个模块:有限元分析模块和参数辨识模块。有限元分析模块主要作用是建立结构的有限元模型，模拟各种动力学环境，通过各种动力学分析得到参数辨识所需的数据。参数辨识模块需要根据数据类型，选择辨识的数学模型和准则进行参数辨识。有限元分析得到的数据可以为时域响应，也可以为频域响应，因此参数辨识方法也要相应地选择时域辨识法或频域辨识法。需要说明的是:有限元模型的精度需要采用模态实验结果进行校核，通过修改模型来提高有限元模型的仿真精度。而在传递函数模型的正确性验证过程中，同样需要实验结果进行验证，但是工程中往往很难得到这种实验数据，因此这里采用有限元仿真结果进行验证。当然，这样处理的前提是有限元模型足够准确。下面分别给出两种方法的实施方案。

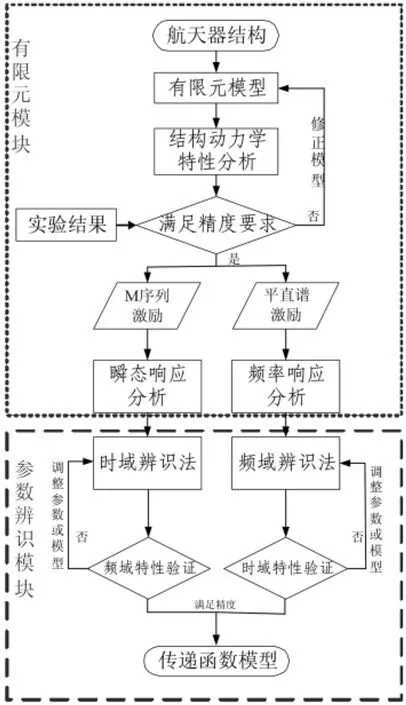
图1 弹性振动建模流程Fig.1 Elastic vibration modeling flow chart

1.1 时域辨识建模法

(1)有限元模型建立及修正

有限元模型是本文方法的基础，使用MSC.PATRAN建立有限元模型后，通过结构动力学特性分析得到固有频率和振型，与设计值或试验结果对比后修正有限元模型。

(2)时域数据准备

时域数据由MSC.NASTRAN的瞬态响应分析得到，内容包括:激励的施加、边界条件的模拟、瞬态响应分析类型的选取、响应输出位置和数据类型的选取等。激励施加主要以实际激励为主，但在实际激励未知的情况下，可以选取PRBS信号［9］(伪随机二进制序列)。这是因为PRBS信号具有近似白噪声的性质，能够保证良好的辨识精度。瞬态响应分析包括直接积分法和模态叠加法，为了便于控制辨识的频段，选用模态叠加法。

(3)模型参数辨识

时域参数辨识法是在时间域内识别结构模态参数的方法，所采用的原始数据通常是结构振动响应，包括结构的自由振动响应、冲击响应和强迫振动响应。主要有STD法、最小二乘复指数法、ARMA时序法等。其中ARMA模型的表达式为:

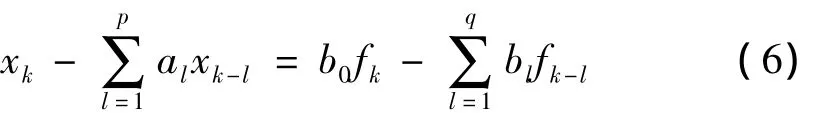
其中，fk=f(kΔt)，(k=0，1，2，…)是激励的离散值，xk=x(kΔt)(Δt为采样时间间隔)是响应的离散值，al(l=1，2，…，p)、bl(l=1，2，…，q)是待辨识参数，p、q为ARMA模型的阶次，且p≥q。对式(6)进行Z变换就可以得到与传递函数等价的形式，即:

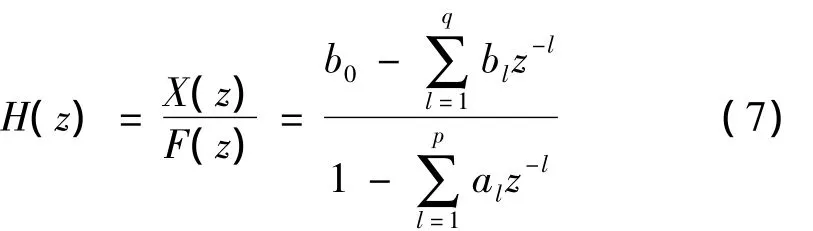
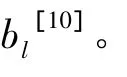
(4)模型验证

模型验证采用“时域建模频域验证”的方法，即先求得传递函数的频域特性(幅值与相位角)，然后与MSC.NASTRAN分析得到的频响函数曲线进行对比，如果频域特性一致，则认为传递函数模型满足精度要求。

1.2 频域辨识建模法

(1)有限元模型建立及修正

(2)频域数据准备

频域数据由MSC.NASTRAN的频率响应分析得到，计算时以幅值为1的平直谱曲线为激励，可以直接得到结构的频响函数曲线。

(3)模型参数辨识

频域参数辨识法是指在频域内对结构模态参数进行辨识的方法。主要利用线性参数或非线性参数最小二乘法进行曲线拟合的多种频域参数辨识法，例如导纳圆拟合法、频域最小二乘法、有理分式多项式法(Levy法)、正交多项式法等。其中Levy法的数学模型为频响函数的有理式形式，而频响函数与传递函数等价，即将式(5)中的s换为jω，令b0=b2N=1可得到频响函数:

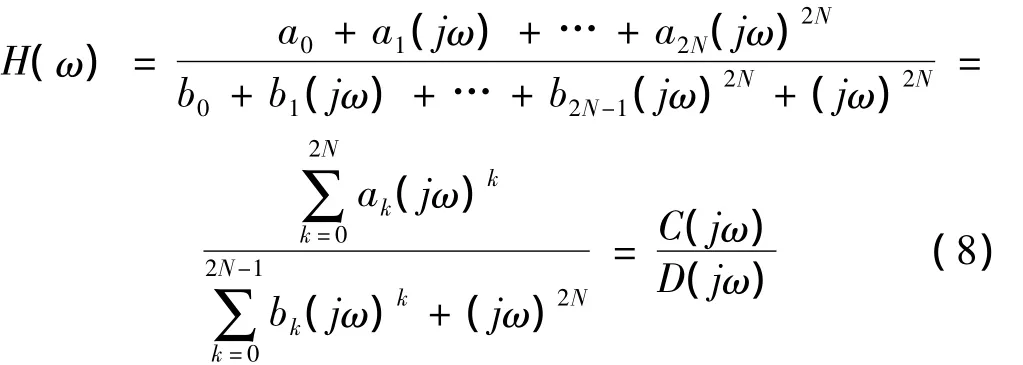
采用最小二乘法即可得到式(8)待定系数ak和bk［10］。

(4)模型验证

模型验证采用“频域建模时域验证”的方法，对传递函数模型和有限元模型施加同一个时域激励，对比时域响应的结果，如果结果误差较小，则认为传递函数模型准确。

当然，时域和频域参数辨识法还有许多，而且随着诸多新技术的引入辨识精度越来越高。本文之所以选择以上两种方法，只是因为其数学模型与传递函数等价。在实际操作中，可以根据需要选择参数辨识算法。

2 算例分析

为了验证本文方法的可行性、有效性，下面给出三个算例进行计算和分析:

2.1 算例1:悬臂梁

悬臂梁结构简单，有限元分析结果精度高，振型容易判别，因此选取悬臂梁算例来验证基于有限元分析弹性振动建模方法的可行性和有效性。如图2所示，杆件长1 m，截面直径0.005 m，材料为1Cr18Ni9Ti。杆件划分为20个Beam单元，梁左端点固支约束，距固支点0.05 m处施加加速度激励，右端点加速度响应作为输出。

图2 悬臂梁有限元模型Fig.2 Finite element model of cantilever beam

首先采用SOL103进行结构动力学特性分析，得到前三阶横向弯曲固有频率值和模态振型，分别是3.54 Hz，22.11 Hz和 61.74 Hz。

然后分别以PRBS信号曲线和平直谱曲线(频率范围是0～80 Hz)的曲线为加速度激励，采用SOL112和SOL111进行瞬态响应分析和频率响应分析，得到时域响应曲线和频响函数曲线后，依次采用ARMA模型和Levy法进行弹性振动建模。两种方法得到的加速度传递函数为:

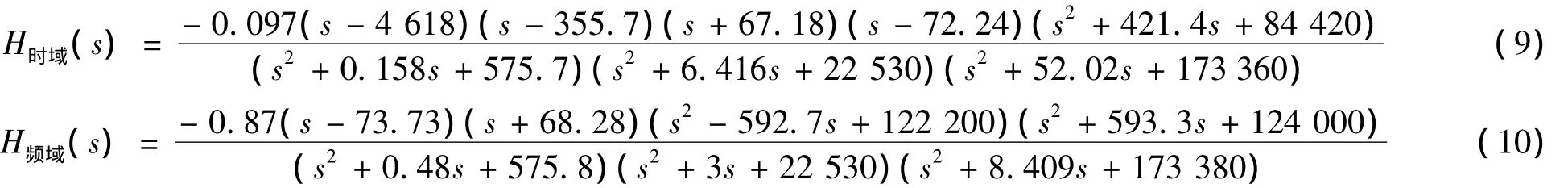
采用时域参数辨识法进行建模时，传递函数模型的阶次较高，式(9)是模型降阶处理后的结果。对比两个传递函数的分母不难看出，前三阶横向振型的固有频率值辨识误差较小。

最后按照“时域建模频域验证，频域建模时域验证”的方法，进行传递函数模型验证。图3给出了以PRBS信号为加速度激励的时域响应曲线，对比了传递函数模型式(9)、式(10)和有限元模型的时域响应特性。从时域响应曲线来看，时域辨识模型的精度要优于频域辨识模型。图4和图5分别给出了以上三个模型的幅频特性和相频特性曲线，表明三个模型的固有频率值一致，但时域辨识模型(式9)幅频曲线峰值的大小与有限元模型相比存在误差，因此从频域特性来看，频域辨识模型的精度要优于时域辨识模型。

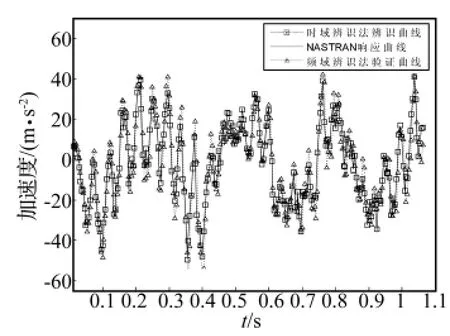
图3 悬臂梁时域响应曲线Fig.3 Transient response of cantilever beam

从以上分析可以得出，时域辨识建模能够得到很好的时域辨识结果，但频域特性会有较小误差;而频域辨识建模刚好相反，频域特性的精度更高，时域特性有较小的误差。因此，在建模过程中，根据需要选择建模方法。

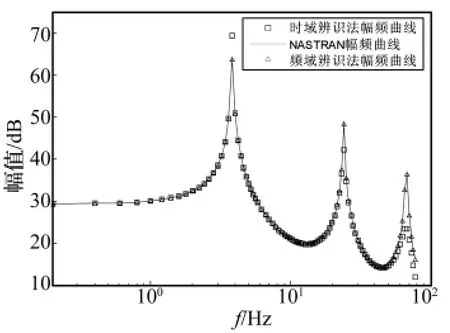
图4 悬臂梁幅频曲线Fig.4 Magnitude response of cantilever beam

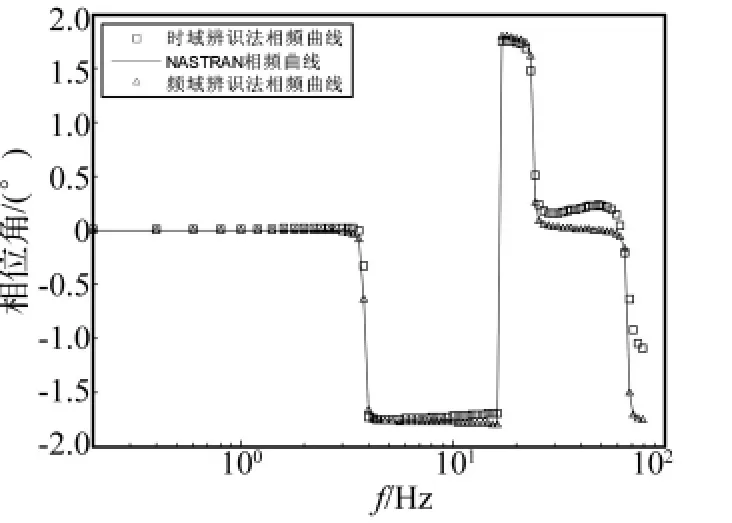
图5 悬臂梁相频曲线Fig.5 Phase angle response of cantilever beam

图6 运载火箭梁模型及横向弯曲振型Fig.6 Finite element model and bending mode shapes of rocket

2.2 算例2:运载火箭

简化为梁模型(如串联运载火箭、导弹等)的弹性振动建模方法已经很成熟，但是这种方法的简化程度较大。随着火箭的运载能力越来越大，火箭的直径逐渐增大，长细比减小，并且增加了捆绑助推火箭，故而不能简单地采用梁模型进行弹性振动建模。为了更准确地考虑火箭在不同秒状态下弹性振动的影响，基于线性系统假设，可以采用本文的方法建立弹性振动传递函数，然后将其叠加到控制系统当中。本算例建立了某捆绑火箭的梁模型，采用频域辨识建模法得到了火箭在推力激励作用下，振型节点位置的角速度响应传递函数，从而验证本文方法在火箭、导弹等复杂结构的应用价值。

如图6给出了某运载火箭的简化有限元模型(火箭轴向为X向)。其中，推进剂用质量点进行模拟。运载火箭在飞行过程中，结构动力学特性随着推进剂的消耗而时刻变化，在分析过程中将其离散为多个秒状态。本文仿真运载火箭发射升空后的某个秒状态，边界条件为自由－自由。结构动力学特性分析表明，火箭在低频段的模态振型非常密集。图6同时给出了火箭前三阶横向弯曲振型图，振型图中标出了振型节点N1、N2 和 N3。

为了得到更准确的频域特性，这里采用频域参数辨识法进行弹性振动建模，以2台芯级发动机和4台助推发动机的推力作为输入信号，以节点N2的Z向角速度作为输出信号。建立角速度传递函数并降级处理后为:

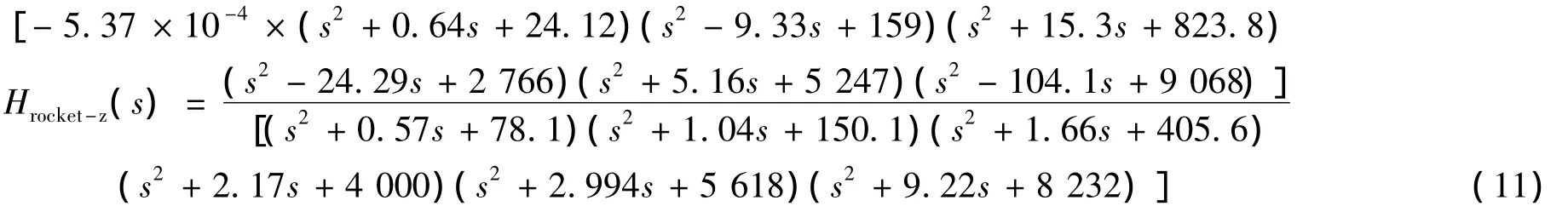
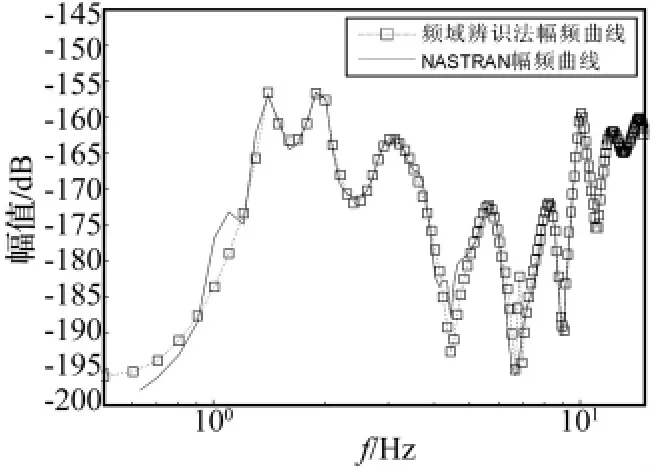
图7 Z向角速度幅频曲线Fig.7 Magnitude response of Z － direction angular velocity

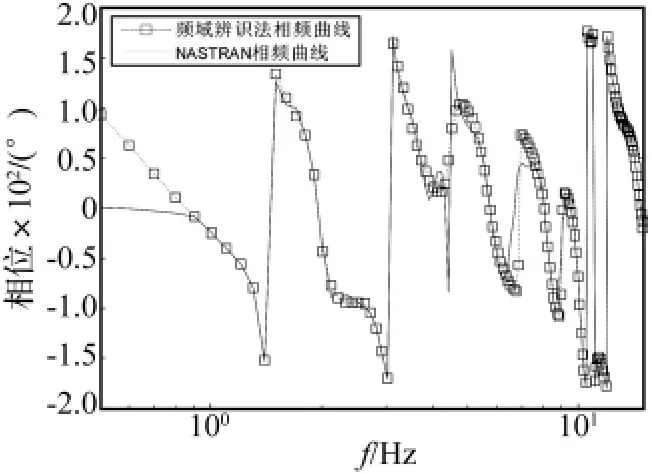
图8 Z向角速度相频曲线Fig.8 Phase angle response of Z-direction angular velocity

从式(11)的分母可以看出，在15 Hz频段内对N2位置的Z向角速度产生影响的主要模态振型有6个。该传递函数模型阶次较高，按传统方法建模难度较大，而本文方法大大降低了建模难度，建模过程更加快捷、简单。图7和图8给出了节点N2 Z向角速度响应的幅频和相频辨识曲线，与有限元分析对比说明传递函数辨识精度较高。在实际应用过程中，同样可以得到运载火箭不同秒状态、任意位置、任意方向的加速度、角位移和角速度等响应的传递函数，提高了弹性振动模型的准确性。

2.3 算例3:弹体局部结构

对于不能简化为梁模型的复杂弹性结构(如卫星、动能武器、弹体的某一舱段等)，采用偏微分方程很难准确描述其弹性振动，在这种情况下，只需建立该结构的有限元模型，然后通过本文方法就可以很好地解决局部弹性振动的建模难点。如图9给出了一个弹体局部结构(某一舱段)的惯导元件安装平台有限元模型，主要由梁和板壳单元构成空间三维结构。下端安装有发动机，上端惯组安装位置输出加速度响应。采用频域参数辨识法建立弹性振动传递函数模型为:

图9 弹体局部结构有限元模型Fig.9 Finite element model of missile’s local structures

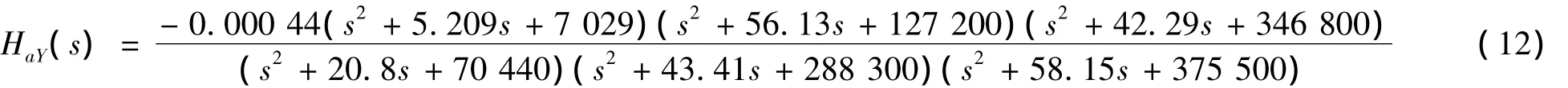
图10和图11给出了Y向加速度的幅频和相频辨识曲线，可以看出，频率特性辨识的精度较高。

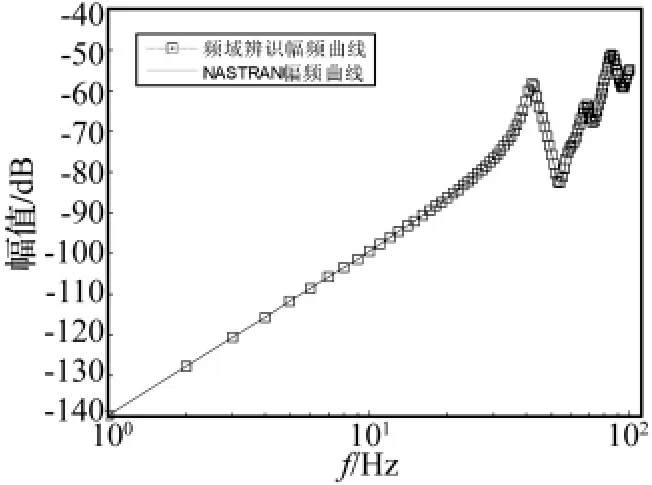
图10 Y向加速度幅频曲线Fig.10 Magnitude response of Y-direction acceleration

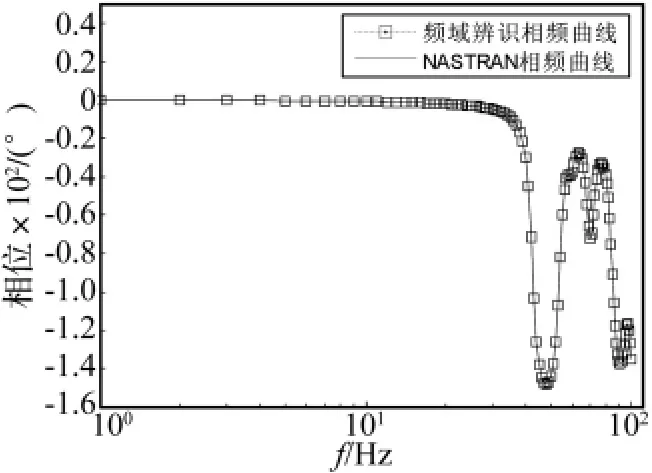
图11 Y向加速度相频曲线Fig.11 Phase angle response of Y-direction acceleration

在实际应用中，控制系统要求传递函数的阶数不能过高，可以通过以下两种途径来实现:① 数据预处理:对辨识数据进行滤波，去掉不关心的响应峰值，同时缩小频率辨识范围;② 模型降阶:通过采用降阶算法，对传递函数进行降阶。滤波和降阶的方法比较多，这里就不作介绍。

3 结论

航天及其它工业领域中的结构越来越复杂，控制精度要求却越来越高，因此以前建模中经常忽略或简化的整体或局部弹性振动因素就必须考虑在内。本文提出了一种基于有限元分析的弹性振动传递函数建模方法，以传递函数为媒介，采用参数辨识方法将有限元分析结果转换为控制系统仿真软件(如Simulink)可以应用的形式。通过对建模方法和算例验证得出以下主要结论:

(1)提出了基于有限元分析的弹性振动建模流程，分别从时域和频域讨论了传递函数建模的方法;

(2)分别建立了悬臂梁、某运载火箭和某弹体局部结构的弹性振动传递函数模型，验证了本文方法的可行性和有效性，表明本文方法可以应用到梁模型以及更复杂的航天器结构的弹性振动建模，同时可以推广应用到复杂结构之间的载荷传递、边界模拟等过程当中。

［1］李惠斌.振动理论与工程应用［M］.北京:北京理工大学出版社，2006.

［2］徐延万.控制系统［M］.北京:中国宇航出版社，1989.

［3］Arkov Y V，Kulikov G G，Breikin V T.Dynamic model identification of gas turbines［C］.UKACC International Conference on Control'98，1998:1367 －1371.

［4］Richard J.Frequency domain structural identification［D］.Monterey:University of California，1996.

［5］Pintelon R. Parameteridentifications in the frequency domain-A survey［J］.IEEE，1994，39(11):2245－2260.

［6］Mota S D J，Botez R M.New identification method based on neural network for helicopters from flight test data ［J］.AIAA，2009，2009(5938):1－31.

［7］郑勇斌，林 丽.弹体振动传递函数测试及其数据应用［J］.现代防御技术，2009，37(4):50－54.

［8］王亚斌，刘明杰，谭惠民.弹引系统传递函数系统辨识［J］.机械工程学报，2008，44(3):200－204.

［9］方崇智，萧德云.过程辨识［M］.北京:清华大学出版社，1988.

［10］曹树谦，张文德，萧龙翔.振动结构模态分析－理论、实验与应用［M］.天津:天津大学出版社，2001.