橡胶隔振器静态力－位移关系计算方法的研究

何小静，上官文斌

(华南理工大学 机械与汽车工程学院，广州 510641)

橡胶材料作为一种高性能的超弹性材料，广泛地应用于汽车隔振器，如汽车动力总成悬置、车身悬置、排气管吊耳、底盘衬套等。橡胶材料是一种大变形的非线性超弹性材料，对其进行力－位移分析时，其本构模型的选择和本构模型常数的获取是一项重要的工作。目前可用于橡胶隔振器静态力－位移关系计算的本构模型的较多，如Mooney-Rivlin、Ogden等。不同本构模型的常数不一样，如何合理的选择本构模型和开展哪些实验以获取本构模型的常数是橡胶隔振器静态力－位移分析的重要工作。

Seibert等［1］对 Arruda-Boyce 模型、Van Der Waals模型、Yeoh模型三种本构模型进行对比研究。黄建龙等［2］利用Mooney-Rivlin模型和Yeoh模型对橡胶材料进行有限元分析，介绍两种本构模型材料常数的获取方法。王丽荣等［3］利用Mooney-Rivlin模型和Ogden模型对橡胶隔振器静态力－位移特性进行有限元分析，介绍了单元特性和网格质量对橡胶隔振器静态特性的影响。Gracia等［4］研究了一种应用于工业橡胶材料弹塑性特性分析的overlay模型，并介绍其常数拟合过程。Stefan Hartmann等［5］研究了一种获取橡胶本构模型材料常数的新方法－光学测量法，确定采用光学测量法获取材料常数的准确性。

本文选取了目前广泛应用的几种本构模型来研究橡胶隔振器力－位移关系计算结果的影响因素。为获得各本构模型的材料常数，开展了橡胶材料在不同应力－应变状态(单轴拉伸、等双轴拉伸和平面剪切)和不同最大应变下的应力－应变关系的测试。利用所测得的应力－应变关系，和不同本构模型得到的理论应力－应变关系，根据最小二乘法获得不同本构模型中的材料常数。利用获得的材料常数，对两种橡胶隔振器(橡胶悬置1，2)的静态力－位移特性进行了计算并和实测值进行了对比分析。

分析结果表明，利用同一本构模型计算隔振器的静刚度时，对悬置1，在拉压变形的方向，采用三种应力－应变状态拟合得到的本构模型常数计算得到静刚度值，比单轴拉伸应力－应变状态下的计算精度高;对只有剪切变形的方向，用平面剪切应力－应变状态拟合得到的本构模型常数计算得到的静刚度，比三种应力－应变状态下的计算精度高。对悬置2，在同一本构模型下，利用单轴拉伸、等双轴拉伸和平面剪切三种应力－应变状态拟合得到的本构模型常数计算出的静刚度值，比在两种应力－应变状态下计算出的静刚度值相对误差更小。

以橡胶悬置2为研究对象，分析了不同本构模型对橡胶隔振器静态力－位移特性计算结果的影响。结果表明，Mooney-Rivlin模型的计算精度最高，其相对误差均小于10%，其次是Arruda-Boyce模型，计算相对误差最大的是Marlow模型。

1 橡胶隔振器力－位移分析的本构模型

对橡胶隔振器进行静态特性计算时，假定橡胶材料为各向同性的超弹性材料［1］。通过对其应变能密度函数对应变不变量求导，可以得到材料的工程应力与工程应变之间的本构关系［6］。工程应力和工程应变是忽略因施加载荷的增加或者减少而引起的横截面面积的变化所得到的应力、应变［15］。

超弹性材料的应变能密度函数有多种形式，如Mooney-Rivlin 模型［2］、Van Der Waals 模型［9］、Marlow模型［9］、Ogden 模型［10］、Yeoh 模型［2］、Arruda-Boyce 模型［3］、Neo-Hookean 模型、Ploynomial模型［7］等。本文只讨论目前广泛应用的前六种本构模型，及其常数的获取。

应变能密度函数的一般表达式为［8］:

其中，I1、I2、I3分别为一阶、二阶、三阶应变不变量，它们为三个主拉伸比的函数;Ci(i=1，2，…，m)为m个表示超弹性材料剪切特性的常数，dj(j=1，2，…，n)为n个表示超弹性材料压缩特性的常数。I1、I2、I3与超弹性材料的三个主拉伸比λ1、λ2、λ3的关系为:

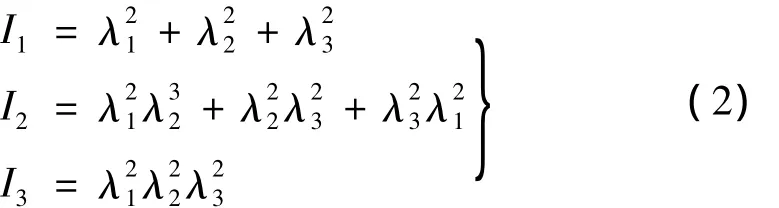
由文献［2－3］、文献［9－10］中对应的各种应变能密度函数，对三个主拉伸比 λ1、λ2、λ3分别求导数，就可以计算出材料在不同变形状态时的工程应力［8］:

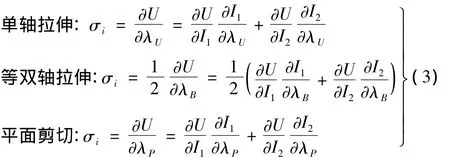
其中λU、λB和λP分别为测试得到的单轴拉伸、等双轴拉伸和平面剪切收缩率。三种不同的变形方式的应变不变量(I1，I2)与主拉伸比之间的关系，可由式(2)求得。

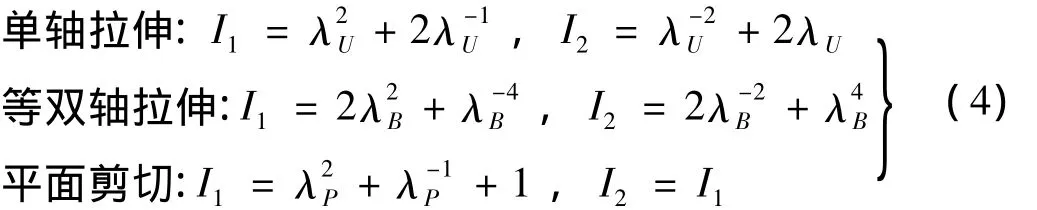
采用最小二乘法拟合实测的应力－应变和由本构模型计算得到的应力－应变，可以求得各本构模型的材料常数:

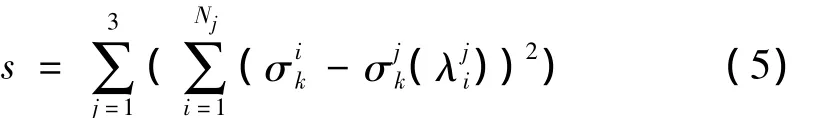
2 橡胶材料的应力－应变关系实验测试

根据上节所述的不同本构模型的材料常数获取方法，在对橡胶材料进行应力－应变测试时，对橡胶试件进行单轴拉伸、等双轴拉伸以及平面剪切实验［11］，以获得橡胶材料在不同应力－应变状态和不同最大应变下的应力－应变关系。橡胶材料的应力－应变实验是委托美国Axel Products，Inc测试的［12］。测试用的橡胶材料的邵氏硬度为50。

图2为在不同应力－应变状态和不同最大应变下，实测的工程应力－工程应变关系。在同一应力－应变状态，不同的最大工程应变时，工程应力－工程应变曲线是不重合的，在加载和卸载过程中的应力－应变曲线也是不重合的。这是由于橡胶材料存在Mullins效应［13］的作用:即在对橡胶试件进行实验过程中，在加载和卸载中应力会出现变小的现象。在进行橡胶材料的应力－应变测试时，为保证计算精度以及减小Mullins效应的影响，取循环加载(循环次数一般为5次)的最后一次应力－应变数据为实测的工程应力与工程应变的关系［14］。

图1 橡胶材料的应力－应变测试图Fig.1 The stress versus strain experimental diagram of rubber material

图2 实测工程应力－工程应变关系图Fig.2 The experimental engineering stress versus engineering strain relations3本构模型材料常数

3 本构模型材料常数

3.1 应力－应变组合

由于等双轴拉伸等效单轴压缩［1］，且本文计算的橡胶隔振器的总体变形的应变水平小于0.5，故等双轴拉伸应变的最大值仅取1。为了研究应变状态和最大应变对橡胶隔振器的力－位移计算结果的影响，选取其中不同应力－应变状态和最大应变进行组合，以得到同一本构模型在不同应力－应变状态和最大应变下的本构模型常数。不同应力－应变状态和最大应变组合如表1所示。

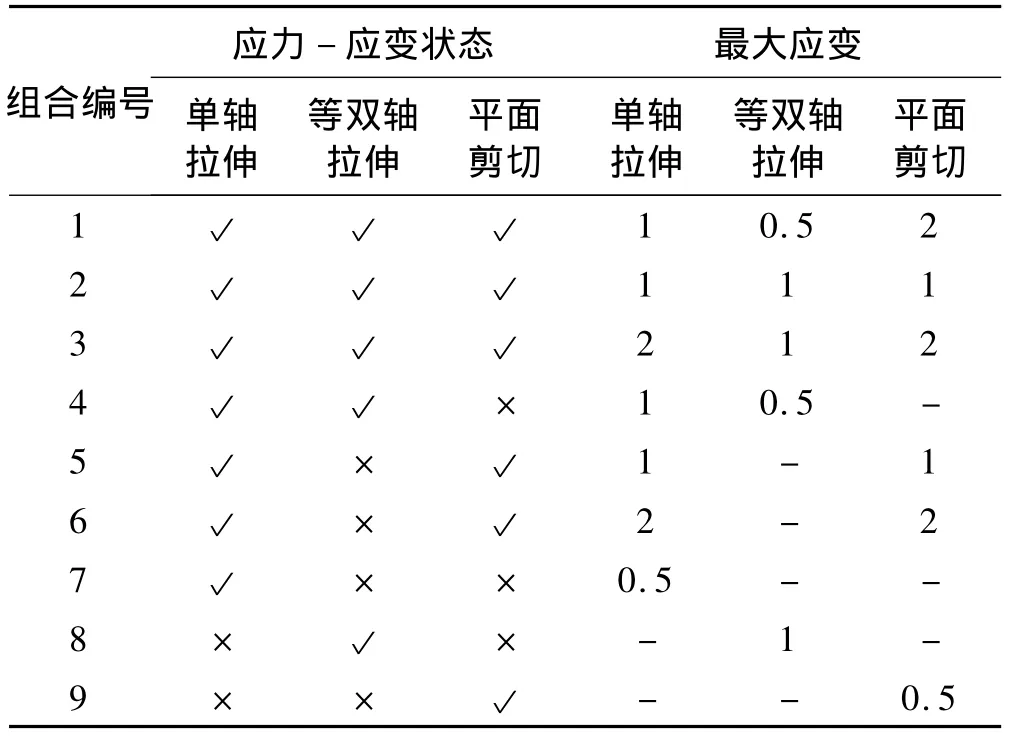
表1 应力－应变状态和最大应变组合Tab.1 Stress versus strain conditions and maximum strain combination

3.2 应力－应变拟合值和实测值的对比及材料常数

图3所示为邵氏硬度为50的橡胶材料实测以及拟合的工程应力－工程应变曲线。选取1号、3号组合计算结果进行分析。

由图3可见:

(1)在单轴拉伸应力－应变状态下，1号、3号组合时，Mooney-Rivlin模型拟合效果最好，Marlow模型拟合测试曲线趋势较好，Van Der Waals模型拟合效果相对较差，其他三种本构模型拟合材料常数效果较好。

(2)在等双轴拉伸应力－应变状态下Mooney-Rivlin模型拟合效果最好，其次是Van Der Waals模型，Ogden模型和Yeoh模型相对于Mooney-Rivlin模型来说，拟合效果相对较差，拟合效果最差的是Marlow模型，特别在3号组合时，Marlow模型拟合曲线基本偏离实测应力－应变曲线。

(3)在平面剪切应力－应变状态下，Mooney-Rivlin模型拟合误差最小，其次是Arruda-Boyce模型，拟合效果相对较差的是Marlow模型。

综合以上分析结可知，Mooney-Rivlin模型在单轴拉伸、等双轴拉伸和平面剪切三种应力－应变状态下的拟合效果最好，Arruda-Boyce模型和Van Der Waals模型次之，拟合效果最差的是Marlow模型。表2列出了在表1中的九种应力－应变状态和最大应变组合下，各本构模型的材料常数。

4 本构模型常数对橡胶隔振器力－位移关系计算结果的影响

本文选取两种不同类型的悬置做为研究对象。悬置1主要承受拉压或者剪切变形，而悬置2则同时承受拉压和剪切变形。

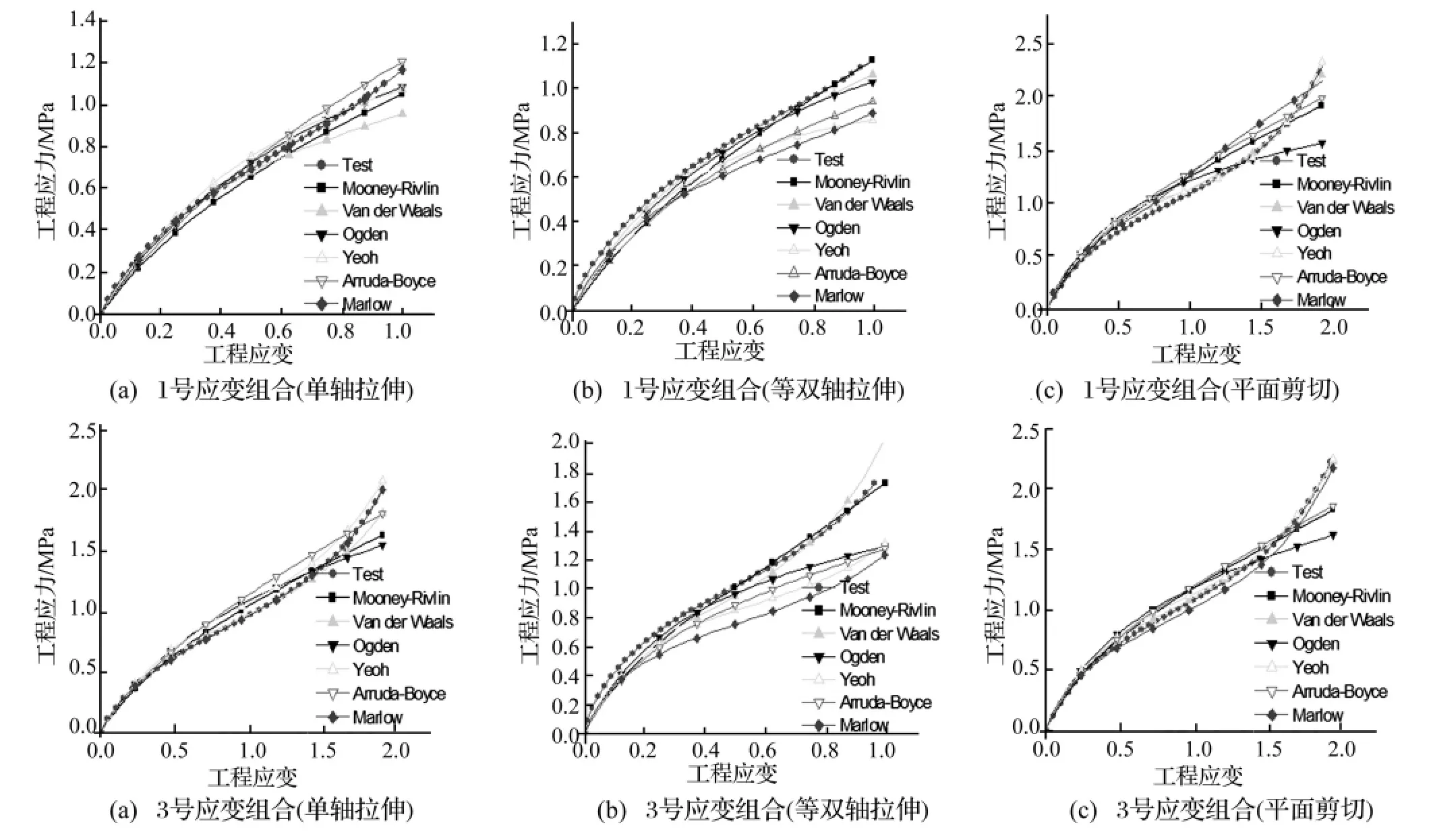
图3 1、3号组合下，实测与拟合的工程应力－工程应变曲线Fig.3 The experiment and estimated curves of engineering stress versus strain under combination 1，3

4.1 悬置1

图4所示的橡胶悬置在X向只承受拉压、Y向只承受剪切。在对此橡胶悬置进行有限元分析时，在X、Y、Z 三向均加载 5 mm的位移，计算所需的外力。

用Mooney－Rivlin本构模型，利用表1中的1号、2号、3号、4号、5号和7号、8号、9号应力－应变状态组合和不同的最大应变状态得到的本构模型材料常数，对悬置1进行三向静刚度的有限元计算。计算得到的悬置1在X、Y、Z三个方向的刚度和实测值的对比见表3～表5。

由表3可见，在悬置只承受拉压变形的X向，利用1号、2号、3号组合拟合得到的本构模型常数，计算得到的静刚度，比只在单轴拉伸应力－应变状态(7号)下计算的静刚度相对误差小。

由表4可见，在悬置只受剪切变形的Y向，利用三种应力－应变状态拟合得到的材料常数，计算得到的静刚度，比只在平面剪切应力－应变状态(9号)下计算得到的静刚度相对误差大。

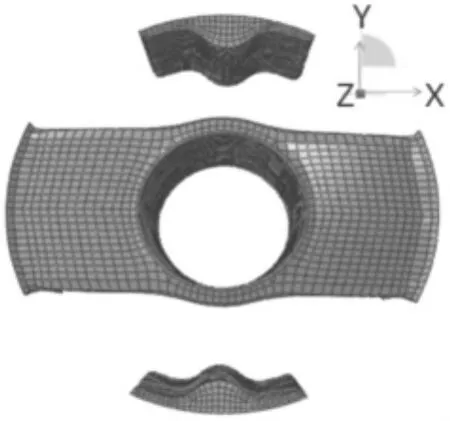
图4 悬置1有限元模型Fig.4 FEA mode of mount I

由表5可见，在同时承受压缩和剪切应力的Z向，在单轴、等双轴拉伸两种应力－应变状态下计算的静刚度相对误差最小，而在实测等双轴拉伸应力－应变状态(8号组合)下计算得到的静刚度相对误差最大。

4.2 悬置2

图5所示的悬置2橡胶主簧同时承受拉压变形和剪切变形。在进行力－位移关系计算时，X向加载力的范围从 －3 500～3 500 N;Y向加载力的范围从－500～500 N;Z向加载力的范围从 －1 000～1 000 N。

(1)利用Mooney-Rivlin本构模型，和不同实测应力－应变组合下拟合得到的本构模型材料常数，计算其三向力－位移曲线，计算结果见图6。在X向和Z向，Mooney-Rivlin模型在1号应力－应变组合下计算得到静刚度值与实测值的相对误差较小;在Y向，在3号应力－应变组合下计算的静刚度与实测值的误差较大。

(2)利用Arruda-Boyce模型、Van der Waals模型、Ogden模型和Yeoh模型，选取4组应力－应变状态组合，对悬置2进行三向静刚度计算。计算结果分别见表6、表7、表8和表9。由表6～表9可见，由三种应力－应变状态下计算的静刚度值，比用两种应力－应变状态下计算得到的静刚度值更准确。

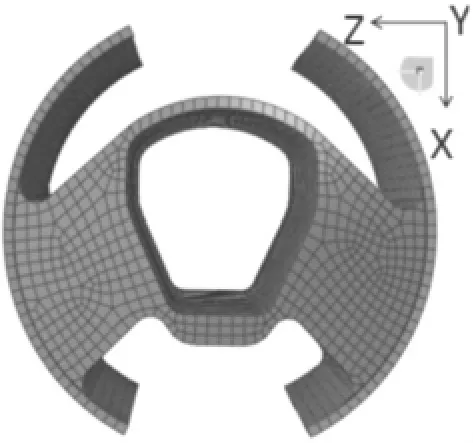
图5 悬置2有限元模型Fig.5 FEA mode of mount II

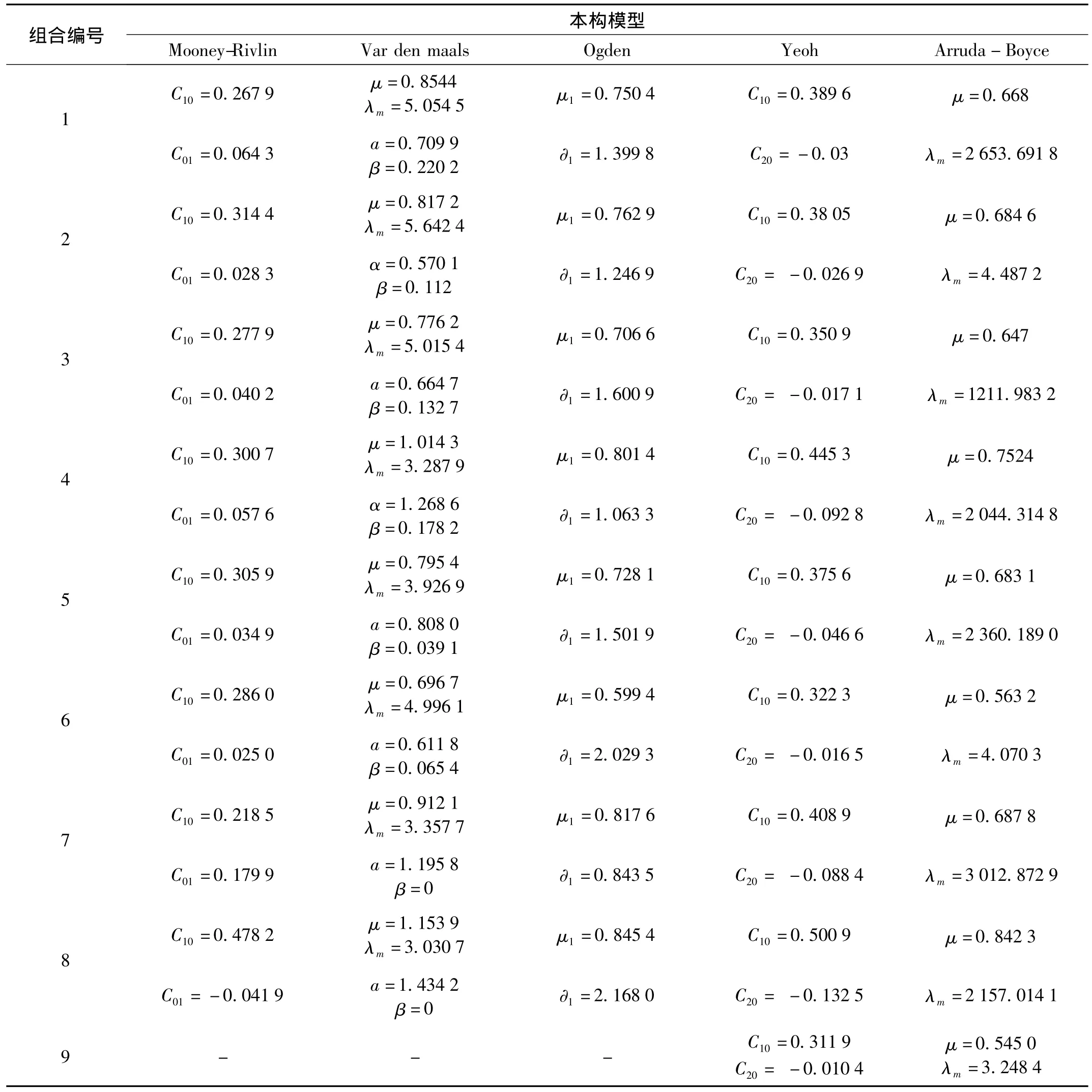
表2 各本构模型的材料常数Tab.2 The constitute constants in different constitute models

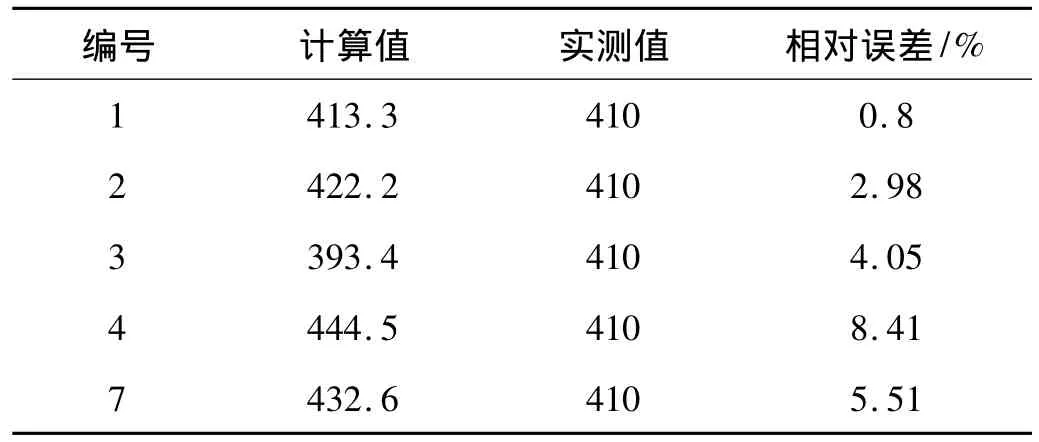
表3 X向静刚度计算值、实测值及其相对误差Tab.3 The estimated and experimental stiffness and their relative error in direction X

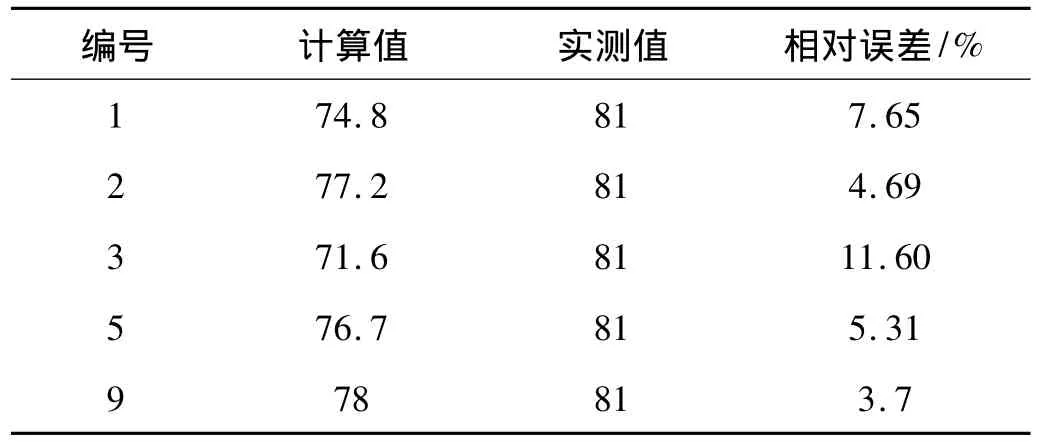
表4 Y向静刚度计算值、实测值及其相对误差Tab.4 The estimated and experimental stiffness and their relative error in direction Y

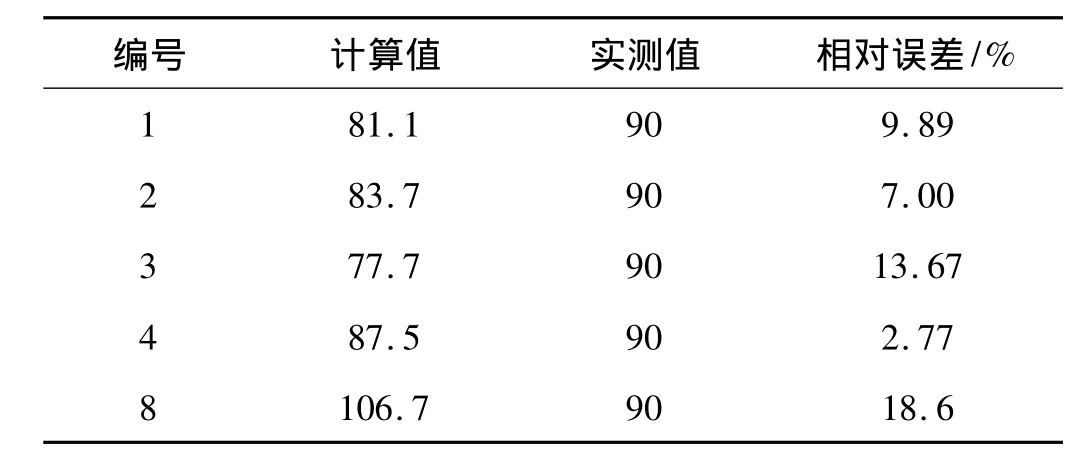
表5 Z向静刚度计算值、实测值及其相对误差Tab.5 The estimated and experimental stiffness and their relative error in direction Z

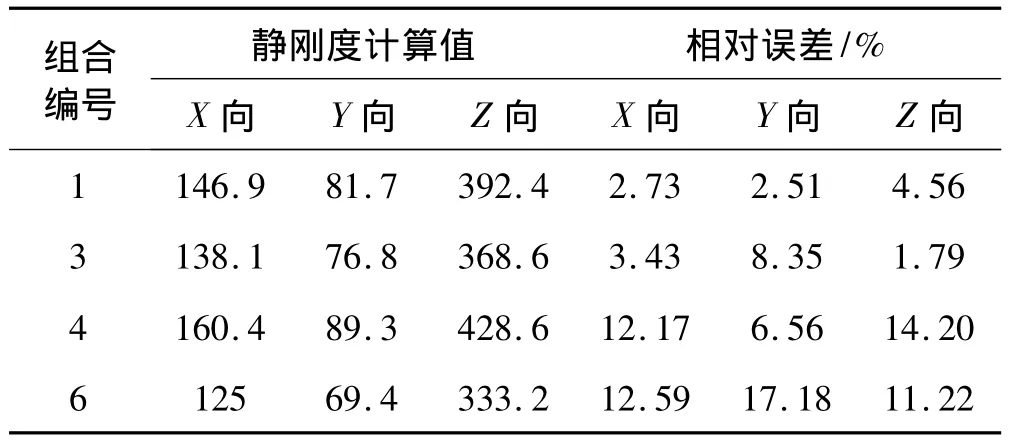
表6 利用Arruda-Boyce模型计算得到的悬置2的三向静刚度与实测值的相对误差Tab.6 The estimated and experimental stiffness and their relative error of mount II in three vertical directions using Arruda-Boyce mode

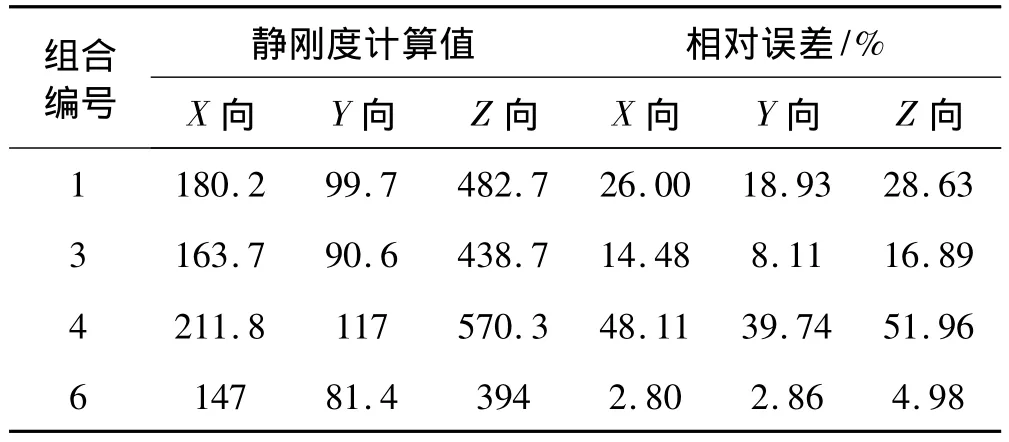
表7 利用Van der Waals模型计算得到的悬置2的三向静刚度与实测值的相对误差Tab.7 The estimated and experimental stiffness and their relative error of mount II in three vertical directions using Van der Waals mode

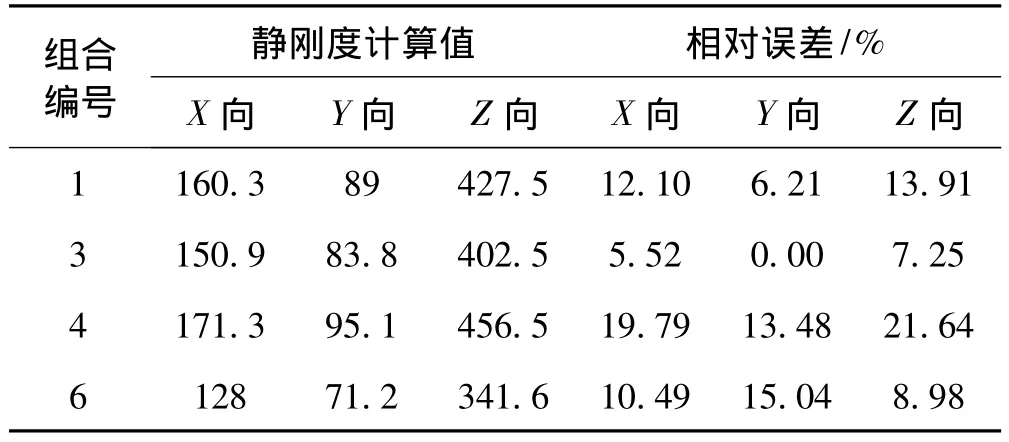
表8 利用Ogden模型计算得到的悬置2的三向静刚度与实测值的相对误差Tab.8 The estimated and experimental stiffness and their relative error of mount II in three vertical directions using Ogden mode

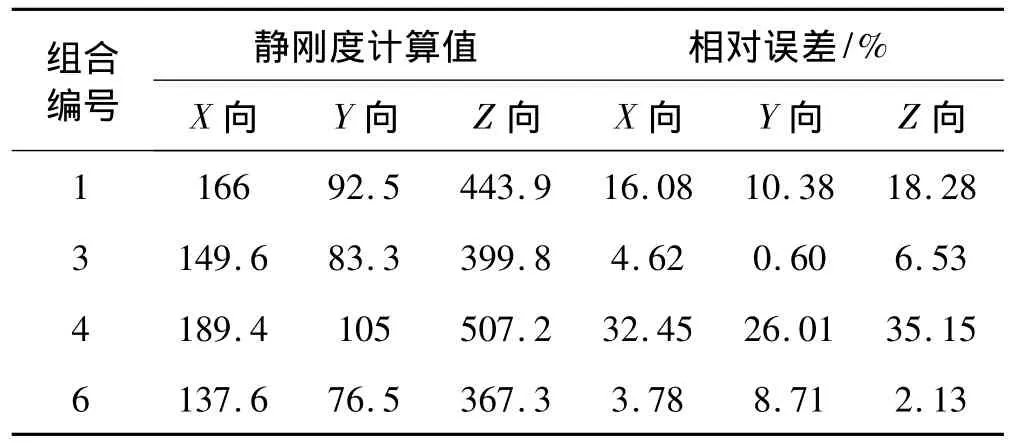
表9 利用Yeoh模型计算得到的悬置2的三向静刚度与实测值的相对误差Tab.9 The estimated and experimental stiffness and their relative error of mount II in three vertical directions using Yeoh mode

5 本构模型对力－位移特性计算结果的影响

在同种应力－应变状态组合下，用不同本构模型对悬置2进行静刚度计算并与实测值对比。选取1号、3号应力－应变组合下的计算结果进行分析，如图6所示。

由图6可见，用Mooney-Rivlin模型计算的悬置在X、Y和Z三向静刚度计算值与测试值最接近，其相对误差小于10%。用Van der Waals模型和Marlow模型计算得到的静刚度与实测值相对误差较大;利用Arruda-Boyce计算得到的静刚度与实测值吻合的较好，计算精度较高，大部分的静刚度计算值与实测值的相对误差小于10%。在3号应力－应变组合下，Ogden模型和Yeoh模型计算得到的静刚度与实测值相对误差小于10%。

由此可见，对于研究的几种本构模型，利用Mooney-Rivlin模型计算得到的悬置的静刚度计算值与实测值的相对误差最小。其次是Arruda-Boyce模型，误差最大的是Marlow模型和Van der Waals模型。

6 结论

根据以上计算结果，可得到如下结论:

(1)对于只受拉压变形的橡胶隔振器，用三种应力－应变状态比只用单轴拉伸应力－应变状态下拟合得到的本构模型常数计算得到的静刚度计算值精度高。对于只受剪切变形的橡胶隔振器，用平面剪切应力－应变状态比用三种应力－应变状态拟合得到的本构模型材料常数计算得到的静刚度精度高。

(2)对橡胶隔振器进行力－位移特性分析时，需选取合适的超弹性橡胶本构模型。本文的计算结果表明Mooney－Rivlin模型的计算精度最高，其相对误差均小于10%，其次是Arruda－Boyce模型，计算相对误差最大的是Marlow模型。在实际工程应用时，需要根据橡胶隔振器的结构特点以及受载情况，选取最适合的本构模型。

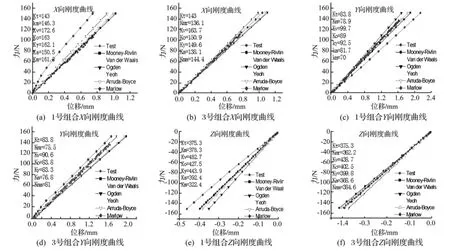
图6 利用三种应力－应变应变拟合得到的本构模型材料常数计算得到的悬置2三向力－位移关系(图中:Kt－测试刚度;Kmr－利用Mooney-Rivlin模型计算得到的刚度;Kv－利用Van der Waals模型计算得到的刚度;Ko－利用Ogden模型计算得到刚度;Ky－利用Yeoh模型计算得到的刚度;Ka－利用Arruda－Boyce模型计算得到的刚度;Kma－利用Marlow模型计算得到的刚度)Fig.6 The relation of force versus displacement for mount II calculated by the constitute constants obtained by the stress versus strain conditions(In this diagram，Kt stand for experiment stiffness，Kmr stand for estimated stiffness using Mooney-Rivlin model，Kv stand for estimated stiffness using Van der Waals model，Ko stand for estimated stiffness using Ogden model，Ky stand for estimated stiffness using Yeoh model，Ka stand for estimated stiffness using Arruda-Boyce model，Kma stand for estimated stiffness using Marlow model)

(3)利用不同的最大应变和不同的应力－应变状态组合得到的本构模型常数，对橡胶隔振器力－位移特性分析有很大影响。选取更接近实际变形状态的应力－应变状态，所计算出的橡胶隔振器的力－位移特性更准确。

［1］ Seibert D J，Schoche N.Direct comparison of some recent rubber elasticity models［J］. RubberChemistry and Technology，2000，73:366384.

［2］黄建龙，解广娟，刘正伟.基于Mooney-Rivlin模型和Yeoh模型的超弹性橡胶材料有限元分析［J］.橡胶工业，2008，55(8):467－470.

［3］Wang L R，Lu Z H.Modeling methods of constitutive law of rubber hyperelasticity based on finite elemen simulations［J］.Rubber Chemistry and Technology，2003，76(1):271 －285.

［4］Gracia L A，Liarte E，Pelegay J L，et al.Finite element simulation of the hysteretic behavior of an industrial rubber［J］.Application to Design of Rubber Components.Finite Elements in Analysis and Design，2010，46(4):357 －368.

［5］ Hartmann S， Tschope T， SchreiberL， etal. Finite deformations of a carbon black-filled rubber.Experiment，optical measurement and material parameter identification using finite elements［J］.European Journal of Mechanics，2003，22(3):309 －324.

［6］郭仲衡.非线性弹性理论［J］.北京:科学出版社，1980.

［7］ Morman K N，Nagtegall J C.Finite element analysis of viscoelastic elastomeric structures vibrating about non-linear statically stresses configurations［C］.SAE 811309.

［8］Shangguan W B，Lu Z H，Shi J J.Finite element analysis of static elastic characteristics ofthe rubberisolators in automotive dynamic systems［R］.SAE Technical Paper Series，2003，2003－01－0240.

［9］ ABAQUS ，Inc.Abaqus Analysis User's Manual［M］.2006.

［10］ Yeoh O H.On the Ogden strain-energy function［J］.Rubber Chemistry and Technology，1997，70(2):175 －182.

［11］杨晓翔.非线性橡胶材料的有限元单元法［M］.北京:石油工业出版社，1999:4.

［12］ Olsson A K.Finite element procedures in modelling the dynamic properties of rubber［D］. Lund:Lund University，2007.

［13］ Mullins L.Softening of rubber by deformation［J］.Rubber Chemical Technology，1969，42:339 －362.

［14］ Kim W D，Kim D J，Kim W S，et al，A study on the equibiaxial tension test of rubber material［J］.Korean Society of Mechanical Engineering，2003，11(5):95 －104.

［15］崔忠圻.金属学与热处理［M］.北京:机械工业出版，2001.

［16］潘孝勇.橡胶隔振器动态特性计算与建模方法的研究［D］.杭州:浙江工业大学，2009.