应用模态分析及傅里叶变换的柔性转子无试重动平衡方法

章 云，梅雪松，2，邹冬林，姜歌东，张东升

(1.西安交通大学 机械工程学院，西安 710049;2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

转子由于制造、安装误差以及材料的不均匀都会造成其或多或少的偏心，也就是存在不平衡量。转子的不平衡量在转子运转时会导致振动，振动若超过一定限制，不仅影响零件加工精度，还会对转子自身组件造成破坏，急剧减少转子系统寿命，甚至使某些组件由于振动量过大而当场损坏。因此，如何控制由于转子不平衡造成的振动是旋转机械使用过程中最为关键的问题之一。

转子不平衡振动在柔性转子中体现得尤为明显，作为其主要抑制手段，经典的柔性转子动平衡方法可大致分为二类，即模态平衡法［1－2］和影响系数法［3－4］。这二种方法各有利弊，模态平衡法平衡高阶振型时不影响低阶振型，启停次数相对较少，具有较高的敏感性，但需要知道转子的模态特性，平衡转速在临界转速附近，不易获得单一振型。影响系数法不受支承特性的影响，可同时平衡几阶振型，特别对轴系的平衡更为方便，但启停次数较多，高阶振型敏感性较低，还容易出现影响系数矩阵的病态化、平衡校正量不合理等问题。由于影响系数法与模态平衡法都存在一些难以克服的缺陷。学者们［5－6］提出了综合平衡的概念，该方法一定程度上结合了二者的优点，但依然需要在平衡过程中多次启停试重，若试重加载不当，反而造成转子剧烈振动，使动平衡操作复杂化，增加成本。

如果无须对试重就能准确知道转子的不平衡分布状态或者是有一定的预估，那么平衡过程会变得更加简单、安全。无试重动平衡方法正是基于该思提出的［7－8］。当前的无试重平衡方法或利用残余振动优化技术识别不平衡量，或通过动力学推导，建立不平衡力与转子振动之间的关系式，从而识别不平衡量。这些方法大多需要在一系列转速下采集信号，对于运行中的转子系统来说，转速变化意味着支承刚度的变化［9］，进而导致转子动力学行为发生改变。如果识别方法是在轴承刚度不变的假设下进行的，用基于变转速下采集的振动信号代入动力学模型进行不平衡分析就会引入误差，最终导致平衡精度的下降。此外，平衡转速与平衡风险是成正比的，低速动平衡也是动平衡技术发展的趋势。传统意义上的低速动平衡仅能使转子在刚性状态下获得平衡，当超过一阶临界转速后，新产生的振型不平衡需要通过高速动平衡加以消除。若在低速下(低于一阶临界转速)平衡转子，就可实现转子通过一阶临界转速后的平衡，或者至少减小柔性振型不平衡量，都将显著简化降低动平衡风险、提高动平衡效率。

总体来说，现有柔性转子动平衡方法或需要多次启停试重、或需要高速动平衡，这都给平衡操作增加了一定的难度。针对上述问题，本文立足于现有动平衡技术，提出一种利用模态分析和FFT变换思想，仅需在低于临界转速的状态下采集转子振动信号，无需停车试重，就可以识别柔性转子不平衡分布状态的方法。仿真和实验研究表明，该方法是行之有效的。

1 动力学模型

近年来，运用有限元理论分析转子的动力学特性取得了较好的效果［10］，典型的转子有限元模型由离散的质量盘、具有分布质量的轴段以及具有弹性的轴承座组成。因此可以沿轴线把主轴划分成质量盘、轴段和轴承座等单元，各单元间彼此在结点处联结。这些结点通常选在圆盘中心，轴颈中心及轴线的某些位置上。轴承座可简化为一个具有刚度和阻尼的弹簧。对于具有N个节点，其间用N－1个轴段连接而成的转子系统，设系统的位移向量为:

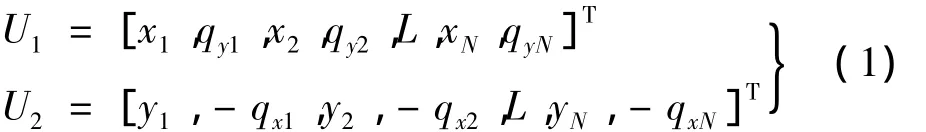
分别对各单元进行分析，可建立该单元节点力与节点位移间的关系，综合各单元的运动方程，如不计轴承座的等效质量，忽略阻尼时，可得到以节点位移为广义坐标的转子系统动力微分方程如下:

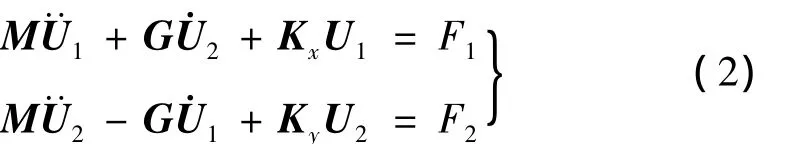
式中，M为质量矩阵，G为回转矩阵，Kx、Ky为刚度矩阵，Kx和Ky中包括了轴承的影响，F1、F2为相应的广义力。事实上，在广义力F1、F2中，由于各单元间相互作用的内力在方程综合过程中已经消去，同时轴承座对轴承的力也结合到了刚度矩阵中去了。广义力F1、F2中只剩下不平衡激励作用。

若忽略轴承各向异性，转子在X，Y两个方向上对称，有K=Kx=Ky。令:

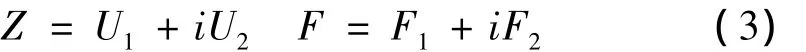
可得到整个系统的动力微分方程:

满足上述假设的案例是非常多的。对于那些不满足的情形，也可以把这些因素考虑进去，此时，动力学微分方程就要在水平方向和竖直方向分别求解。

2 不平衡求解

为了求解系统不平衡力，需要通过模态分析对系统运动微分方程进行解耦。若考虑回转矩阵G，则要进行复模态分析，此处旨在说明不平衡求解原理，为了书写简便，暂且不考虑 G的影响，式(3)可简化形式为:

要将转子的振动按模态振型展开，就需先将以物理坐标表示的运动微分方程，转换为以主坐标表示的运动微分方程，令:

其中，Z(t)为物理坐标，x(t)为模态坐标，Q(t)为主坐标下不平衡力，j为模态矩阵。将式(6)代入式(5)中，可将系统运动微分方程从物理坐标转换至主坐标上:

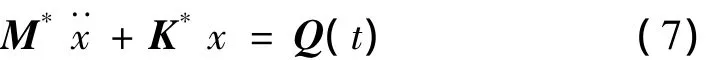
其中，M*为主质量矩阵，K*为主刚度矩阵。对式(7)作FFT变换，可得:

对式(6)作FFT变换，可得:

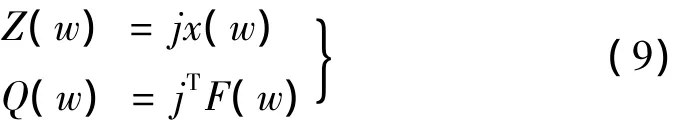
由于j不一定完备，通过对式(9)进行转换可以得出:

将式(10)代入式(8)中可得:

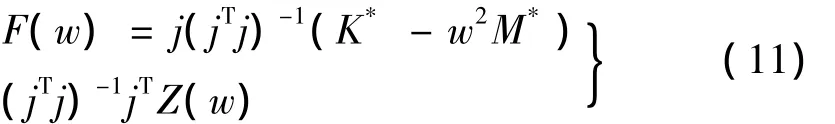
根据式(11)可求解物理坐标下的载荷谱F(w)，最后对F(w)作FFT逆变换即可获得时域内的待识别载荷。上述推导是没有考虑G的影响下的实模态分析，当考虑G的影响时，可用类似方法进行复模态分析。

在实际应用中，由于受到传感器布置条件的限制，不可能得到所有节点处的转子振动响应数据。此外，常见的旋转机械大多可以等效为质量集中结构，例如砂轮磨床的砂轮、航空发动机的叶片等，其不平衡量一般分布于某一截面。因此，有必要对算法做一些调整，使不平衡力的求解更为直观、简洁，利于实际应用中的推广。这里假设转子上布置有2个传感器，有2个质量盘。根据传感器所处节点的位置，可以取出这两个点的振动响应Z(t)21，同样，根据质量盘所处结点位置，可以取出这两个点的不平衡力q(t)21。在进行模态分析时，若取前二阶模态，则式(6)可变换为:

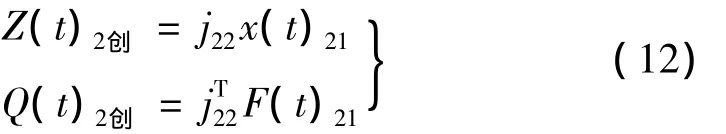
与前面推导过程相同，式(11)可变换为:

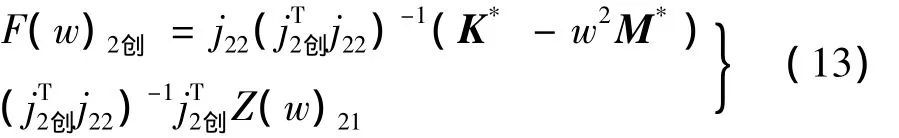
通过式(13)可获得频域下的不平衡载荷谱F(w)，经FFT逆变换就可求解时域状态下的不平衡力F(t)。

3 仿真分析

为验证算法的有效性，以本特利RK4转子实验台为原型，建立如图1所示的动平衡算法仿真模型。该动平衡模型由转子、轴承、质量圆盘三部分组成，其中，2个质量圆盘安装在转子上，转子振动响应由电涡流位移传感器采集，其安装在轴承与质量圆盘之间并靠近质量圆盘处。

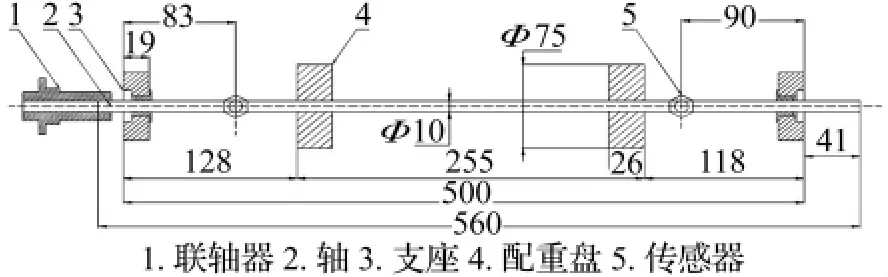
图1 仿真转子动力学模型Fig.1 Dynamic model of rotor system

把转子划分为44个单元，共45个结点，盘1在第14个结点处，盘2在第31个结点处，轴承1在第3个结点处，轴承2在第41个结点处。为了使有限元动力学模型更符合实际，尤其是获得准确的转子轴承处等效刚度值，可通过实测本特利RK4转子实验台的前两阶临界转速来修正理论模型。当轴承刚度值取1.2×106N/m时，通过模型可以计算得到转子前两阶临界转速分别为1 932 r/min和5 950 r/min，而实验测定转子前两阶临界转速分别为1 946 r/min和5 898 r/min，可见仿真结果与实测结果基本一致，间接验证了动力学模型的准确性。作为仿真分析，可人为地在转子2个圆盘上施加虚拟不平衡量如表1所示

表1 虚拟不平衡量幅值及相位Tab.1 Virtual imbalance distribution

设定平衡转速为1 500 r/min，在此转速下通过仿真模型获取振动响应，然后通过本文第2节所述算法，可以识别出两个质量圆盘上的不平衡量，识别结果如表2所示。

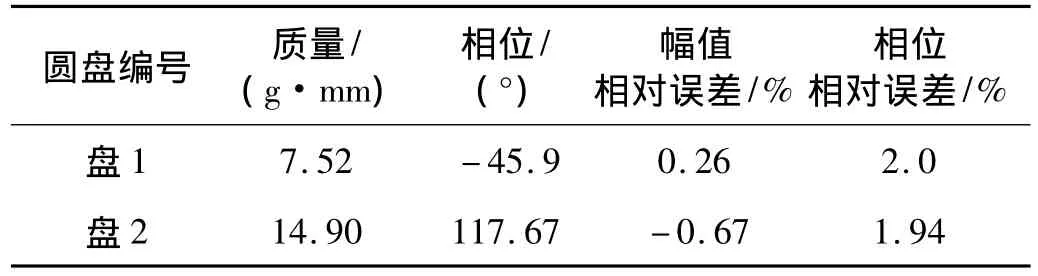
表2 识别的不平衡量Tab.2 Identification of imbalance

分别将表1所列的原始不平衡和表2所列的识别不平衡量代入动力学模型，求解传感器测量处的不平衡响应。结果如图2、图3所示，其中，图2为原始不平衡响应与识别不平衡响应的对比图，图3为原始不平衡响应与添加配重后剩余不平衡响应的对比图。

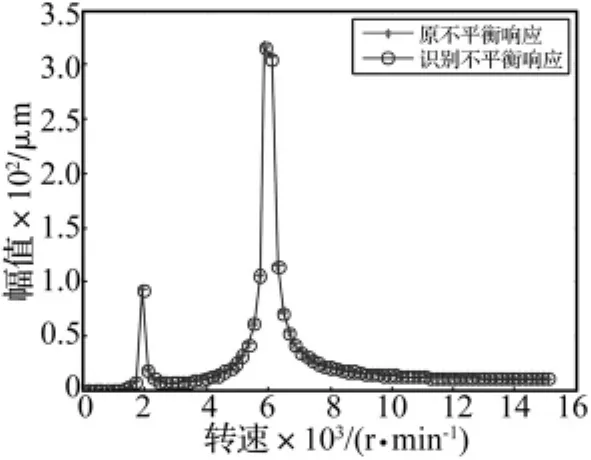
图2 原始不平衡响应与识别不平衡响应Fig.2 The given imbalance vibration and the identification imbalance vibration of rotor

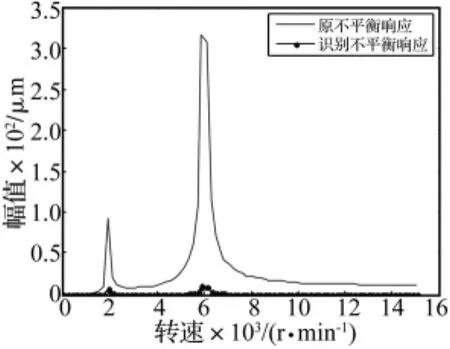
图3 原始不平衡响应与剩余不平衡响应Fig.3 The given imbalance vibration and the residual imbalance vibration of rotor

从上面的仿真分析可以看出，识别出的不平衡量幅值相对误差及相位相对误差在2%之内，其产生的振动效果与原始不平衡量基本一致，经过添加配重之后，剩余各阶不平衡响应较之原始不平衡响应大幅减小，这表明，本文所述算法可以准确地识别出转子的不平衡量。为了更进一步验证这种算法的有效性，课题还进行了实验分析。

4 实验验证

在仿真验证了算法的有效性之后，以本特利RK4转子实验台作为实验对像，对算法进行实验验证。图4为现场实验布局图，位移传感器布置在轴承与配重盘之间，并靠近配重盘一侧。为与仿真尽量保持一致，实验转速选定为1 500 r/min，并在该转速下采集振动数据，获取振动数据后代入式(13)中，即可求得不平衡量。因为该转子实验台在未使用之前就存在原始不平衡，所以在1 500 r/min时，先用经典动平衡方法将转子系统调整至平衡状态，然后在两个配重盘上人为施加不平衡量，最后通过本文所述的算法识别不平衡量，以便对比实验效果。

图4 实验现场布局图Fig.4 Experimental setup for measuring system

表3是人为施加在配重盘上的不平衡量信息，表4为识别出的2个配重盘上不平衡信息。

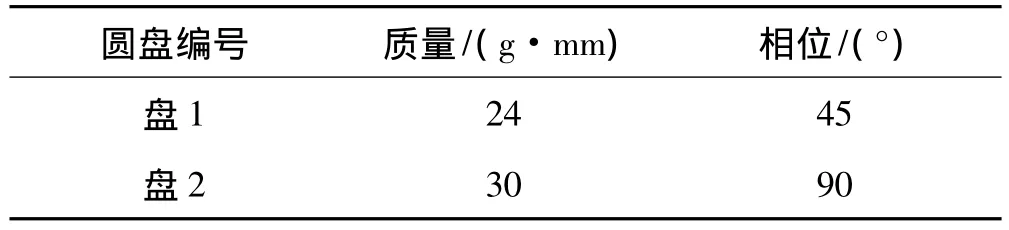
表3 圆盘上施加的不平衡量幅值及相位Tab.3 Imbalance distribution on counterweight disk

表4 识别的不平衡量Tab.4 Identification of imbalance

按表4所列的识别不平衡量在2个配重盘上添加配重后，可将原始不平衡响应与转子剩余不平衡响应进行比较，结果如图5所示。

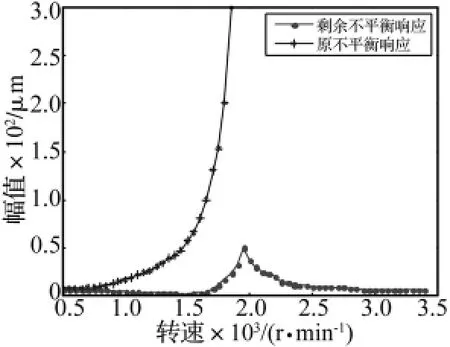
图5 原始不平衡响应与剩余不平衡响应Fig.5 The given imbalance vibration and the residual imbalance vibration of rotor

从图上可以看出，在未实施平衡时转子原始振动较大，在1 850 r/min时，转速已接近一阶临界转速，此时，传感器测量处的不平衡振动幅值约为300 μm，由于振动太大，出于安全考虑，实验时没有运行到一阶临界转速。在识别出不平衡，并在反方向加上不平衡配重后，在 1 500 r/min时，振动幅值由 56.8 μm 减小到2.5 μm，系统可以顺利通过一阶临界，且在达到一阶临界转速1 946 r/min时，振动幅值只有50 μm左右。从图5的对比中可以看出，本文所述算法能有效识别不平衡量，添加平衡配重后，系统临界前后残余振动都很小，这有力证明了算法的有效性。

从实验中可以看出，实验结果与仿真结果尚存在一些偏差，分析可能的误差来源主要有如下几点:

(1)动力学模型的精度不够。模型中没有考虑陀螺效应与阻尼的影响，这与实际存在一些偏差。

(2)本特利转子实验台加工精度不够。在对转子做动平衡时，残余振动最低只能调整到约2 μm。

(3)转子存在一定弯曲。从图5中可以看出，在转速低于1 500 r/min时，振动值主要由弯曲引起，而转速高于1 500 r/min时，不平衡引起的振动占了主要比重。

(4)振型体现不透彻。转子动平衡是在1 500 r/min时进行的，虽然此时转子振动受到一阶振型的影响，但是离一阶临界转速1 946 r/min仍有一定差距，获取的振动信息与一阶振型不是严格吻合。

5 结论

(1)转子作为旋转设备必要组件，其现场动平衡技术一直是研究的热点和难点，本文基于有限元动力学模型，采用模态分析和FFT变换技术，提出一种现场无试重动平衡识别方法。该方法能准确识别转子不平衡量，添加配重后，各阶振动得到有效抑制，理论仿真及实验研究证实了其可行性及有效性。

(2)该方法相比较于传统动平衡技术具有一定的优势，其仅需在低于临界转速的状态下采集振动数据，且测试过程中无需停机试重，就能完成柔性转子不平衡状态识别。该方法能有效降低动平衡操作风险，节约动平衡操作成本，具有较高的应用价值。

实际工程应用时，动平衡效果往往会受到多种因素的影响。在数据采集环节，可引入先进信号处理方法抑制信号噪声;建立系统动力学模型时，可采用理论与实验相结合的方式，提高模型精度;此外，为达到最小残余振动，可根据实际情况适当增加测振面及校正面数量。

［1］Kellenberger W.Should a flexible rotor be balanced in N or(N+2)planes?［J］.ASME J.Eng.Ind.，1972，94(2):548－560.

［2］Saito S，Azawa T.Balancing of flexible rotors by the complex modal method［J］.ASME J.Vib.，Acoust.，Stress，Reliab.Des.，1983，105:94 －100.

［3］Goodman T P.A least-square method for computing balance corrections［J］.ASME J.Eng.Ind.，1964，86:273 －279.

［4］Tessarzik J M，Badgley R H，Anderson W J.Flexible rotor balancing by the exact point-speed influence coefficient method［J］.ASME J.Eng.Ind.，1972，94:148 －158.

［5］Drechsler J.A combination of modal balancing and Influenee coefficient Method［C］.Proc.of World Congress on Theory of Machines and Mechanisms，Nelecastle-upon-Type，1975:81－86.

［6］ Darlow M S，Smalley A J，Parkinson A G.Demonstration of a unified approach to the balancing of flexible rotors［J］.Trans.ASME，J.Engr.Power，1981，103:101 －107.

［7］ Xu B，Qu L，Sun R.The optimization tehnique-based balancing of flexible rotors without test runs［J］.Journal of Sound and Vivration，2000，238(5):877 －892.

［8］ Ramlau R，Niebsch J.Imbalance estimation without test masses for wind turbines［J］.ASME Transactions，Journal of Solar Energy Engineering，2009，131:1 －7.

［9］Sinha J K，Friswel I M I，Lees A W.The identification of the unbalance and the foundation model of a flexible rotating machine from a single run down［J］.Mechanical Systems and Signal Processing.，2002，16(2 －3):255 －271.

［10］钟一谔，何衍宗，王 正，等.转子动力学［M］.北京:清华大学出版社，1987.