时间序列中随机型缺失数据的填补及预测效果比较*
2012-09-07李济宾张晋昕
李济宾 张 熙 张晋昕
时间序列中随机型缺失数据的填补及预测效果比较*
李济宾1,2张 熙3张晋昕1△
目的 本文旨在通过填补时间序列资料中的随机型缺失数据并拟合ARIMA模型,比较三种填补方法的填补和预测效果。方法 利用SAS产生平稳、有周期性的时间序列并构造不同比例的随机型缺失,分别采用周期性填补法、均值填补法和三次样条函数插值法进行缺失数据的填补,并对填补后序列拟合ARIMA模型进行序列预测。采用配对t检验对三种填补方法的填补误差和序列预测误差进行比较。结果 三种填补方法的填补值与真值的差异均无统计学意义(P>0.05);随着缺失比例的增大,周期性填补法的填补误差和序列预测误差均小于三次样条函数插值法和均值填补法。结论 周期性填补法对于含有确切周期信息的时间序列缺失数据,填补效果较优。
缺失数据 时间序列 填补 周期性 三次样条
1.中山大学公共卫生学院医学统计与流行病学系(510080)
2.香港中文大学公共卫生与基层医疗学院
3.复旦大学公共卫生学院卫生统计与社会医学教研室(200032)△通讯作者:张晋昕,E-mail:zhjinx@mail.sysu.edu.cn
缺失数据是医学应用研究中普遍存在的实际问题。在对医学时间序列数据进行建模预测时,序列的长度和完整性对拟合模型的可靠性有影响。医学时间序列的观测值具有不可重复的特点,缺失数据的随意插补或跳过,使拟合的模型难以很好地反映纵向数据的规律,制约了时间序列在医学领域的应用。因此,如何合理填补时间序列资料中的缺失数据,进而拟合合适的数学模型是医学时间序列应用中需要解决的一个重要问题。
目前,针对时间序列缺失数据处理的技术主要基于时域信息,如删除法、均数填补法、极大似然估计法、三次样条函数插值法等〔1,2〕。实践表明,三次样条函数插值法是一种思路简明、效果较优的补缺方法。这些方法共有的一个缺陷是,未能利用时间序列中蕴含的周期信息。为此,本文探讨一种基于序列周期信息,以不同周期的谱峰值作为权重的缺失数据填补方法,并利用模拟时间序列数据考核其填补效果。
资料与方法
1.模拟序列
在SAS9.1的软件环境下,利用正弦函数Y=abs(sin(ωx))和正态分布函数 ε=μ+sqrt(σ2)×rannor(seed),模拟产生μ=0,σ2=1,随机波动水平的月度时间序列,序列的周期设置为3、6和12个月。序列的起始时间设为1962年1月1日。模拟序列长度设置为N=300。
随机型缺失数据的构造:利用SAS为模拟时间序列数据产生正态分布的随机数,根据随机数的秩次依次将缺失数据的比例设置为5%,10%,15%,20%,25%,30%,35%,40%共8个档次。
2.缺失数据填补方法
(1)均值填补法:以序列均数作为缺失数据的填补值。
(2)三次样条函数插值法〔2〕
三次样条函数插值法是时间序列中缺失数据填补的常用方法之一。设函数f(x)在给定区间[a,b]上有定义,其中a=x0<x1<…<xn=b是给定的n+1个插值节点,若S(x)满足条件:①S(x)在每个小区间[xj,xj+1]上是三次多项式;②S(x)在每一个内节点上,S(x)∈C2[a,b];③S(x)在所有节点内满足S(xj)=f(xj)。则称S(x)是节点x0,x1,…,xn上的三次样条函数。为了构造特定的样条插值函数,还需增加边界条件的限制。边界条件可根据实际情况来确定,不同边界条件下S(x)的表达式可以有多种表现形式。本文针对时间序列的三次样条函数插值法,由SAS9.1软件环境下的PROC EXPAND过程实现〔3〕。
(3)基于序列周期信息的填补法(下文简称作周期性填补法)
①以序列均值作为缺失数据的初始填补值;②利用周期图峰值检验的方法搜索序列中有统计学意义的m个隐周期,用I1,I2,…,Im表示对应周期的谱峰值;③基于m个周期,分别计算不同周期位置上序列的均数,将第i个缺失位置上的m个均数记为Xi(1),…,Xi(m);④ 以周期峰值I1,I2,…,Im作为权重,获得第i个缺失位置的加权填补值Xi:

式中i表示缺失数据序号i=1,2,…,n,j表示隐周期序号j=1,2,…,m;
⑤用步骤④中填补后的完整序列,重复步骤②、③和④,直到前后两次填补值的相对改变量δ≤0.01或迭代次数大于100次时,停止迭代,获得缺失数据的最终填补值。本文通过搜索周期图的峰值个数来确定隐周期的初始个数r,周期性检验的方法采用Priestley(1981)和Chiu(1989)提出的检验统计量〔4〕。
3.填补效果比较
(1)填补误差
采用均方根误差(RMSE)和平均绝对误差〔5〕(MAE)量化填补值与真实值之间的填补误差。
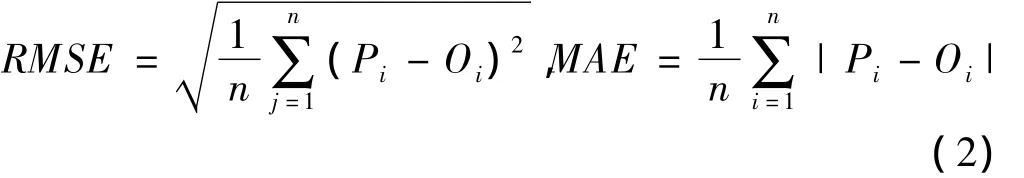
其中,n为缺失数据序号i=1,2,…,n,Pi表示填补值,Qi表示真实值。
以缺失个数n为样本量,用配对t检验比较各填补方法的填补值与真值的差异;同时调整检验水准为α'=α/2=0.05/2=0.025,比较均值填补法、三次样条函数插值法与周期性填补法的绝对填补误差(|真实值-填补值|)的差异。
(2)绝对预测误差
采用自回归移动平均求和模型进行时间序列的模型拟合及序列预测,简记为 ARIMA(p,d,q),其表达式为〔6〕:
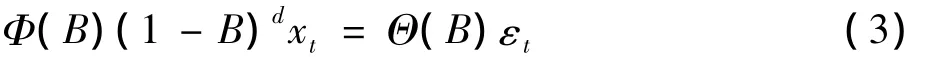
式中,p和q分别表示自回归和移动平均的阶数,d为差分的阶数,Φ(B)=1-φ1B-…-φpBp,为p阶自回归系数多项式。Θ(B)=1-θ1B-…-θqBq,为q阶移动平均系数多项式。
按照时间顺序逐段选择观测长度为120的序列片段,进行提前期l=1~12的预测(即t1=1~120,t2=2~121,…),直至预测末期观测值为时间序列的末值,确保能够从实测值得到预测误差。以推移次数(n')作为样本量,以三种方法的绝对预测误差(绝对预测误差=|真实值-预测值|)作为变量,进行配对t检验,比较均值填补法、三次样条函数插值法与周期性填补法绝对预测误差的差异(其中检验水准调整为α'=α/2=0.05/2=0.025)。绝对预测误差小的填补方法,其填补效果较优。
结 果
1.不同缺失比例下三种方法的填补值与真值的差异
表1结果显示,三种方法的填补值与真值之间的差异均无统计学意义(P>0.05)。进一步绘制不同缺失比例下,三种方法填补值的平均误差线图。图1显示,周期性填补方法的曲线与参考线间的距离最小,而三次样条函数插值法的曲线与参考线间的距离最大。
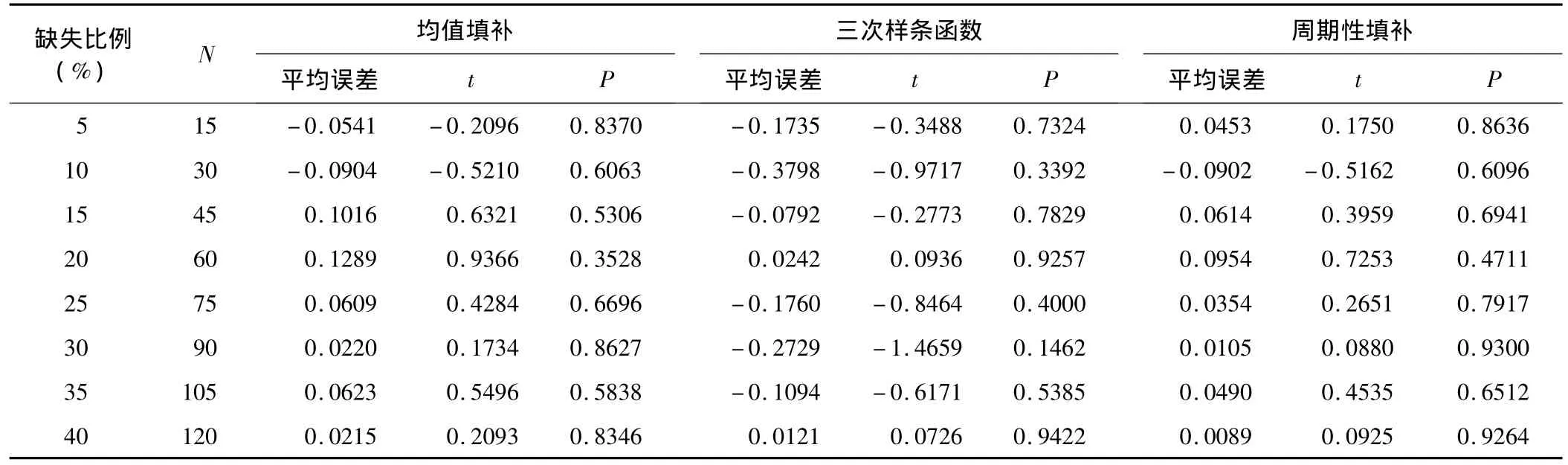
表1 不同缺失比例下三种方法的填补值与真值的比较
2.不同缺失比例下三种方法填补误差的比较
表2为均值填补法、三次样条函数插值法与周期性填补法的绝对填补误差的比较结果。当缺失比例大于15%时,周期性填补法的绝对误差小于均值填补法(P<0.025);此外,在各缺失比例下,周期性填补法的绝对误差均小于三次样条函数插值法对应的绝对误差(P<0.025)。
图2为不同缺失比例下,三种填补方法填补值的平均绝对误差(a)和均方根误差(b)的曲线图,周期性填补方法的平均绝对误差和均方根误差的曲线均始终位于均值填补法和三次样条函数插值法所对应曲线的下方。
3.缺失数据填补后序列拟合模型的预测误差比较
为了进一步比较三种方法的填补效果,由序列自相关函数和偏自相关函数,对模拟时间序列进行模型识别,最终确定原始序列的模型形式为:
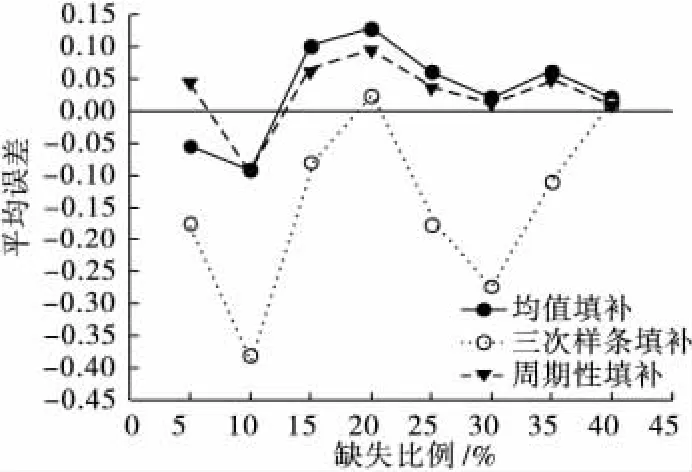
图1 不同缺失比例下三种填补方法填补值的平均误差
利用此模型对三种方法填补后的完整序列建模并进行提前期l=1~12的预测。在中期(l=6)和远期(l=12)的预测中,除缺失比例等于10%的情况,周期性填补法填补序列对应的预测误差均小于均值填补法和三次样条函数插值法。此外,在近期(提前期l=1)的预测中,当缺失比例大于10%时,周期性填补法填补序列对应的预测误差小于均值填补法。

*:1:三次样条函数与周期性填补;2:均值填补与周期性填补。
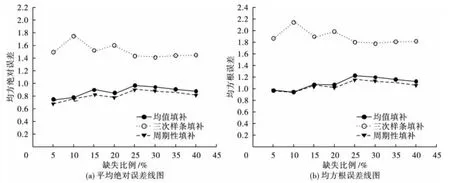
图2 三种填补方法的平均绝对误差、均方根误差随缺失比例变化的线图
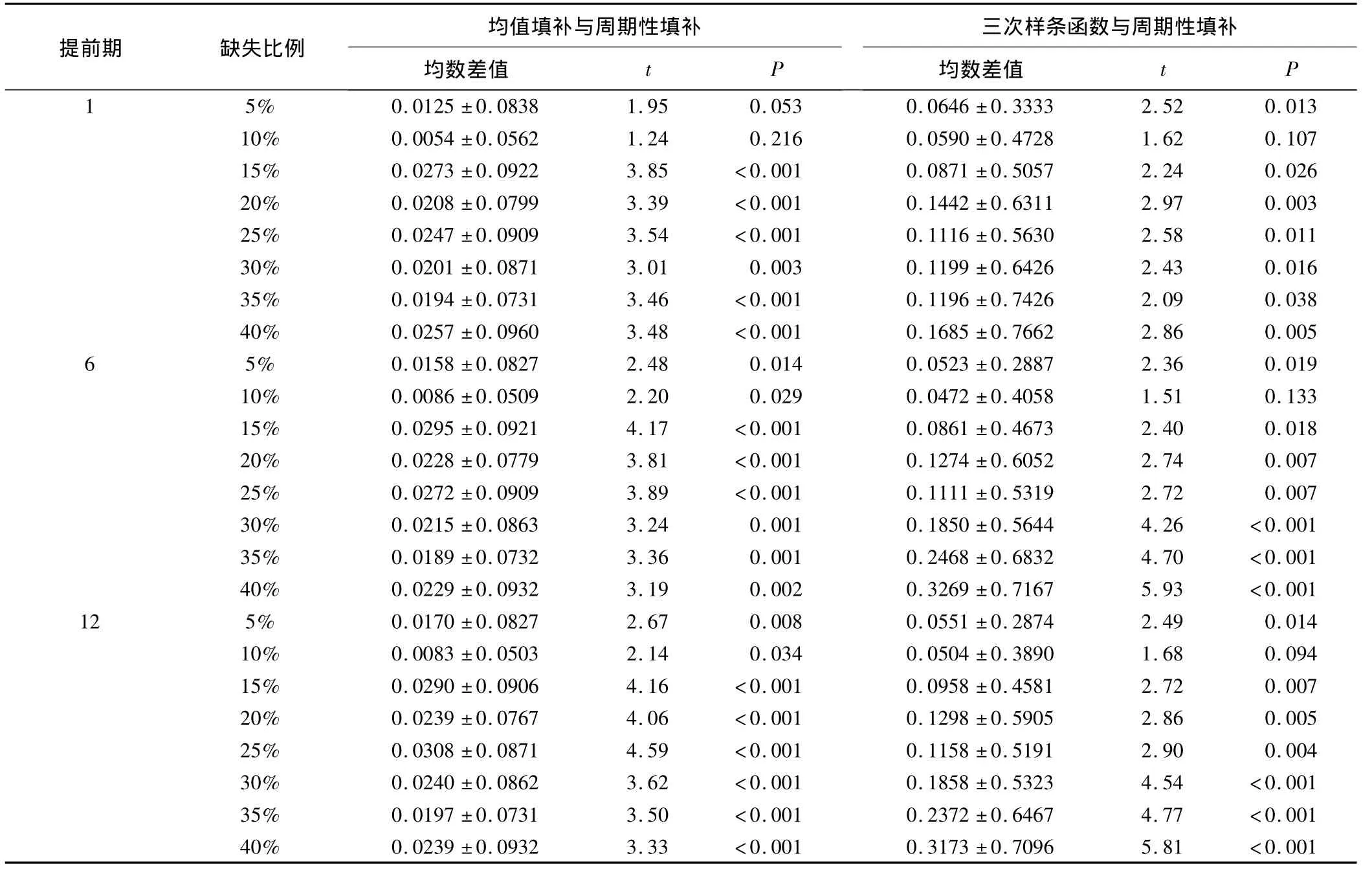
表3 提前1、6、12期时三种填补方法在各缺失比例下的预测绝对误差 (n'=169)
图3显示,在缺失比例小于10%的情况下,三种方法的绝对预测误差的差别不大;随着缺失比例的增大,三次样条函数插值法的绝对预测误差呈上升趋势;均值填补法和周期性填补法的绝对预测误差均减小。同时,趋势图显示周期性填补法所对应预测误差的曲线始终位于均值填补法和三次样条函数插值法所对应曲线的下方。

图3 不同缺失比例下,三种填补方法提前期l=1、6、12的平均绝对预测误差变化趋势
讨 论
时间序列数据是按照时间顺序取得的一系列观测值,其典型的特征是相邻观测值之间存在相关性,使得时间序列观测值相互间不独立,从而致使通常的针对独立数据的缺失数据填补方法在时间序列中不再适用。
本文针对基于时间序列周期信息的缺失数据加权填补方法〔7〕,利用模拟数据从填补误差和预测误差两个方面对填补方法的填补效果进行考核。结果显示,三种方法的填补值均可以较好地估计出真实值,同时缺失比例大于15%时,周期性填补法的填补误差是三种方法中最小的。在提前期l=1、6、12的预测中,缺失比例大于10%以后,周期性填补法填补序列的预测误差小于均值填补法和三次样条函数插值法。此外,对于均值填补法,由于样本均数在不同位置的多次出现,容易导致低估变量的变异程度,进而扭曲原始样本的分布状态〔8-9〕。
综上所述,结合时间序列的周期信息,进行加权填补的效果优于普通的只利用时域信息的缺失数据填补方法,尤其是对于缺失比例较大的情况。另外,需要说明的是,周期性检验是“周期性填补法”的关键步骤之一,对于未蕴涵确切周期信息的时间序列,周期性填补法将不再适用。
1.Wayne FV,Suzanne MC.A comparison of missing-data procedures for ARIMA time-series analysis.Educational and Psychological Measurement,2005,65(4):596-615.
2.郭昌言,高尚.三次样条函数插值的推广.科学技术与工程,2011,11(7):1507-1509.
3.高惠璇等编译.SAS系统SAS/ETS软件使用手册.北京:中国统计出版社,1998,232-252.
4.Michael Arits,Mathias Hoffmann.The detection of hidden periodicities:a comparison of alternative methods.Paper provided by European University Institute in its series Economics WorkingPapers with number ECO2004/10.
5.Heikki Junninena,Harri Niskaa,Kari Tuppurainenc,et al.Methodsfor imputation of missing values in air quality data sets.Atmospheric Environment.2004(38):2895-2907.
6.肖枝洪,郭明月.时间序列分析与SAS应用.武汉:武汉大学出版社,2009,44-109.
7.张熙.基于周期信息的时间序列缺失值填补方法研究.广州:中山大学,硕士学位论文,2009.
8.RK Kunar,RM Chadraseker.Missing data imputation in cardiac dataset(survival prognosis).IJCSE,2010,2(5):1836-1840.
9.王睿.胃食管反流病流行病学调查及其缺失数据的处理方法研究.上海:第二军医大学,博士学位论文,2009.
Prediction and Imputation for Missing Data at Random in Time Series
Li Jibin,Zhang Xi,Zhang Jinxin.School of Public Health,Sun Yat-sen University(510080),Guangzhou
ObjectiveIt is aimed to compare the effects of interpolation and prediction by imputing the missing data at random and fitting proper ARIMA models in time series.MethodsMissing data at random are generated with different missing proportions in simulated stationary time-series with periodicity.And then the missing data are interpolated using mean imputation,the cubic spline imputation and imputation based on periodicity.Prediction for imputed time-series is carried out by fitting a proper ARIMA model.The differences of interpolation and prediction from truth-data were analyzed using paired t test.ResultsThe differences between interpolation and truth-data were of no statistical significance.Both absolute interpolation errors and prediction errors in imputation based on periodicity were less than those of the cubic spline imputation and the mean imputation.ConclusionThe imputation based on periodicity showed better efficiency for missing data at random in time series with significant periodicity.
Missing data;Time series;Imputation;Periodicity;Cubic spline
2008年国家自然科学基金资助(30872182)
