GAM识别非线性相关及其在医学统计建模中的应用*

北京大学生育健康研究所/卫生部生育健康重点实验室(100191) 李宏田 袁 悦 李智文 王琳琳 刘建蒙

GAM识别非线性相关及其在医学统计建模中的应用*

北京大学生育健康研究所/卫生部生育健康重点实验室(100191) 李宏田 袁 悦 李智文 王琳琳 刘建蒙△

目的 介绍广义相加模型(GAM)识别非线性相关及其在医学统计建模中的应用。方法 应用SAS软件PROC GAM模块识别实例数据结局变量与自变量之间的非线性相关，通过比较考虑该非线性相关和不考虑该非线性相关时多元线性回归和logistic回归模型的拟合和预测效果，阐明GAM识别非线性相关在统计建模中的重要性。结果 与不考虑非线性相关的模型相比，考虑非线性相关的模型拟合和预测效果更优。结论 合理使用GAM，在模型中纳入非线性成分，可改善回归模型的建模效果和预测精度。

广义相加模型 非线性相关 统计建模

*:国家自然科学基金面上项目(编号:81072372)和科技部973项目(编号:2007CB5119001)资助

△通讯作者:刘建蒙，E-mail:liujm@pku．edu．cn

广义相加模型GAM，于1986年由Hastie和Tibshirani提出〔1，2〕。GAM 是对传统广义线性模型(包括多元线性回归和logistic回归模型)的扩展。广义线性模型一般形式为E(Y|X1，X2，…，Xp)= β0+ β1X1+β2X2+… +βpXp，而 GAM 一般形式是E(Y|X1，X2，…，Xp)=β0+f1(X1)+f2(X2)+… +fp(Xp)。fp(Xp)是关于Xp的非指定类别的非参数函数，其估计方法有平滑样条法(smoothing splines)、局部加权回归散点平滑法(LOESS)和薄盘平滑样条法(thin-plate smoothing spline);平滑参数选择的方法有交叉验证(cross validation)或广义交叉验证(generalized cross validation)。SAS软件设有专门的GAM模块，是GAM建模常用软件之一〔3〕。本文将采用SAS软件PROC GAM模块识别实例数据结局变量与自变量之间的非线性相关，通过比较考虑该非线性相关和不考虑该非线性相关时多元线性回归和logistic回归模型的拟合和预测效果，阐明GAM识别非线性相关在统计建模中的重要性。

实例数据

实例数据是关于儿童智商(IQ)影响因素的研究资料，于2000年收集，样本量为7340;变量及其分布见表1。建模时文化程度(EDU)按哑变量进入模型;以初中及以下组为参照，大专及以上、高中或中专和不详组对应的哑变量依次为EDU1、EDU2和EDU3。

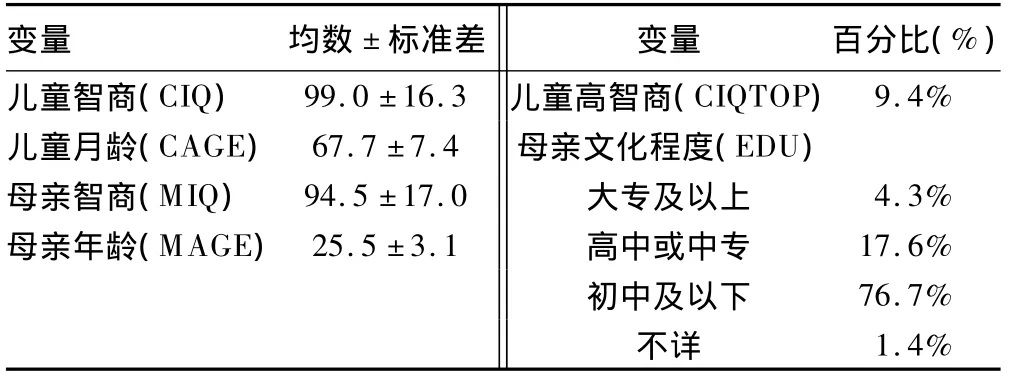
儿童智商(CIQ) 99．0±16．3 儿童高智商(CIQTOP) 9．4%)儿童月龄(CAGE) 67．7±7．4 母亲文化程度(EDU)母亲智商(MIQ) 94．5±17．0 大专及以上 4．3%母亲年龄(MAGE)25．5±3．1 高中或中专 17．6%初中及以下 76．7%不详 1．4%

模型拟合和评价方法

7340名儿童随机分成数据集IQSAMPLE(n=3687)和IQTEST(n=3653)。IQSAMPLE用于建模，IQTEST用于预测评价。先以CIQTOP为因变量，以CAGE，MAGE，MIQ和EDU为自变量建立logistic回归模型1;进而通过GAM识别CIQTOP与CAGE，MAGE和MIQ之间是否有非线性相关以及非线性相关的具体类型，并将其引入logistic回归模型，建立模型2。利用赤池信息准则(AIC)比较模型1和2的建模效果，AIC值越小，建模效果越好。比较模型1和2用于IQSAMPLE预测时KAPPA统计量的最大取值，KAPPA值越大，建模效果越好;将IQTEST分别回代至模型1和2，以前述KAPPA值最大时的判别概率为标准，比较两个模型用于IQTEST预测的KAPPA值。再以 CIQ为因变量，以 CAGE，MAGE，MIQ和 EDU为自变量建立多元线性回归模型1和2，建模过程与logistic回归建模类似，也利用AIC比较模型1和2的建模效果。将IQTEST分别回代至模型1和2，比较两个模型残差平方和的大小，残差平方和越小，建模效果越好。

SAS程序与建模评价

1．logistic回归建模

PROC LOGISTIC DATA=IQSAMPLE DESC;MODEL CIQTOP=EDU1 EDU2 EDU3 MIQ CAGE MAGE;RUN;

logistic回归模型 1的 AIC值为 1984.02，对IQSAMPLE预测的最大KAPPA值为0．305，相应的判别概率为0．23;据此概率值，模型1用于IQTEST预测的KAPPA值为0．307。参数估计结果见表2。

(2)GAM识别非线性相关

①程序及主要结果

PROC GAM DATA=IQSAMPLE;MODEL CIQTOP=PARAM(EDU1 EDU2 EDU3)SPLINE(MIQ)SPLINE(MAGE)SPLINE(CAGE)/DIST=BINOMINAL;QUIT;

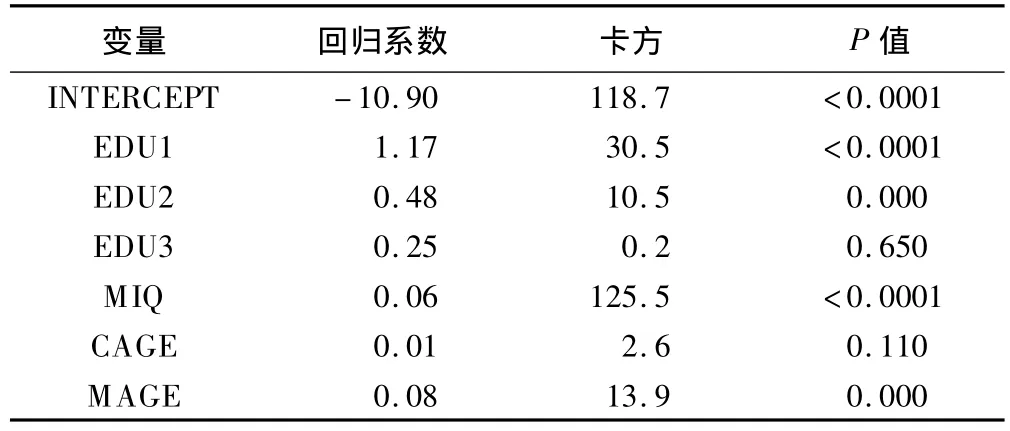
表2 logistic回归模型1参数估计

调用 GAM程序，拟合 IQSAMPLE数据集，以CIQTOP为因变量，EDU以哑变量形式按参数函数〔PARAM(变量名)〕进行拟合，MIQ、MAGE和CAGE按非参数函数〔SPLINE(变量名)〕进行拟合。DIST指定CIQTOP呈二项分布(BINOMINAL)。GAM程序拟合非参数函数默认自由度为4，线性部分为1，非线性部分为3。SAS主要输出结果见表3－5，第1部分与模型1参数估计基本一致，仅CAGE检验的P值由0．11变为0．07。第3部分MAGE非线性部分检验有统计学意义，即MAGE与IQTOP呈非线性相关。

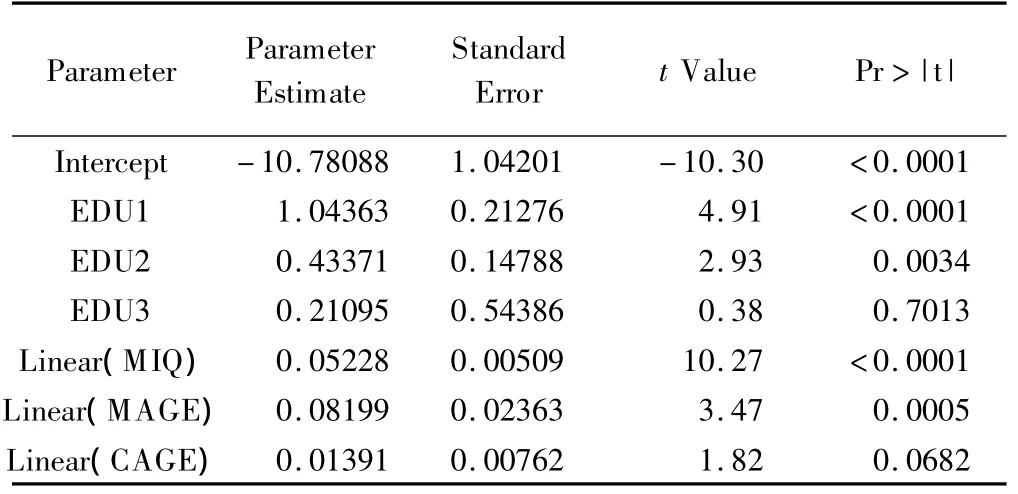
表3 GAM参数函数及非参函数线性部分估计结果

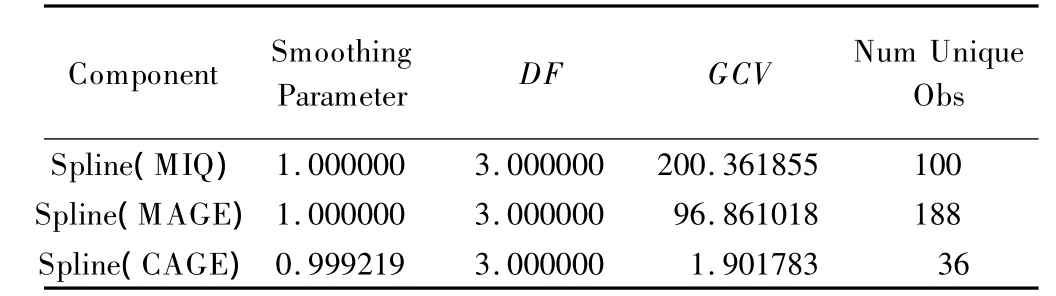
表4 GAM非参数函数非线性部分平滑拟合结果

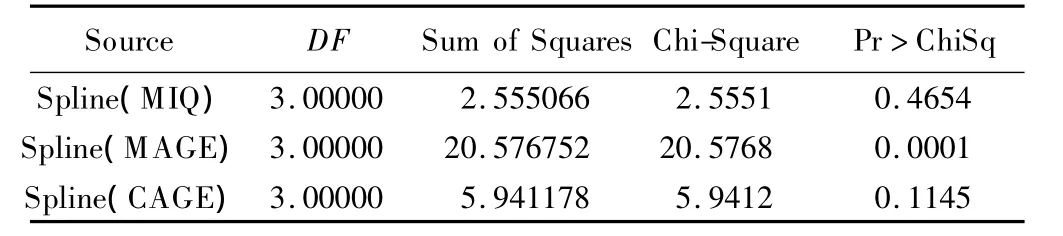
表5 GAM非参数函数非线性部分假设检验结果

②程序及主要结果

2017年互联网期刊出版行业的主要出版商仍然是以同方知网（北京）技术有限公司（以下简称同方知网）、万方数据科技有限公司（以下简称万方数据）、重庆维普资讯有限公司（以下简称维普资讯）、龙源数字传媒集团（以下简称龙源数媒）四家出版企业占市场最大份额，还有其他出版企业也开始接触互联网期刊业务。

PROC GAM DATA=IQSAMPLE;MODEL CIQTOP=PARAM(EDU1 EDU2 EDU3)SPLINE(MIQ)SPLINE(MAGE)SPLINE(CAGE)/METHOD=GCV DIST=BINOMINAL;QUIT;

程序①拟合非参数函数默认自由度为4;程序②增加了METHOD=GCV语句，指定参数估计方法为广义交叉验证法，不限定自由度。参数函数及非参数函数线性部分的拟合结果与程序1基本一致，非参数函数非线性部分的假设检验仍显示MAGE与CIQTOP呈非线性相关，CAGE非线性部检验的P值减小至0.053，提示CAGE与CIQTOP呈非线性相关(表6)。

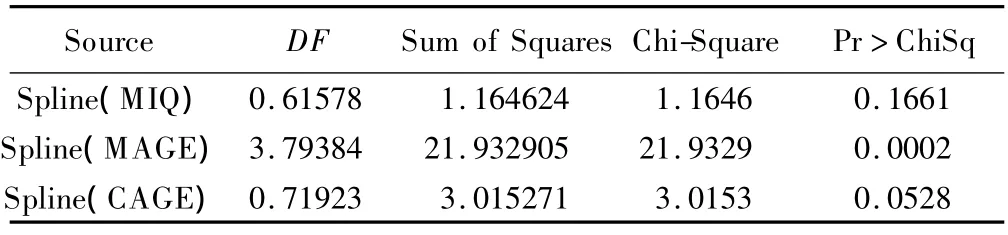
表6 广义交叉验证法GAM假设检验结果

③程序及主要结果

ODS HTML;ODS GRAPHICS ON;PROC GAM DATA=IQSAMPLE PLOT(CLM);MODEL CIQTOP=PARAM(EDU1 EDU2 EDU3)SPLINE(MIQ)SPLINE(MAGE)SPLINE(CAGE)/METHOD=GCV LINK=LOGIT DIST=BINOMINAL;QUIT;ODS GRAPHICS OFF;ODS HTML CLOSE;

程序②显示MAGE和CAGE与CIQTOP均呈非线性相关，程序③增加了ODS GRAPHICS和PLOT(CLM)语句，该语句会输出非参数函数非线性部分对CIQTOP影响的效应图，见图1。MAGE和CAGE非参数函数非线性部分对CIQTOP影响近似于二次方曲线，MAGE曲线开口向下，CAGE曲线开口向上。基于此曲线，预期在Logistic回归模型中增加MAGE和CAGE的二次方项会改善建模和预测效果。

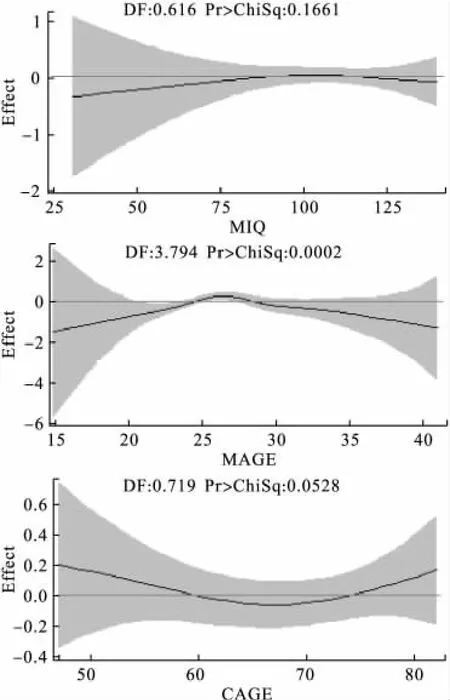
图1 GAM SAS程序③的部分输出结果

(3)logistic回归模型2的SAS程序及主要结果PROC LOGISTIC DATA=IQSAMPLE DESC;MODEL CIQTOP=EDU1 EDU2 EDU3 MIQ CAGE CAGE*CAGE MAGE MAGE*MAGE;RUN;

logistic回归模型 2的AIC值为 1970.66，对IQSAMPLE预测的最大KAPPA值为0.324，相应的判别概率为0.22;据此概率值，模型2用于IQTEST预测的KAPPA值为0.349。参数估计结果见表7。模型2的AIC值小于模型1，对IQSAMPLE和IQTEST预测的最大KAPPA值均大于模型1，表明模型2优于模型1。MAGE二次方项检验有统计学意义，CAGE二次方项检验的P值为0.06，接近有统计学意义;回归系数符号所反映的开口方向与GAM输出的MAGE和CAGE非线性部分效应图相吻合。

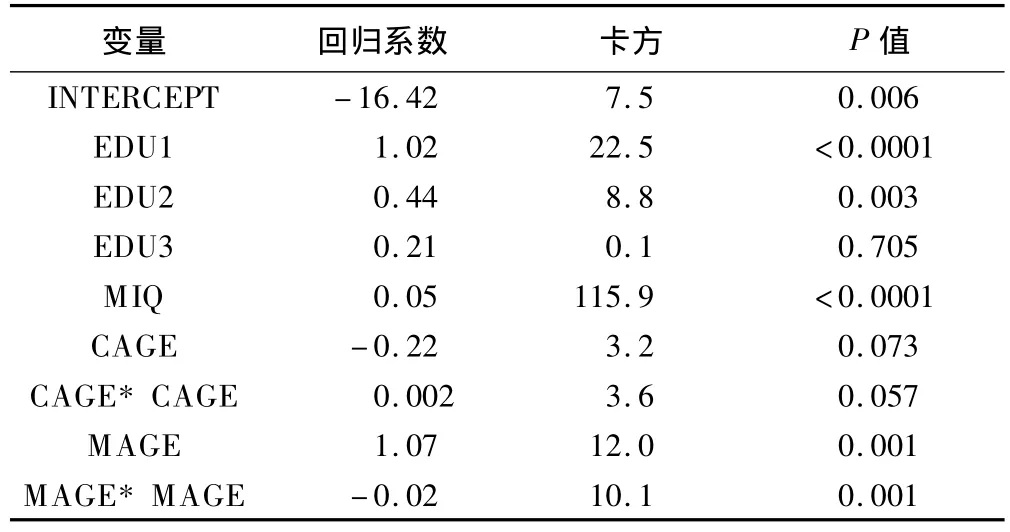
表7 logistic回归模型2参数估计

多元线性回归建模

1．多元线性回归模型1的SAS程序及主要结果

PROC REG DATA=IQSAMPLE;MODEL CIQ=EDU1 EDU2 EDU3 MIQ CAGE MAGE;QUIT;

多元线性回归模型1的AIC值为19614.33，对IQSAMPLE预测的残差平方和为 750603.39，对IQTEST预测的残差平方和为728649．26;参数估计结果见表8。

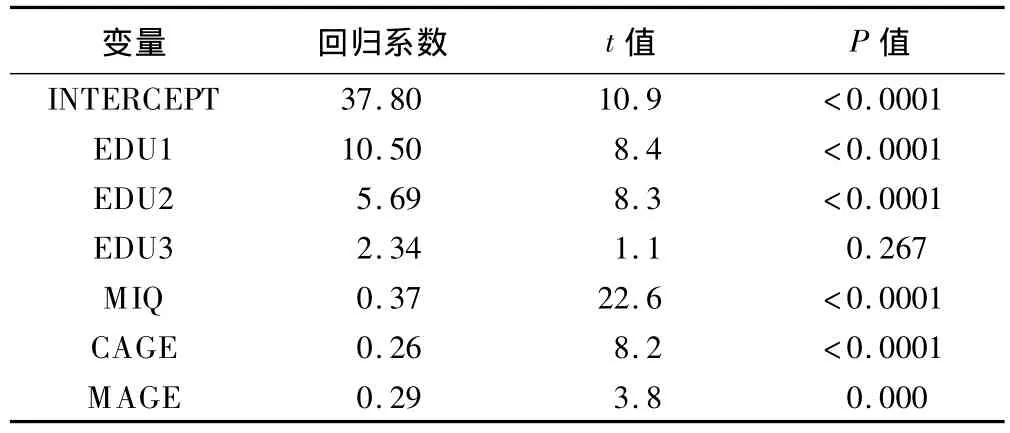
表8 多元线性回归模型1参数估计

2．GAM 非线性相关识别

(1)程序及主要结果

PROC GAM DATA=IQSAMPLE;MODEL CIQ=PARAM(EDU1 EDU2 EDU3)SPLINE(MIQ)SPLINE(MAGE)SPLINE(CAGE)/DIST=GAUSSIAN;QUIT;

调用GAM程序，拟合IQSAMPLE数据集，以CIQ为因变量，EDU以哑变量形式按参数函数进行拟合，按默认自由度(df=4)对MIQ、MAGE和CAGE进行非参数函数拟合。DIST指定CIQ的分布为高斯分布(GAUSSIAN)，默认的连接函数为IDENTITY。结果见表9－11。表9与多元线性回归模型1参数估计基本一致。表11显示MAGE非线性部分检验有统计学意义，CAGE检验P值为0.06。

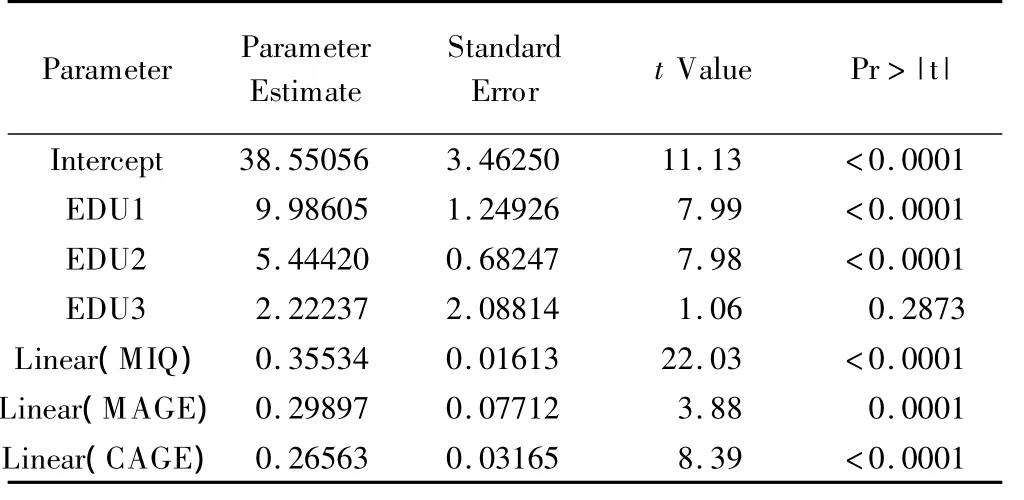
表9 GAM参化函数及非参数函数线性部分估计结果

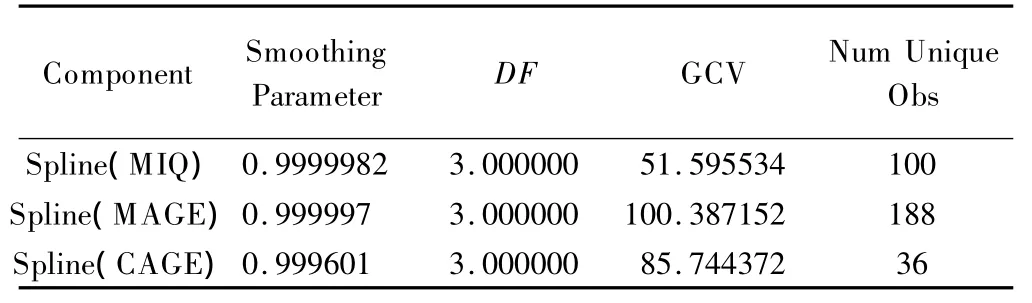
表10 GAM非参数函数非线性部分平滑拟合结果

表11 GAM非参数函数非线性部分假设检验结果

(2)程序及主要结果

PROC GAM DATA=IQSAMPLE;MODEL CIQ=PARAM(EDU1 EDU2 EDU3)SPLINE(MIQ)SPLINE(MAGE)SPLINE(CAGE)/METHOD=GCV DIST=GAUSSIAN;QUIT;

程序增加GCV语句，参数函数及非参数函数线性部分的拟合结果与程序(1)基本一致，非参数函数非线性部分的假设检验仍显示MAGE与IQ呈非线性相关，MIQ和CAGE的自由度远小于0，检验P值无法估计，提示MIQ和CAGE与IQ基本无非线性相关(表12)。

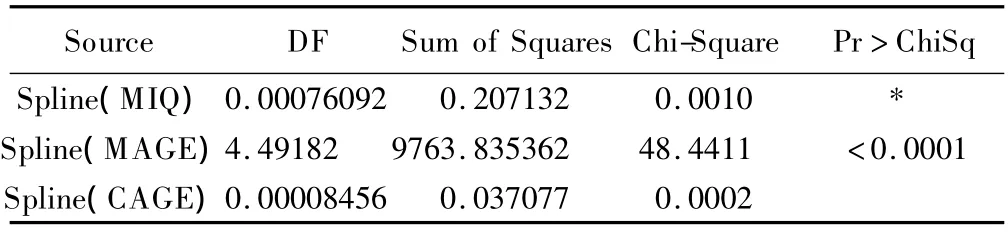
表12 广义交叉验证法假设检验结果

(3)程序及主要结果

ODS HTML;ODS GRAPHICS ON;PROC GAM DATA=IQSAMPLE;MODEL CIQ=PARAM(EDU1 EDU2 EDU3)SPLINE(MIQ)SPLINE(MAGE)SPLINE(CAGE)/METHOD=GCV IST=GAUSSIAN;QUIT;ODSGRAPHICSOFF;ODSHTML CLOSE;

程序输出了MAGE、CAGE和MIQ非参数函数非线性部分对IQ影响效应曲线(图2)。尽管CAGE和MIQ图像近似二次方曲线，但其效应值(纵坐标)远小于MAGE，自由度远小于0，检验P值无法估计，提示此类曲线无实际意义。MAGE曲线较为复杂，但母亲分娩年龄在22～35岁之间时，近似呈二次方曲线，而这部分人群占总人群的比例达91．5%，提示两侧曲线的稳定性弱。

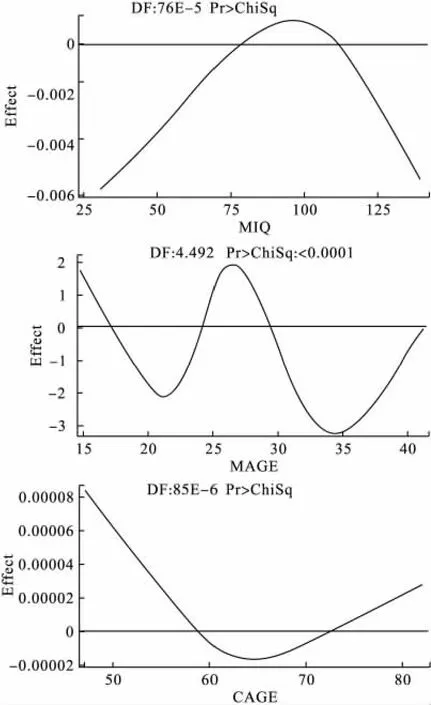
图2 GAM程序(3)部分输出结果

(4)程序及主要结果

ODS HTML;ODS GRAPHICS ON;PROC GAM DATA=IQSAMPLE;MODEL CIQ=PARAM(EDU1 EDU2 EDU3 MIQ CAGE)SPLINE(MAGE，DF=3)/DIST=GAUSSIAN;QUIT;ODS GRAPHICS OFF;ODS HTML CLOSE;

基于以上输出结果，对CAGE和MIQ按参数函数拟合，并限定 MAGE的总自由度为2和3，以简化MAGE非线性部分的效应曲线。简化后的图像均呈二次方曲线(图3)。

3．多元回归模型2的SAS程序及主要结果

PROC REG DATA=IQSAMPLE;MODEL CIQ=EDU1 EDU2 EDU3 MIQ CAGE MAGE MAGE_SQUARE;QUIT;

MAGE_SQUARE是新生成的变量，是MAGE的平方项。多元线性回归模型2的AIC值为19597.41，对IQSAMPLE预测的残差平方和为746762.65，对IQTEST预测的残差平方和为725704.04;参数估计结果见表13。模型2的AIC值以及对IQSAMPLE和IQTEST预测的残差平方和均小于模型1，提示模型2优于模型1。MAGE二次方项检验有统计学意义，回归系数符号所反映的开口方向与GAM输出的MAGE非线性部分效应曲线相吻合。

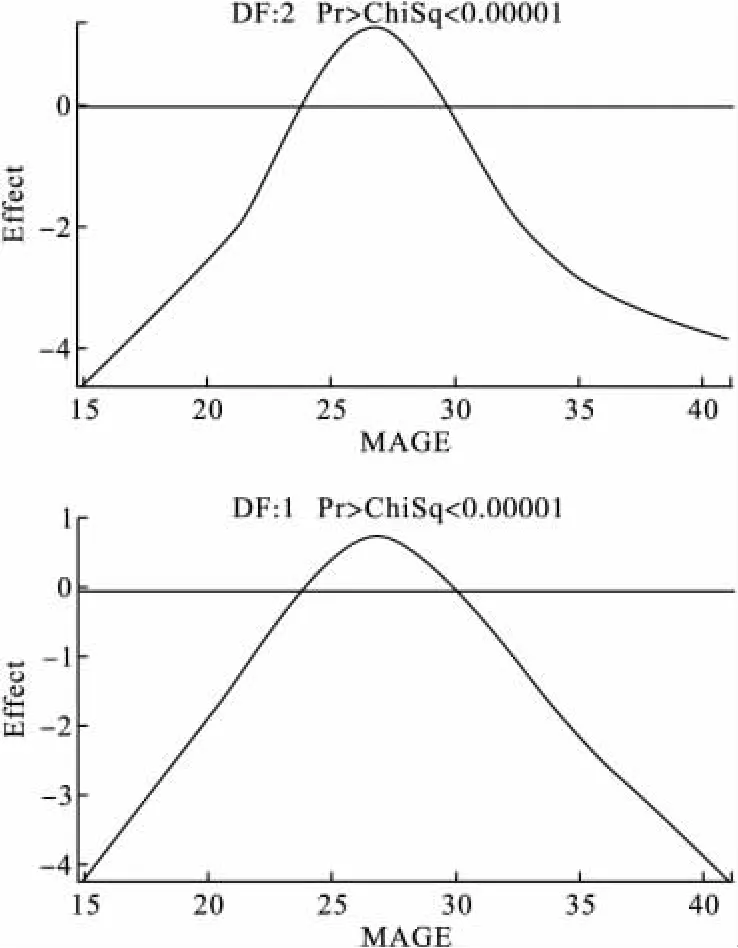
图3 GAM程序(4)的部分输出结果

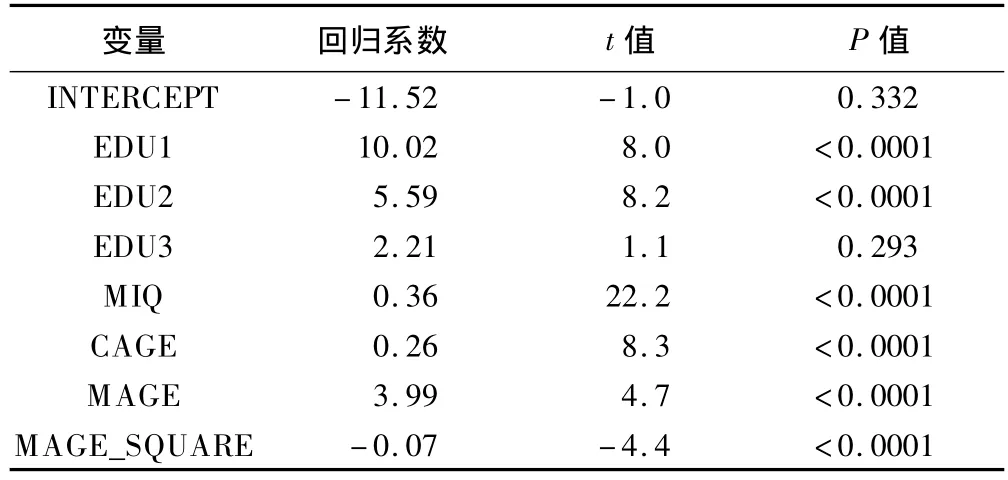
表13 多元线性回归模型2参数估计

讨 论

简要介绍了GAM有关知识及其SAS程序，通过实例数据说明了GAM识别变量间非线性相关对统计建模的重要性。强调了如何使用GAM识别变量间非线性相关，并将识别出的非线性相关引入经典的多元线性回归和logistic回归模型，进而对比评价了引入非线性成分和未引入线性成分的模型。GAM用于识别变量间非线性相关的特点是直观性好，以统计学检验为基础，可同时考察因变量与诸多自变量间的关系;合理使用GAM可改善多元线性回归和logistic回归模型的建模效果和预测精度。

1．Hastie T，Tibshirani R．Generalized additive models．Stat Sci，1986，1(3):297-318．

2．Hastie TJ，Tibshirani RJ．Generalized additive models．New York，NY:Chapman and Hall，Inc，1990．

3．SAS Institute Inc．SAS/STAT User's Guide，Version 9．2．Cary，NC:SAS Institute Inc，2008．

An Introduction of GAM in Identifying Non-linear Correlations and its Application in Statistical Modeling

Li Hongtian，Yuan Yue，Li Zhiwen，et al．Institute of Reproductive and Child Health/Ministry ofHealth Key Laboratory ofReproductive Health，Peking University Health Science Center(100191)，Beijing

ObjectiveTo introduce Generalized Additive Models(GAM)in identifying non-linear correlations and its application in statistical modeling for medical research data.MethodsA dataset was used for modeling with SAS PROC GAM．Goodness of fit and prediction precision were compared between models with and without non-linear components.ResultsA non-linear correlation could be identified by GAM．Compared with models without non-linear components，goodness of fit and prediction precision were improved by involving non-linear components.ConclusionModels with non-linear components reflect a true relationship between dependent and independent variables and hence improve the predictive ability．

Generalized additive models;Non-linear correlations;Statistical modeling