复杂孔隙结构储层渗透率评价方法研究

陈刚，潘保芝，王翠平，庄华

（吉林大学地球探测科学与技术学院，吉林长春130026）

复杂孔隙结构储层渗透率评价方法研究

陈刚，潘保芝，王翠平，庄华

（吉林大学地球探测科学与技术学院，吉林长春130026）

介绍核磁共振测井（NMR）在复杂孔隙结构储层评价中的应用。详细分析利用核磁共振的弛豫特性和扩散特性计算渗透率的模型优缺点。Coates模型和SDR模型比常规经验公式计算渗透率更准确，但大量岩心实验数据表明它们并不适用于特低渗透储层。提出一种新的定量评价物理函数——孔隙空间集中分布模型，它通过描述T2分布中可动流体体积分布的均一性，准确计算出低孔隙度低渗透率储层的渗透率。岩心数据计算表明，孔隙空间集中分布模型系数C与岩心渗透率具有很好的负相关关系，C值越小，表明孔径分布的集中程度越低，渗透性越好。岩心数据分析比较表明，该模型比经典核磁共振测井渗透率评价模型精度更高，对于定量描述复杂孔隙结构储层的渗透性具有很好适用性。

测井解释；核磁共振测井；孔隙结构；孔隙空间集中分布模型；渗透率；岩心分析

0 引 言

随着石油需求量的不断增加，迫切需要增加对低孔隙度低渗透率复杂储层勘探了解，核磁共振测井技术诞生以来，其独特优势给地质学家解决这类复杂储层的评价问题提供了全新思路［1］。常规测井确定地层渗透率误差较大，最大相对误差可达50%，而核磁共振测井计算渗透率相对误差小一个数量级［2］。这也提高了运用测井资料计算渗透率的精度。利用核磁共振测井的弛豫特性和扩散特性测量计算渗透率结果已经建立了很多经验关系式。但对于低渗透砂岩储层，尤其是特低渗透情况下，依据经典模型计算得到的渗透率与实验测量值相关性很差。本文针对上述情况提出一种基于T2分布集中程度的孔隙空间集中分布模型，可有效用于分析特低渗透砂岩储层的渗透性。

1 国内外的研究进展分析

岩石物理渗透率反映的是孔隙介质允许流体通过能力。渗透率与孔隙度及岩石比表面积有很好的相关性，可用Kozeny方程描述

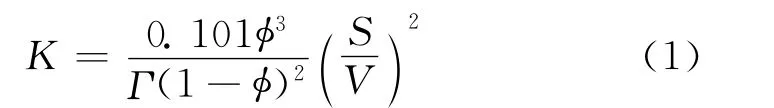
式中，K为渗透率，mD＊＊非法定计量单位，1mD＝9.87×10－4μm2，下同；S／V为岩石比表面积，cm2／cm3；φ为孔隙度，%；Γ是弯曲因子，无量纲，其值决定于单位长度内多孔固体中流体流过的路径以及孔隙的形状。

利用核磁共振弛豫特性和扩散特性建立不同模型计算渗透率，这些模型都是通过核磁共振实验、提出理论模型、通过研究其相互关系分析而得出的。

常规储层中常用的经典模型有2种：Coates模型和SDR模型［3］。

SDR模型

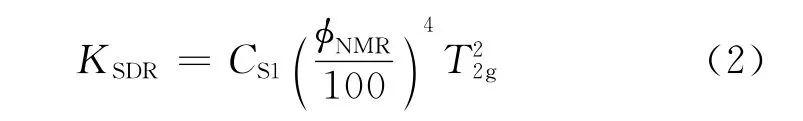
式中，CS1为模型参数；φNMR为饱和岩心样品核磁共振孔隙度；T2g为T2谱的几何平均值。该模型以平均弛豫时间为参数，受束缚水影响较小，不过对测量孔隙中流体的性质比较敏感，当岩石孔隙中含烃时，T2几何平均值会发生变化。

Coates－cutoff模型

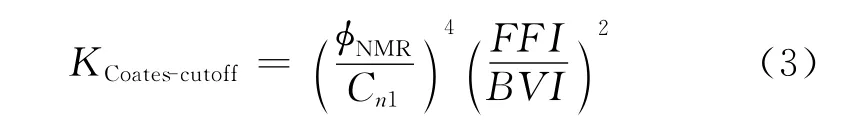
式中，Cn1为模型参数；BVI、FFI表示为由T2谱确定的束缚流体体积和自由流体体积。

Coates－sbvi模型

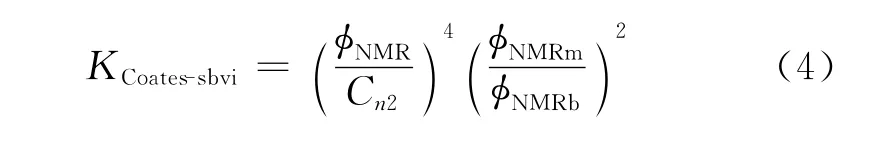
式中，Cn2为模型参数；φNMR为饱和岩心样品核磁共振孔隙度；φNMRm和φNMRb分别表示为由T2加权法求得的可动水体积和束缚水体积。在低孔隙度低渗透率砂岩储层情况下，李潮流等［4］通过物理场空间分布函数对低孔隙度低渗透率储层渗透率和孔隙结构做过探索研究，并且得到较好的应用结果。

2 NMR经典模型计算渗透率与常规方法对比

为了对比核磁共振测井经典模型计算渗透率与常规测井计算渗透率差别，分别采用2种方法计算渗透率。渗透率随束缚水饱和度增加而减小，随孔隙度的增加而增加，可以通过常规测井得到孔隙度和束缚水饱和度2个参数计算渗透率。渗透率与束缚水饱和度、孔隙度经验关系形式为

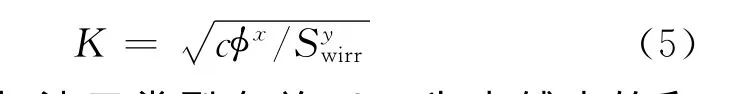
式中，系数c与油田类型有关；Swirr为束缚水饱和度；指数x及y主要与岩性有关。

分别利用式（3）和式（5）计算渗透率，计算结果如图1所示。图1中最右端一道K1为核磁共振测井Coates模型计算结果曲线，K2为常规经验公式计算曲线，蓝色为P型核磁共振测井仪器测量曲线。从图1中可以发现Coates模型计算结果与核磁共振测量渗透率值基本一致，相比之下由经验公式计算的渗透率值要偏大些。由常规经验公式计算的渗透率曲线变化趋势与MPHE曲线（指示总孔隙度）变化趋势基本相同。由图1（a）、图1（b）、图1（c）中3个不同渗透层可观察得出Coates模型计算渗透率比常规经验公式计算渗透率更准确。

但是在特低渗透碎屑岩储层情况下，Coates模型和SDR模型计算出的渗透率差别很大。具有相同孔隙度的岩石渗透率可以相差很大，关键是它们的孔隙结构差异，其中不同大小孔隙及其与喉道的相互搭配关系是影响渗流能力的主要因素［5］。因此，传统的经典模型并不能很好地表征特低渗透储层的渗透率。

图2为双对数坐标系下，Coates模型和SDR模型计算39块岩心样品得到的渗透率与岩心渗透率的关系，可以清楚地观察到这2个模型的相关性都很差，误差大约在1个数量级。其误差的主要原因是由于该地区储层孔渗条件都非常差，传统的经典渗透率模型主要是依据岩石孔隙宏观总体积刻画其渗透性，没有充分考虑孔隙的空间分布的联通性以及T2谱分布几何形态等信息。

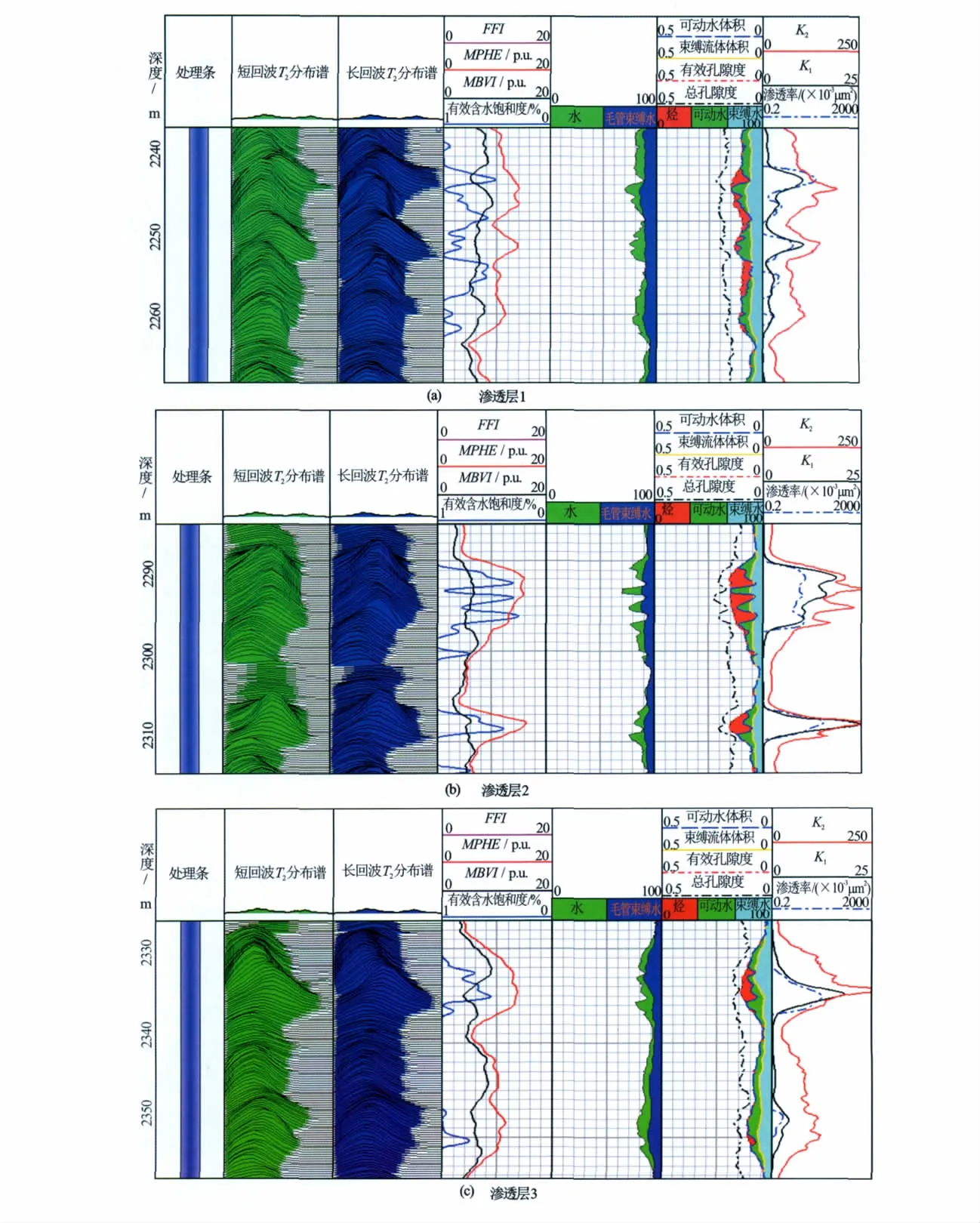
图1 Coates模型和经验公式计算渗透率结果

3 孔隙空间集中分布模型

在特低孔隙度渗透率砂岩储层渗透率研究时，必须充分考虑孔隙的空间分布联通性的影响，孔径大小及其分布特征对储层渗透率具有重要影响。因此利用核磁共振测井评价储层渗透率的关键是要充分考虑T2分布形态，着重研究不同大小孔隙的搭配关系［4］。为此，引入了一种新的定量评价物理函数，孔隙空间集中分布模型。

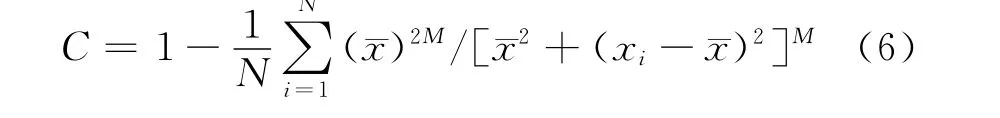
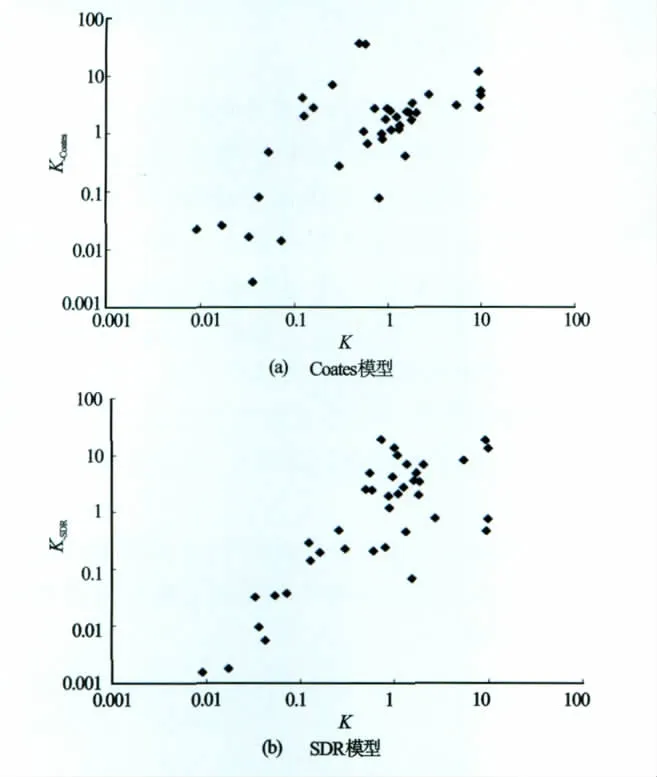
图2 由Coates模型和SDR模型计算出的渗透率与岩心渗透率交会图

式中，xi表示物理场分布的第i个分量；¯x为其均值；M为阶数。由式（6）可知函数C性质为：

（1）C值无量纲、归一化，0≤C＜1。

（2）C值越小，反映物理场的集中程度越小，物理性质分布越均匀，仅当C＝0集中程度最低，物理场的分布最均一，整个物理场的所有值xi都近似等于其均值［¯x］就是这种情况的特例；C＝1时集中程度最高，物理性质分布最不均匀，例如仅在一个空间点上不为0、其他点均为0就是这种情况的特例。

按照该模型，计算的C值越小，表明孔径分布的集中程度越低，整个岩石的孔隙尺寸大小空间分布越均一，渗透性越好；反之，C值越大，反映岩石孔隙尺寸大小空间分布越不均一，渗透率就相对越低。

为了验证该模型的适用性，选取了上述相同39块岩心样品进行核磁共振实验，其孔隙度分布范围为5.33%～14.98%、渗透率分布区间为（0.01～9.97）×10－3μm2。图3是由孔隙空间集中分布模型式（6）计算得到C值与渗透率的交会图。从图3中可以观察知，C值越小，渗透性越好；反之，C值越大，渗透率就相对越低。对比图3和图2可以发现，孔隙空间集中分布模型系数C与岩心渗透率具有很好的负相关关系。在半对数坐标系下，随着C值增加，渗透率呈数量级下降。当C＝0.36时，K＝ 9.97×10－3μm2；C＝0.798时，K＝0.01×10－3μm2。在特低孔隙度低渗透率情况时，依然具有很好的相关性，说明在特低渗透储层中，孔隙度相近时孔径空间分布特征是决定渗透率的关键因素。

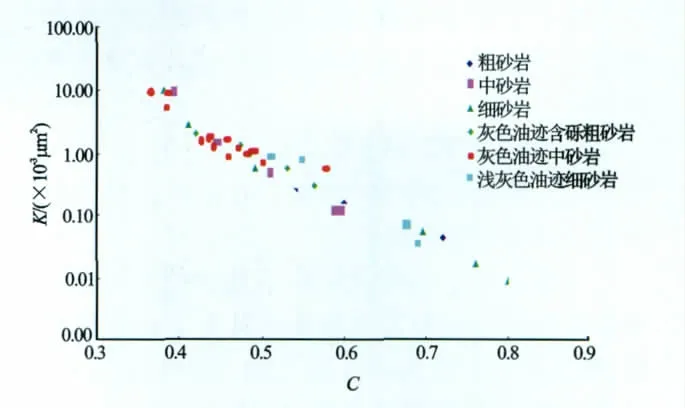
图3 孔隙空间集中分布模型C值与渗透率的交会图

图3中的渗透率相对较大者岩性主要是灰色油迹中砂岩、中砂岩和细砂岩，这几种砂岩的孔喉相对偏小，其渗流能力主要依靠那些相互连通的小孔隙。低孔隙度低渗透率储层情况下，中等或相对偏小尺寸的孔隙的分布及联通是此类储层存在一定渗流能力的关键因素，图3符合孔隙空间集中分布模型理论。当这些小孔隙尺寸大小越均匀，在整个空间场分布越均一，孔隙相互连通，渗透性就越好。

图4是渗透率、孔隙度和孔隙空间集中分布模型系数三者的三维立体网面图。

图4 渗透率、孔隙空间集中分布模型系数和孔隙度三者间三维立体网面图

为了便于观看，K轴为渗透率值取对数后乘以100，C轴取孔隙空间集中分布模型系数值的100倍，φ轴取孔隙度值的5倍。从图4中可以观察到当渗透率增高时，孔隙度增大，孔隙空间集中分布模型系数减小。图4表明，在不同的孔隙度渗透率条件下，利用上述模型计算的参数C与岩心渗透率和孔隙度都具有很好的相关性，说明这种基于T2分布集中程度的孔隙空间集中分布模型对于定量刻画特低孔隙度特低渗透率砂岩储层和常规砂岩储层的渗透性具有很好的适用性，较经典的核磁共振渗透率模型具有更高精度。

综上研究，这里提出一个在特低渗透复杂储层情况下，利用孔隙空间集中分布模型计算渗透率的新方法。

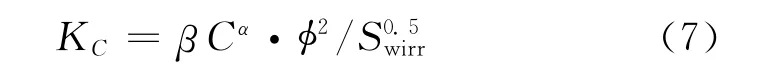
式中，KC是由孔隙空间集中分布模型计算的渗透率值；α、β为模型参数。

从图5可以清晰地发现，孔隙空间集中分布模型计算的渗透率与岩心渗透率具有非常好的相关性，相关系数为0.959 5。对比图2经典模型计算出的渗透率，充分体现了孔隙空间集中分布模型在计算渗透率方面的优越性。当然，孔隙空间集中分布模型计算的渗透率与岩心渗透率或多或少还是有些误差的，这些误差可能由孔隙空间泥质含量及其分布情况等因素所引起。

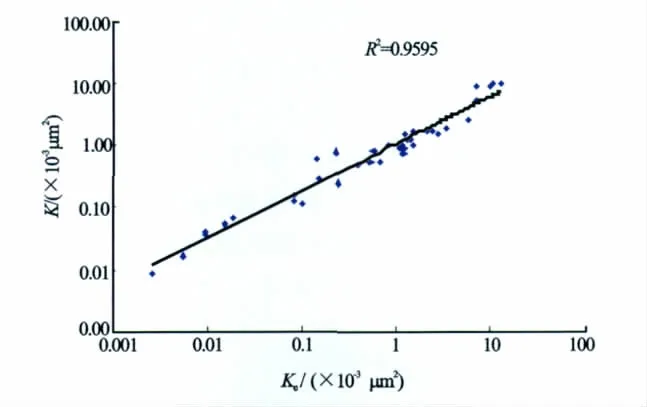
图5 孔隙空间集中分布模型计算渗透率与岩心渗透率交会图

4 结论与认识

（1）从该模型物理含义来看，计算的C值越小，表明孔径分布的集中程度越低，整个岩石的孔隙尺寸大小空间分布越均一，渗透性越好；反之，C值越大，表明孔径分布的集中程度越高，反映岩石孔隙尺寸大小空间分布不均一，渗透率就相对越低。

（2）孔隙空间集中分布模型可以定性地描述T2分布中可动孔隙体积分布的均一性，中等或相对较小尺寸的孔隙集中分布及其联通性是此类砂岩储层存在一定渗流能力的关键因素，通过该模型也证明了这一点。

（3）除此之外渗透率还受孔隙空间泥质含量及其分布以情况等因素所制约，可以运用多方资料进一步综合研究。

［1］ 肖立志.核磁共振成像测井与岩石核磁共振及其应用［M］.北京：科学出版社，1998：22－41.

［2］ 刘卫，肖忠祥，杨思玉，等.利用核磁共振（NMR）测井资料评价储层孔隙结构方法的对比研究［J］.石油地球物理勘探，2009，44（6）：773－778.

［3］ 熊鑫，哈达.核磁共振测井渗透率模型研究［J］.科技信息，2010，22：390－391.

［4］ 李潮流，徐秋贞，张振波.用核磁共振测井评价特低渗透砂岩储层渗透性新方法［J］.测井技术，2009，33（5）：436－439.

［5］ 付金华，石玉江.利用核磁测井精细评价低渗透砂岩气层［J］.天然气工业，2002，22（6）：39－42.

Permeability Evaluation Method for Complex Pore Structure Reservoir

CHEN Gang，PAN Baozhi，WANG Cuiping，ZHUANG Hua
（College of Geo－exploration Science and Technology，Jilin University，Changchun，Jilin 130026，China）

Introduced is the application of Nuclear Magnetic Resonance（NMR）logging in permeability evaluation of complex pore structure reservoir.Analyzed in detail are advantages and disadvantages of permeability calculation methods，with NMR relaxation property and diffusion property.Coates model and SDR model are more accurate in permeability calculation than conventional empirical formulas，but a large number of core experimental data show that they are not suitable for ultra－low permeability reservoir.Put forward is a new permeability quantitative evaluation method——pore space centralized distribution model，which could accurately calculate permeability of low porosity and low permeability reservoir by describing movable fluid volume distribution homogeneity in T2distribution.Core data calculation shows that factor Cin pore space centralized distribution model has well negative correlation with core permeability.Low factor Cvalue indicates low concentration of pore size distribution，and better permeability.Core data analyze and comparison manifest that the pore space centralized distribution model has higher accuracy and is suitable for permeability quantitative evaluation of reservoir with complex pore structure.

log interpretation，nuclear magnetic resonance（NMR）logging，pore structure，pore space centralized distribution model，permeability，core analysis

P631.84

A

2012－5－3 本文编辑 王小宁）

1004－1338（2012）04－0382－05

陈刚，男，1986年生，硕士研究生，从事测井解释评价方面的研究。