多级串联非比例阻尼隔震结构地震响应分析①

杜永峰，张尚荣，李 慧

（1．防震减灾研究所，兰州理工大学，甘肃 兰州 730050；2．西部土木工程防灾减灾教育部工程研究中心，兰州理工大学，甘肃 兰州 730050）

0 引言

由于隔震体系的隔震层与本体结构的阻尼性能有很大差异，结构整体呈现出非比例阻尼的特性。上个世纪50年代以来，国内外学者对非比例阻尼体系作了很多研究：Kelly［1］采用实振型分解法求解了双自由度基础隔震模型相对位移的近似小参数解；汪梦甫［2］采用虚拟激励法得到非比例阻尼线性体系随机地震响应计算的一般实数解析解答；周君求和彭跃社［3］采用矩阵摄动法得到非比例阻尼振动系统的近似解析解；笔者［4］采用分区瑞利阻尼模型，将实振型分解法应用于一般多自由度隔震结构体系的动力响应分析。

随着隔震技术的不断深入研究和快速发展，隔震层的位置已不再局限于基础顶面，本次修订的建筑抗震设计规范（GB50011－2010）［5］对隔震层位置也做了扩展，由“建筑物基础与上部结构之间”"改为“建筑物基础、底部或下部与上部结构之间”，这类层间隔震模式将整个隔震结构体系分成上部结构、隔震层、下部结构。若各子结构阻尼性能都不同，对于层间剪切型结构就构成了多级串联非比例阻尼模型，如图1所示。鉴于分区瑞利阻尼模型的物理意义直观，便于工程应用［6－7］，本文引用该模型并将这种阻尼矩阵表达形式推广至多级串联非比例阻尼模型，采用状态空间法对其进行地震响应分析。

图1 （GB50011－2010）隔震结构计算简化模型Fig．1 The simplified calculation model of（GB50011－2010）Isolated structure．

1 多级串联非比例阻尼隔震结构动力分析

1．1 多级串联非比例阻尼隔震结构运动方程

多级串联非比例阻尼体系在形式上仍与常见剪切型结构体系类似，其运动方程为

其中，［M］、［C］、［K］分别是系统的质量、阻尼、刚度矩阵；｛u｝、｛˙u｝、｛¨u｝分别是质点相对于地面的位移、速度、加速度向量；为地震地面加速度。

与一般常见结构不同的是阻尼矩阵［C］，具有多级串联非比例阻尼特性的结构。引用分区瑞利阻尼模型，将阻尼矩阵表达为

式中，［C0］代表瑞利阻尼矩阵；［Cr］为体现非比例阻尼的余项阻尼矩阵：

式中，al，bl，ai，bi，a，b分别是下部子结构、隔震层和上部子结构的瑞利阻尼比例系数，其值可由下式求得［6］：

式中，ξl、ξeq、ξ分别为下部子结构、隔震层和上部子结构的阻尼比。ω1和ωj分别为对系统动力响应有显著贡献的低阶和高阶圆频率。

式中，mj＋1和kj＋1分别是隔震层的质量和刚度；［Ml］和k1，k2，…kj分别是下部子结构的质量矩阵和层间刚度；［Mu］和kj＋2，…，kn分别是上部子结构的质量矩阵和层间刚度。

1．2 多级串联非比例阻尼隔震结构分析方法

为求解式（1）～（5）所表达的多级串联非比例阻尼隔震结构的动力响应，在状态空间法中，运动方程（1）可表示为

式中

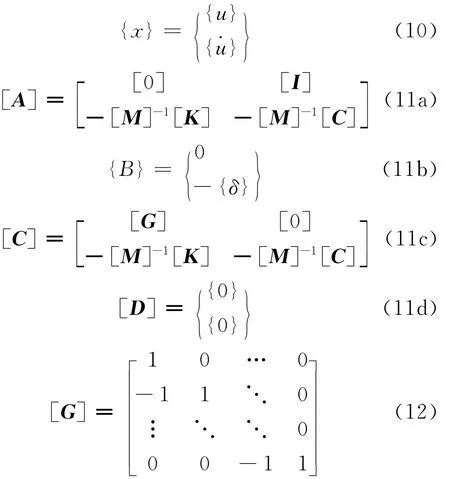
其中，｛δ｝＝［1 1…1］T；［I］为单位矩阵。根据需要给出表达式（8）、（9）中的各个分量，得出结构相对位移、速度或加速度响应。

2 算例分析

2．1 算例参数

算例1：选用笔者承担的一地下1层、地上10层钢筋混凝土框剪结构，结构参数如表1所示。隔震层位于地下室顶部，隔震参数如表2所示。

算例2：将算例1中结构形式改造为基础隔震结构，上部结构及隔震层参数与算例1相同，用作对比算例。

该建筑位于Ⅷ度（0．2g）设防烈度区，二类场地土，根据规范要求，选取符合场地要求的七条地震波，其中包括EI－Centro波、TAR＿TARZ波、Nor＿90＿w波、Taft021波、ANA＿00＿w波、兰州波、唐山波，计算结果取其最大平均值。

表1 结构参数（X向）

表2 隔震层刚度和质量（X向）

2．2 算例时程分析

（1）对算例1参数代入本文算法模型（8）～（12）进行时程分析，与采用MATLAB编制的 Wilson－θ法的结果进行对比；结果显示本文算法所得结构的位移、速度、加速度响应与Wilson－θ法结果一致，其中罕遇地震下结构地下室位移时程曲线如图2所示，其结果吻合较好，表明本文所用分析程序合理，可用于隔震结构弹性分析。

（2）隔震层参数相同时，分析结果如图3、4所示。算例1所得隔震层最大位移、最大层剪力比均大于相应的算例2的结果。这表明对带有地下室或大底盘之类的隔震结构，不能套用现有基础隔震体系的某些方法，若采用基础隔震模型进行动力分析，其结果存在误差。

图2 EI－centro波（400gal）作用下地下室位移时程曲线Fig．2 Displacement time－history curve of basement under EI－centro wave（400gal）．

为模拟算例1的动力分析结果趋近于算例2的动力分析结果，现假定算例1中地下室的刚度和质量同比例增大。在此假定下，比较分析结构响应随地下室刚度增加的变化趋势。整体结构最大层剪力比、隔震层最大位移随地下室刚度和质量的增加变化趋势分别如图5、图6所示。由于在本算例分析中的阻尼采用分区瑞利阻尼，而阻尼矩阵与刚度和质量相关，在分析过程中发现，当刚度增大20%以后层剪力比发散。考虑到一般结构阻尼变化很小，故在刚度增大20%时，保持阻尼矩阵不变，刚度和质量同比例增加，层剪力比系数与隔震层最大位移逐渐减小。当刚度和质量同时增大4～6倍时，层剪力比系数与隔震层最大位移趋近于算例2所得对应值，如表3、表4中刚度、质量增幅为400%、600%时的对应值所示。

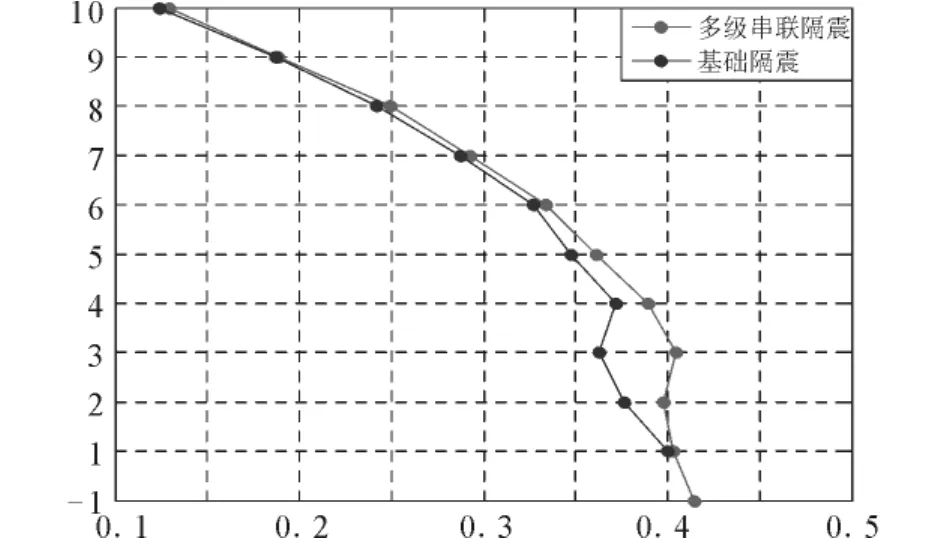
图3 多遇地震下最大平均层剪力比Fig．3 Maximum average layer shear ration under frequency earthquake．

图4 罕遇地震下最大平均位移 （m）Fig．4 Maximum average displacement under rear earthquake．

表3 基础隔震计算结果

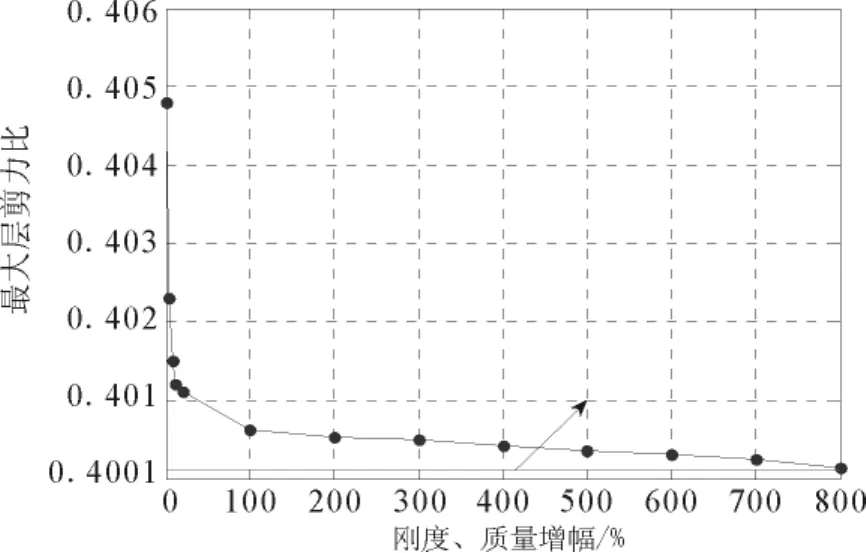
图5 最大层剪力比随地下室刚度、质量变化Fig．5 Maximum layer shear ration changes with the basement stiffness and quality．

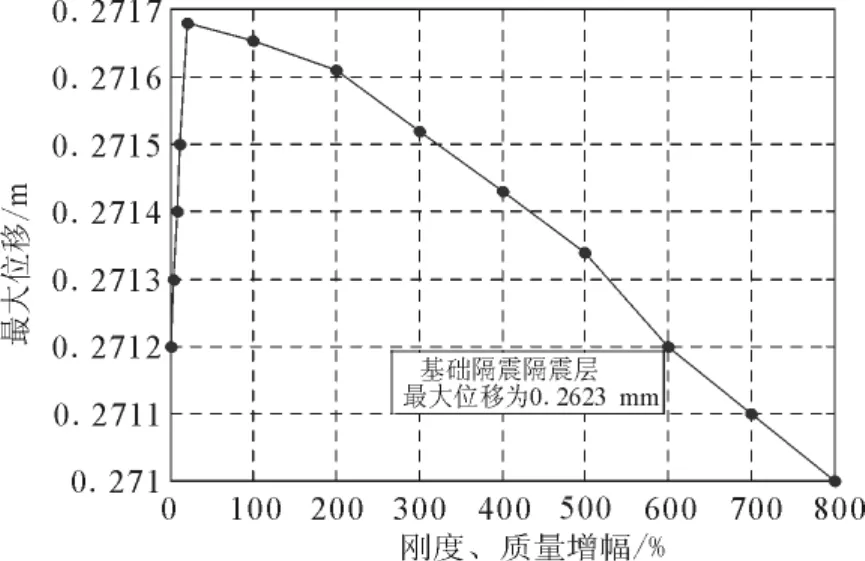
图6 隔震层最大位移随地下室刚度、质量变化Fig．6 Maximum displacement of isolation layer changes with the basement stiffness and quality．

表4 串联隔震结构响应随地下室刚度、质量增幅变化表

3 结论

本文对建筑抗震设计规范（GB50011－2010）修订的多级串联非比例阻尼隔震结构计算模型进行理论研究，并对其作了隔震性能分析，通过分析得出如下结论：

（1）本文推导的多级串联非比例阻尼矩阵物理意义明确。运用本文推导的阻尼矩阵进行动力分析较实用，对工程设计计算具有指导意义。

（2）随着下部结构刚度的增加，结构的层剪力和隔震层位移动力响应峰值均趋向于基础隔震结构的对应值，当下部结构为一层，且层间刚度大于上部结构底层层间刚度4～6倍时，可以近似按基础隔震结构进行动力分析。

［1］ J M Kelly．The role of damping in seismic isolation［J］．Earthquake Engineering and Structure Dynamic，1999，28（1）：3220－3221．

［2］ 汪梦甫．非比例阻尼线性体系平稳随机地震响应计算的虚拟激励法［J］．计算力学学报，2008，25（1）：94－99．

［3］ 周君求，彭跃社．求解弱非比例阻尼系统实模态解的阻尼矩阵摄动法［J］．动力学与控制学报，2008，6（5）：322－326．

［4］ 杜永峰，李慧，B F Spencer，等．非比例阻尼隔震结构地震响应的实振型分解法［J］．工程力学，2003，20（4）：24－32．

［5］ 中华人民共和国行业标准．GB50011－2010建筑抗震设计规范［S］．北京：中国建筑工业出版社，2010．

［6］ 杜永峰，赵国藩．隔震结构中非经典阻尼影响及最佳阻尼比分析［J］．地震工程与工程振动，2000，20（3）：100－108．

［7］ Yongfeng Du，Hui Li，Billie F，et al．Effect of non－proportional damping on seisimic isolation［J］．Journal of structural control，2002，9：205－236．

［8］ 周福霖．工程结构减震控制［M］．北京：地震出版社，1997．

［9］ 李春锋，杜永峰，李慧．阻尼连体结构地震响应影响参数研究［J］．西北地震学报，2012，34（1）：33－38．

［10］ Clough R W，Penzien J．Dynamics of structures 2nd ed［M］．New York：McGraw－Hill，1993．