自然电位测井数学模型与求解方法

李大潜蔡志杰陈娓谭永基王文娟王敬农

（1.复旦大学数学科学学院，上海200433；2.上海立信会计学院数学与信息学院，上海201620；3.中国石油集团测井有限公司技术中心，陕西西安710021）

在不同子区域的交界面（记为γk，k＝1，…，5）上，由电流的连续性，应满足交界面条件

自然电位测井数学模型与求解方法

李大潜1蔡志杰1陈娓2谭永基1王文娟1王敬农3

（1.复旦大学数学科学学院，上海200433；2.上海立信会计学院数学与信息学院，上海201620；3.中国石油集团测井有限公司技术中心，陕西西安710021）

编者按：李大潜先生，1937年生，复旦大学数学科学学院教授，中国科学院、发展中国家科学院及欧洲科学院院士，法国科学院及葡萄牙科学院外籍院士。曾为电阻率测井方法建立了统一的基本理论框架，据此制作的微球形聚焦测井仪器，20多年来一直成功地在大庆等多个油田使用。曾获国家自然科学奖二等奖、何梁何利基金科学与技术进步奖、华罗庚数学奖、上海市科技功臣奖、苏步青应用数学奖等科技奖励。谨以此文鼓励测井界广大同仁重视基础理论和基础方法研究。感谢李大潜院士对测井理论的突出贡献！

对石油勘探开发中常用的自然电位测井方法，在以往散见于各处的研究成果及近期研究的基础上，系统地总结了其相应的数学模型，并补充了众多算例，为自然电位测井在轴对称情况下建立了完整的理论框架。有关内容包括自然电位测井数学模型及其适定性，解的极限状态及相应的简化模型，有效求解的数值方法，并揭示了有关自然电位测井方法的算例及应用。

自然电位测井；轴对称情形；数学模型；数值方法

0 引 言

在石油勘探开发中，自然电位测井是最常见也是最重要的测井方法之一。由于电化学等因素的作用，地层中正负离子具有不同的迁移速度，且泥岩颗粒经常吸收正离子，因此在不同地层的交界面上会产生稳定的电位差，称为自然电位差，从而在地层中形成一个电场，为与人为供电产生的人工电场相区别，称其为自然电场。自然电场的分布和岩性有密切关系，特别是在砂／泥岩剖面中能以明显的曲线异常变化显示出渗透性地层。因此，通过研究井眼内自然电场中的电位变化即可反映井壁岩性，这种测井方法称为自然电位测井。自然电位测井具有方法简单、实用价值高等特点，是划分岩性和研究储集层性质、求取测井参数以及其他地质应用中不可缺少的基本方法之一［1－3］。

在进行自然电位测井时，得到的自然电位曲线（SP曲线）随着地层的改变而变化，可以指示渗透层的位置所在［4－8］。

1 自然电位测井的数学模型

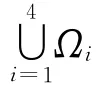
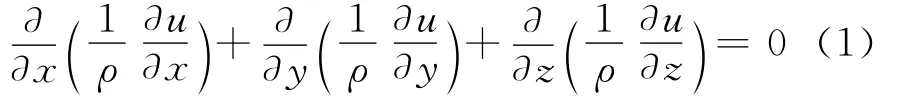
式中，ρ为地层电阻率，在各个子区域Ωi中，ρ＝ρi均为常数（i＝1，2，3，4）。记σ＝1／ρ为地层电导率，在各子区域Ωi中，σ＝σi＝1／ρi（i＝1，2，3，4）。本文总假设σi＞0（i＝1，2，3，4）。

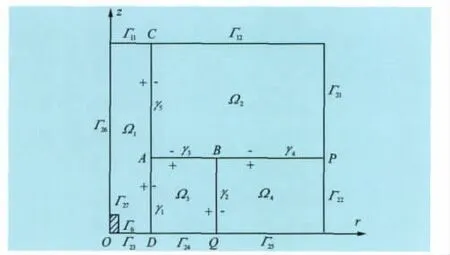
图1 地层剖面示意图

在轴对称假设下，方程（1）可改写为轴对称形式

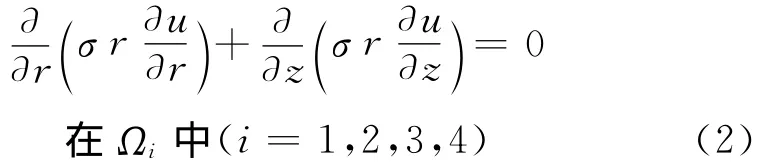
式中，n为Γ2的单位外法向量，而∂u／∂n为u的外法向导数。

注1 在实际应用中，电极被套在一有相当长度的绝缘套管上，此时Γ27应表示此绝缘套管之表面，而以下整个的讨论除特别说明外，均不受影响。

对于测量电极，它主要用来测量电极表面的电位值，而不发射电流。由于电极是良导体，其表面上的电位值应处处相等，为一个（待定）常数，于是在电极表面（记为Γ0）上应满足等位面边界条件［9］

在不同子区域的交界面（记为γk，k＝1，…，5）上，由电流的连续性，应满足交界面条件

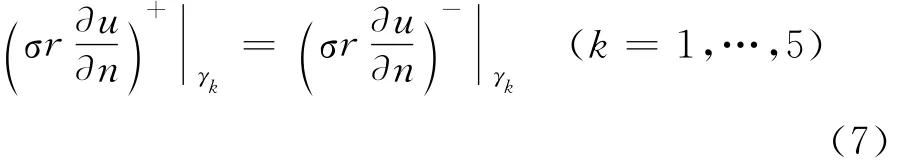
由于不同介质的交界面上存在自然电位差，因而

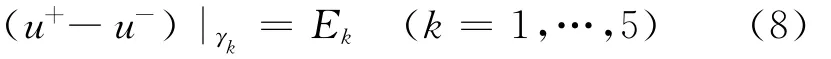
其中，Ek为交界面γk（k＝1，…，5）上的自然电位差，在应用中常设为常数，“＋”和“－”分别表示函数在交界面两侧的值，而在交界面上的单位法向量n规定对两侧有同一取向。

由与交界面条件（8）的相容性，电位函数u在地表面上Γ11部分应取常数

作变换

其中，u0为分块常数函数

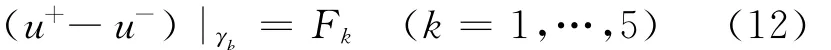
其中，

即在垂直交界面上不再存在自然电位差。因此，在Γ1＝Γ11∪Γ12上，边界条件（3）和（9）此时可统一地写为

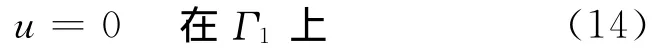
定理1.1 对任意给定的几何结构及地层电阻率，电极上、井轴上及区域Ω1和Ω2中的自然电位函数仅依赖于常数E5、E1＋E3和E1＋E2＋E4，而不是依赖于独立的5个常数Ek（k＝1，…，5）。

这一定理将会极大地减少制作相应测井解释图版的工作量。

这样，通过变换（10），就得到自然电位测井满足的数学模型：拟调和方程（2）满足相应的边界条件（14）、（4）～（6）及交界面条件（7）、（12）的边值问题。为后面叙述方便，将这一模型记为（SP）。

我们可以考虑（而且在下面的讨论中也要用到）更为一般的情形，即交界面上的自然电位差Ek（k＝1，…，5）可以不是常数，而是函数，记为Ek（s），其中，s是γk上分别以A（k＝1，3，5）和B（k＝2，4）为起点计算的长度，并假设Ek（s）是Hölder连续的。为保证交界面条件（8）与边界条件（4）的相容性，总假设

而为保证交界面条件（8）与边界条件（3）的相容性，边界条件（9）应取为

同样可将边界条件（3）和（16）统一地写为（14），且变换后相应得

在今后对自然电位测井的求解中，只会用到在A、B附近Ek为一般函数，而其余处Ek仍为常数的情形，此时式（15）自然满足。

2 自然电位测井数学模型的解的性质

2.1 解空间

为求解自然电位测井数学模型（SP），考虑等价的变分问题，为此先引进几个有关的函数集合。

对任意给定的p（1＜p＜∞），引入集合

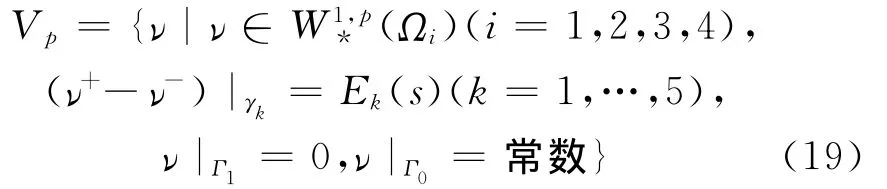
其范数定义为

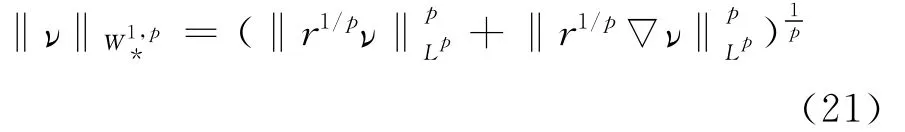
这样，与模型（SP）等价的变分问题为：求u∈Vp，使得其中，

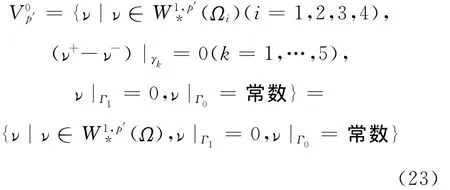
如果交界面上的自然电位差Ek（s）（k＝1，…，5）在交汇点A和B处的代数和分别为0，即满足

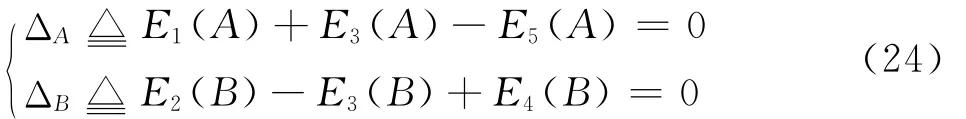
则称交界面上的自然电位差满足相容性条件［12］。此时，可在分块空间中求解上述问题（SP），并可用有限元素法求其数值解。

然而，通常交界面上的自然电位差并不满足相容性条件（24），此时整个电场中的电位函数具有一定的奇性，不再属于分块空间，从而不仅在理论分析上有本质困难，而且在数值计算时，不能直接用有限元素法求解。

下面先考虑解应隶属的空间［8，12］。从现在起，有关的引理及定理均只列出结论，而略去其证明。

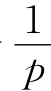
此处及以后，C（p）均表示一个仅依赖于p的正常数。

引理2.2 对任意给定的p（1＜p＜2），设Ek（s）∈Cα（γk）（k＝1，…，5），其中α＞1－，则Vp非空，且存在w∈Vp，使得

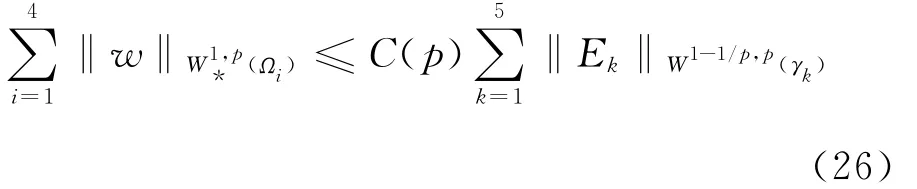
2.2 满足相容性条件时的分块解的存在性

设交界面上的自然电位差满足相容性条件（24），并记u是变分问题（22）在V2中的解。由引理2.1，V2非空，并任意取定w∈V2满足式（25）。记ν＝u－w∈，则对任意给定的φ∈，成立

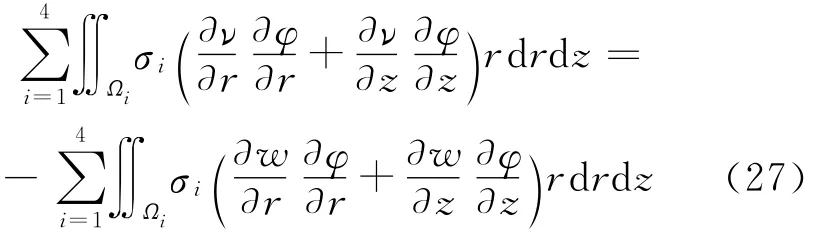
即

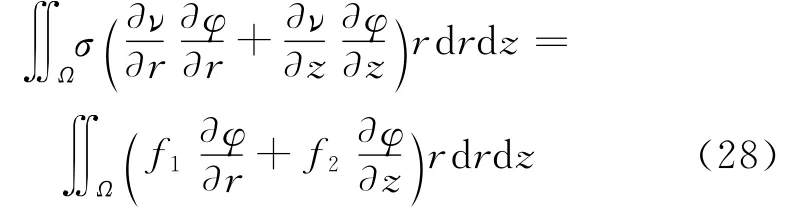
其中，在Ωi中，σ＝σi，f＝（f1，f2）＝σi▽w（i＝1，2，3，4）。显然，f∈［（Ω）］2。

由Lax－Milgram定理［13－14］，变分问题（28）在中存在唯一解ν∈，从而变分问题（22）存在唯一解u＝ν＋w∈V2。

如果相容性条件（24）不满足，由引理2.1，V2为空集，因而变分问题（22）不存在分块的解。而由引理2.2，对任意给定的p（1＜p＜2），Vp非空，从而可以考虑变分问题（22）的分块解的存在性。

2.3 不满足相容性条件时的分块解的存在唯

一性及估计［6，8］

定理2.1 存在ε0＞0，对于任意给定的p（2－ε0＜p＜2），问题（SP）存在唯一的解u∈Vp，且成立

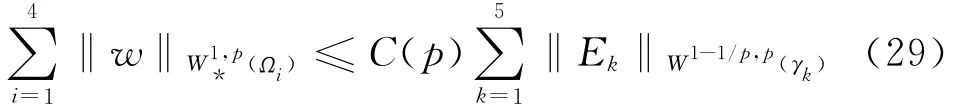
3 极限性态

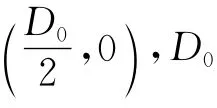
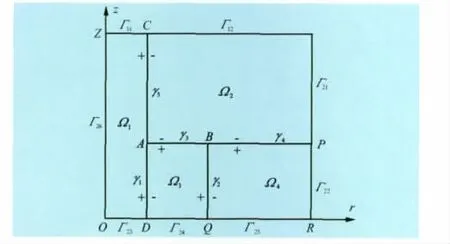
图2 椭圆型边值问题

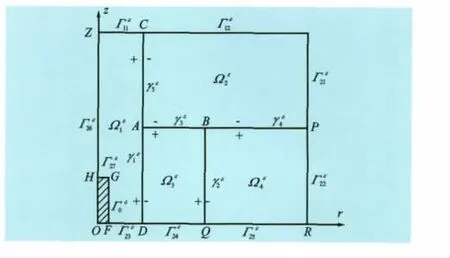
图3 等位面边值问题

及通常的边值问题（见图2）

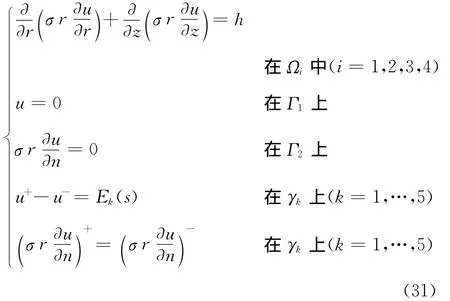
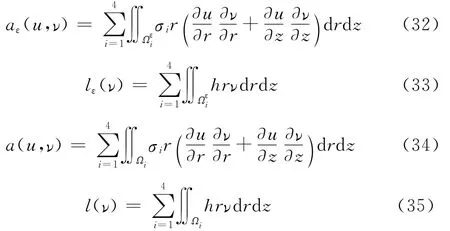
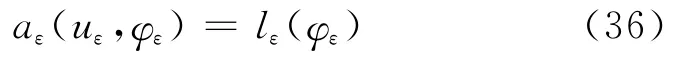
其中，

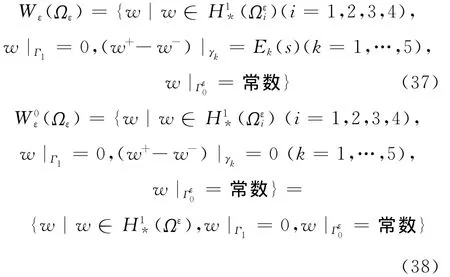
相应地，u∈W是下述变分问题的解：对任意给定的φ∈W0，成立

其中，

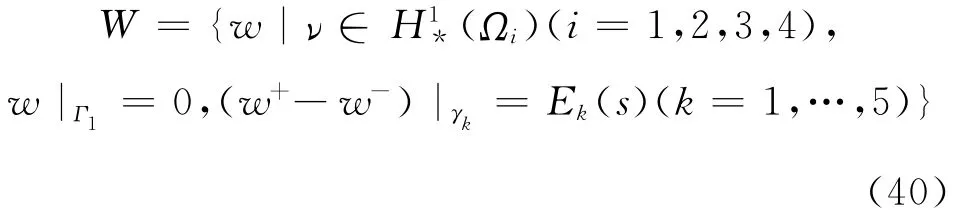
定理3.1 假设Ek（s）（k＝1，…，5）满足相容性条件（24）及E5（C）＝0。lε（ν）及l（ν）分别是ν在空间（Ωε）及W0上的线性连续泛函，则问题（30）和（31）存在唯一的分块解uε和u，且当ε→0（其中ε为电极的高度）时，

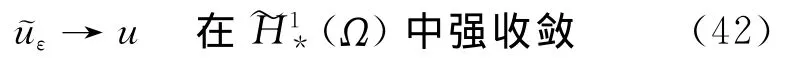
在实际应用中，交界面上的自然电位差Ek（k＝1，…，5）往往不满足相容性条件（24），由定理2.1，此时对任意给定的p（2－ε0＜p＜2），问题（30）和（31）存在唯一的分块解，而相应的等位面边界Γ0趋于原点时的极限性态则由如下定理给出。

定理3.2 当相容性条件（24）不满足时，存在ε0＞0，对任意给定的p（2－ε0＜p＜2），当电极的高度ε→0时

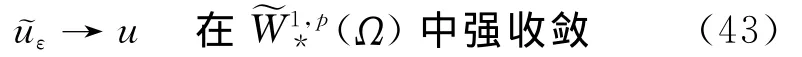
下面用数值模拟验证上述收敛性的结论。由于相容性条件（24）一般不满足，解存在奇性，不能直接使用有限元素法求解，需要采用一些方法去掉这一奇性。这里采用过渡带法（将在第4节中详细介绍），这是最为简便有效的方法。

取定以下基本几何参数：目的层的半层厚H＝2m，井筒半径R0＝0.125m，侵入带半径Rxo＝0.65 m，所考虑区域的径向深度R＝1 000m，纵向高度Z＝600m。选取4组不同的物理参数分别进行计算：

（1）ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶3∶4，E1＝10 mV，E2＝20mV，E3＝100mV，E4＝120mV，E5＝30mV；

（2）ρ1∶ρ2∶ρ3∶ρ4＝1∶10∶50∶100，E1＝10 mV，E2＝20mV，E3＝100mV，E4＝120mV，E5＝30mV；

（3）ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶3∶4，E1＝20mV，E2＝0mV，E3＝130mV，E4＝130mV，E5＝10mV；

（4）ρ1∶ρ2∶ρ3∶ρ4＝1∶10∶50∶100，E1＝20 mV，E2＝0mV，E3＝130mV，E4＝130mV，E5＝10mV。

固定测量电极的直径D0＝0.03m，将对应于不同电极高度ε（当ε→0时，原电极面退化为直径为D0的圆周）的相应问题在（D0／2，0）处的自然电位值（其中k＝1，2，3，4对应于上述4组不同物理参数取值情况，下同），并列出ε＝0（即无电极时）在（D0／2，0）处的自然电位值以及在原点处相应的自然电位值，计算结果见表1。

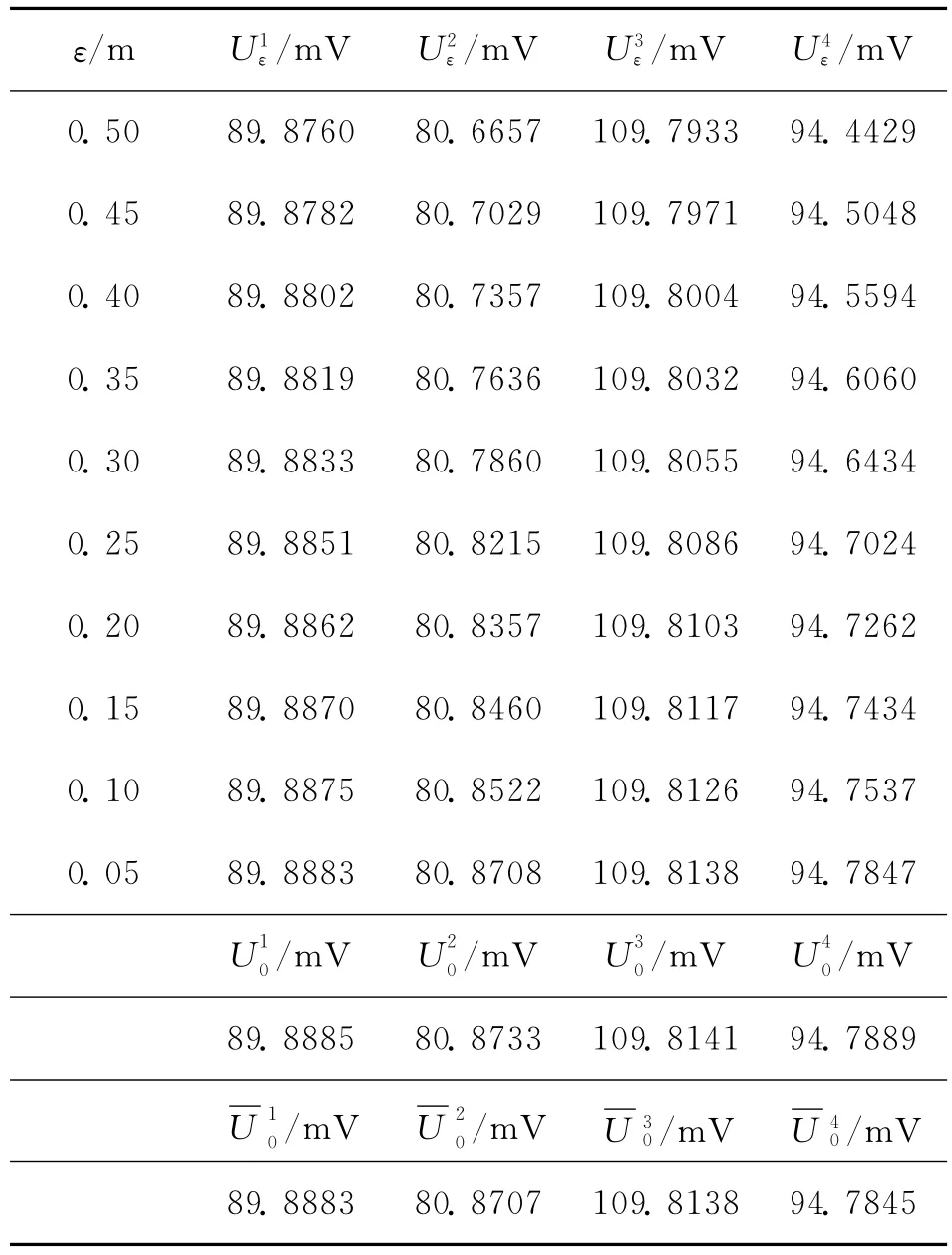
表1 电极高度的影响

现在同比例改变测量电极的高度ε和电极直径D的大小，将相应问题（在ε→0及D→0时，电极退化为原点）在（D／2，0）处的自然电位值记为（k＝1，2，3，4），并列出无电极时在原点处的自然电位值（k＝1，2，3，4），计算结果见表2。

4 求解方法

4.1 相容性条件（24）成立时的有限元素法

先考虑相容性条件（24）成立时，变分问题（22）的求解方法。由本文第2节，此时变分问题（22）存在唯一的分块解u∈V2。

不失一般性，对区域Ω作三角形剖分（为明确起见，这里我们假定对区域作三角形剖分，事实上，以下方法对其他形状的剖分也同样适用），则变分形式（22）可改写为

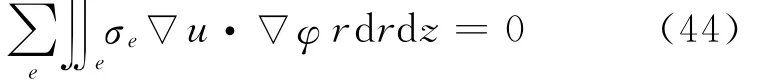
其中，e为任一三角形单元，且σe＝σi，若e⊆Ωi。

对任意给定的三角形单元e，记其3个顶点按逆时针顺序排列分别为（rp，zp）（p＝1，2，3），函数u在各顶点上的值为up（p＝1，2，3）。对函数u作线性插值

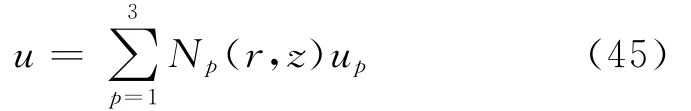
其中，

为形函数，其系数ap，bp，cp（p＝1，2，3）分别为

而

为单元e的面积。由此可以得到元素刚度阵

将元素刚度阵Ae组装成总刚度阵A，它是一个对称矩阵。

由于在交界面γk（k＝1，…，5）上存在自然电位差，需对其作相应的处理。为明确起见，规定仅保留上的电位函数值，而γ－k上的电位函数值需利用交界面条件（8）转化为用γ＋k上的电位函数值来表示的形式。

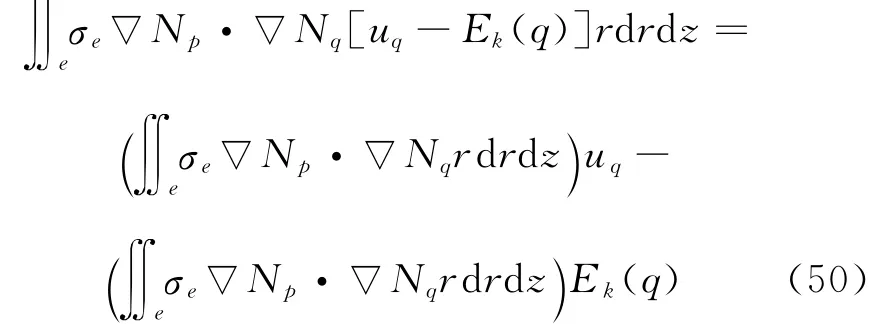
式（50）右端的前一项是对元素刚度阵的贡献，而后一项是对右端的贡献，可写为

其中，U＝（u1，…，uN）T为由电位函数在各节点的值构成的列向量（对于交界面γ上的节点，表示γ＋上的电位函数值），而N为节点总数。

对Dirichlet边界条件u｜Γ1＝0的一种处理方法是对系数矩阵A和右端项b作划行划列处理［9，16］：对Γ1上的任意一个节点k，将系数矩阵A的第k行和第k列划去，同时将右端项b的第k行（即第k个分量）划去。然而，这在计算机处理时需要对数据作大量的移动，会耗费较多的时间。

为了避免作这种数据移动，可采用另一种处理方法：对Γ1上的任意一个节点k，将系数矩阵A＝（apq）的第k行和第k列分别赋值为初始单位向量εk（即第k个分量为1，其余分量均为0的向量），即

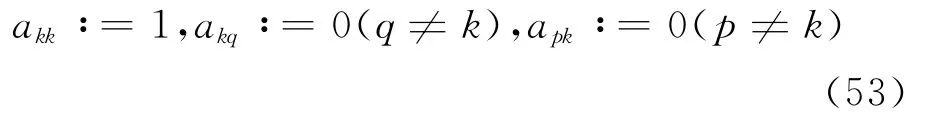
同时，将右端项b的第k个分量赋值为0∶bk＝0。

对等位面边界条件u｜Γ0＝常数作处理：固定Γ0上的一点，设其为节点k，对该等位面上的任意其他一个节点p，将系数矩阵A的第p行加到第k行，第p列加到第k列，然后再将第p行和第p列分别赋值为初始单位向量εp，即

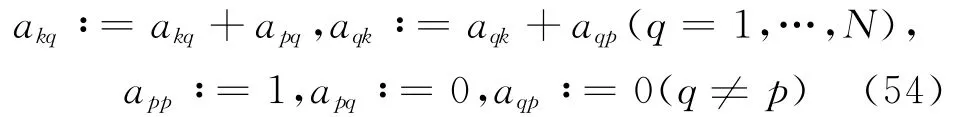
这样处理后仍保持矩阵A的对称性。

然后，将右端项b的第p个分量加到第k个分量，再令第p个分量为0，即

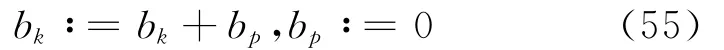
经过对边界条件的处理，得到线性代数方程组

4.2 相容性条件（24）不成立时的求解方法

如果相容性条件（24）不满足，由引理2.1，V2为空集，因而变分问题（22）不存在分块解。而由定理2.1，存在ε0＞0，对任意满足2－ε0＜p＜2的p值，存在唯一的分块解u∈Vp。

由于奇性的存在，不能直接使用有限元素法求解（22），需要采用一些方法去掉这一奇性。有3种可供使用的方法：过渡带法、移去奇性法和双层位势法。

4.2.1 过渡带法

过渡带法，又称为交界面条件相容化方法［5］。这是最为简便及有效的方法，特别值得推荐。对充分小的ε＞0，定义

其中，rA、rB分别为A、B的r坐标，

容易看出，这里只是将原有的交界面上的自然电位差Ek（s）（k＝1，…，5）在交汇点A及B的附近适当变化，使其满足相容性条件（24），从而由本文第2节，对应于（s）（k＝1，…，5）的问题存在唯一的分块解uε，且可用有限元素法进行求解。当ε充分小时，可以将uε作为原问题（22）的近似解。这一方法的合理性可由定理2.1保证，这就是定理4.1［8］。

定理4.1 存在ε0＞0，使对任意给定的p（2－ε0＜p＜2），过渡带法的解uε当ε→0时，在中强收敛于原问题的解u。

4.2.2 移去奇性法

在相容性条件（24）不满足的情形下，解决奇性的另一种方法是移去奇性法［6］，其基本思想：构造一个函数w，使得w在交界面上的跳跃值在A点和B点恰好满足

然后记ν＝u－w，将变分问题（22）改写为关于ν的形式，而ν满足相容性条件（24）。

下面介绍w的构造方法。

令

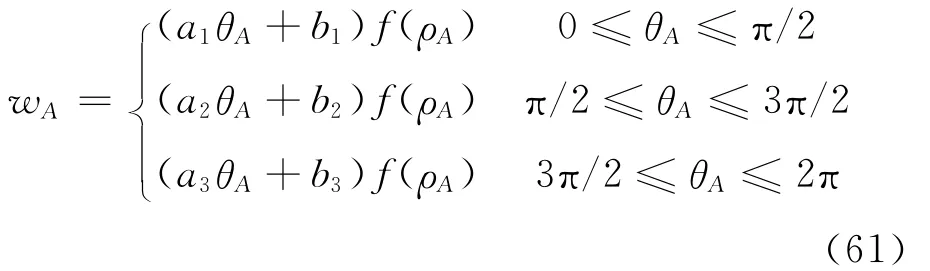
其中，

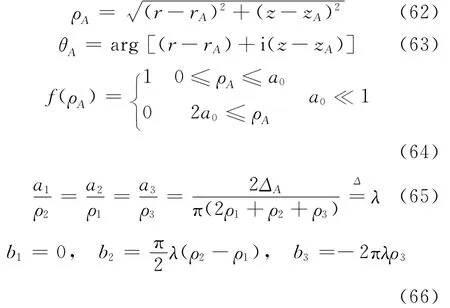
容易验证

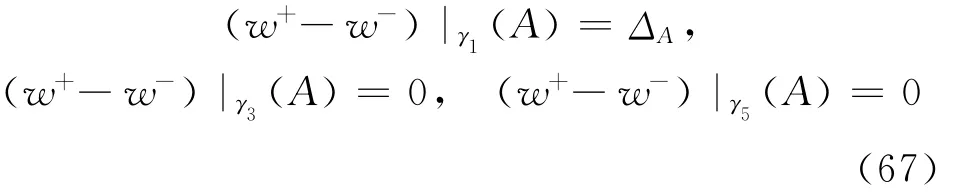
它满足式（59）。

类似地，适当选取

可使wB满足式（60）。

记ν＝u－wA－wB，将变分问题（22）改为ν的方程，而ν满足相容性条件（24），可用有限元素法求解。最后，由u＝ν＋wA＋wB得到原变分问题（22）的解。

4.2.3 双层位势法

第3种处理奇性的方法是双层位势法［17－18］。

在实际应用中，常设交界面上的自然电位差Ek（k＝1，…，5）为常数。由前述，利用变换（10），可将交界面条件变为

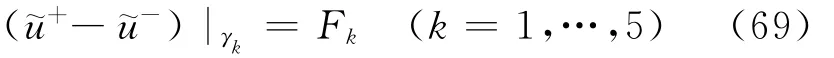
回到三维空间的地层模型来考虑问题。若介质在整个地层中是均匀的，由双层位势的定义［19－20］，具单位偶极矩面密度的偶极子双层面Σ对空间中任一点M所产生的电位为

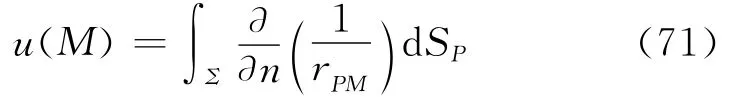
其中，rPM是点M到Σ上某一点P的距离；dSP为双层面Σ上的面积微元；n为负电荷所在面Σ—指向正电荷所在面Σ＋的单位法向量（见图4）。

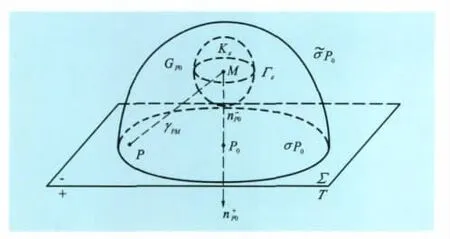
图4 双层位势法

双层位势（71）具有如下的性质［19－20］：

引理4.1 对任意给定的M∉Σ，双层位势（71）在M点处是调和的，即

引理4.2 双层位势（71）在Σ上具有第1类间断，且对任意给定的P0∈Σ，有

引理4.3 对任意给定的P0∈Σ，双层位势（71）的外法向导数在P0点是连续的，即

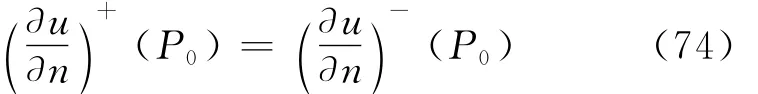
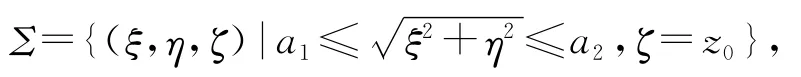
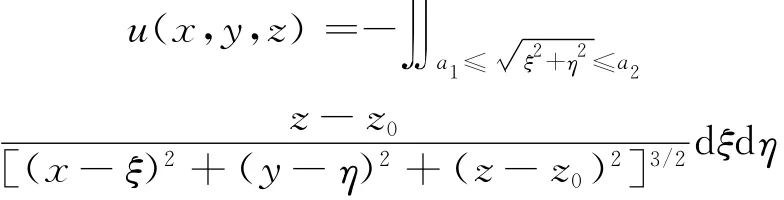
作极坐标变换

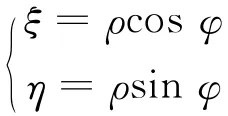
易见有

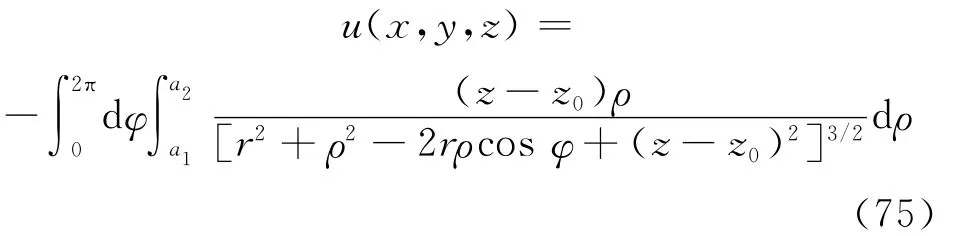
定理4.2 设

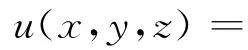
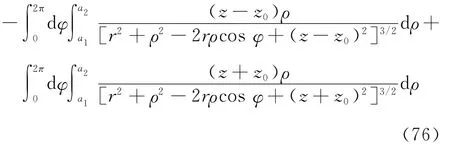
则有

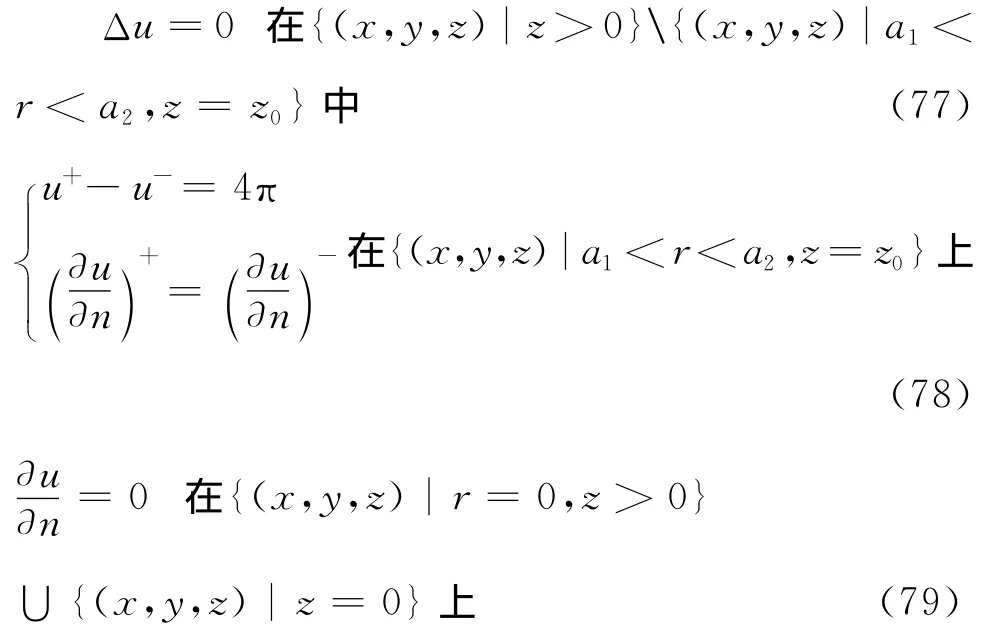
且有估计式

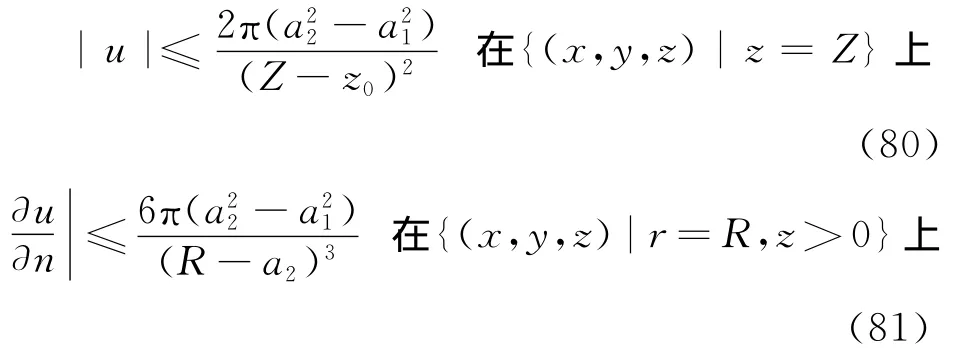
其中，R＞a2，Z＞z0。

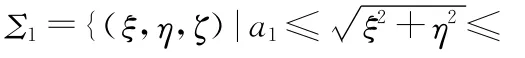
现在利用前述双层位势的性质，寻求问题（22）的数值解。在这里能够得到简便处理的，是应用中在交界面上具常数自然电位差的情形，而且只针对测量电极尺寸较小、可以近似为对称轴上一点的情形（见本文第3节）。此时的计算框架如下：

第1步 利用双层位势的性质，找到满足方程（2）及交界面跳跃条件w＋－w－＝Fk（k＝1，…，5）的函数w，其中F1＝F2＝F5＝0，而F3、F4由条件（70）式确定。

第2步 作平移ν＝˜u－w，此时ν仍满足原方程（2），但在交界面上连续，于是可利用相应的变分问题，藉助于有限元素法求解。

第3步 令u＝u0＋w＋ν，即可求得原问题（22）的解。

根据上述计算框架，可给出具体的实施细节及有关公式［17，18］。

5 数值模拟

5.1 均匀地层

设整个地层中介质是均匀的，即ρi＝ρj（i≠j）；又设自然电位差E4和E5一直延伸到无穷远处。此时，井轴上自然电位的精确解表达式［4，7］为

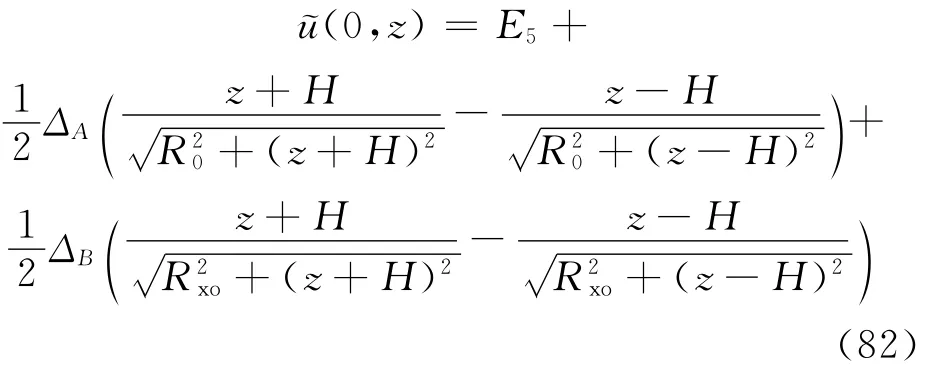
取H＝2m，R0＝0.125m，Rxo＝0.65m，E1＝10mV，E2＝20mV，E3＝100mV，E4＝120mV，E5＝30mV，R＝1 000m，Z＝600m。将电极A0近似为井轴上的原点，分别利用过渡带法和双层位势法在近20 000个节点的网格剖分下做数值计算，同时利用式（82）计算井轴上的自然电位精确值。比较发现它们在井轴上的值误差很小（见图5）。再取E1＝20mV，E2＝50mV，E3＝130mV，E4＝140mV，E5＝30mV，其余参数不变，它们的结果亦非常接近（见图6）。

图5 均匀地层情形1

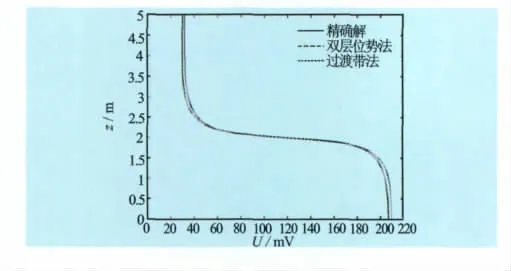
图6 均匀地层情形2

5.2 非均匀地层

自然电位测井的主要目的之一是判定地层，也就是识别各地层的交界面。取H＝2m，R0＝0.125 m，Rxo＝0.65m，E1＝10mV，E2＝20mV，E3＝100 mV，E4＝120mV，E5＝30mV，R＝1 000m，Z＝600m。考虑下面2种非均匀情形：

ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶2∶2

ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶3∶4

用双层位势法（设电极已按本文第3节中所述收缩为对称轴上的1个点）绘出井轴上的SP测井曲线（见图7及图8中的点虚线）；同时用过渡带法计算井轴上的SP测井曲线（见图7及图8中的实线）。从图7及图8中清楚地看到2种方法的计算结果很接近。

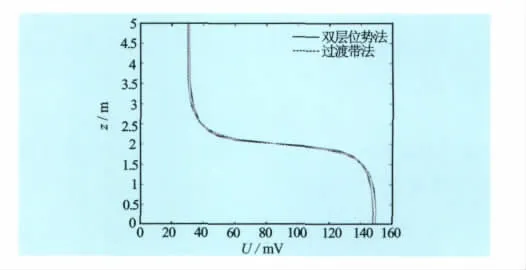
图7 非均匀地层ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶2∶2

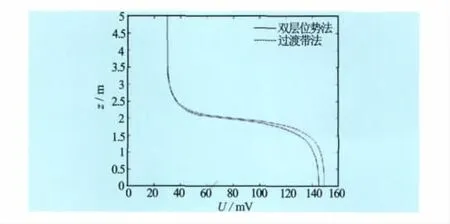
图8 非均匀地层ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶3∶4

5.3 在交界面交汇点A附近自然电位及电场

固定物理参数ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶3∶4，E2＝20mV，E3＝100mV，E4＝120mV，E5＝30 mV，选取2组不同的E1值分别进行计算，绘制A点附近的等位线图和电场图。

（1）E1＝10mV；（2）E1＝200mV。

对此2种情形，均成立ΔB≜E4－E3－E2＝0，即在交界面交汇点B处满足相容性条件，而ΔA≜E3－E1－E5≠0，故重点考虑在A点附近的情况。

图9及图11显示2种情形下在A点附近的自然电位情况。由于交界面上电位有跳跃，我们在A点附近的3块区域（Ω1、Ω2、Ω3）上分片绘制等位线，图形显示A点附近电位的变化比较剧烈。

图9 情形1时的等位线图

图10 情形1时的电场分布图

图10及图12显示2种情形下在A点附近的电场情况。由于各点电场强度之值不同，且在离交界面近的地方电场强度值显著趋大，为了观察电场的走向，图10及图12中各点的电场矢量均做了单位化处理。

我们观察到在2种情形下A点附近的电场旋转方向正好相反（情形1为逆时针，情形2为顺时针）。注意到情形1下ΔAE3－E1－E5＝60＞0；而情形2下ΔA＝－130＜0。二者不同的符号决定了2种不同的电场走向：当ΔA为正时，A点附近的电场按逆时针旋转；而当ΔA为负时，则按顺时针旋转。从其他类似的算例也可以看到这一点。

5.4 ρ1很大时套管壁上自然电位曲线

取定ρ1∶ρ2∶ρ3∶ρ4＝5000∶2∶3∶4，其中电阻率ρ1相对取值很大，可以近似地将井筒区域Ω1视为绝缘。分别取下面2组不同的自然电位差参数：

（1）E1＝10mV，E2＝20mV，E3＝100mV，E4＝120mV，E5＝30mV；

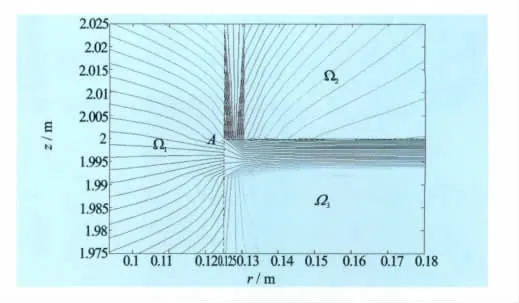
图11 情形2时的等位线图

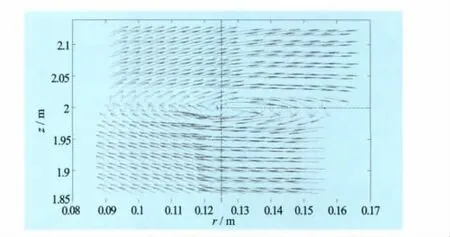
图12 情形2时的电场分布图

（2）E1＝20mV，E2＝0mV，E3＝130mV，E4＝130mV，E5＝10mV。

它们均满足B点的相容性条件ΔB≜E4－E3－E2＝0，而在A点ΔA≜E3－E1－E5≠0。

图13及图14显示对这2种情形套管壁（r＝D／2）上的自然电位曲线。从图中可以观察到在该曲线拐点处（它相应于目的层与围岩的分界处）自然电位值的跨度与相应的ΔA值一致：在情形1时，ΔA＝60mV，而在曲线拐点附近自然电位的最大值为90mV，最小值为30mV；而在情形2时，ΔA＝100 mV，而曲线拐点附近自然电位的最大值为110 mV，最小值为10mV。这一事实与物理上的直观结论吻合。

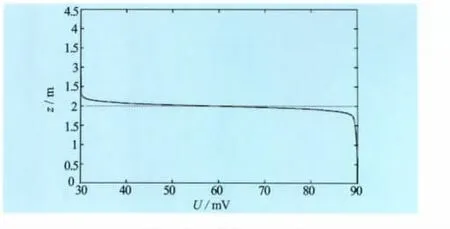
图13 套管壁自然电位曲线（情形1）

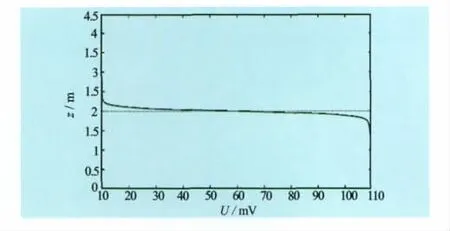
图14 套管壁自然电位曲线（情形2）

5.5 参数对自然电位曲线的影响

测井仪器工作时，其测井响应不可能正好反映目的层的电参数信息。实际上，测井响应将在不同程度上受到井筒、侵入带和上下围岩的影响。因此，测井的电阻率响应称为视电阻率，它与目的层的真电阻率是有差别的。为了让测井视电阻率响应尽可能地接近目的层真电阻率，要求对测井响应作出校正和正确的反演、解释，这就需要对大量的地层模型测井响应数据进行比较研究。

影响自然电位测井响应的因素多种多样，可分别对不同的地层厚度、井筒半径、侵入带半径、围岩电阻率、侵入带电阻率及目的层电阻率进行相应的数值模拟，评估各因素对测井响应的影响。

例如，可取自然电位差参数为E1＝20mV，E2＝0mV，E3＝130mV，E4＝130mV，E5＝10mV，所考察的地层尺寸为R＝1 000m，Z＝600m。此外，设定H＝2m，R0＝0.125m，Rxo＝0.65m，ρ1∶ρ2∶ρ3∶ρ4＝1∶10∶50∶100为基本参考参数值，可通过数值试验每次只考虑测井响应随其中一种参数变化的情况，其余的参数则取这组数据中相应的值。具体计算结果从略。

6 将自然电位测井仪安装在侧向测井仪上对自然电位测井的影响

在实际测井中，常将自然电位测井与侧向测井联合使用，并将自然电位测井仪安装在侧向测井仪的上方（见图15）。其中A为自然电位测量电极环，直径为30mm，长度为250mm；B为一段绝缘表面的电缆，可视为绝缘体，直径为30mm，长度为4.5 m；C为导体，直径为90mm，长度有3种情况：5、10、15m；D为绝缘体，直径为90mm，长度为800 mm；E为双侧向仪器＋声波仪器，直径为90mm，长度信息见图16。

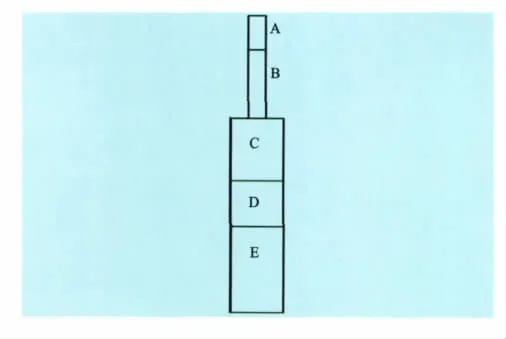
图15 自然电位测井仪安装在侧向测井仪的上方

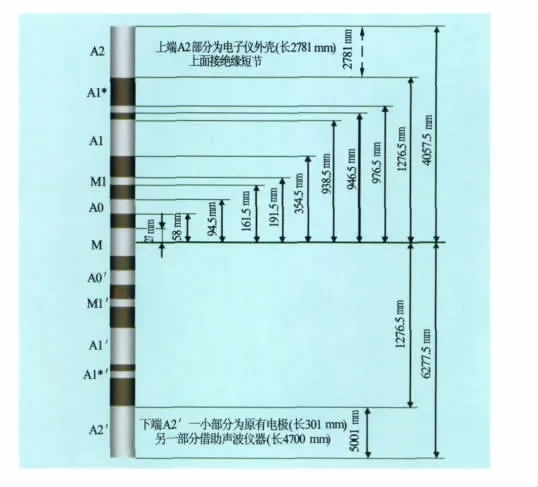
图16 侧向测井仪器数据

在进行侧向测井时，自然电位测井仪不工作；而在进行自然电位测井时，侧向测井仪不工作。由于侧向测井仪由众多大小不同的电极组成（包括1个发射电极，若干屏蔽电极及测量电极），而且为隔开这2类测井仪器，在其间还插有圆柱形的导体C（相当于一个不发射电流的电极）及圆柱形绝缘电缆B及D。在进行自然电位测井时，尽管这些电极处于不工作的状态，即它们不发射电流，但由于它们及绝缘体的存在，原先自然电位场所在区域被它们在井轴附近占据了一部分，原先的一部分本质上满足绝缘条件的井轴，要代之以这些电极Γk（k＝1，…，l）表面上的齐次等位面边界条件

这样，原先求解自然电位的等位面边值问题（1）～（9）要代之以等位面边值问题（1）～（9）及（83）～（85），它们具有不同的求解区域及一些不同的边界条件，整个自然电位场要相应地发生变化。特别地，在测量电极Γ0上的自然电位值U（这是自然电位测井主要关心的对象）要相应地发生变化。一个迫切需要考虑的问题是：这样做对测量电极上的自然电位值U会不会带来重大的影响。

为了检验侧向测井仪器的电极串对自然电位测井的影响，针对图16所示的数据，我们取半层厚H＝2m，井筒半径R0＝0.125m，侵入带半径Rx0＝0.65m，并对所考虑区域取径向深度R＝1 000m及纵向高度Z＝600m，通过过渡带法进行数值计算。记未加入侧向仪器电极串时测量电极Γ0上的自然电位值为U，加入侧向测井仪器电极串时相应的电位值为˜U，取下面的几组数据进行计算，计算结果见表3。

（1）ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶3∶4，E1＝10mV，E2＝20mV，E3＝100mV，E4＝120mV， E5＝30mV；

（2）ρ1∶ρ2∶ρ3∶ρ4＝1∶10∶50∶100，E1＝10mV，E2＝20mV，E3＝100mV，E4＝120mV，E5＝30mV；

（3）ρ1∶ρ2∶ρ3∶ρ4＝1∶2∶3∶4，E1＝20mV，E2＝50mV，E3＝130mV，E4＝140mV，E5＝10mV；

（4）ρ1∶ρ2∶ρ3∶ρ4＝1∶10∶50∶100，E1＝20 mV，E2＝50mV，E3＝130mV，E4＝140mV，E5＝10mV。

对LC的长度分别为5、10m及15m时分别进行计算，结果表明加入侧向测井仪器电极串后对自然电位测井的影响很小。

下面我们再重点考察隔开2组电极系、具绝缘表面的电缆B的长度LB大小对测量自然电位值U的影响。取E1＝10mV，E2＝20mV，E3＝100mV，E4＝120mV，E5＝30mV，ρ1∶ρ2∶ρ3∶ρ4＝1∶10∶50∶100进行考虑，见表4。此种情况下，未加入侧向测井仪器电极串时测量自然电位值U为126.5869mV。

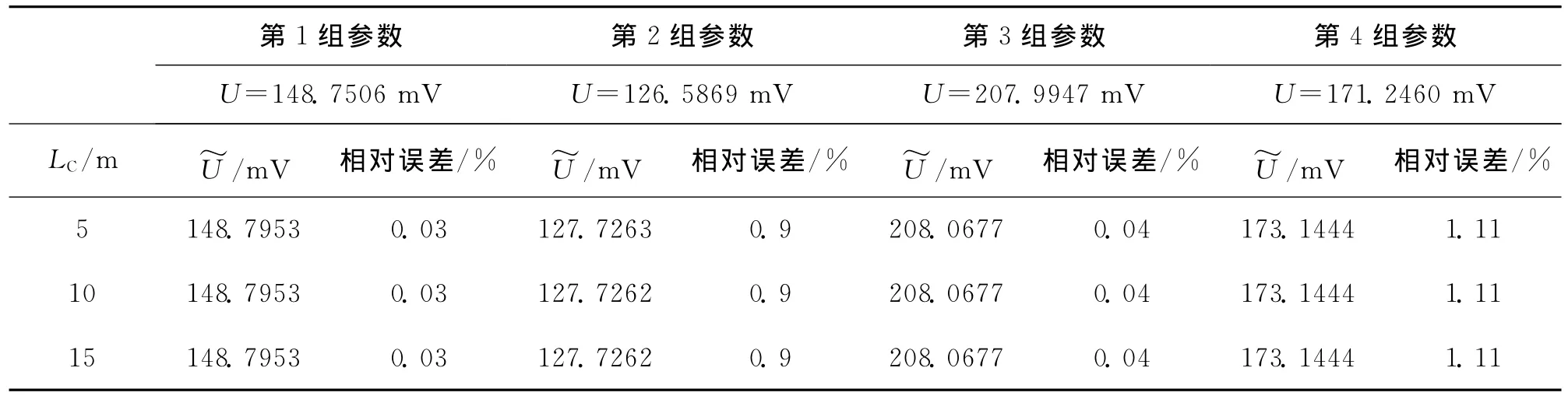
表3 计算结果

表4 电缆B的长度LB大小对测量自然电位值U的影响

由此可见，绝缘电缆B的长度LB不能太长，特别是不能太短，否则将（可能严重）影响自然电位测井的结果。现有仪器设计中取LB的长度为4.5m，值的相对误差（－U）／U约为0.9%，符合工程需要。而LB的长度最好选择为6m或者说6.5m，其相对误差分别为0.18%及0.27%。

7 结 论

（1）建立了自然电位测井的数学模型，并在交界面上的自然电位差满足相容性条件的特殊情况及不满足相容性条件的一般情况，分别在不同的函数空间中，揭示了该模型在数学上的适定性。

（2）在电极的尺度很小时，讨论了自然电位测井问题的解的极限性态，并据此对该数学模型作了适当的简化。

（3）对交界面上的自然电位差满足相容性条件及不满足相容性条件的2种情况，分别提出了如何有效地利用有限元素法求解自然电位测井问题的数值方法。

（4）根据实际的需要，提供了众多的算例，验证了前述的理论，并对有关的应用提供了指导。

［1］ 张庚骥.电法测井［M］.东营：中国石油大学出版社，1996.

［2］ 楚泽涵，黄隆基，高杰，肖立志.地球物理测井方法与原理：上册［M］.北京：石油工业出版社，2007.

［3］ 潘和平，马火林，蔡柏林，牛一雄，等.地球物理测井与井中物探［M］.北京：科学出版社，2009.

［4］ 彭跃军.自然电位测井中的数学方法［J］.应用数学与计算数学学报，1988，2（2）：35－43.

［5］ Li Tatsien，Tan Yongji，Peng Yuejun，et al.Mathematical Methods for the SP Well－Logging［M］.Applied and Industrial Mathematics，Venice－1（edited by R.Spigler），Kluwer Academic Publishers，1991，343－349.

［6］ Li Tatsien，Tan Yongji，Peng Yuejun.Mathematical Model and Method for the Spontaneous Potential Well－Logging［J］.European Journal of Applied Mathematics，1994，5：123－139.

［7］ 李海龙.均匀地层中自然电位测井方程的“精确解”［J］.数学年刊，1996，17A（1）：87－96.

［8］ Zhou Yi，Cai Zhijie.Convergence of a Numerical Method in Mathematical Spontaneous Potential Well－Logging［J］.European Journal of Applied Mathematics，1996，7（1）：31－41.

［9］ 李大潜.有限元素法在电法测井中的应用［M］.北京：石油工业出版社，1980.

［10］Li Tatsien，et al.Boundary Value Probelms with Equivalued Surface and Resistivity Well－Logging，Pitman Research Notes in Mathematics Series 382，Chapman ＆Hall／CRC，1998.

［11］Adams R A.索伯列夫空间［M］.叶其孝，王耀东，应隆安，等译.北京：人民教育出版社，1981.

［12］彭跃军，一类偏微分方程的边值问题适定的充分必要条件［J］.同济大学学报，1988，16（1）：91－100.

［13］Gilbarg D，Trudinger N S.二阶椭圆型偏微分方程［M］.叶其孝，等译.上海：上海科学技术出版社，1981.

［14］陈亚浙，吴兰成.二阶椭圆型方程与椭圆型方程组［M］.北京：科学出版社，1991.

［15］Cai Zhijie.Asymptotic Behavior for a Class of Elliptic Equivalued Surface Boundary Value Problem with Discontinuous Interface Conditions［J］.Applied Mathematics，A Journal of Chinese Universities，Ser.B，1995，10（3）：237－250.

［16］李大潜.有限元素法续讲［M］.北京：科学出版社，1979.

［17］左立华，陈娓.自然电位测井的双层位势法［J］.工程数学学报，2008，25（6）：1013－1022.

［18］陈娓，左立华.自然电位测井数学模型的一类求解方法［J］.应用数学学报，2009，32（4）：732－745.

［19］Kellogg O D.Foundations of Potential Theory［M］.Berlin：Springer－Verlag，1929.

［20］复旦大学数学系.数学物理方程：2版［M］.上海：上海科学技术出版社，1961.

Mathematical Modeling and Numerical Method for the Spontaneous Potential Well－logging

LI Tatsien1，CAI Zhijie1，CHEN Wei2，TAN Yongji1，WANG Wenjuan1，WANG Jingnong3
（1.School of Mathematical Sciences，Fudan University，Shanghai 200433，China；2.School of Mathematics and Information，Shanghai Lixin University of Commerce，Shanghai 201620，China；3.Technical Center，China Petroleum Logging CO.LTD.，Xi’an，Shaanxi 710021，China）

Spontaneous potential well－logging is a useful method for the petroleum exploration and exploitation.Based on a series of previous results published separately in diverse journals and a recent research，the authors provide a complete theoretical and numerical framework of the mathematical modeling and numerical method together with examples and applications for the spontaneous potential well－logging in the axi－symmetric case.The contents consist of mathematical model and its well－posedness，limit behavior of solutions and a reduced mathematical model，efficient numerical methods，examples and applications.

spontaneous potential well－logging，axi－symmetric case，mathematical modeling，numerical method

P631.321；O29

A

2012－04－05 本文编辑 王环）

1004－1338（2012）03－0211－14

1复旦大学数学科学学院，E－mail：dqli＠fudan.edu.cn；2上海立信会计学院数学与信息学院，E－mail：weichen418＠gmail.com；3中国石油集团测井有限公司技术中心，E－mail：wangjingnong123＠163.com