二维复杂泥浆侵入阵列感应测井响应模拟与分析

刘迪仁，谢伟彪，袁继煌，殷秋丽，王洪亮，吴立峰

（1.油气资源与勘探技术教育部重点实验室（长江大学），湖北荆州434023；2.长江大学地球物理与石油资源学院，湖北荆州434023；3.中国石油西部钻探工程公司测井公司，新疆克拉玛依834000）

二维复杂泥浆侵入阵列感应测井响应模拟与分析

刘迪仁1，2，谢伟彪1，2，袁继煌3，殷秋丽1，2，王洪亮3，吴立峰1，2

（1.油气资源与勘探技术教育部重点实验室（长江大学），湖北荆州434023；2.长江大学地球物理与石油资源学院，湖北荆州434023；3.中国石油西部钻探工程公司测井公司，新疆克拉玛依834000）

实际测井环境中泥浆侵入使井眼附近地层电阻率径向变化，因地层非均质性使电阻率在侵入带呈现二维复杂分布。这种复杂泥浆侵入是阵列感应测井响应的主要影响因素之一。基于正演计算，模拟渐变的泥浆侵入前缘和侵入带电阻率二维分布环境下阵列感应测井的响应，研究该复杂泥浆侵入环境下泥浆侵入前缘角度和侵入深度对阵列感应测井响应的影响。可为解释工作中消除复杂泥浆侵入对阵列感应测井响应的影响提供一定的理论参考。

阵列感应测井；泥浆侵入；正演计算；侵入前缘

0 引 言

感应测井是重要的电阻率测量方法［1］。阵列感应测井克服了常规双感应测井纵向分辨率差、探测深度不固定、不能有效划分渗透层和解释复杂侵入剖面等缺点［2］。阵列感应测井数据经过处理后可以得到地层真电阻率、冲洗带电阻率及侵入深度，从而得到直观形象的泥浆侵入剖面［3］。

阵列感应测井仪器由多个不同间距的子阵列组成，测井响应特征受趋肤效应、围岩效应、井眼和侵入影响，并与仪器的线圈间距布置紧密相关。由于测井环境的复杂性，在评价解释工作中必须要消除围岩、泥浆滤液侵入、井眼等地层环境的影响［4］，进而得到精确的地层电阻率。其中泥浆侵入是致使阵列感应测井响应曲线出现异常的主要原因之一，对阵列感应测井响应的影响很大。因为泥浆及其滤液侵入储集层受流体性质、重力等影响，即在侵入带外边界受到相同压力差作用时，在同一地层中不同深度侵入深度不同，通过二维泥浆侵入数值模拟发现把侵人带前缘可以近似看成单一阶梯状突变［5］。本文基于正演计算，模拟了渐变的泥浆侵入前缘和侵入带电阻率二维分布环境下阵列感应测井的响应特性，研究了这种复杂泥浆侵入环境下泥浆侵入前缘角度和侵入深度对阵列感应测井响应的影响，意为测井解释中消除复杂泥浆侵入对阵列感应测井响应的影响提供一定的理论参考。

1 阵列感应测井响应计算

感应测井的发射电流是时间的正弦函数，当源距较大时一般可等效为磁偶极子进行计算。在垂直井中发射线圈为Z方向的磁偶极子（见图1）。Z方向上的单位磁偶极子在均匀介质中产生的Hertz势可表示为［6］

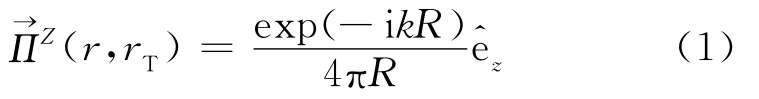
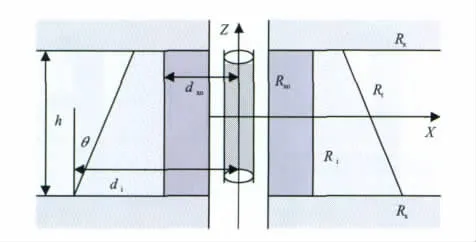
图1 地层模型

Hertz势与电场的关系为

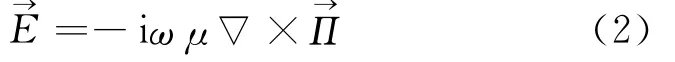
由式（2）可以得出发射线圈在地层各点产生的电场。接收线圈的二次磁场可以表示为背景场和散射场的迭加［7］

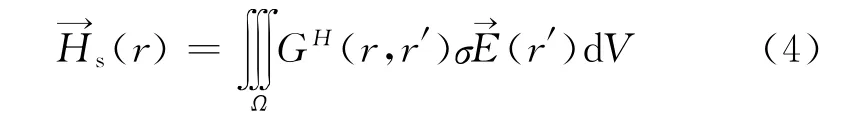
式中，GH为磁型Green函数。式（4）中电场可由式（2）求出。双线圈系视电导率为

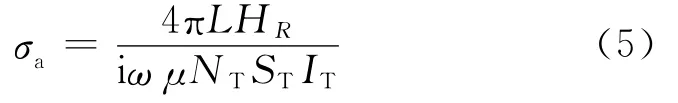
依照上述计算过程进行编程，通过双线圈系和复合线圈系视电导率关系，得出复合线圈系视电导率值，进而得出视电阻率。根据地层模型（见图1）将地层划分为N个小体积元，式（4）的积分可以表示为

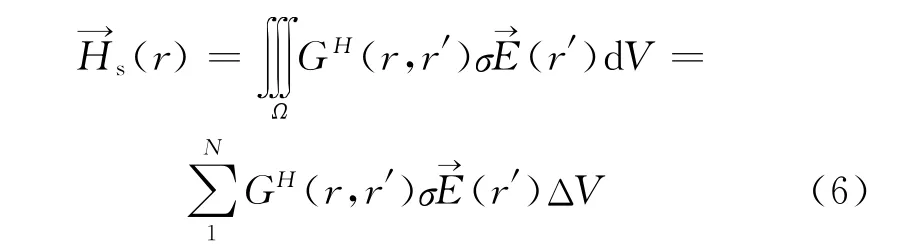
式中，ΔV表示小体积元的体积，由式（1）计算Hertz势，代入式（2）计算出空间各点的电场，进而由式（3）、式（4）、式（6）求出接收线圈处的二次磁场，再根据式（5）得出阵列感应测井视电导率值。

2 地层模型

在垂直井中，由于泥浆侵入，在地层中形成侵入前缘渐变的侵入带。二维泥浆侵入带前缘可以近似看成单一阶梯状突变［5］，复杂侵入地层模型见图1。目的地层层厚为h；冲洗带径向深度为dxo；过渡带径向深度为di；侵入前缘角度为θ；地层电阻率为Rt；围岩电阻率为Rs；冲洗带电阻率为Rxo；过渡带电阻率为Ri；井眼泥浆电阻率为Rm。

在河南乃至全国农资界，不知道范国防这个名字的人不多。前不久，笔者到南宁参加了一次会议，有幸当面聆听了范国防这位绿业元集团公司掌舵人的一次演讲。可以毫不夸张地说，他领导的绿业元公司，这几年创造了农资行业的一个个销售神话：2017年销售额实现10.17亿元；进入2018年，刚刚到6月底，销售就突破了15亿元大关，仅6月份一个月销售额就达到5.23亿元。在谈到自己的销售经验时，范国防提出的“人、品、法”经营法则，让所有参会者为之折服。

在某一深度点，侵入带电导率径向变化通常可以用三参数、四参数（指数侵入模型）和五参数模型表示。在高电阻率泥浆侵入和低电阻率泥浆侵入时，通过泥浆侵入数值模拟发现四参数模型更符合实际泥浆侵入规律。本文用指数侵入模型（四参数模型）描述侵入带电导率［8］，其公式为

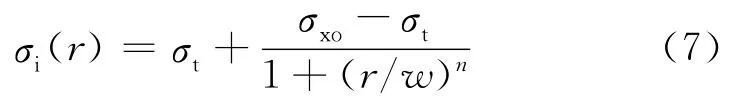
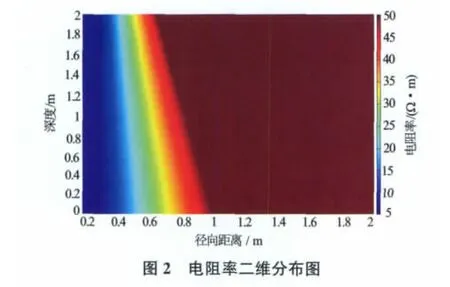
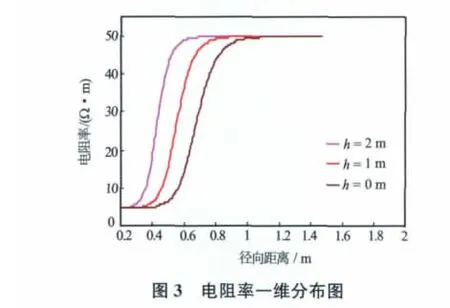
侵入带电阻率Ri（r）＝1／σi（r）；式（7）中σt＝1／Rt；σxo＝1／Rxo；w是电导率为过渡带电导率与地层电导率之和一半（过渡带中心）对应的侵入深度；n是过渡带指数。设n＝10，Rt＝50Ω·m，Rxo＝5Ω·m，θ＝10°，di＝1m，h＝2m时电阻率径向二维分布见图2。图3是图2中纵向深度为0、1、2m位置的电阻率一维分布图。

泥浆侵入在地层中形成渐变的侵入前缘，其前缘倾斜角度可以根据自然电位值、泥浆侵入二维数值模拟和二维时间推移测井等方法得出［5，9］，侵入前缘角度与地层孔隙度、地层水矿化度、沉积过程等地质因素和泥浆矿化度等钻井因素有关。

3 泥浆侵入时阵列感应测井响应分析

以AIT－H阵列感应测井仪器进行研究分析。AIT－H阵列感应测井仪器有8个子阵列，发射线圈到主接收线圈距分别为6、9、12、15、21、27、39、72 in＊＊非法定计量单位，1ft＝12in＝0.304 8m，下同。AIT－H阵列感应测井仪器频率为26.325 kHz，其仪器结构图见图4。

图4 AIT－H仪器线圈分布

3.1 阵列感应测井响应模拟

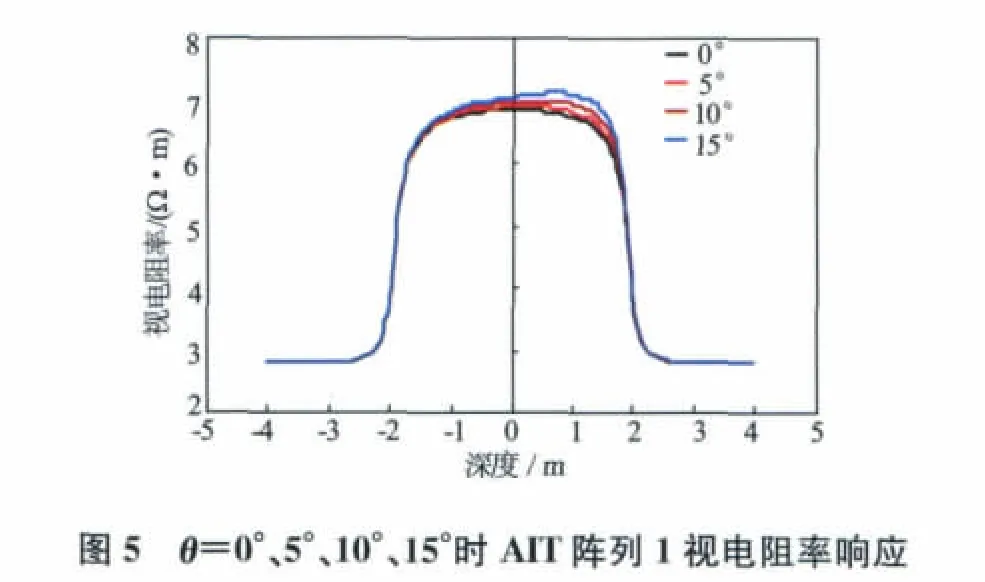
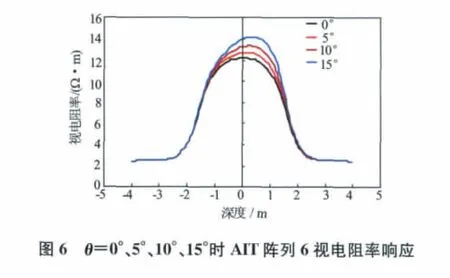
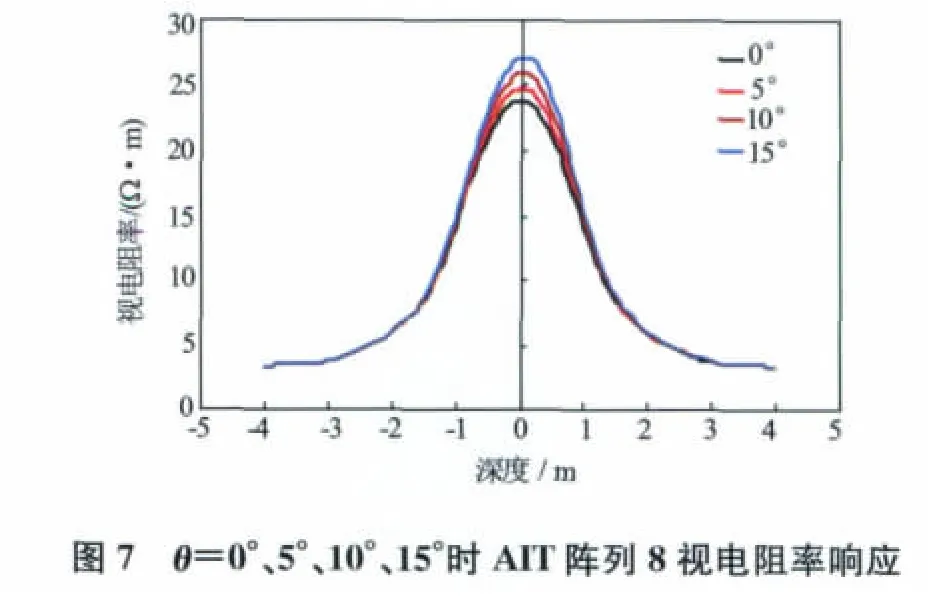
在数值研究分析中，地层电阻率Rt＝50Ω·m，冲洗带电阻率Rxo＝5Ω·m，（井眼电阻率Rm＝Rxo），围岩电阻率Rs＝2Ω·m，侵入带侵入前缘角度θ＝0°、5°、10°、15°，侵入深度di＝1.5m，目的地层层厚h＝4m。

由图5至图7可以得出，渐变侵入前缘对阵列感应测井的曲线形状和视电阻率响应值有很大影响。随着侵入前缘倾斜角度增大，对过渡带比较敏感的子阵列曲线峰值出现偏移，峰值向目的地层上半地层移动，并且侵入前缘角度越大，其峰值偏移也明显。阵列8由于径向探测深度大，其视电阻率曲线峰值基本不随侵入带前缘角度增大而发生偏移。随着侵入前缘倾斜角度增大，子阵列视电阻率响应值接近地层真电阻率。由于侵入前缘倾斜角度的影响，不同探测点的径向侵入深度不一样，对过渡带比较敏感的子阵列在不同探测点受到的不同径向侵入深度的侵入带影响，从而造成峰值向目的地层上半地层偏移的现象。侵入前缘角度增大，侵入带减小，径向探测较深的子阵列受到侵入的影响减小，故而视电阻率接近地层真电阻率。

在阵列感应测井软聚焦处理和利用阵列感应测井反演地层径向电阻率时应该着重考虑侵入前缘倾斜对阵列感应测井响应带来的影响。

3.2 侵入前缘角度影响分析

图8为AIT阵列感应测井各子阵列随侵入前缘倾斜角度变化关系图。由图8可以看出各子阵列视电阻率随着侵入前缘倾斜角度增大而逐渐接近地层电阻率值；各子阵列随着径向探测深度增大，其对侵入带的敏感度不同，在侵入前缘倾斜角度增大时对侵入带敏感的子阵列视电阻率变化也越明显。侵入前缘倾斜角度增大，侵入带区域减小，各子阵列受到泥浆侵入的影响也减小，故而视电阻率接近地层真电阻率。

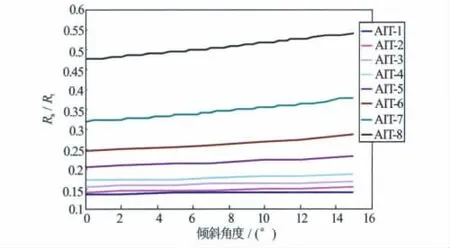
图8 AIT阵列感应随角度变化

为了研究各子阵列随角度变化关系，图9是各子阵列在侵入前缘倾斜时视电阻率与各子阵列在侵入前缘非倾斜（θ＝0°）时视电阻率的比值随倾斜角度的变化关系。

图9反映了随着侵入前缘倾斜角度变化，各子阵列视电阻率值相对侵入前缘非倾斜（θ＝0°）时的视电阻率增量。图9中X轴是侵入前缘倾斜角度，Y轴是侵入前缘倾斜角度变化时各子阵列视电阻率值与侵入前缘非倾斜（θ＝0°）时的视电阻率的比值，Ra，0是侵入前缘非倾斜（θ＝0°）时的视电阻率值。由图9可以看出，在Rt＞Ri＞Rxo情况下，随着侵入前缘倾斜角度增大，各子阵列视电阻率值增大，并且侵入前缘倾斜时视电阻率与侵入前缘非倾斜（θ＝0°）时视电阻率的比值与侵入前缘倾斜角度的关系近似为斜率一定的直线关系，其斜率大小与各子阵列径向探测深度相关。阵列感应测井各子阵列对侵入带越敏感，其对应的斜率也越大，各子阵列对应的斜率值关系为k1＜k2＜k3＜k4＜k5＜k6＜k7且k7＞k8，k8是阵列8对应的斜率，由于阵列8径向探测深度大，其视电阻率受侵入带前缘角度影响小，从而k8＜k7。由此，可得阵列感应测井各子阵列对应的斜率与各子阵列径向探测深度和侵入深度是相关的。

图9 视电阻率比值随倾斜角度变化

3.3 侵入深度影响分析

侵入深度对阵列感应测井的影响研究在文献［11］中已经有详细报道，这里不再分析，可以看出上述k值能简化侵入前缘渐变的侵入环境校正。

在地层模型其他条件不改变，不同侵入深度下，子阵列AIT－1、AIT－6、AIT－8在侵入前缘倾斜时视电阻率与各子阵列在侵入前缘非倾斜（θ＝0°）时视电阻率的比值随倾斜角度的变化关系见图10。

由图10得出，在不同侵入深度下子阵列在侵入前缘倾斜时视电阻率与各子阵列在侵入前缘非倾斜（θ＝0°）时视电阻率的比值随倾斜角度的变化关系近似为斜率一定的直线关系（即k值一定的直线），并且其直线斜率随着侵入深度增大而减小（k值减小）；侵入深度对子阵列4、5、6、7的k值影响较大，对阵列8的k值影响较小。子阵列4、5、6、7径向探测范围对泥浆侵入敏感，从而侵入深度对子阵列4、5、6、7的k值影响较大；阵列8径向探测深度大，侵入带对其视电阻率影响较小，从而侵入深度对子阵列8的k值影响小。

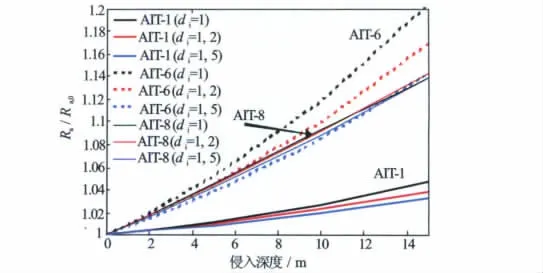
图10 不同侵入深度下视电阻率比值随倾斜角度变化

在对侵入前缘倾斜的复杂侵入带进行校正时，可以考虑按上述情况先根据侵入前缘倾斜角度将视电阻率校正到侵入前缘非倾斜的侵入带环境下的视电阻率，然后再进行侵入校正，将视电阻率校正为地层真电阻率，其前缘倾斜角度可以根据自然电位值、泥浆侵入二维数值模拟和二维时间推移测井等方法得出。

4 结 论

（1）基于正演计算，模拟了渐变的泥浆侵入前缘和侵入带电阻率二维分布环境下阵列感应测井的响应特性；研究了该复杂泥浆侵入环境下泥浆侵入前缘角度和侵入深度对阵列感应测井响应的影响。

（2）渐变侵入前缘对阵列感应测井的曲线形状和视电阻率响应值有很大影响。随着侵入前缘倾斜角度增大，对过渡带比较敏感的子阵列曲线峰值出现偏移，峰值向目的地层上半地层移动，并且侵入前缘角度越大，其峰值偏移也越明显。

（3）随着侵入前缘倾斜角度增大，阵列感应测井各子阵列视电阻率响应值接近地层真电阻率，并且侵入前缘倾斜时视电阻率与侵入前缘非倾斜（θ＝0°）时视电阻率的比值与侵入前缘倾斜角度的关系近似为斜率一定的直线关系，其斜率大小与各子阵列径向探测深度和侵入深度相关。

（4）在不同侵入深度下子阵列在侵入前缘倾斜时视电阻率与各子阵列在侵入前缘非倾斜（θ＝0°）时视电阻率的比值随倾斜角度的变化关系近似为斜率一定的直线关系，并且其直线斜率随着侵入深度增大而减小。

（5）在对侵入前缘倾斜的复杂侵入带进行校正时，可以考虑按上述情况先将视电阻率校正到侵入前缘非倾斜的侵入带环境下的视电阻率，然后再进行侵入校正。

［1］ 汪功礼，张庚骥，崔锋修，等.三维感应测井响应计算的交错网格有限差分法［J］.地球物理学报，2003，46（4）：561－567.

［2］ Randy Beste，Hagiwara T，George King，et al.A New High Resolution Array Induction Tool［C］∥SPWLA 41st Annual Logging Symposium，June 4－7，2000.

［3］ 丁娱娇，邵维志，李庆合，等.一种利用阵列感应测井技术识别储层流体性质的方法［J］.测井技术，2009，33（3）：238－242.

［4］ Tom Barber，Tracy Broussard，Barbara Anderson，et al.3DInduction Log Modeling as a Practical Aid to High－angle and Horizontal Well Interpretation［C］∥SPWLA 41st Annual Logging Symposium，June 4－7，2000.

［5］ 常文会，潘和平，周峰.泥浆侵入二维数值模拟［J］.中国地质大学学报：地球科学版，2010，35（4）：674－680.

［6］ 魏宝君，王甜甜，王颖.用磁流源并矢Green函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应［J］.地球物理学报，2009，52（11）：2920－2928.

［7］ 陈桂波，汪宏年，姚敬金，等.用积分方程法模拟各向异性地层中三维电性异常体的电磁响应［J］.地球物理学报，2009，52（8）：2174－2181.

［8］ 国庆忠.利用阵列感应测井资料反演地层径向电导率［J］.测井技术，2003，27（3）：207－211.

［9］ 王斌，范晓敏，陈启艳，等.用有限差分法模拟自然电位测井的侵入带影响［J］.测井技术，2008，32（2）：164－168.

［10］仵杰，冯娟，解茜草，等.泥浆侵入地层中高分辨率感应测井响应特征的正演分析［J］.测井技术，2009，33（3）：212－217.

Simulation and Analysis of Array Induction Log Response for Complicated Two－dimensional Mud Invasion

LIU Diren1，2，XIE Weibiao1，2，YUAN Jihuang3，YIN Qiuli1，2，WANG Hongliang3，WU Lifeng1，2
（1.Key Laboratory of Exploration Technologies for Oil and Gas Resources（Yangtze University），Jingzhou，Hubei 434023，China；2.Geophysics and Oil Resource Institute of Yangtze University，Jingzhou，Hubei 434023，China；3.Wireline Logging company，Xibu Drilling Engineering CO.LTD.，CNPC，Karamay，Xinjiang 834000，China）

In actual logging environment，the invaded area’s resistivity complexity not only involves various radial resistivity profiles，but also two－dimensional distribution nearby wellbore due to the heterogeneous anisotropic formation.The complex mud invasion is one of the important factors affecting the array induction log responses.Based on forward modeling，we simulate the array induction log response in the environment with gradually changing invading front and two－dimensional resistivity distribution，and analyze the effects on the log responses with different invading front angles and invading depths.The conclusion can afford a theoretical reference to correct the effect of complex mud invasion in interpretation work.

array induction logging，mud invasion，forward modeling，invading front

P631.84

A

2011－12－02 本文编辑 李总南）

1004－1338（2012）03－0234－05

国家自然科学基金项目“伪随机扩频脉冲在地球介质中的传播特性研究”资助（No.40774073）

刘迪仁，男，1965年生，副教授，博士，从事电法测井正反演、复杂储层测井评价及光纤传感技术等方面的理论和应用研究。