基于覆盖性能的W alker-δ星座构型保持

杨晓龙，刘忠汉

（北京控制工程研究所，北京 100190）

基于覆盖性能的W alker-δ星座构型保持

杨晓龙，刘忠汉

（北京控制工程研究所，北京 100190）

考虑到Walker-δ星座中各星相互协作关系，提出一种基于覆盖性能的星座构型保持策略.作为策略判别指标的覆盖性能由一种改进的网格点仿真法获取.这种改进方法依照卫星星下点与网格点的几何关系，可以快速判断处于覆盖区的网格点，然后统计出星座的全球覆盖信息.卫星的标称位置是考虑J2项摄动长期影响得到的动态位置.星座运行过程中，一旦发现不满足覆盖要求的点，结合各卫星的标称位置，可以找出影响覆盖性能的卫星.最后将该卫星调整到标称位置即可完成构型保持.最后给出构型保持策略的仿真算例，仿真结果表明了策略的有效性.

Walker-δ星座；构型保持；覆盖性能；网格点仿真

20世纪70年代 Walker星座概念被提出了［1］，随后吸引了众多学者对其进行研究.虽然后来也陆续出现其他构型的星座，但Walker星座仍然因其优秀的全球、纬度带覆盖性能被许多大型星座系统所采用，例如美国的 GPS全球导航定位系统、俄罗斯的Glonass导航系统、欧盟部署的Galileo卫星导航系统、Iridium系统和“Globalstar”语言移动通讯系统，此外还有一些采用复合构型的星座也包含Walker星座.因此研究Walker星座的构型保持具有典型意义.

1 W alker-δ星座构型

Walker星座包含星形星座、δ星座、σ星座、ω星座和玫瑰星座，其中δ星座应用得比较广泛，因此本文选其作为研究对象，称之为Walker-δ星座.

Walker-δ星座的各条轨道高度相同，对于参考平面有相同的倾角，每个轨道面内有相同数目的卫星，其相位均匀分布，各个轨道与参考平面的交点均匀分布，且相邻轨道面的相同编号卫星之间相位差固定.Walker-δ星座构型的可以描述为［2］：

其中N代表星座的卫星总数，P代表轨道面数，i表示轨道倾角，h代表轨道高度，F是表征不同轨道面间卫星相对位置的量，称为相位因子，取值为0到P -1，相邻轨道面的对应编号的卫星之间的相位差即为：

在星座长期运行过程中，入轨偏差、各种摄动力以及每次机动后带来的控制残差都会使卫星逐渐偏离原先设计的标称轨道，逐渐破坏星座构型，引起星座性能的下降.

摄动包括地球非球形摄动、日月三体引力摄动、太阳光压摄动、大气阻力摄动和后牛顿效应摄动，其中地球非球形摄动的 J2项影响比较显著，在 J2项摄动影响下，卫星平均轨道根数的摄动方程为：［3］

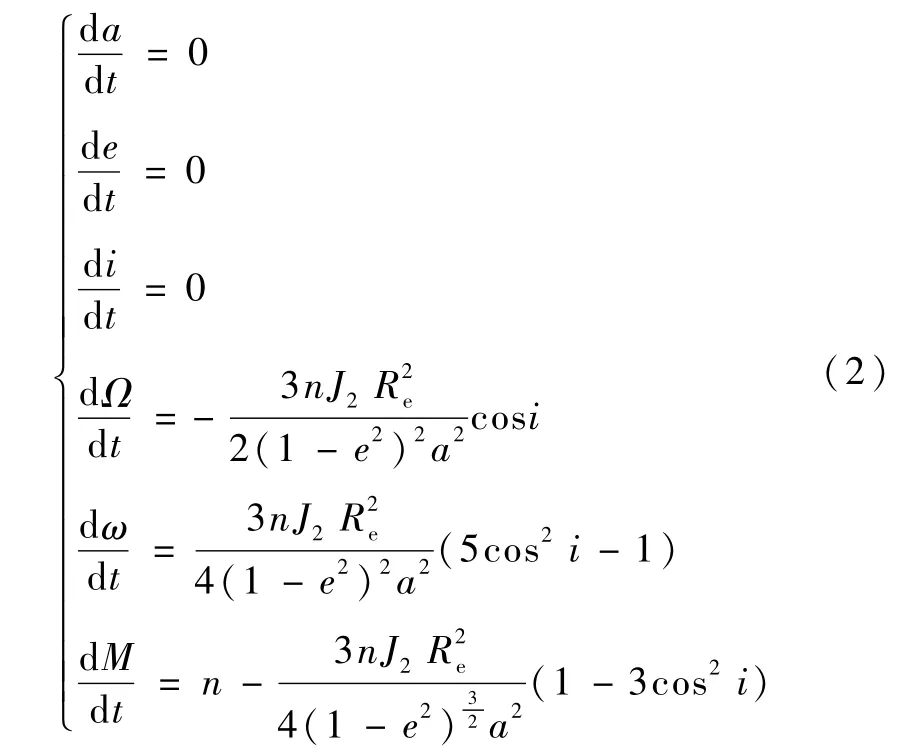
由上式可以看出J2项摄动对半长轴、偏心率和倾角没有长期影响，而会影响升交点赤经、近地点幅角和平近点角.升交点赤经、近地点幅角和平近点角的变化率取决于轨道的半长轴、偏心率和倾角，因此对于同一轨道面的（a，i，e）相同的若干颗卫星变化趋势相同.对于Walker-δ星座来说，每个轨道面的进动速度一样，每个轨道面里的卫星漂移情况相同，所以J2项并不改变星座卫星的相对位置关系.这个特点可以被标称位置选取时利用.

假设卫星的初始偏差为（Δa Δe Δi ΔΩ Δω ΔM）.对于Walker-δ星座来说，其轨道是圆轨道，不存在近地点幅角和平近点角，定义卫星的沿迹角为［4］

则升交点赤经、沿迹角受轨道初始位置偏差的长期摄动变化

2 构型保持策略

国内外学者对于星座构型保持提出了很多策略方案：文献［5］和［6］提出了选取卫星相对标称相位为状态变量的圆轨道星座维持方法，研究中将状态变量取为每颗卫星相对于“平均星座”的相位.文献［7］提出了星座位置保持的时间-目标方法（timedestination approach）.文献［8］利用线性二次控制器来实现星座的位置保持.文献［9］对利用线性规划法实现卫星星座位置保持进行了研究.文献［10］提出了一种直接控制卫星间的间距的分布式控制方案.文献［11］研究了在考虑最少燃料消耗和时间限制等多目标情况下的卫星星座轨道位置保持的最优机动问题，等等.然而这些策略大多数尚处于仿真理论阶段，在实际星座运行管理阶段进行应用并得到验证的是一种名叫“控制盒子”的方法.

“控制盒子”法是对于星座中每颗卫星选取一个控制基准，然后根据任务性能指标和星座构型参数设定一个最大容许偏差，可以表达为卫星轨道要素的最大容许偏差.最大容许偏差与控制基准一起确定了卫星保持的一个三维控制盒子（3D control box）.构型保持的目标就是使所有卫星始终处于其盒子里，一旦卫星漂移出盒子边缘便对其进行机动.文献［4］、［12］给出了最大容许偏差不同的计算方法.文献［13］讨论了卫星位置控制三维盒子对覆盖的影响、三维盒子与轨道根数的关系，还对星座相位保持中的超调控制、控制盒子以及轨道根数漂移范围的确定方法等进行了研究.

“控制盒子”法通过设定控制基准和最大容许偏差将整个星座的构型保持分解为每颗星的独立控制，虽然可以使构型保持任务简单化并提高系统的可靠性，但在任务指标与控制基准和最大容许偏差转化时并不完全等价.比如利用星座的覆盖要求求出的卫星最大容许偏差，这个值不应该是个特定的值.因为星座要对某个地点实现N重覆盖时总是需要至少N颗星协作，对于其中一颗星而言，其他相邻卫星的位置也会影响它的容许偏差.这样在实际构型保持中若按照某一固定容许误差作为判别依据，要么偏于保守，浪费燃料，要么构型已经破坏，却没做出相应的调整.

制定构型保持策略时要将星座作为一个系统来考虑，要考虑所有卫星的状态.构型保持策略的控制判别条件也不能仅仅依照单星的偏移量，而是要考虑卫星状态量对整体性能的影响效果.对于很多星座任务，比如导航、通信、侦察，良好的对地覆盖都是其最基本的、重要的性能要求.与其他构型的星座相比，全球的覆盖性能也是Walker-δ星座的优点.由于星座的覆盖性能是由所有卫星协作实现的，因此它能在一定程度上反映星座的整体状态.本文就基于覆盖性能设计一个Walker-δ星座的构型保持策略.它不再试图寻找最大容许偏差的计算方法，而是回归到星座最初的性能要求，利用采样点统计出星座实时的覆盖性能，进而判断是否需要保持操作.这样可避免前面所述“控制盒子”法的缺点，更加契合星座中各星协作运行的特点.

这个构型保持策略包含构型保持判别指标、调整对象的确定、调整对象标称位置的确定.在星座运行期间，一旦发现判别条件满足，就可按照设计算法找到需要调整的目标星，算出其标称位置.而后依靠底层的轨道机动将目标星送到标称位置，就可进入下一个保持周期.下面就详细介绍设计的保持策略：

2.1 判别指标

构型保持策略中采用一种改进的网格点仿真法来获取Walker-δ星座全球覆盖性能，作为保持判别的指标.这里选取覆盖重数作为覆盖性能来说明.

传统的网格点仿真法就是在地球球面上选取很多点，这些点一般沿纬度线均匀选取，然后就利用视函数法或者地心角法来计算星座运行期间这些点与每颗卫星的相对关系，最后再进行统计分析，获取相关覆盖性能指标.其中地心角法如下：

设卫星轨道高度为H，地球半径为R，地面点P的最小仰角为ε，则卫星覆盖区域最大地心角为

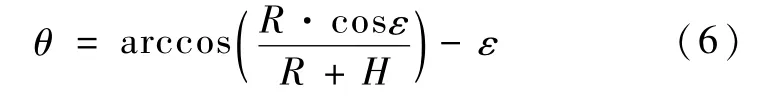
假设网格点总数是 N1，对于一颗卫星来讲，要依次计算与这 N1个点的地心角，若小于等于最大地心角θ，则说明该点在该卫星的覆盖区域.这样在每一个采样周期里要计算（N·N1）次地心角.但对于一颗星来说，其覆盖区域不会超过球面的1/2，所以每次计算至少一半的点不在其覆盖区内，为减少这种计算量，这里给出一种结合解析式的改进方法.

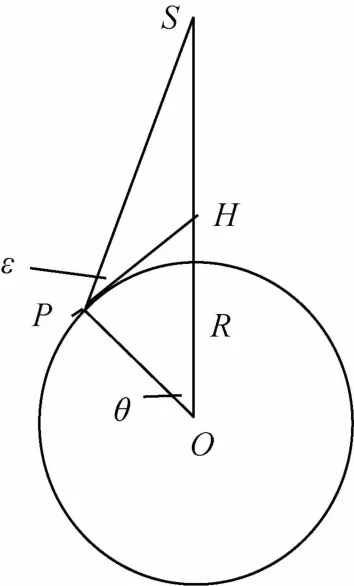
图1 卫星对地覆盖图Fig.1 Satellite coverage geometry

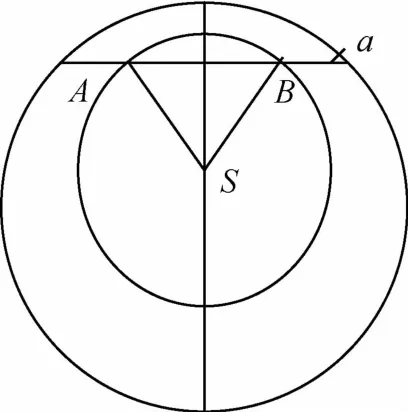
图2 覆盖区内纬度线区段示意图Fig.2 Latitude in the coverage region

图1 ～2中 S为星下点，其赤经、赤纬为（λ，φ），横线为a度的纬度线.小圆是卫星覆盖区域，A，B是区域与a度纬度线的交点，则a度纬度线在覆盖区的范围为（λA，λB）.下面来计算：

对于A点有

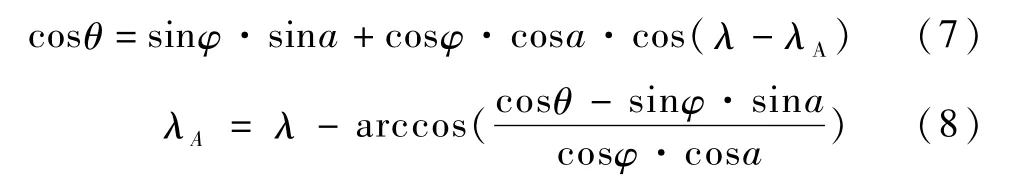
类似的，对于B点有：

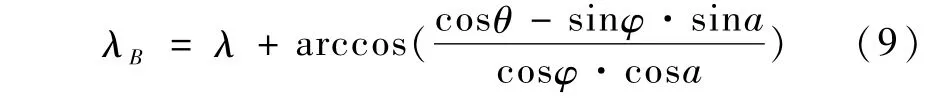
再据此判断位于该区段的网格点.

若覆盖区域最北端越过北极点和覆盖区域最南端越过南极点，做如下处理：

1）当覆盖区域最北端越过北极点，即（φ+θ）≥90°，则处于［180。-（φ+θ），90。］区间的纬度线所

因此a度纬度线上的被覆盖区段为：有的网格点均被覆盖；

2）当覆盖区域最南端越过南极点，即（φ-θ）≤-90°，则处于［-90。，-180。-（φ-θ）］区间的纬度线所有的网点均被覆盖.

其他的纬度线仍依据前面的方法计算.

这样在一个保持周期里，只需对每颗卫星进行上述计算、判断，就可以统计出全球的各网格点的覆盖重数.在同样条件下，耗费时间比传统的网格点法的少，其比值大致相当于单星对地覆盖面积与全球面积的比值.

若任务要求星座实现N重覆盖，由上述方法得到覆盖重数一旦有低于N的话，就开始进行保持操作.

这种网格点法由于采用了离散采样的方法，对任务覆盖要求有极强的适应性.不管是全球一致覆盖要求，还是纬度带覆盖要求，甚至是不规则区域的特殊覆盖要求都可以通过修改相应采样点的期望覆盖值来表现.

2.2 目标星和标称位置的确定

由式（2）已知，在J2项摄动的影响下，各个轨道面的Ω漂移，且变化率一致，表现为整个星座是在惯性空间里缓慢转动.λ的漂移也是相同的，这样平面内卫星间相位间距不变.星座全球覆盖性能也不会下降.为减少机动的燃料消耗，选取标称位置如下：

其中n为轨道平均角速度.a，i，e认为不变.

考虑到轨道面的调整需要耗费的燃料很多，而轨道面内的轨道机动比较容易，因此只调整目标星的沿迹角到标称位置.

在得到各网格点的覆盖重数后，若发现重数低于N的网格点，则用地心角法计算当前覆盖它的所有的卫星的编号，记为数组A1.然后依照式（10）、式（11）计算该时刻的所有卫星的标称轨道根数，再跟覆盖重数低于N的网格点进行计算，获取能够覆盖它的所有卫星编号，记为数组A2.比较A1和A2，就可知道哪几颗卫星因为偏离影响了覆盖性能.若该点覆盖重数为（N-1）重，为节省燃料只须调整一颗沿迹角偏差最大的满足覆盖要求即可.

2.3 构型保持策略流程

依据前面所述，整个构型保持策略流程如下：

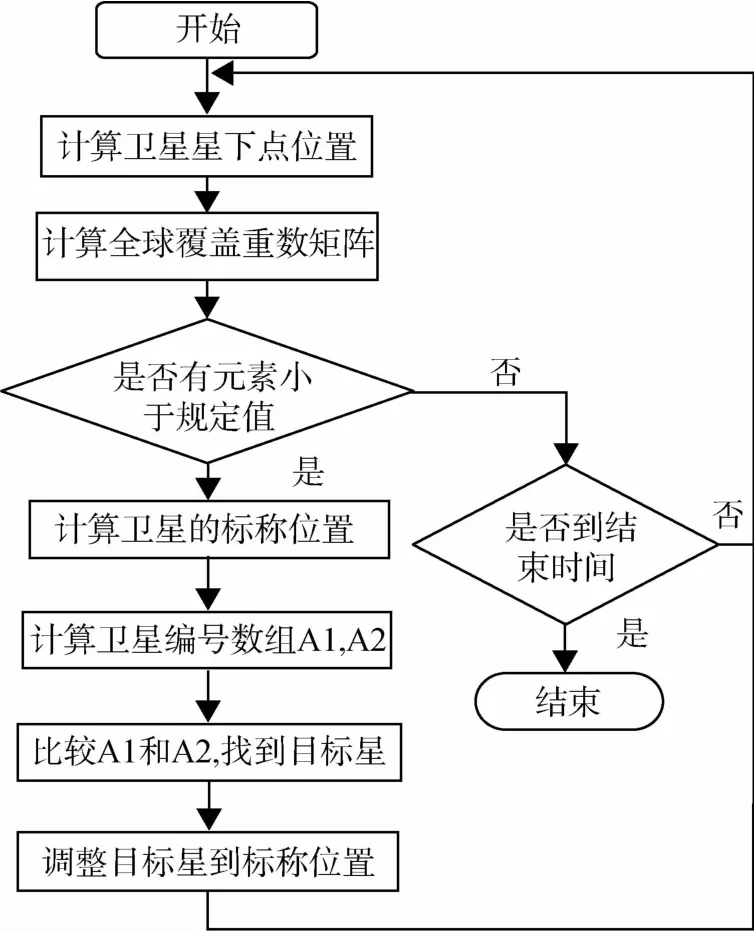
图3 构型保持策略流程图Fig.3 Flow chart of configuration maintenance strategy

3 仿真算例

仿真对象Walker-δ星座为24/3/1，倾角55。，高度21500km.该星座满足至少6重全球覆盖.设定轨道根数（a，i，e，Ω，λ）存在初始偏差.在仿真星座运行过程中，假定a，i，e不变，摄动模型只考虑了J2项，但这并不影响验证控制策略的有效性.卫星最小仰角5。.网格点沿纬度线选取，间隔为6。，赤道上选取60个点，为保证取点的均匀性，其他纬度上的点数与其纬度的余弦值成正比.南、北极点各取一个点.样点总数为1148.采样时间T=60s，仿真时间为365天.卫星编号第一个数字代表轨道面编号，第二个数字代表轨道面里卫星编号.仿真获得的数据如表1所示.

表1 仿真的数据Tab.1 Simulation results

由仿真结果可以看出，在每次星座构型被破坏时，其目标星的相位偏差都不同，这也验证了第2节所说的容许偏差不是固定的值，与相邻卫星的位置也有关系.

4 结 论

本文针对Walker-δ星座的整体性，设计了一种基于覆盖性能的构型保持策略.该策略利用网格点仿真法获取全球覆盖性能.为减少仿真计算开支，本文结合星下点与网格点的相对几何关系对传统网格点法进行了改进.标称位置的选取考虑了J2项摄动的长期影响，给出了动态的升交点赤经和沿迹角标称量.当出现不满足覆盖要求的网格点时，结合卫星的标称位置，可以找出影响覆盖性能的卫星.最后依靠轨道机动将目标星调整到标称位置即可.

虽然仿真算例验证了该策略的有效性，但在实际的构型保持过程中还要考虑很多方面，如燃料消耗均匀性、机动频次限制以及星座其他性能方面的约束.因此，未来的研究是要在更多约束条件、更高的精度模型下对该构型保持策略进行验证、改进.

［1］ Walker JG.Some circular orbit patterns providing continuous whole Earth coverage［J］.Journal of the British Interplanetary Society，1971，24（1）：369-384

［2］ 张育林.卫星星座理论与设计［M］.北京：科学出版社，2008 Zhang Y L.Theory and design of satellite constellations［M］.Beijing：Science Press，2008

［3］ 刘林.航天器轨道理论［M］.北京：国防工业出版社，2000 Liu L.Orbit theory of spacecraft［M］.Beijing：National Defense Industry Press，2000

［4］ 项军华.卫星星座构型控制与设计研究［D］.长沙：国防科技大学，2007 Xiang JH.Study on control and design of configuration for satellite constellation［D］.Changsha：National University of Defense Technology，2007

［5］ Lamy A，Pascal S.Station keeping strategies for constellations of satellites［J］.Spaceflight Dynamics，1993，84：819-833

［6］ Brodsky P，Chen SM S.Automatic maneuver planning for maintenance of satellite constellation geometry［C］. Flight Mechanics Symposium Greenbelt，MD，May 19-21，1997

［7］ Glickman R E.TIDE：The timed-destination approach to constellation formation-keeping［C］.The 4thAAS/ AIAA Spaceflight Mechanics Meeting，Cocoa Beach，FL，Feb.14-16，1994

［8］ Ulybyshev U.Long-term formation keeping of satellite constellation using linear-quadratic controller［J］.Journal of Guidance，Control，and Dynamics，1998，21（1）：109-115

［9］ Lasserre E，Dufour F，Bernussou，et al.A linear programming solution to the homogeneous satellite constellation stationkeeping［C］.The 48thInternational Astronautical Congress，Turin，Italy，Oct.6-10，1997

［10］ McInnes C R.Autonomous ring formation for a p lanar constellation of satellites［J］.Journal of Guidance，Control and Dynamics，1995，18（5）：1215-1217

［11］ Marcelo E M R，de Oliverira L S，de Almeida P.Multiobjective optimization approach applied to station keeping of satellite constellations［C］.AAS/AIAA Astrodynamics Conference.Quebec City，Quebec，Canada，Jul.30-Aug.2，2001

［12］ 向开恒，王瑞.卫星星座的动力学与站位保持［A］.现代小卫星技术（五）现代小卫星星座技术与应用论文集，2001 Xiang K H，Wang R.Dynamics and station keeping of satellite constellation［A］.Modern small satellite technology（5），Thesis of technology and application of modern small satellite and constellation，2001

［13］ 白鹤峰.卫星星座的分析设计与控制方法研究［D］.长沙：国防科技大学，1999 Bai H F.Study on analysis design and control of satellite constellation［D］.Changsha：National University of Defense Technology，1999

W alker-δConstellation Con figuration M aintenance Based on Coverage Per form ance

YANG Xiaolong，LIU Zhonghan
（Beijing Institute of Control Engineering，Beijing 100190，China）

Considering the coordinate relationship among satellites of Walker-δconstellation，a configuration maintenance strategy based on coverage performance is proposed in this paper.Coverage performance as a discriminant of strategy is obtained by an improved grid simulation method.According to the geometry relation between grid point sub-satellite point，this improved method can be used to find those grids within coverage zone and obtain global coverage information.Considering J2perturbation the nominal position of satellite is dynam ic.In operation of constellation，when dissatisfied grids are found，the satellite with reduced coverage performance can be found according to its nominal positiion.The configuration maintenance will be accomp lished after the target satellite is ad justed to its nom inal position.A numeric simulation is given.The result demonstrates the effectiveness of the proposed strategy.

Walker-δconstellation；configuration maintenance；coverage performance；grid simulation

V4

A

1674-1579（2012）02-0053-05

杨晓龙（1987—），男，硕士研究生，研究方向为控制理论与控制工程；刘忠汉（1973—），男，研究员，研究方向为控制理论与控制工程.

2011-11-14

DO I：10.3969/j.issn.1674-1579.2012.02.011