时变参数辨识梯度算法稳定性分析*
2012-09-05王丽娇
熊 凯,孟 斌,王丽娇
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
时变参数辨识梯度算法稳定性分析*
熊 凯1,2,孟 斌1,2,王丽娇1,2
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
研究用于时变参数辨识的梯度算法稳定性问题.基于随机过程有界性判据对时变参数辨识梯度算法进行了稳定性分析,给出了梯度算法稳定的充分条件.指出在待辨识参数变化率有界,观测噪声是零均值白噪声,且系统满足持续激励条件的情况下,梯度算法参数选择满足一定条件时,能够确保参数辨识误差的有界性.上述研究与以往工作的不同之处在于稳定性证明过程中仅要求待辨识参数的变化率是有界的,而不要求参数变化率是零均值白噪声.
参数辨识;梯度算法;随机过程;稳定性
参数辨识作为一种数学建模工具,已在工程上获得日益广泛的应用,其重要应用背景是工业过程自动控制.通过参数辨识,可以在不掌握复杂工业过程内部机理的条件下,利用过程的输入输出信息来建立过程的数学模型.常用的系统参数辨识方法包括最小二乘(LS)算法、卡尔曼滤波(KF)算法和梯度算法等[1-2],其中,梯度算法具有应用简便、计算量小等优点,基于特征建模的自适应控制即采用梯度算法进行模型参数辨识[3].应当指出,对于参数变化规律未知的时变系统,参数辨识算法给出的参数估计值不可能收敛于参数真值,也就是说,时变参数估计不存在一致收敛性.在这种情况下,为了考察辨识算法跟踪时变参数的能力,评价时变参数辨识算法的性能,通常不分析辨识算法的收敛性,而是对辨识算法的稳定性进行研究,即分析参数估计误差的有界性.随机过程有界性判据是对时变参数辨识算法稳定性进行研究的重要理论工具,该判据曾用于扩展卡尔曼滤波(EKF)算法及其他非线性滤波算法的稳定性分析[4-6].
具有稳定性是一个参数辨识算法正常工作的基本要求.在工程实践中,常常得不到未知参数准确的先验信息,如果待辨识参数的初始值选的不准,对其估计值会产生什么影响,这是参数辨识算法稳定性研究需要解决的问题.一般认为,如果随着估计时间的增长,参数估计误差有界,并且估计误差逐渐不受初始误差的影响,则该估计算法是稳定的.影响参数辨识算法稳定性的因素很多,参数变化率和测量噪声特性的变化,或参数辨识算法中的参数调整都可能导致估计误差的动态特性发生显著变化,甚至改变参数辨识算法的稳定性[2].如果能够给出参数辨识算法稳定的充分条件,将有助于找出影响算法稳定性的因素,并为算法中的参数调整提供可靠的依据.
在以往的时变参数辨识算法稳定性分析研究中,往往假定待辨识参数的变化率是零均值白噪声[7].但是,对于一些特定的问题,如特征模型参数辨识问题而言,待辨识参数变化率不一定为0,上述假设不符合实际情况.针对这一问题,本文在对参数辨识梯度算法进行稳定性分析的过程中,仅要求待辨识参数的变化率是有界的,而不要求参数变化率是零均值白噪声.考虑到对于通常的工业过程,待辨识参数总是在一定范围内变化的,参数变化率有界的假设条件在实际系统中更易于得到满足.
1 问题描述
本节给出时变参数辨识梯度算法的形式.所研究的系统模型如下所示:
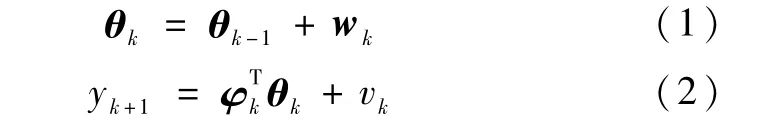
其中,θk∈Rl为待辨识时变参数向量,k表示离散的时间,yk∈R为系统测量输出,φk∈Rl是已知信息向量,测量噪声vk∈ R是零均值白噪声,其统计特性为
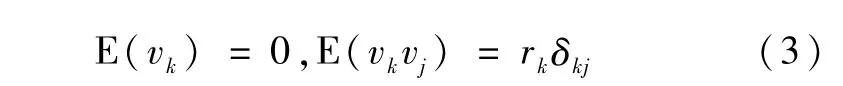
wk是未知参数变化率.本文假设wk是有界的,即

参数辨识梯度算法的目的是确定未知参数 θk的估计值,使得由确定的观测量的预测值接近于实际观测量yk+1.该算法是一种递推算法,即需要给定初始值,第k步的估计值在第k -1步估计值的基础上,根据观测量yk进行修正获得.针对如式(1)和式(2)所示的系统模型,时变参数辨识梯度算法的计算公式可写为如下形式:
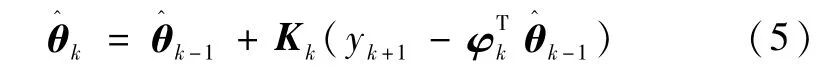
其增益阵为
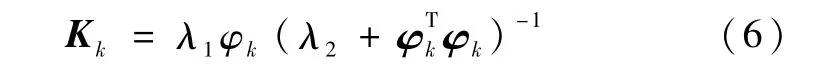
其中,λ1和λ2为梯度算法的设计参数.减小梯度算法中的参数 λ1将增大估计值和的接近程度,从而改善参数估计结果的平稳性,但同时会减弱观测量对参数估计值的修正作用;减小梯度算法中的参数λ2可以增强观测量对参数估计值的修正作用,增强算法对时变参数的跟踪能力,但同时会增大测量噪声vk对参数估计的干扰.参数λ1和λ2的选取可看作对参数辨识平稳性和跟踪能力的折衷.
为了便于后面的稳定性分析,定义辨识算法的参数估计误差为
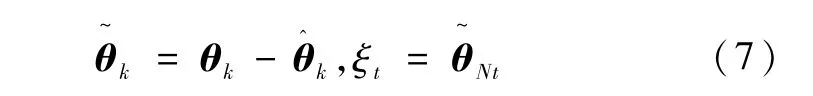
2 随机过程有界性判据
随机过程有界性判据是本文进行时变参数辨识梯度算法稳定性分析的理论基础,该判据可归纳为如下所示的引理形式[4].文中带有随机变量的不等式表示依概率1成立,表示欧氏范数.
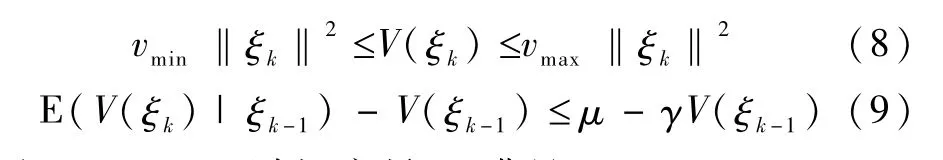
那么∀k∈N,随机变量ξk满足
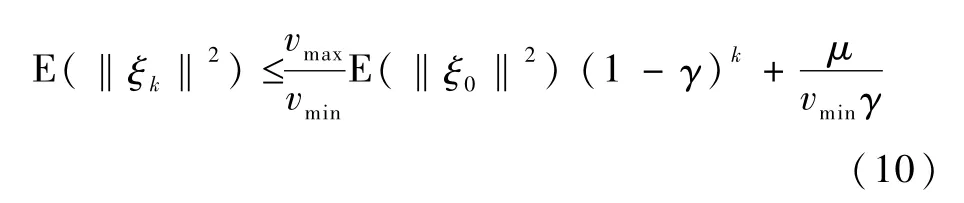
该判据通过比较V(ξk)和V(ξk-1)二者的均值(V(ξk-1)=E(V(ξk-1)|ξk-1))来判断E(‖ξk‖2)是否有界.V(ξk)可视为能量函数.显然,如果直观上可以理解为系统的能量是不断下降的.引理1可视为李雅普诺夫定理的改进形式,只要证明V(ξk-1)小于一个正数 μ减去与一个与 V(ξk-1)成比例的项所得的差.引理1表明,如果不等式(8)和(9)成立,那么由式(10),随着时间 k的增长,随机变量ξk将逐渐不受其初始值ξ0的影响.这一结论与参数辨识算法稳定对估计误差的要求是一致的,因此,引理1比较适合用于分析参数辨识算法的稳定性.
3 引理证明
本节给出时变参数辨识梯度算法稳定性分析过程中需要用到的一个重要引理,并给出相应证明.
引理2.定义转移矩阵
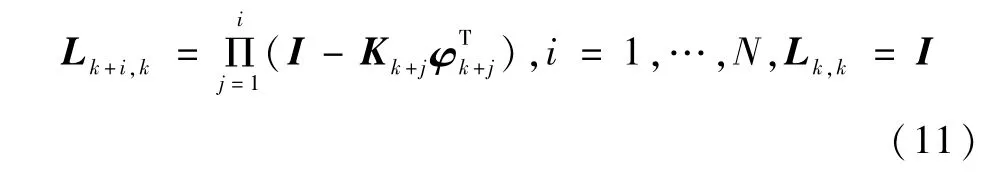
其中,φk∈Rl,N为正整数,
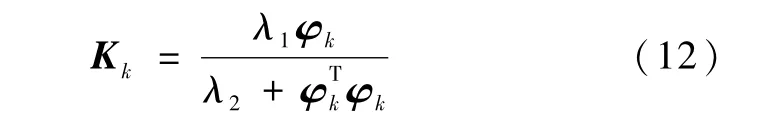
如果φk满足条件
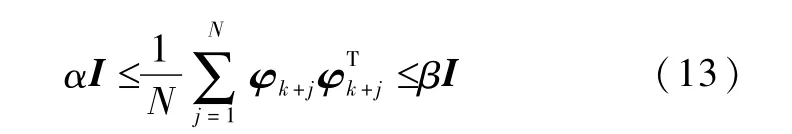
并且参数λ1和λ2满足下列条件
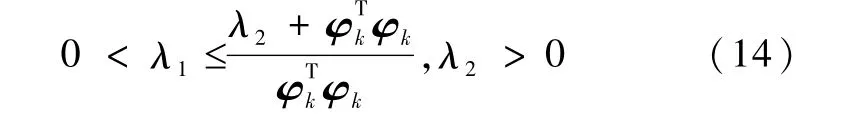
那么,下列不等式成立
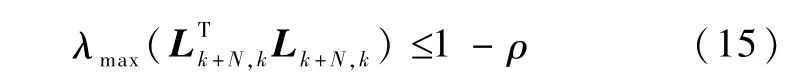
其中,符号λmax(·)表示矩阵的最大特征值,正常数ρ的取值如下所示
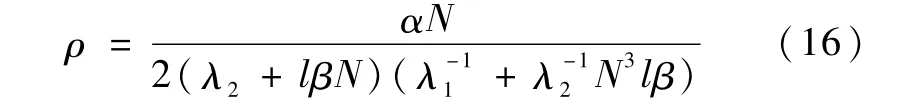
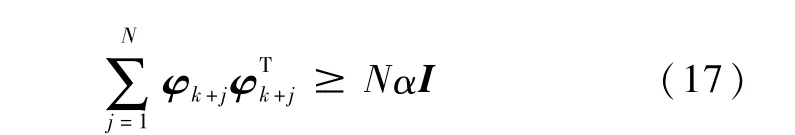
本文中矩阵不等式A≥B表示A-B≥0,即A-B为半正定矩阵.构造差分方程
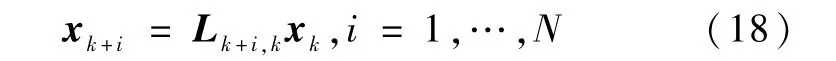
其中,xk是矩阵的最大特征值对应的单位特征向量,即xk使下式成立
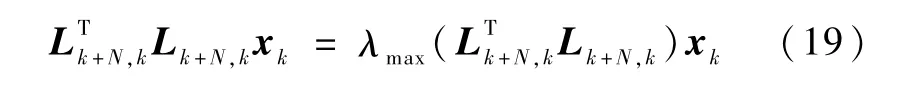
并且,

由式(17)和式(20)易知
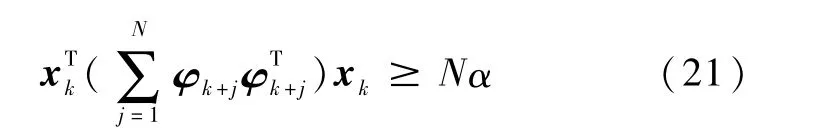
其次,由已知条件式(13)还可得到
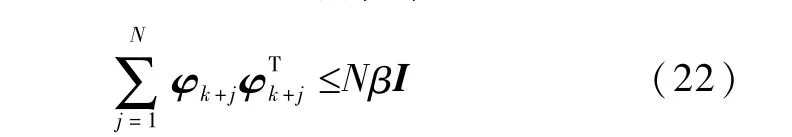
对上式两边取迹得
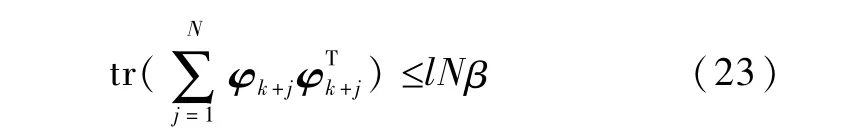
符号tr(·)表示取矩阵的迹.考虑到
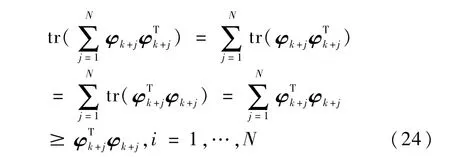
结合式(22)和(24)可得
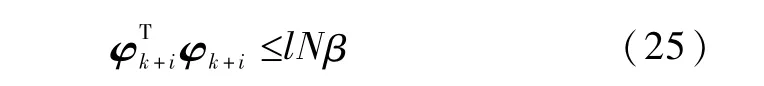
式(25)左右两边加λ2得到
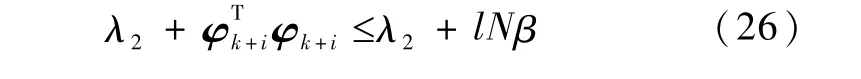
或
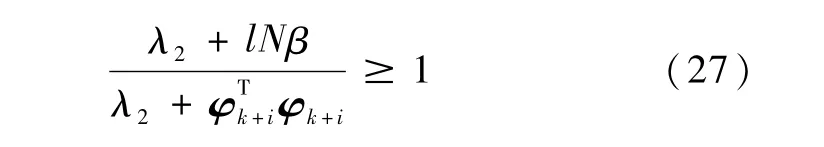
由式(27)和式(21)等号左边可写为
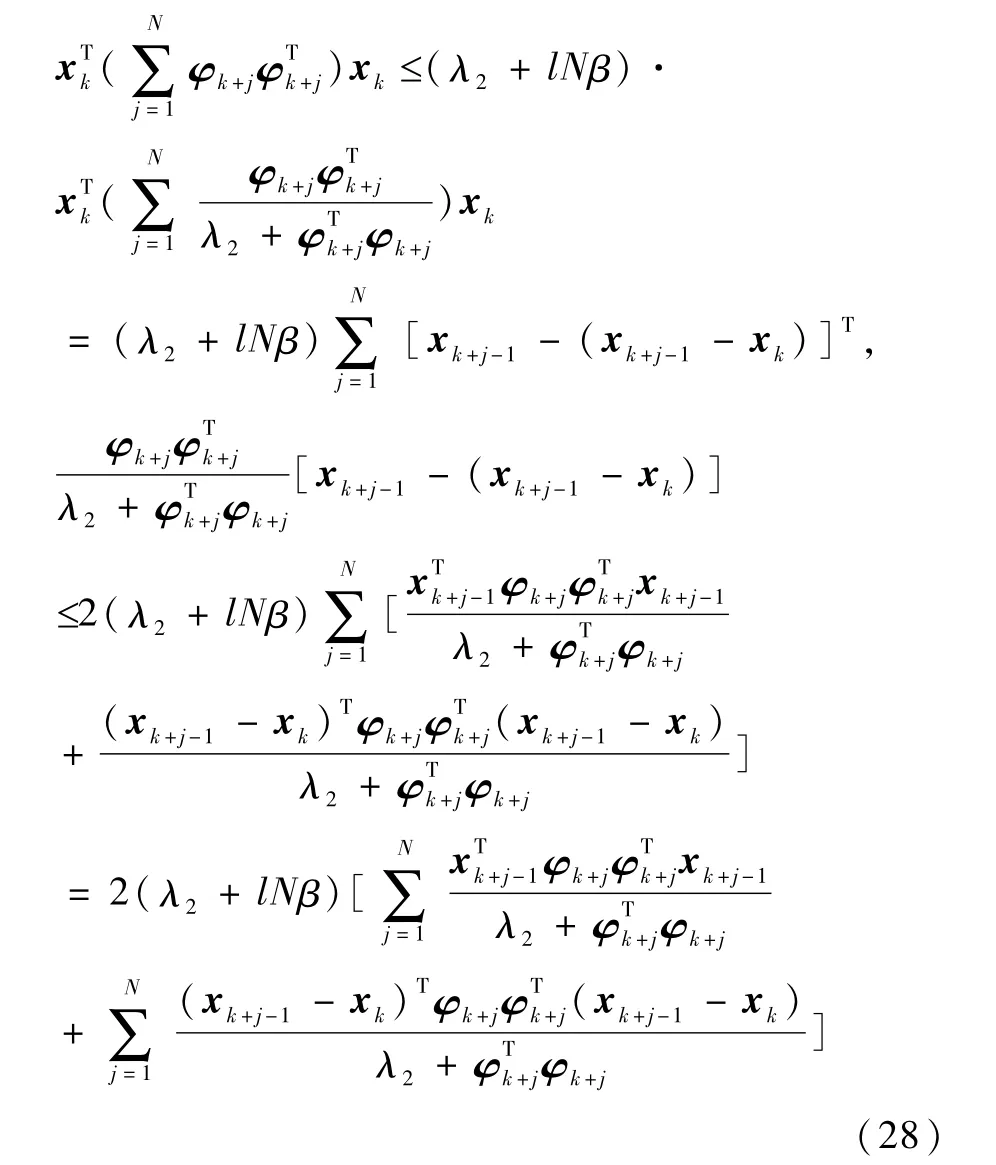
分别考察式(28)括号中的两项.先考察第 1项,由式(18)和式(11)可得
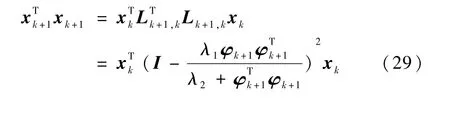
直接计算二者的差
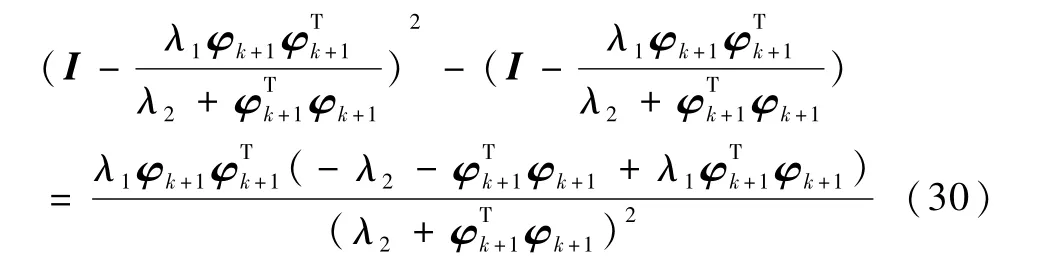
由假设条件式(14)易知
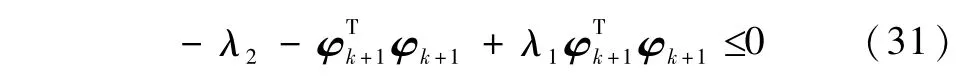
因此,
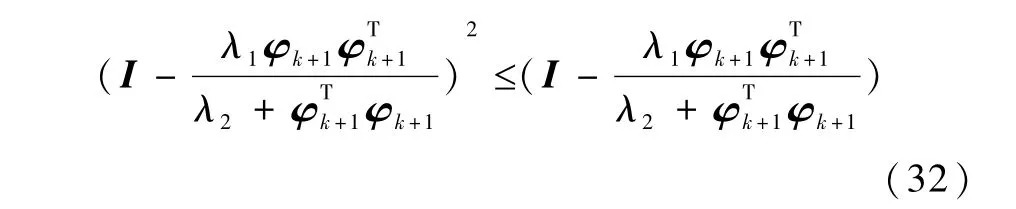
将式(32)代入式(29)得到
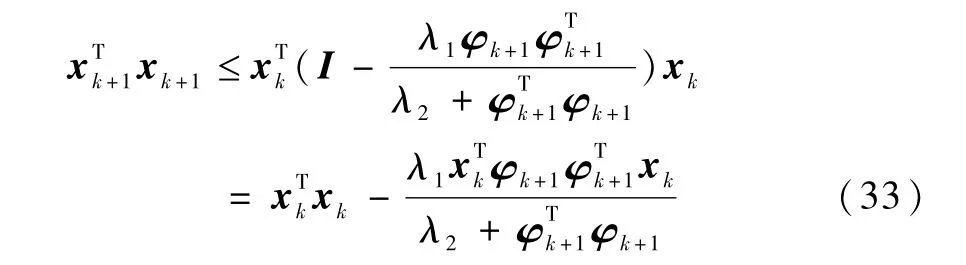
或
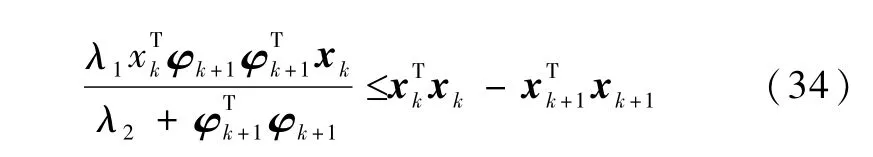
同理,

将以上各式相加,并由式(18)~(20)可知
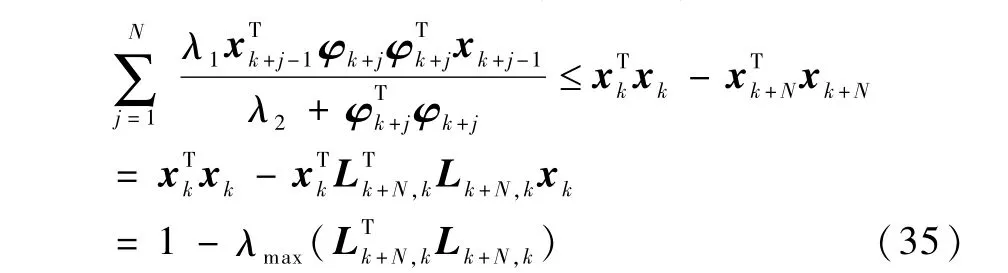
根据式(35)可得,式(28)括号中的第一项可写为再考察式(28)括号中的第二项
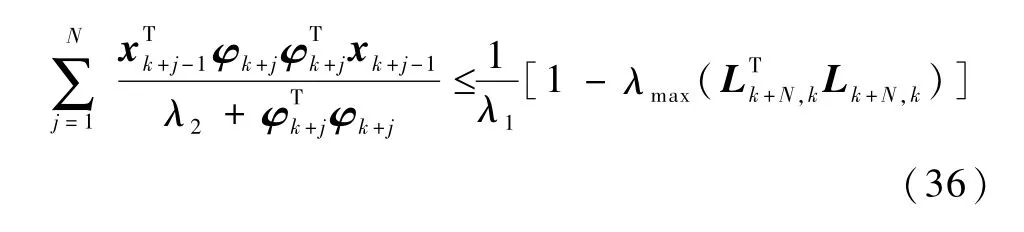
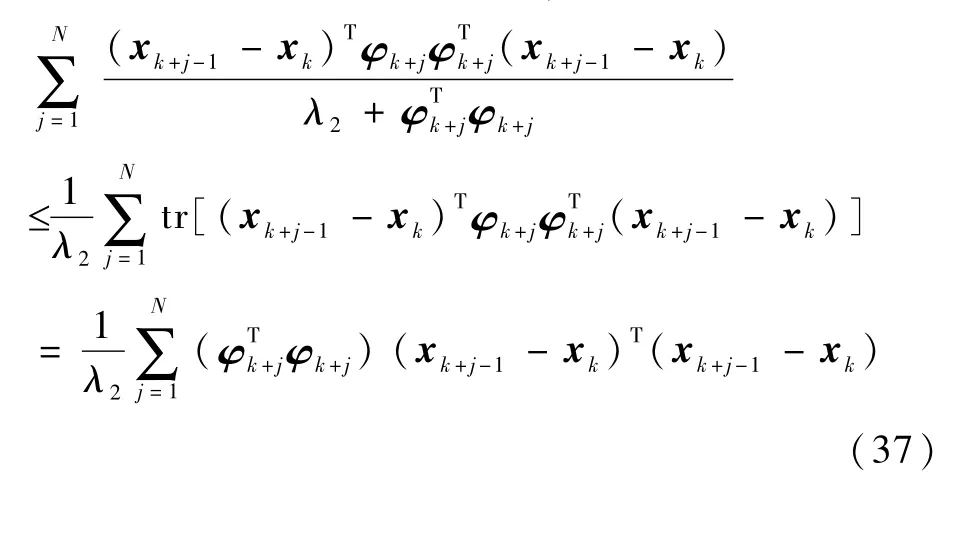
将式(25)代入式(37)可得
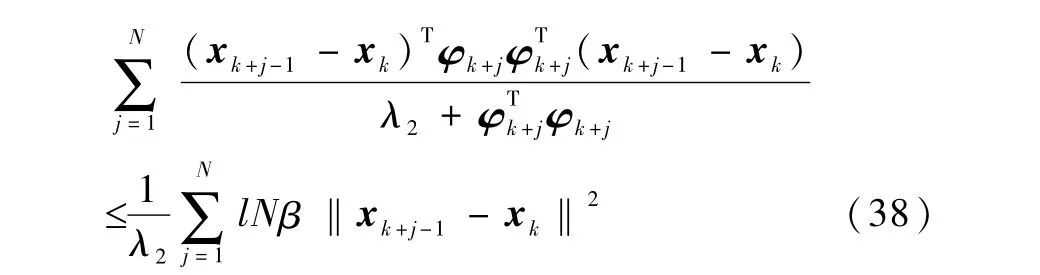
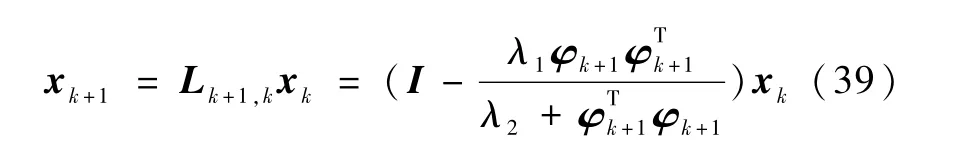
或
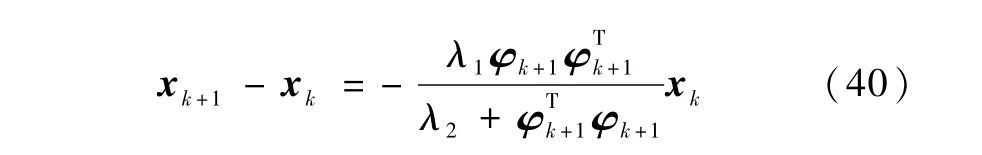
同理,
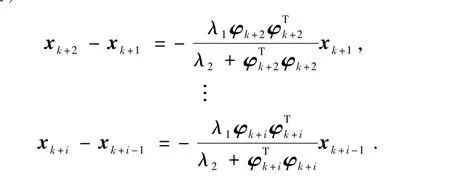
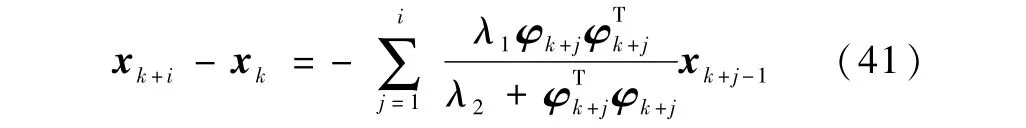
考察xk+i-xk的范数,由范数的性质和柯西不等式可得
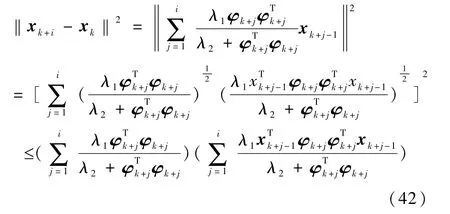
将以上各式相加可得
由假设条件式(14)易知
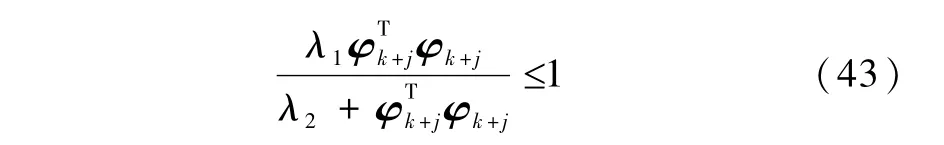
因此,
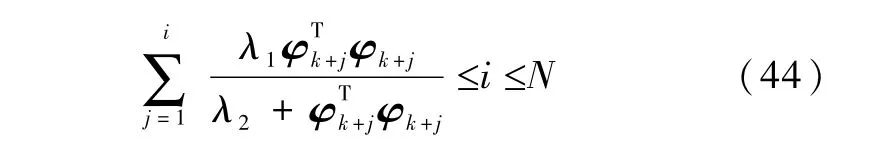
又由式(35)可知
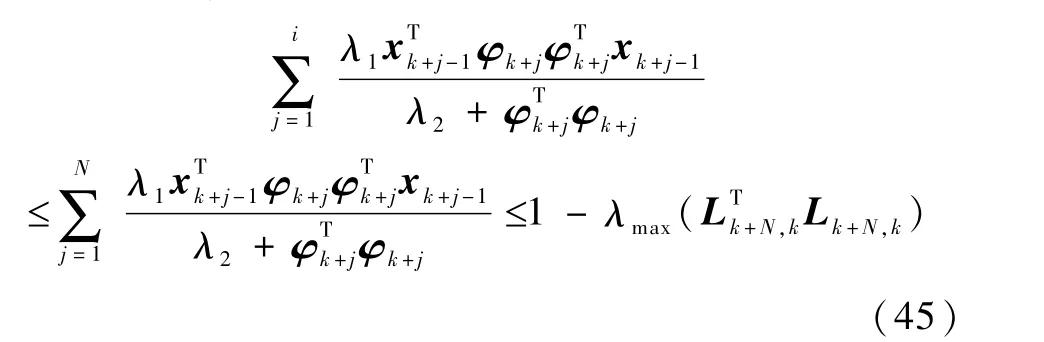
将式(45)和式(44)代入式(42)可得
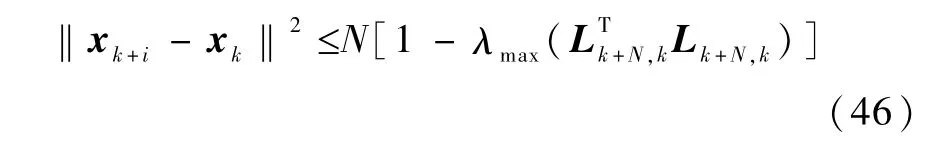
将式(46)代入式(38),式(28)括号中的第二项可写为
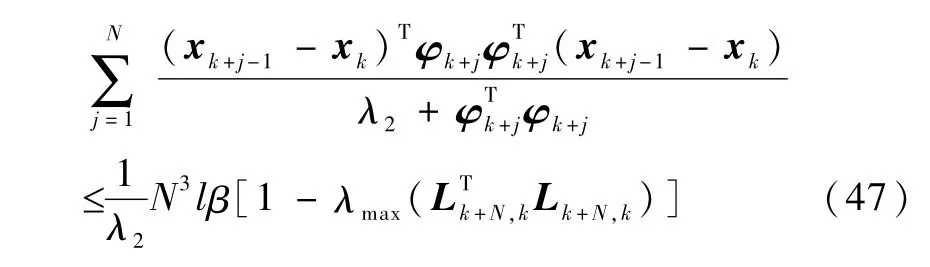
将式(36)和式(47)代入式(28),得到
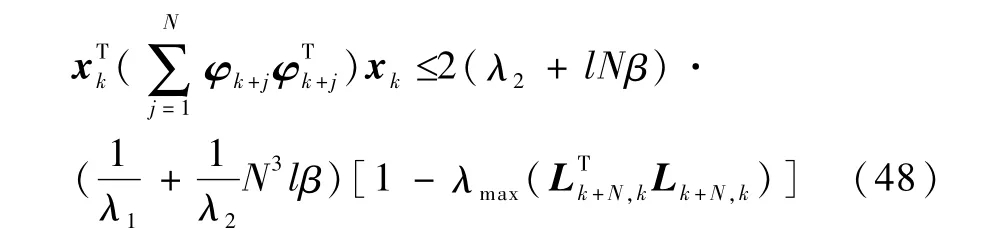
又由式(21)可知
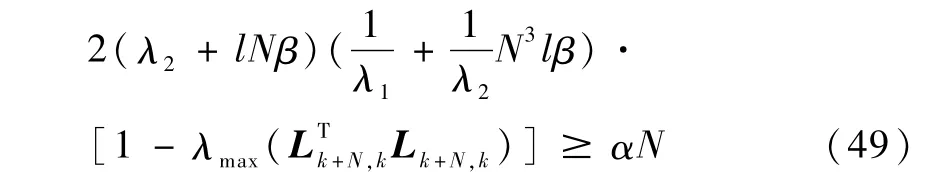
由式(49)可得引理2的结论.
引理2中的条件(13)通常被称为持续激励条件,该条件是引理2成立的关键,也是时变参数辨识梯度算法估计误差有界的充分条件之一.
4 稳定性分析
本节基于引理1和引理2对时变参数辨识梯度算法的稳定性进行分析,主要结果可归纳为如下定理.
定理1.考虑如式(1)和式(2)所示的系统和如式(5)所示的参数辨识梯度算法.如果存在正常数α、β、qmax、rmax、φmax和φmin,使得下列不等式成立
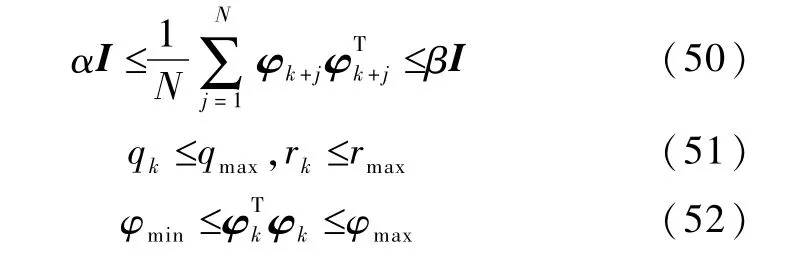
并且,梯度算法中的参数λ1和λ2满足
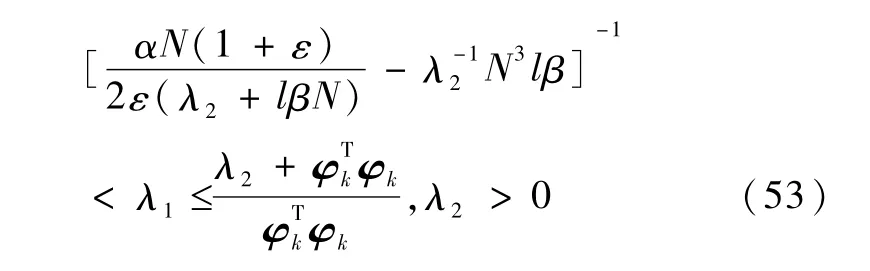
其中,
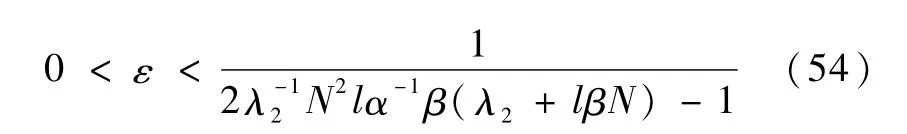
那么,参数估计误差ξt满足如下所示的有界性条件
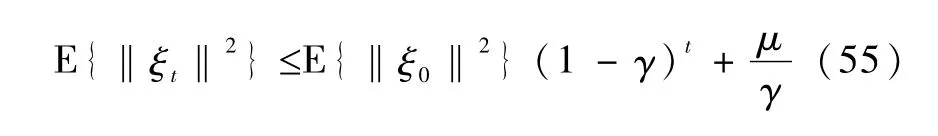
其中,
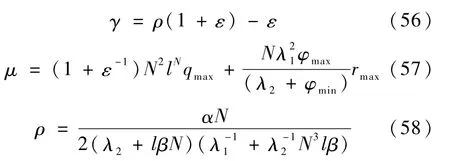
证明.定理1的证明围绕引理1中两个条件的验证进行,并需要用到引理2的结论.选择能量函数
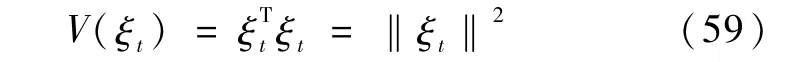
显然,对于vmax=vmin=1,引理1中的条件式(8)成立.下面根据假设条件验证引理1中的条件式(9).
由式(1)、(2)和(5),可得参数估计误差的表达式为
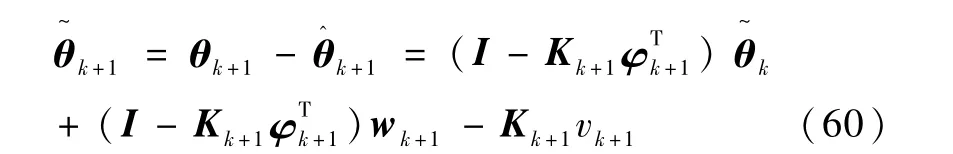
根据Lk+i,k的定义式(11)可得
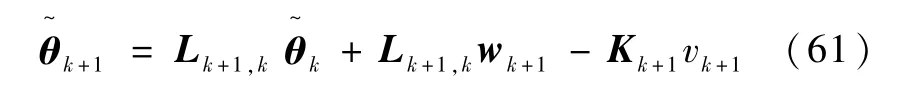
采用类似方法可得
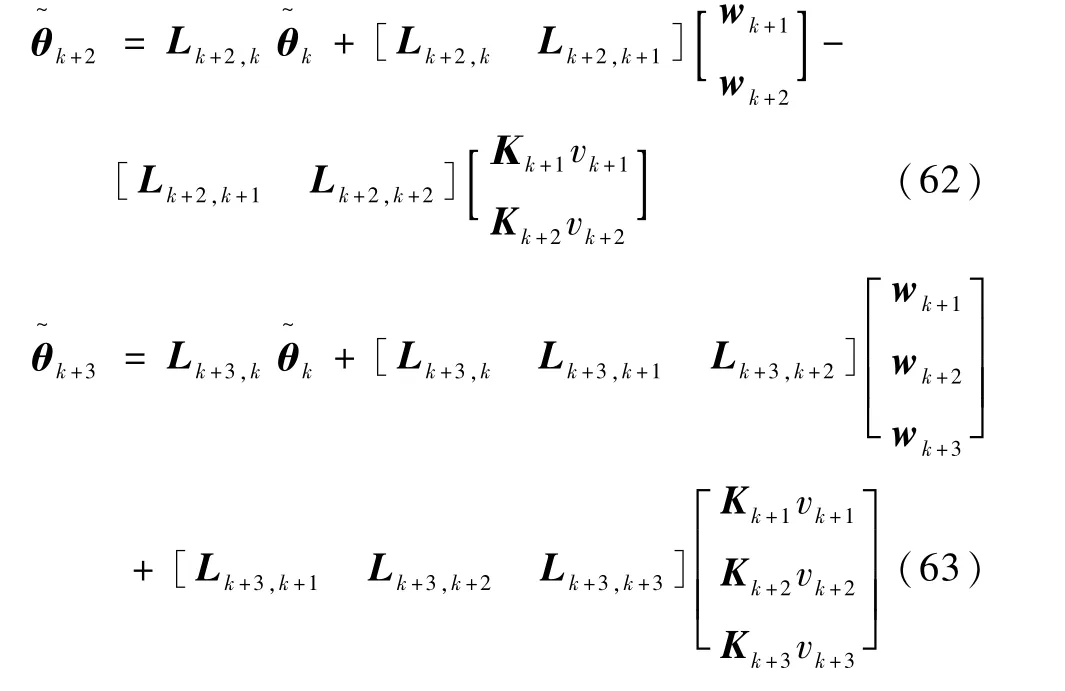
以此类推,得到
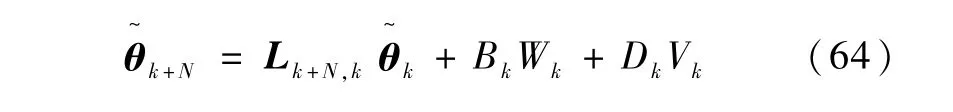
其中,
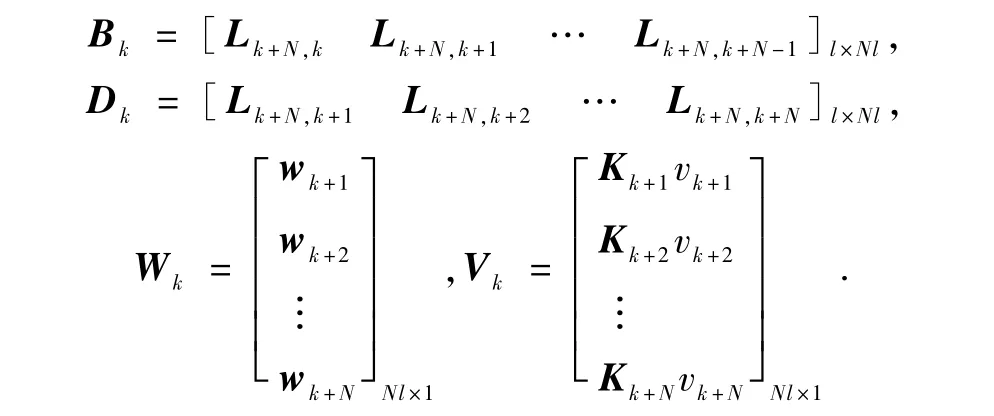
k=Nt时,参数估计误差可写为
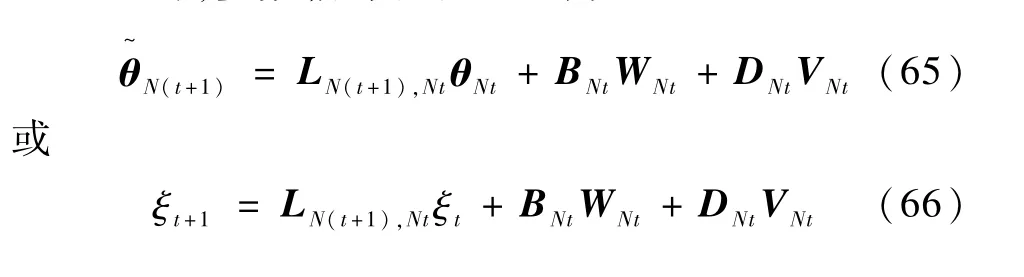
接下来,将式(66)代入式(59),并求能量函数V(ξt)的条件均值.
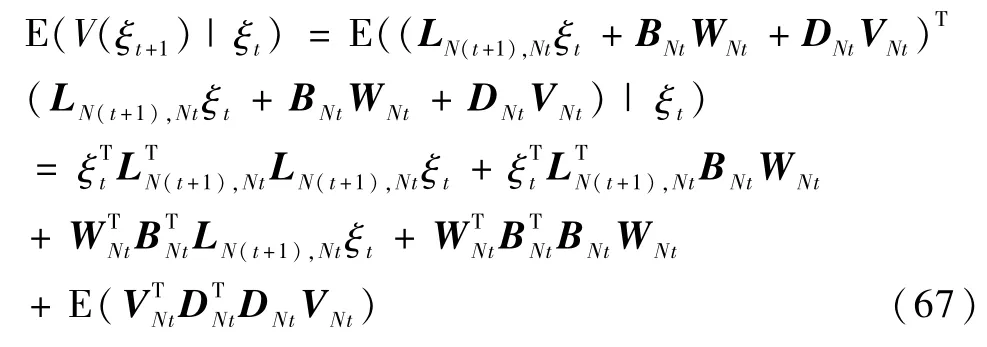
由不等式
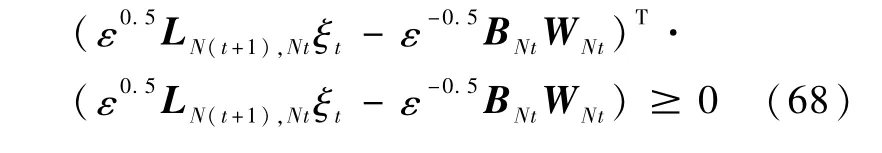
可得
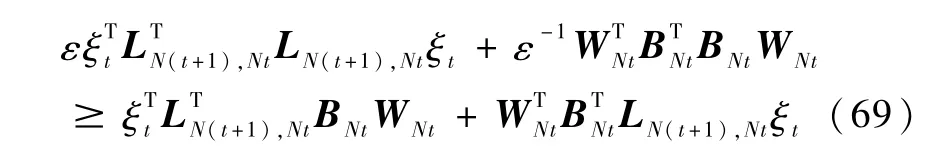
将式(69)代入式(67)可得
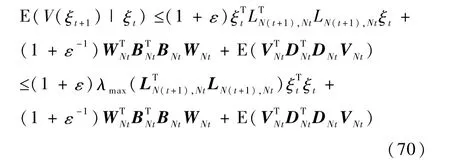
根据引理2的结论(15)可得
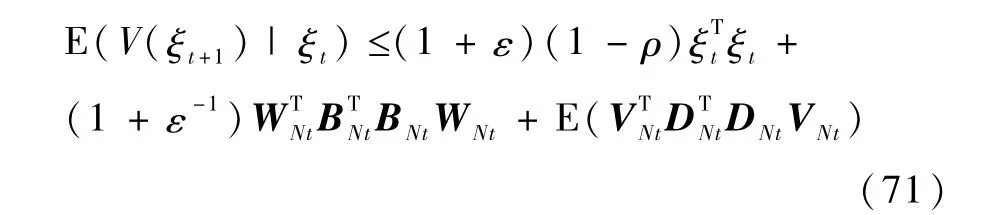
将式(71)两边减去能量函数V(ξt),得到与引理1中的式(9)相似的形式
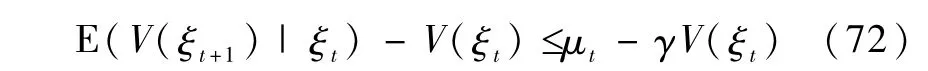
其中,γ如式(56)所示,
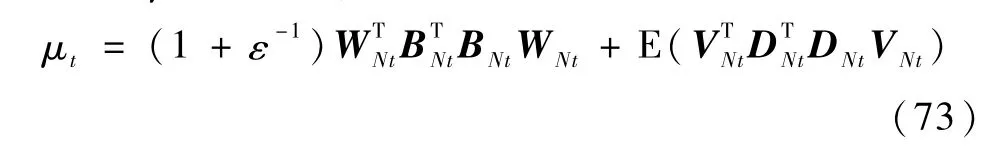
下面考察μt与μ的关系.先考察μt表达式(73)右边的第1项.
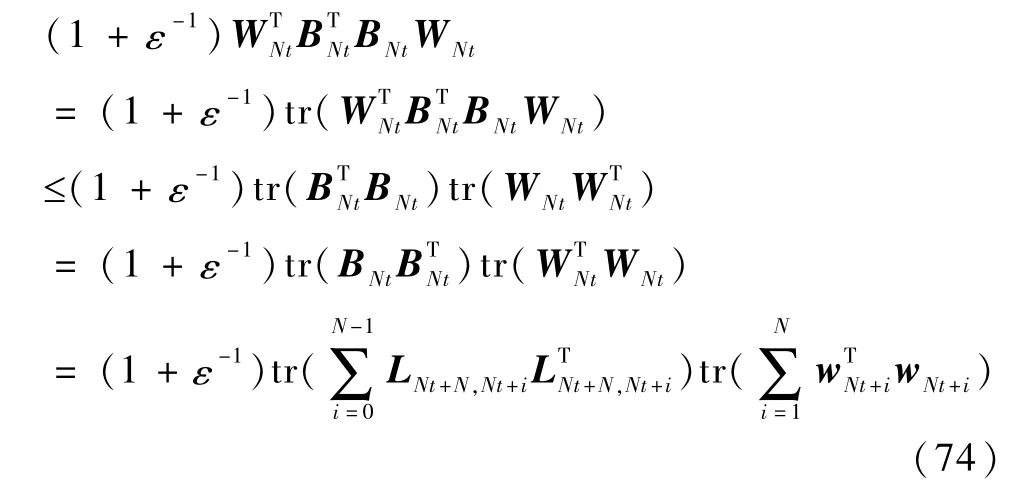
其中,
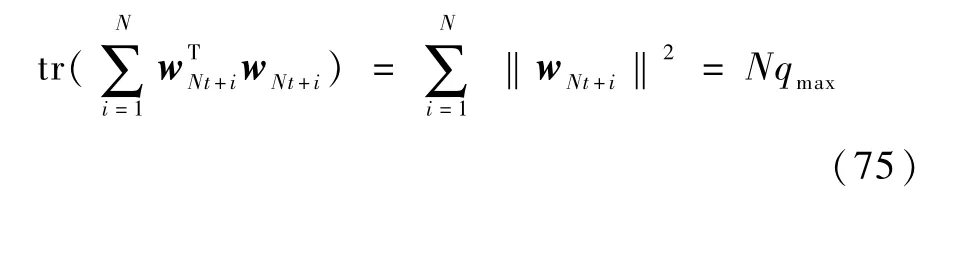
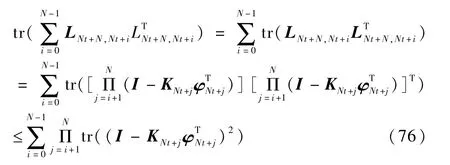
由式(32)可知
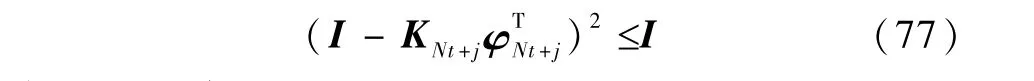
将式(77)代入式(76)得到
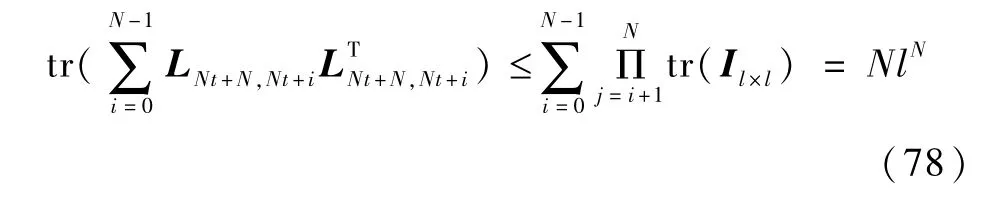
将式(78)和式(75)代入式(74)可得
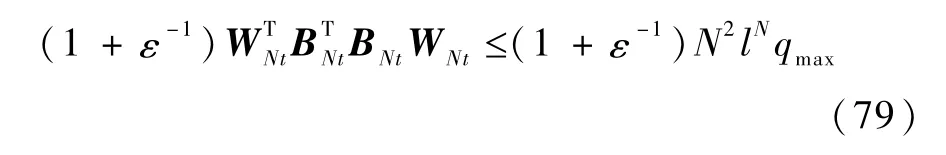
再考察μt表达式(73)右边的第2项.
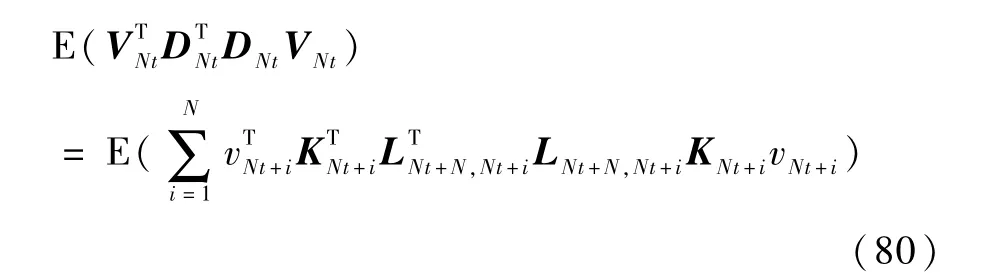
由式(77)可知
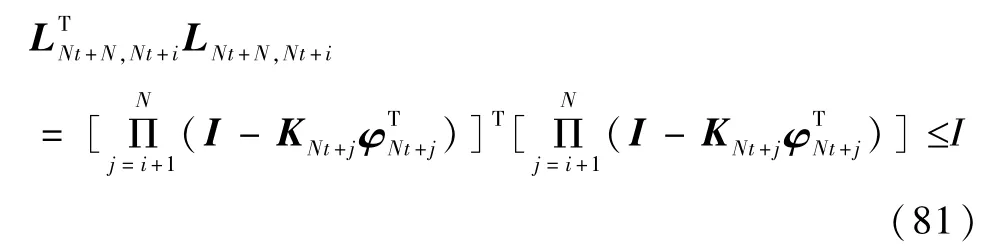
将式(81)代入式(80),并应用假设条件式(51)和式(52)可得
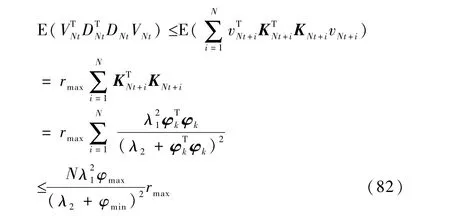
将式(82)和式(79)代入 μt表达式(73),与 μ的表达式(57)相比可得

显然,μ>0.
进而,考察γ的取值.由条件式(53)和式(54)可知
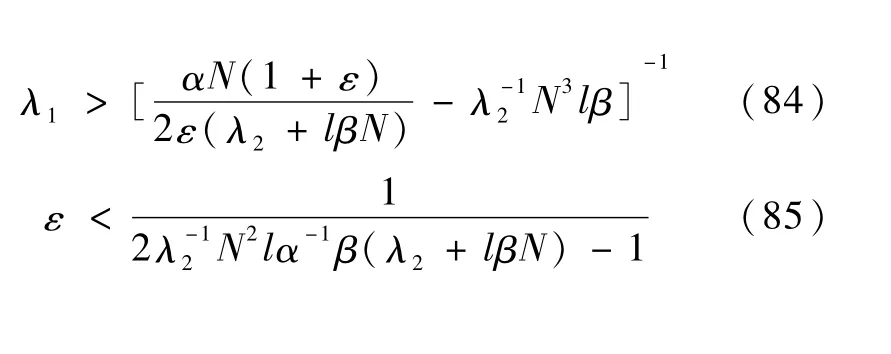

根据式(86)和γ的表达式(56)可知
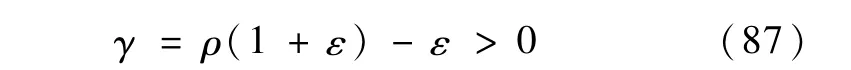
由引理2中的结论式(15)得
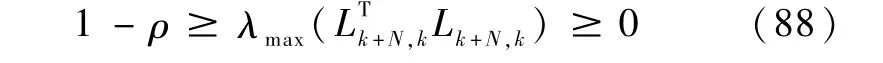
或

由等式
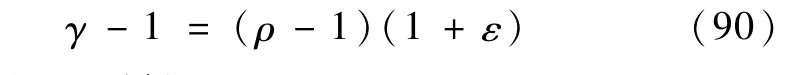
和不等式(89)可得

最后,由式(72)和式(83)可得,存在常数 μ>0,0<γ≤1,使得以下不等式成立,
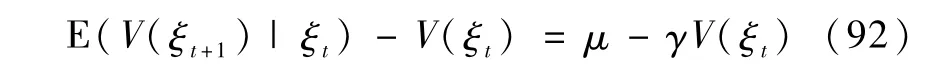
引理1中的条件式(8)和式(9)均得到验证,应用引理1可得定理1中的结论.
定理1表明,在时变参数辨识系统满足持续激励条件,且待辨识参数的变化率wk和测量噪声 vk方差有界的情况下,通过在参数辨识梯度算法中选择适当的参数λ1和λ2,能够确保估计误差ξt的有界性.通过定理1的结论式(55)和式(57)不难看出,随着在参数辨识梯度算法的迭代运行,其估计误差上界渐近的不受初始误差ξ0影响,估计误差上界的取值与参数变化率和测量噪声方差的上界qmax和rmax有关.特别是如果参数变化率和测量噪声方差均为0,那么梯度算法的估计误差 ξt将随着时间的推移(t→∞)收敛到0.将式(84)代入ρ的表达式(58),并应用式(85),易于验证
5 结 论
本文对一种辨识算法-时变参数辨识梯度算法进行了稳定性分析.基于随机过程有界性判据,给出了时变参数辨识梯度算法稳定的充分条件.结果表明,在待辨识参数变化率有界,观测噪声是零均值白噪声,且系统满足持续激励条件的情况下,通过在参数辨识梯度算法中选择适当的参数,能够确保参数估计误差的有界性.并且,对于确定性时不变系统,梯度算法的参数估计误差收敛,即误差随时间增长趋近于0.以上工作有望对特征模型时变参数辨识算法稳定性问题的研究起到促进作用.
[1] 丁锋,杨慧中,纪志成.时变系统辨识方法及其收敛定理[J].江南大学学报(自然科学版),2006,5(1): 115-126 Ding F,Yang H Z,Ji Z C.Time-varying system identification methods and convergence theorems[J].Journal of Southern Yangtze University(Natural Science Edition),2006,5(1):115-126
[2] 陈增强,林茂琼,袁著祉.递推阻尼最小二乘的收敛性与稳定性[J].应用数学和力学,2000,21(2):209-214 Chen Z Q,Lin M Q,Yuan Z Z.Convergence and stability of recursive damped least square algorithm[J].Applied Mathematics and Mechanics,2000,21(2):209-214
[3] 吴宏鑫,胡军,解永春,基于特征模型的智能自适应控制[M].中国科学技术出版社,2009 Wu H X,Hu J,Xie Y C.Characteristic model-based intelligent adaptive control[M].China Science and Technology Press,2009
[4] Reif K,Gunther S,Yaz E,et al.Stochastic stability of the discrete-time extended Kalman filter[J].IEEE Transactions on Automatic Control,1999,44(4):714-728
[5] Xiong K,Zhang H Y,Chan CW.Performance evaluation of UKF-based nonlinear filtering[J].Automatica,2006,42:261-270
[6] Xiong K,Liu L,Liu Y.Nonlinear robust filter design for satellite attitude determination[J].IET Control Theory&Applications,2010,4(7):1222-1234
[7] 丁锋,丁韬,杨家本,等,时变参数遗忘梯度估计算法的收敛性[J].自动化学报,2002,8(6):962-968 Ding F,Ding T,Yang J B,et al.Convergence of forgetting gradient estimation algorithm for time-varying parameters[J].Acta Automatica Sinica,2002,8(6):962-968
Stability Analysis of Tim e-Varying Param eter Identification G radient A lgorithm
XIONG Kai1,2,MENG Bin1,2,WANG Lijiao1,2
(1.Beijing Institute of Control Engineering,Beijing 100190,China; 2.Science and Technology on Space Intelligent Control Laboratory,Beijing 100190,China)
The stability of a gradient algorithm for time-varying parameter identification is studied in this paper.The stability of the time-varying parameter identification gradient algorithm is analyzed by using the stochastic process boundedness criterion.The sufficient conditions to ensure the stability of the gradient algorithm are demonstrated.It is shown that if the rate of variation of the parameter to be identified is bounded,and themeasurement noise is zero-mean white noise,under the persistent excitation condition,the identification error given by the properly designed gradient algorithm is bounded in the sence ofmean square.This analysis is different from prior works in that it is not necessary to assume that the parameter variation is the zero-mean white noise in the proof of the theory.
parameter identification;gradient algorithm;stochastic process;stability
V4
A
1674-1579(2012)05-0014-07
熊 凯(1976—),男,高级工程师,研究方向为非线性滤波和航天器自主导航.孟 斌(1973—),女,高级工程师,研究方向为自适应控制、奇异控制、航空航天控制;王丽娇(1986—),女,博士研究生,研究方向为航天器自适应控制.
*国家自然科学基金资助项目(61074103).
2012-03-08
DO I:10.3969/j.issn.1674-1579.2012.05.003
