一种计算碰撞概率的分析解
2012-09-05林彦
林 彦
(中国航天科工卫星技术有限公司,北京100071)
一种计算碰撞概率的分析解
林 彦
(中国航天科工卫星技术有限公司,北京100071)
碰撞概率的大小表征航天器相遇过程的危险程度,碰撞概率是航天器规避机动策略制定的参考依据.如果两个飞行器的相对速度很大且相遇过程很短,相对运动可近似为线性运动,这样就可以将三维概率求解问题转化为二维概率问题.这类的碰撞概率求解通常应用数值计算方法.基于概率积分推导一种碰撞概率计算的分析解,能有效降低计算量并不损失太多精度.最终给出模拟算例验证分析解的准确性.
碰撞概率;航天器;概率积分
碰撞概率的大小表征了航天器相遇过程的危险程度,是航天器规避机动策略制定的参考依据.如果飞行器与空间碎片的相对速度很大、相遇过程很短,相对运动可近似为线性运动,这样就可以将三维概率求解问题转化为二维概率问题.这种情况下的碰撞概率求解即为计算两个航天器(或空间碎片)相遇过程中最小距离进入等效组合包络体的概率.对于二维相遇过程的碰撞概率计算方法研究,Patera[1]使用一维路径积分方法替代二维面积积分,从而提高计算速度,还把相遇航天器的类型从对称体推广到非对称体;Patera[2]通过把一维路径积分坐标系的原点从组合包络体的中心转换为概率密度圆的中心,从而简化积分表达式.如果相对运动速度很慢且运动轨迹较为复杂,线性相对运动方法不再适用,Patera[3]开发了非线性运动情况下的三维碰撞概率计算方法,把碰撞概率计算从高速相遇过程推广到低速相对运动;McKinley[4]对三维碰撞概率计算方法给出详细的数值积分过程,并获得了与文献[3]类似的求解精度,白显宗等[5]使用无穷级数方法来提高碰撞概率计算的快速性.上述方法通常需要的求解精度都以大量的数值积分为代价,不可避免地耗费大量的求解时间,为此本文基于概率积分的计算推导了一种碰撞概率的分析解,能有效降低计算量并不损失太多精度.本文首先描述线性相遇运动下的碰撞概率计算问题,然后阐述基于概率积分的碰撞概率计算方法并推导计算公式,最终给出模拟算例来验证方法的准确性.这里定义被预测航天器为目标航天器,具备预警能力的航天器为参考航天器.
1 线性碰撞概率计算方法
1.1 假设条件
碰撞概率计算方法通常基于以下假设[1-5]:(1)能够获得两个航天器最接近时刻在惯性系中的位置、速度和位置误差矩阵;(2)两个航天器的外形建模为包络球或其它简单几何体的组合;(3)通常把空间两个航天器的相对位置误差分布视为三维高斯分布,如果两个航天器的绝对状态协方差矩阵不相关,则其和就是相对状态的协方差矩阵.如果航天器的外形建模为包络球,则两个航天器的包络球合并为一个总包络球,其半径大小等于两个单独的包络球之和.(4)把所有随机因素赋予参考航天器.相对状态误差分布的中心设置在参考航天器.
1.2 坐标系定义
当两个航天器在三维空间内的距离达到最小时,它们的相对位置矢量和相对速度矢量互相垂直.或者说,当两目标间的距离最近时,它们处在与相对速度矢量垂直的平面内.为了便于描述问题,这个平面通常定义为相遇平面.把两物体的位置不确定性包络球投影到相遇平面上,求解碰撞概率的3维积分从而简化为二维积分.参见图1所示.据此定义相遇坐标系:原点O在参考航天器的分布中心,z轴指向相对速度方向,χ轴和y轴在相遇平面内,χ轴指向的目标航天器的分布中心在相遇平面内的投影点,y轴在相遇平面内与χ轴垂直.

图1 相遇平面和积分区域Fig.1 Encountering plane and integral region
1.3 求解方法
三维空间内等方差概率密度函数的碰撞概率定义为[2]

如果相对运动可视为线性运动,则仅需对二维等方差概率密度函数进行积分.碰撞概率简化为

式中,S描述了总包络体几何位置和尺寸.
对于一般性的线性运动碰撞概率问题,若要应用式(1)~(2),如果被积分函数是不等方差概率密度函数,即 σχ≠σy,通常还需要应用变量代换[2,5]的方法;如果概率密度椭圆的对称轴与坐标系不重合,需要通过坐标转换方法[1-2]来对齐.
2 分析解
为导出分析解,在图1所示部分上构造图2所示的4个积分区域.设总包络体投影为圆形,则有: S1:χ2+y2≤ (b-r)2,S2:χ2+y2≤ (b+r)2,S3:(χ-b)2+y2≤ r2,S4为部分圆环,即图 2中角∠AOB定义为β,即β=2arcsin(r/b).

图2 积分区域与圆环关系Fig.2 Relation between the integral region and the ring
根据概率积分的一般理论可知,对圆心在原点的圆域的概率积分有以下分析解[6]:

由式(3)可知,容易计算 S1、S2区域的碰撞概率.S4区域属于S1、S2之间圆环的部分区域,根据对称性可知对于S4区域的碰撞概率为:
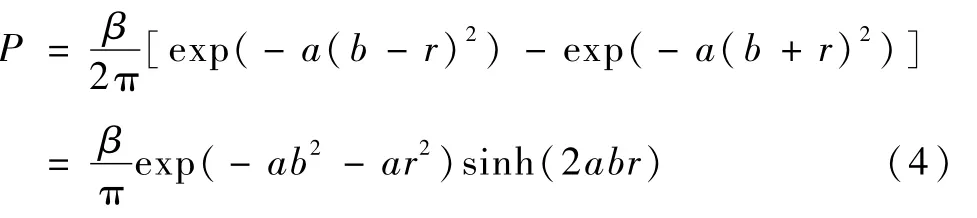
由于被积分函数都为正值,且 S4的面积包含S3,所以显然S4的碰撞概率大于S3的值.为了提高近似程度,需进行修正.假设S4、S3的概率密度均匀且相等,则修正系数取两者面积比值的倒数:

对式(4)应用修正系数可得S3圆域的碰撞概率近似值的分析解:

3 模拟计算
计算条件:
1)两个航天器的最小距离取:b=10km;
2)总包络球的半径尺寸(RCS)取值范围: 10m≤r≤100m;
3)概率密度函数的方差取值:σ=3km,5km,9km;
4)数值解法取文献[2]的式(10),解记为Q.

图3 不同尺寸的碰撞概率对比(σ=3km)Fig.3 Comparison of the collision probability of the rigid bodies with different size(σ=3km)
4 结 论
碰撞概率的计算方法通常都对积分方法有较高的要求,以大量的数值积分为代价来保证求解精度.数值计算不可避免的要耗费大量的求解时间和降低可使用性.按照本文基于概率积分提出的碰撞概率的分析解,能有效降低计算量并不损失太多精度.本文描述的求解方法对总包络体的外形没有过高的要求,容易把本方法推广到任意外形的情况.

图4 不同尺寸的碰撞概率对比(σ=5km)Fig.4 Comparison of the collision probability of the rigid bodies with different size(σ=5km)
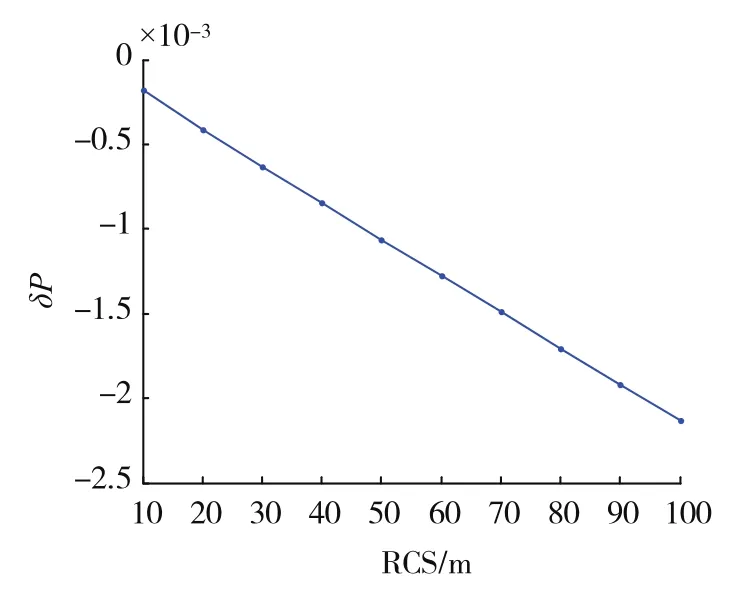
图5 不同尺寸的碰撞概率对比(σ=9km)Fig.5 Comparison of the collision probability of the rigid bodies with different size(σ=9km)
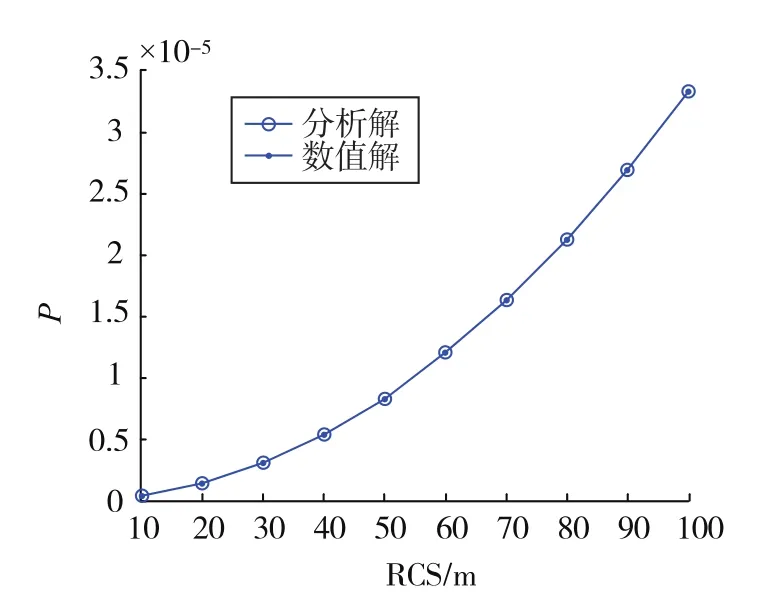
图6 两种计算方法的碰撞概率对比(σ=9km) Fig.6 Comparison of two algorithms
[1] Patera R P.Generalmethod for calculating satellite collision probability[J].Journal of Guidance,Control,and Dynam ics,2001,24(4):716-722
[2] Patera R P.Calculating collision probability for arbitrary space-vehicle shapes via numerical quadrature[J]. Journal of Guidance,Control,and Dynam ics,2005,28 (6):1326-1328
[3] Patera R P.Satellite collision probability for nonlinear relativemotion[J].Journal of Guidance,Control,and Dynamics,2003,26(5):728-733
[4] McKinley D P.Development of a nonlinear probability of collision tool for the Earth observing system[R]. AIAA,2006-6295
[5] 白显宗,陈磊.基于空间压缩和无穷级数的空间碎片碰撞概率快速算法[J].应用数学学报,2009,32 (2):336-353 Bai X Z,Chen L.A rapid algorithm of space debris collision probability based on space compression and infinite series[J].Acta Mathematicae Applicate Sinica,2009,32(2):336-353
[6] 李银奎.概率积分的几种计算方法[J].青海师专学报,2002,22(5):22-23 Li Y K.Several calculated methods of the probability integral[J].Journal of Qinghai Junior Teachers'College(Natural Science Edition),2002,22(5):22-23
Analytical Solution for Collision Probability Calculation
LIN Yan
(CASIC Satellite Technology Ltd.,Beijing 100071,China)
Collision probability represents the risk of collision between two spacecrafts during the encountering phase.Collision probability calculation is the basis of designing the collision avoidance maneuver strategy.If the relative velocity between two spacecrafts is large and the encountering time is short,the relative motion is approximately linear.Under this assumption,the problem of solving the three-dimensional probability density is reduced to a two-dimensional problem.Numerical integralmethods are usually used to calculate the collision probability.An analytical solution based on probability integral is derived,which can reduce the amount of computation while the decreased accuracy is not so much.A case study is presented to validate the given method.
collision probability;spacecraft;probability integral
V448
A
1674-1579(2012)06-0041-04
10.3969/j.issn.1674-1579.2012.06.009
林 彦(1976—),男,高级工程师,研究方向为航天器总体设计.
2012-10-15
