一种具有饱和积分项的卫星姿态控制律

胡锦昌，张洪华

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

一种具有饱和积分项的卫星姿态控制律

胡锦昌1，2，张洪华1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

为消除常值干扰的影响，提出了一种具有饱和积分项的类PID姿态控制律.所提出的控制律不仅可以消除常值干扰带来的影响，并且由于积分项具有饱和约束，该控制律可以防止控制量由于积分项的持续积分而变得过大.利用前向系统的相关理论，严格证明了闭环系统的全局渐近稳定性质，并给出了相应的充分条件.仿真验证了该方法的有效性.

姿态控制;类PID控制;饱和控制;前向系统

卫星姿态控制问题在过去的几十年里已经得到了大量的研究.文献[1]已经证明PD控制可以使得无干扰下的刚体卫星姿态得到稳定.在存在常值干扰的情况下，可以类似线性系统一样采用PID控制器来消除常值干扰的影响，此时的积分是指代表姿态角信息的某种参数的积分.但是，由于刚体卫星姿态系统的非线性特征，要对一个PID控制的闭环姿态系统证明稳定性是非常困难的.目前关于卫星非线性姿态系统的 PID控制的文献还不多，如文献[2-6].文献[2]给出了一种基于修正Rodrigues参数的类PID的控制律;文献[3]给出了一种含有四元数和角速度组合积分形式的 PID控制律;文献[4]基于四元数提出了一种需要抵消陀螺力矩项的类PID控制律;文献[5]则提出了一种不需要知道角速度信息的PI形式的控制律.但是，文献[2-5]中的控制律或者其反馈系数和状态变量有关，或者需要抵消陀螺力矩项，因此它们给出的都还不是线性PID形式的控制律.文献[6]给出了一种基于拉格朗日形式的线性PID控制律，但是只能获得局部渐近稳定的性能.

众所周知，由于积分项的存在，控制量容易变得过大从而发生饱和，此时一般难以保证闭环系统的稳定性.为降低饱和对系统的影响，可以在积分项前加上饱和约束，如文献[7]，但是这样的话就难以证明闭环系统的稳定性.为克服此问题，本文提出一种新的具有饱和积分项的控制律，其中的积分项是四元数与角速度的线性组合.基于前向系统的相关理论[8]，本文从理论上证明了闭环系统的全局渐近稳定性质，并由此给出了相应的参数充分条件.

1 问题描述与定义

考虑刚体卫星的姿态稳定问题.存在常值干扰下的刚体卫星的姿态运动与动力学方程为

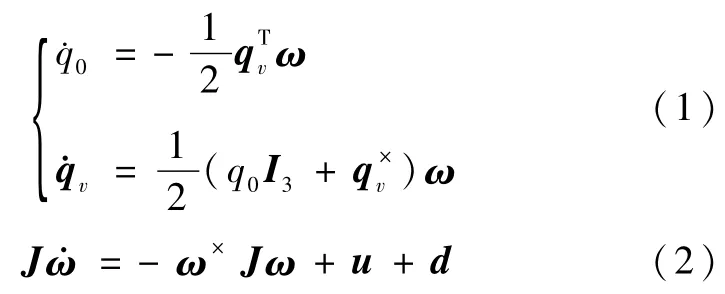
其中q=(q0，qυ)∈R×R3表示卫星的姿态四元数，q0和 qν分别表示四元数的标量与矢量部分;ω= (ω1，ω2，ω3)∈R3表示卫星相对于惯性系的角速度，并且在本体系表达;u∈R3表示控制力矩; d∈R3表示未知常值干扰;J∈R3×3为惯量阵;对∀ν∈R3，ν×表示作用于矢量 ν上的运算符，其结果为如下形式的反对称阵:

假设1:惯量阵 J精确已知，并且四元数(q0，qυ)与角速度ω均可以由测量而得.

假设2:常值干扰 d未知，但其上界已知，即存在已知正数dm，使得‖d‖∞≤dm.

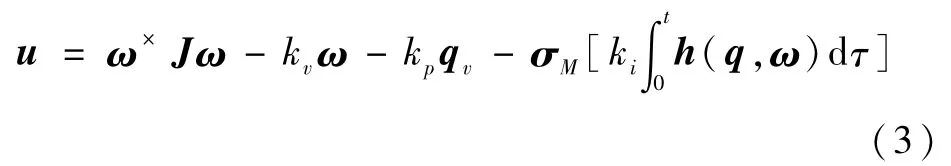
基于假设1和2，对式(1)、(2)表示的姿态方程，设计如下形式的控制律:其中kp，ki，kυ＞0分别为相应的PID系数;σM(·): R3→ R3为饱和函数，其定义为:∀s∈ R3，(σM(s))i=sgn(si)m in{M，|si|}，i=1，2，3，M＞dm;h(q，ω)为被积分项，其表达式为

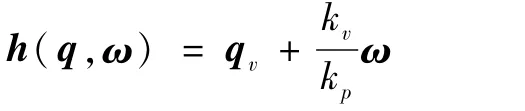
注1.在式(3)所表示的控制律中，第一项的作用是抵消掉陀螺力矩项，第二项与第三项分别是速率与比例项，最后一项则是具有饱和约束的积分项.

将式(3)所表示的控制律代入式(1)与(2)，可得闭环系统为

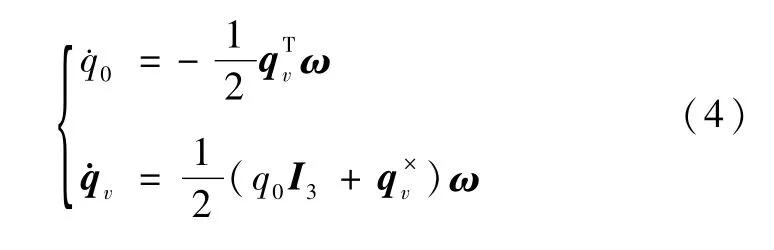
符号定义:在本文中，设惯量阵 J的诱导2范数为γJ，最小特征值为λmin，J.

2 稳定性分析

为方便闭环系统的稳定性分析，假设d=0.为利用前向系统的相关理论证明闭环系统的稳定性[8]，注意到当干扰和积分均等于零时，(q，ω)子系统是渐近稳定的[1].为此定义

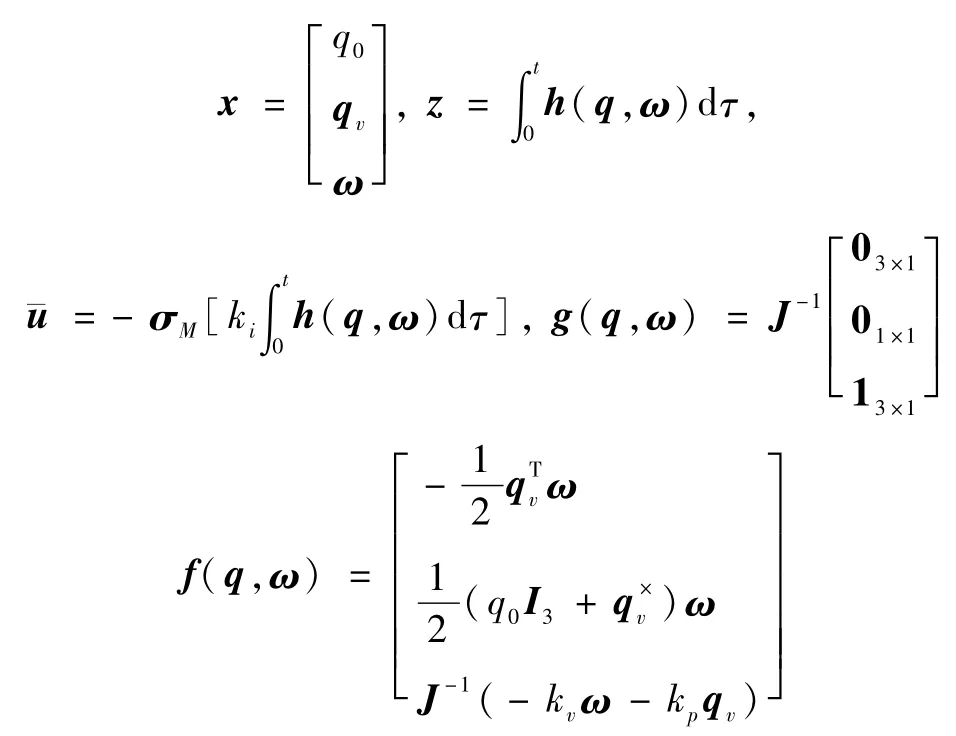
并将式(4)与式(5)写成如下形式:

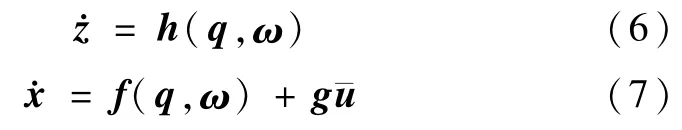
根据文献[1]，构造x子系统的Lyapunov函数为

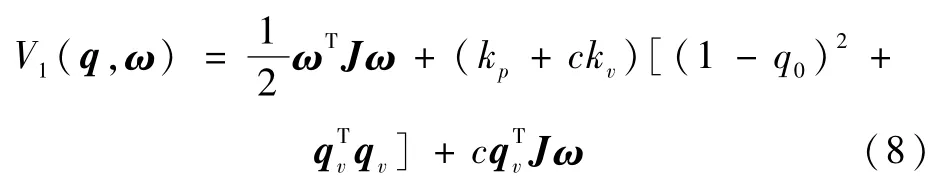
其中c为充分小的正数以使得V1(q，ω)正定.将V1沿式(7)对时间求导，可得:

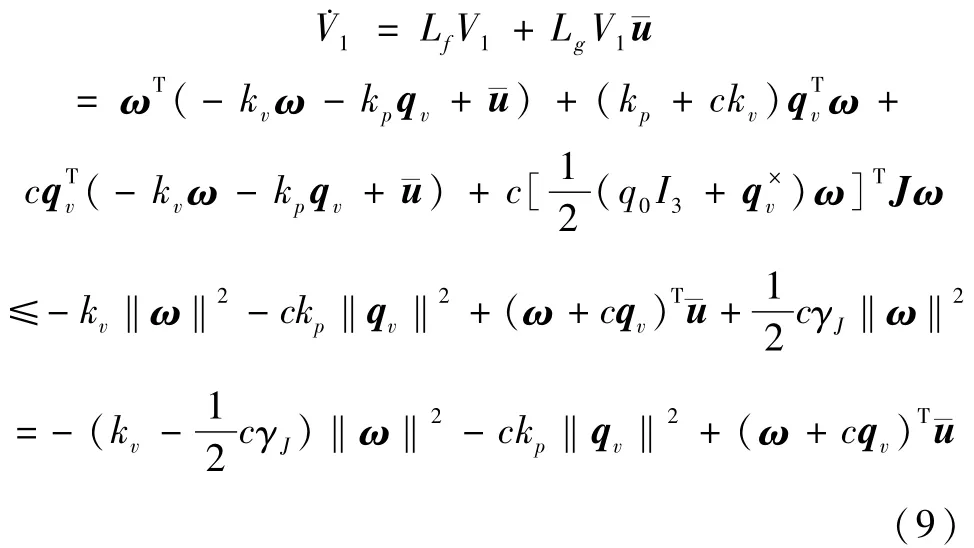
其中利用了‖q0I3+q×υ‖2=1，LfV1和LgV1表示分别求取V1沿f和g的Lie导数，后同.由式(9)可知:

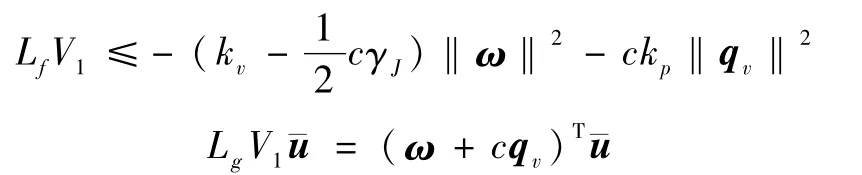
为使LfV1负定，需要满足如下条件:

根据V1(q，ω)，构造式(6)与(7)的总的Lyapunov函数为

其中φ＞0为充分大的正数，ψ(q，ω)为关于 (q，ω)的3维向量函数，其表达式为

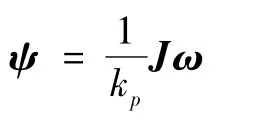
由上式可见ψ(q，ω)实际上仅为ω的函数.

注意到:

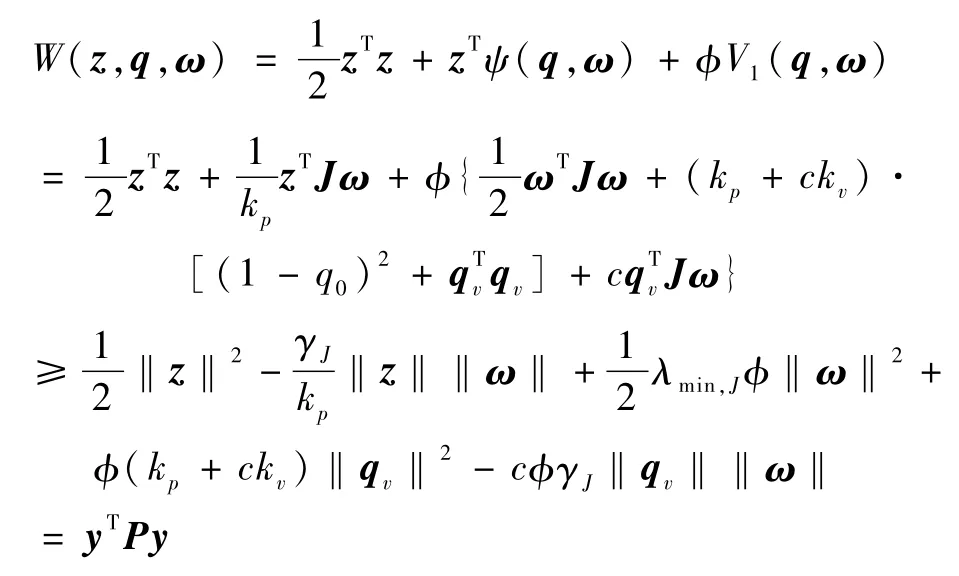
其中:

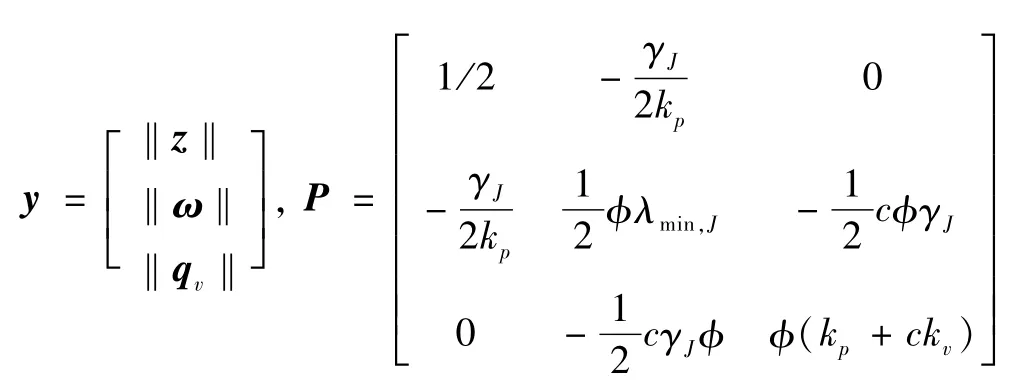
可见，为保证 W(z，q，ω)的正定性，只需保证矩阵P的正定性.可以验证，P的正定性可以通过选择充分大的φ和充分小的c实现.

容易证明

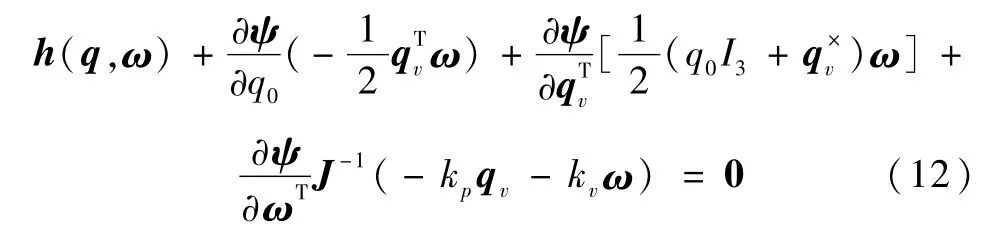
即有

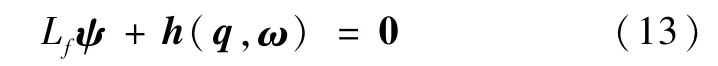
且有Lgψ=I3/kp.

将W(z，q，ω)沿式(6)与(7)对时间求导，可得:

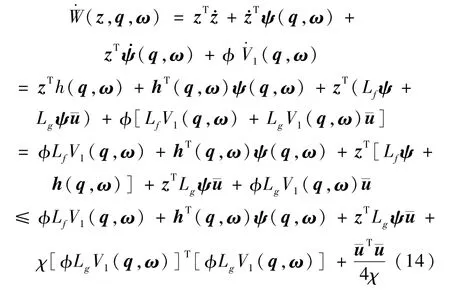
其中χ＞0，且应用了式(13)及Young不等式:

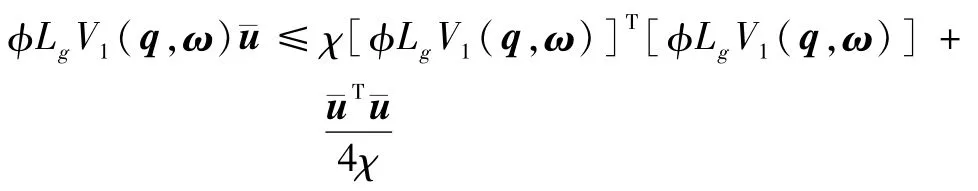
将各项求出的表达式代入式(14)可得:

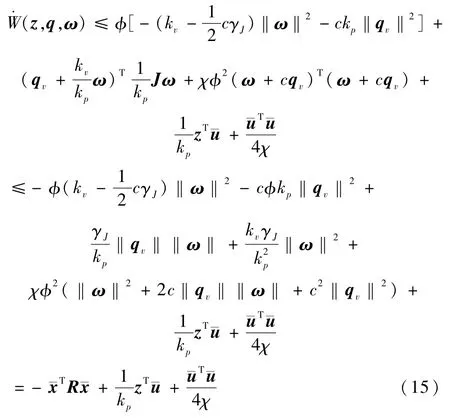
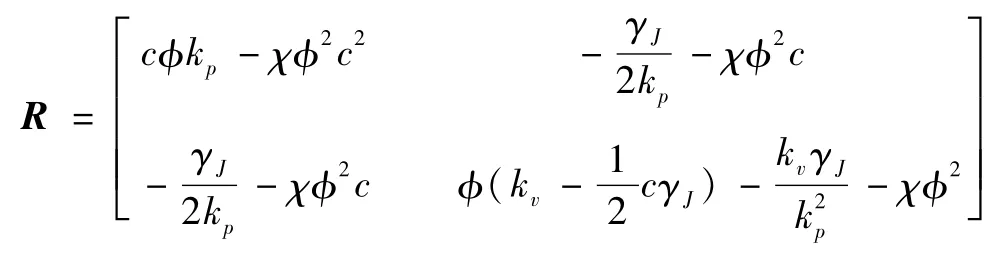
可见，若能选取参数使得矩阵 R正定(可以通过充分大的φ和充分小的 χ来实现)，那么剩下的任务就归结为证明如下不等式是成立的:

为证明式(16)，设χ=kpki/4，并注意到:

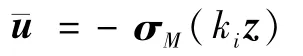
则式(16)化为:

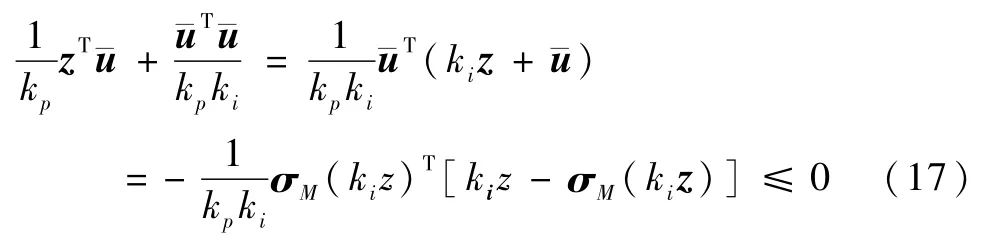
其中应用了这样的一个简单不等式:

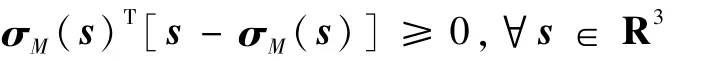
将χ=kpki/4代入矩阵R的表达式可得:

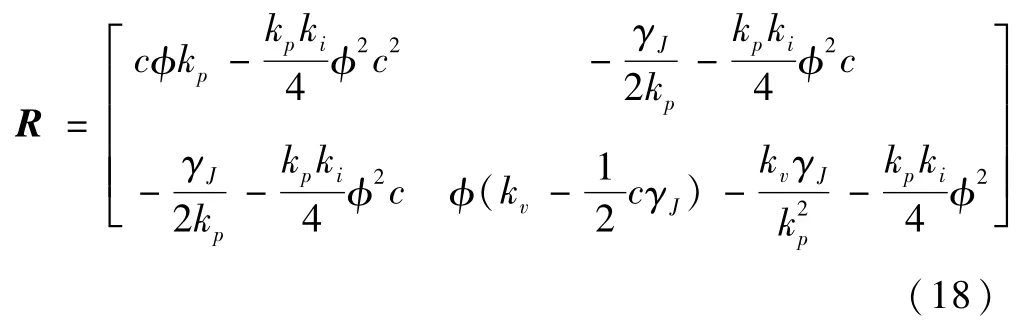
从而如果能够选择参数φ，c，kp，kυ，ki使得R＞0，那么由式(15)及式(17)可得:

由式(19)和LaSalle不变原理容易证明:

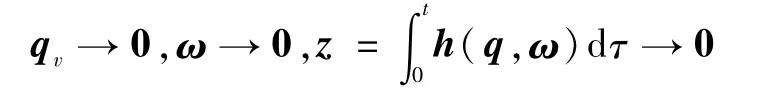
基于前面的稳定性分析，可得如下主要结论:

定理1.对于由式(1)、(2)组成的姿态系统，若设计控制律如式(3)所示，且选择参数kp，kυ，ki，使得存在参数c，φ而使

则当干扰d=0时，对于任何初始条件均有:

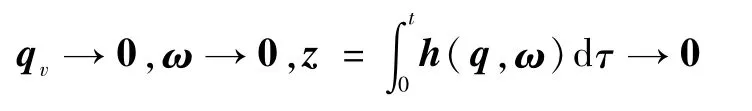
证明由前面分析直接可得，在此略.

注2.参数存在性分析:定理1要求P＞0，R＞0.不难验证，为满足P＞0，通过展开式(20)可知，只需选择充分大的φ与充分小的c即可;为满足R＞0，通过展开式(21)可知，通过选择充分大的φ与充分小的积分系数ki总可使得R＞0.一般来说，积分系数ki太小会使积分过程太慢，太大则又容易使积分超调.事实上，由式(20)、(21)可以确定一个关于积分系数ki的上限值ki，max，凡是小于ki，max的ki均能使得闭环系统渐近稳定;φ与c则是约束参数.由此可见，从式(20)、(21)确定最大容许积分系数 ki，max的过程实际上是一个具有参数约束的最优化问题(具体可用Matlab的最优化工具进行求解).

注3.某些情况下，由式(20)、(21)决定的最大积分系数ki，max可能会偏于保守，实际的仿真和工程应用中可以选择比由定理1决定的ki，max更大的积分系数.

注4.定理1给出的结论是qυ→0，从而由四元数的归一性质，有可能q0→1或q0→-1.注意到(q0，qυ，ω)=(-1，0，0)是非稳定的平衡点[1]，因此可以认为对于几乎所有的初始状态，均有 q0→1，qυ→0，ω→0，即可以认为平衡点(q0，qυ，ω)=(1，0，0)是几乎全局渐近稳定的.

注5.定理1只证明了当干扰d等于0的情形.事实上当干扰d≠0时，采用完全类似的方法也同样能够证明积分项能够在有限时间内从饱和区域进入非饱和区域，并且在积分非饱和区域内有qυ→0，ω→0，

注6.当考虑控制量的饱和时，可以设计如下形式的控制律:

可以证明在适当的参数选取之下，如上形式的饱和控制律也能够使得原系统渐近稳定.但是，由于该控制律需要消除掉陀螺力矩项，因此一般容易造成相关参数的选择过于保守，在此不再详尽分析.

3 数值实例

为说明问题，选取虚拟的刚体卫星的惯量阵为

常值干扰设置为d=[0.5，0.3，-0.4]N·m，控制器的相关参数选择为kp=5，kυ=10，M=1.由定理1求得的最大积分系数ki，max=0.6666(此时φ=5.1000，c=0.0588)，实际仿真选择为ki=0.66.初始值取为

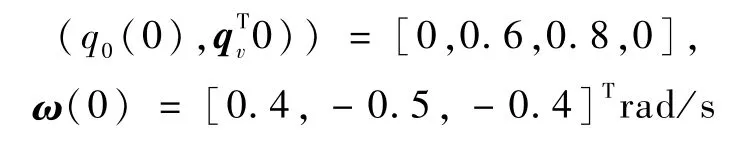
仿真结果如图1～4所示.由图1与图2可见，姿态四元数最终收敛于稳定平衡点 q=(1，0，0，0)T，角速度最终收敛于原点，可见姿态系统是渐近稳定的，并且收敛时间在比较短的40s以内.由图3可见，由于初始的姿态误差与角速度较大，控制力矩在开始时也比较大，但是很快就减小到干扰幅值附近，并最终收敛到抵消常值干扰的大小.图 4显示了积分随时间的变化曲线，在初始时，由于初始姿态误差较大，第一轴与第三轴的积分迅速上升并超过了饱和上限，然后逐渐减少到非饱和区域，直到完全和干扰相抵消.

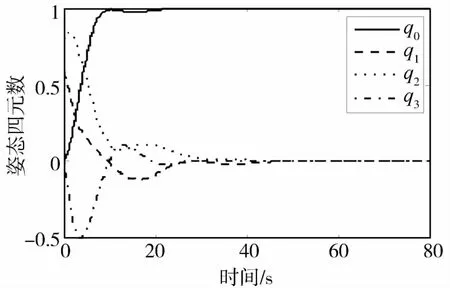
图1 姿态四元数随时间的变化曲线Fig.1 Attitude quaternion v.s.time

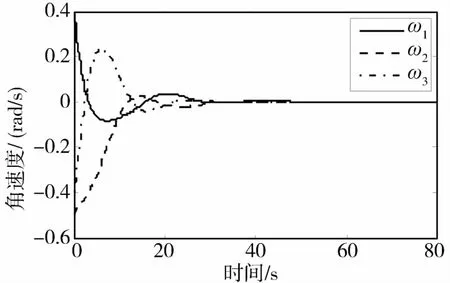
图2 角速度随时间的变化曲线Fig.2 Angular velocity v.s.time

图3 控制力矩随时间的变化曲线Fig.3 Control torque v.s.time

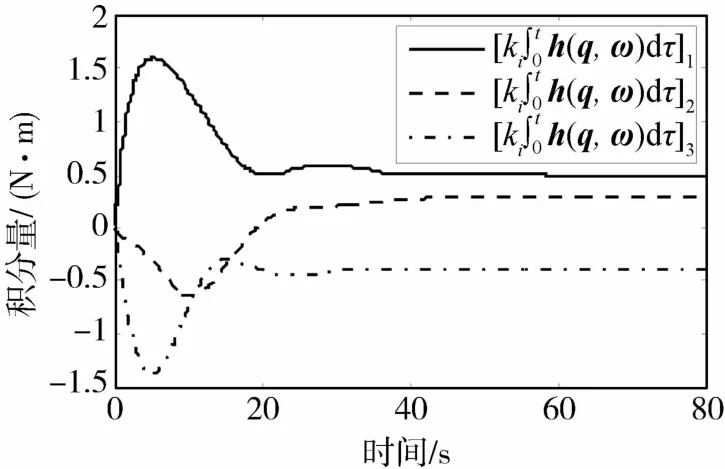
图4 积分量随时间的变化曲线Fig.4 Integrals v.s.time

以上仿真结果验证了当积分带有饱和限制时闭环系统的渐近稳定性.

4 结 论

针对存在常值干扰下的刚体卫星的非线性姿态方程，本文提出了一种具有积分饱和限制的类PID控制器，其中的积分部分是四元数与角速度的一种加权组合.然后利用前向系统的相关理论，证明了闭环系统的几乎全局渐近稳定性质，并且得出了渐近稳定的充分条件.该条件表明，只要积分系数足够小，总能够保证闭环系统是渐近稳定的.最后通过仿真验证了所提出的控制器的正确性.本文控制律的缺点是为抵消掉陀螺力矩项，需要精确知道惯量阵的信息，这是以后需要进一步解决的问题.

[1] Wen J T，Kreutz-Delgado K.The attitude control problem[J].IEEE Transactions on Automatic Control，1991，36(10):1148-1162

[2] Subbarao K.Nonlinear PID-like controllers for rigidbody attitude stabilization[J].The Journal of the Astronautical Sciences，2004，52(1&2):61-74

[3] 战毅，张洪华.全局稳定的含积分项的姿态跟踪控制律[J].控制工程，2006(1):9-16 Zhan Y，Zhang H H.A globally stabilizing attitude tracking law with integrals[J].Control Engineering，2006(1):9-16

[4] Su J，Cai K-Y.Globally stabilizing proportional-integral-derivative control laws for rigid-body attitude tracking[J].Journal of Guidance，Control，and Dynamics，2011，34(4):1260-1264

[5] Subbarao K，Akella M R.Differentiator-free nonlinearproportional-integal controllers for rigid-body attitude stabilization[J].Journal of Guidance，Control，and Dynam ics，2004，27(6):1092-1096

[6] Show L L，Juang JC，Lin C T，et al.Spacecraft robust attitude tracking design:PID control approach[C].The American Control Conference，Anchorage，AK，May 8-10，2002

[7] Bang H，Tahk M J，Choi H D.Large angle attitude control of spacecraftwith actuator saturation[J].Control Engineering Practice，2003，11:989-997

[8] Kaliora G，Astolfi A.On the stabilization of feedforward systems with bounded control[J].Systems&Control Letters，2005，54:263-270

A New Attitude Control Law w ith Saturated Integrals for Spacecraft

HU Jinchang1，2，ZHANG Honghua1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

A new PID-like attitude control law with saturated integrals is proposed for the control of spacecraft.The control law can not only elim inate the influence of constant disturbances，but prevent the control torque from getting too large by means of saturation constraint on the integrals.W ith the associated theory of forwarding system，it is rigorously proven that the closed loop is globally asymptotically stable，and the corresponding sufficient conditions of the relevant parameters are also derived.Numerical simulations demonstrate the effectiveness of the proposed approach.

attitude control;PID-like control;saturation control;forwarding system

TP273

A

1674-1579(2012)06-0018-05

10.3969/j.issn.1674-1579.2012.06.004

胡锦昌(1984—)，男，博士研究生，研究方向为卫星姿态控制;张洪华(1962—)，男，研究员，研究方向为卫星姿态控制.

2012-09-17