粉末高速压制成形密度分布的数值模拟及影响因素分析

郑洲顺，徐 丹，2，雷湘媛，应仁仁，周 文，张梦轩

（1中南大学数学科学与计算技术学院，长沙410083；2中南大学商学院，长沙410083）

粉末高速压制成形密度分布的数值模拟及影响因素分析

郑洲顺1，徐 丹1，2，雷湘媛1，应仁仁1，周 文1，张梦轩1

（1中南大学数学科学与计算技术学院，长沙410083；2中南大学商学院，长沙410083）

将研究不连续体力学行为的离散单元法应用于粉末高速压制致密化过程的研究，将粉末视为黏弹性的离散颗粒，建立粉末高速压制过程颗粒接触模型及每个颗粒的基本运动方程，推导了力与位移表达的粉末高速压制黏弹性本构关系。基于PFC软件实现了铁粉高速压制过程中粉末颗粒二维流动情况及压坯密度分布的数值模拟，模拟结果的密度分布规律与实际压制的密度分布规律较为一致；利用数值模拟结果对影响压坯密度分布的摩擦因数、高径比、双向压制因素进行了具体分析。

高速压制；离散单元法；PFC；压坯密度分布

粉末高速压制技术是一项低成本、高效率制备高密度粉末冶金零件的新技术［1－3］，因其具有良好的性价比而备受关注。在压制致密化过程中，粉末与粉末、粉末与模壁和模冲之间由于存在着摩擦，使压制过程中力的传递和分布发生改变。由于压力分布不均匀，压坯各个部分的密度和强度分布不均匀，在压制过程中产生一系列的复杂现象。目前国内外对粉末高速压制过程的研究多是将粉末视为连续体［3－5］，与粉末实际的非连续特性不符。离散单元法（Distinct Element Method，DEM）是研究不连续体力学行为的一种数值方法，该方法在粉末的堆积、流动和压制等过程的模拟中获得了成功应用［6－9］。本工作将离散单元法应用于粉末高速压制致密化过程的研究，把粉体视为颗粒的集合体，以分析粉末高速压制过程中微观颗粒的运动特性、单个颗粒行为与粉末集合体宏观行为的联系以及致密化机理。

1 模型建立

粉末高速压制成形工艺过程如图1所示，上模冲与粉末接触，液压驱动的锤头高速撞击压模产生应力波，在0．2s左右的时间内对粉体进行高能锤击，使其致密化。当高能量的冲击力载入时，粉末颗粒之间形成一定强度的结合，外力施加的能量绝大部分转变为瞬时热能和应变能。颗粒发生塑性变形甚至局部焊合，最终达到高度致密化［10］。

图1 HVC基本原理示意简图Fig．1 Basic principle of HVC

1．1 基本假设

（1）基于二维离散单元法，假设粉末颗粒为大小不一的圆盘，颗粒单元只存在空间位置的平移或转动；

（2）采用动态松弛法对颗粒运动方程进行求解，假设任一时步内速度和加速度不变；

（3）颗粒与颗粒之间的接触及颗粒与模壁之间的接触为点接触，一旦分离，相互间的法向和切向作用力为零；

（4）假设时间步长足够小，每一时间步长内扰动的传播都不超过其相邻单元［11］；

（5）接触力与重叠量有关，由力－位移定律确定，重叠量远小于颗粒尺寸。

1．2 修正的Hertz－Mindlin软接触模型

Hertz－Mindlin模型是基于Mindlin和Deresiewicz（1953）理论建立的近似非线性接触模型，采用了与法向力有关的初始剪切模量，用于模拟理想的弹性接触［8］。简化Hertz－Mindlin模型只适用于模拟无黏结、小应变、压缩应力的情况［12－15］。本模型综合考虑摩擦和黏性阻尼等因素，将颗粒与颗粒接触时的颗粒变形细节和接触力予以简化，颗粒间的法向作用处理成弹簧和阻尼器，切向作用处理成弹簧、阻尼器和滑动器。弹簧使得形变得以恢复，而阻尼器和滑动器则消耗颗粒的动能，进而表征颗粒碰撞时的形变。

如图2所示为两球形颗粒接触示意图，两球的半径分别为Ri，Rj，质量分别为mi，mj，颗粒线速度分别为u·i，u·j，转动速度分别为ωi，ωj，法向重叠量为un，法向刚度系数为Kn，dn为法相阻尼系数，对应的颗粒j作用在颗粒i上的法向力Fcn可基于Hertz理论计算：其中

－颗粒与颗粒接触时，R＝质量的折合量M对于颗粒与模壁接触时不存在阻尼项，则R－

。其中，G表示弹性剪切模量，κ表示泊松比。

图2 两球形颗粒接触示意图Fig．2 Contact relation of spherical powder particles

在切向方向增加滑动器，如果切向弹力Ks｜us｜大于最大静摩擦力μ｜Fcn｜，以静摩擦力取代弹力，方向维持原弹力方向，则切向方向的力为：

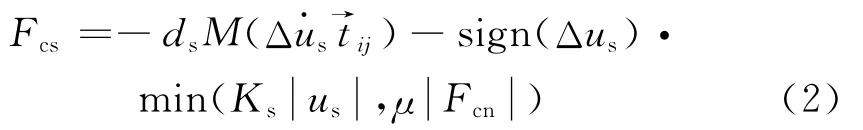
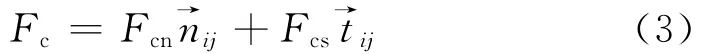
由此得到接触本构关系：

其中Mc为单元所受力矩，r＝（rn，rs）T为半径矢量。在一个时步内颗粒间叠加量和接触力予以更新

其中，ΔFc＝KΔu，Foldc，uoldc是该时步开始时的法向力和叠加量，Fnewc，unew则是该时步结束时的接触力和叠加量。

1．3 运动方程

由于作用在单元上的接触合力∑sFc可以分为弹力部分和阻尼部分，由式（4）可知阻尼部分与单元的线速度u·（t）成正比；同理，作用在单元上的接触合力矩∑sMc可分为弹力力矩部分和阻尼部分，阻尼力矩可分为弹力力矩部分和阻尼部分，阻尼部分与单元的角速度θ·（t）成正比。根据牛顿第二定律整理得高速压制过程粉末颗粒单元i的离散运动方程为：

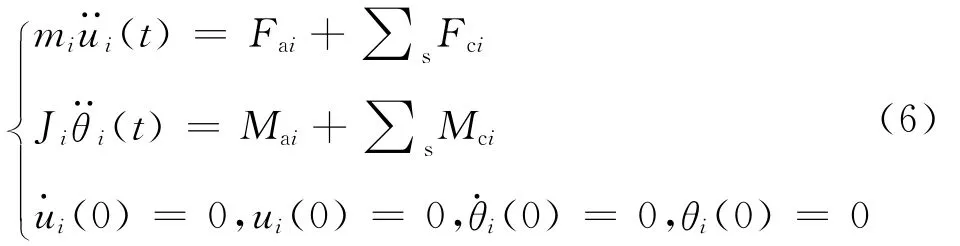
其中，J为单元转动惯量；m为单元质量；u，θ分别表示单元的位移和相对于水平位置的转动角度；u··（t），θ··（t）分别表示t时刻单元加速度和转角加速度；Fa，Ma分别为作用在单元上的主动力和主力矩，主动力包括单元所受重力，边界单元还包括初始载荷；∑sFc，∑sMc分别为作用在单元上的接触合力和接触合力矩。

表1 模拟的主要参数Table 1 The key parameters in numerical simulation

2 粉末高速压制成形致密化过程数值模拟

基于上述方程，运用离散单元法的计算软件PFC2D对铁粉的高速压制成形粉末颗粒二维流动过程进行数值模拟，用PFC软件的内置命令自动生成14000个半径均匀分布在0．384mm与0．768mm之间的圆形单元，松散地堆积在高为20cm，宽为10cm的模具内，颗粒生成后再运用半径扩大法使系统达到初始密度。根据刚性凸模压制金属粉末的实验数据［16］给出模拟所需的主要参数见表1。运用表1中的参数进行单向压制数值模拟，模拟的结果如图3，图3（a）表示压制过程中14000个粉末颗粒的初始状态，从压制开始到达到平衡用时约4ms，图3（b）表示达到平衡时的最终状态。

图3 压制过程数值模拟图（a）14000个粉末颗粒压制的初始状态；（b）压制平衡时的最终状态Fig．3 Numerical simulation of compaction process（a）space diagram of density distribution in case of unidirectional compaction；（b）platform of density distribution in case of unidirectional compaction

统计压制平衡状态的区域的密度，并运用matlab软件绘出密度分布等高线图（图4），由密度分布图不难看出，其密度的分布具有一定的规律：1）从上到下，密度减小；2）中上部分密度最大，上端两角次之，其他部分再次，下端两角密度最小；3）左右密度基本对称分布。根据黄培云教授的《粉末冶金原理》可知，成形坯的密度分布如图5所示［17］。由此可以看出，模拟的压制平衡时区域密度分布规律与成形坯密度分布基本相符合，说明该模拟结果具有可靠性。

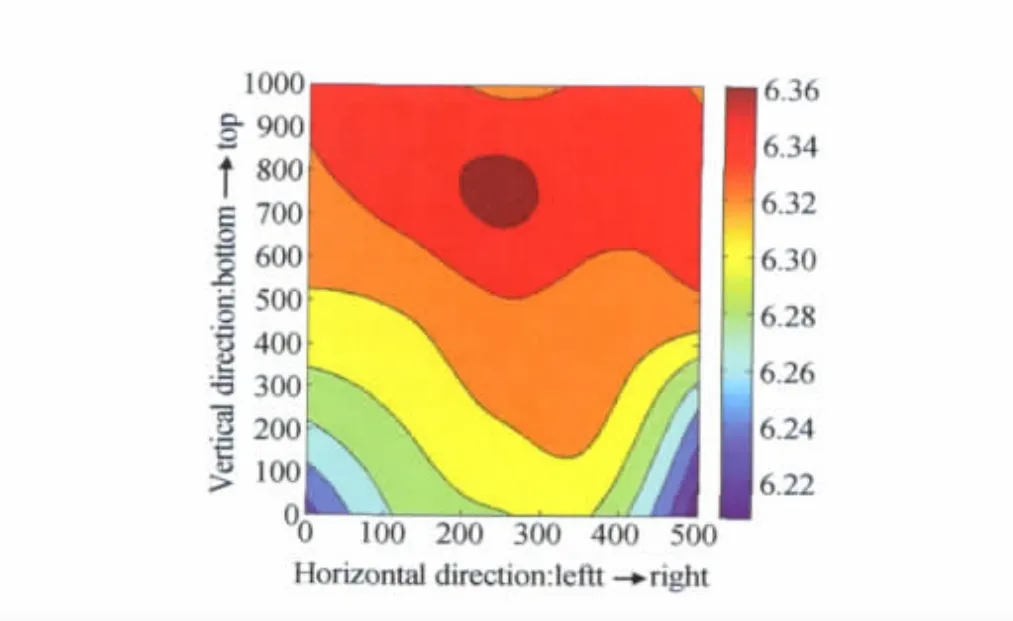
图4 单向压制区域密度分布模拟图Fig．4 Simulation diagram of density distribution in case of unidirectional compaction

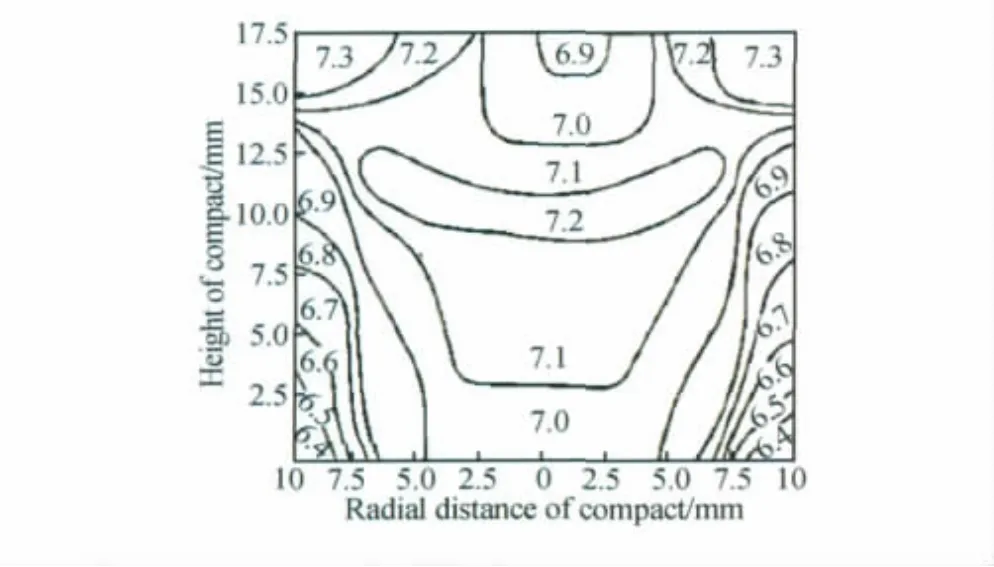
图5 成形坯密度分布［17］Fig．5 The density distribution of compact in engineering application

2．1 摩擦因数对密度分布的影响

为研究摩擦因数对密度分布的影响，在数值模拟过程中，通过改变颗粒间的摩擦因数及颗粒与模壁的摩擦因数分别控制压制过程中的内摩擦和外摩擦。表2为不同的摩擦压制条件下，模拟成形坯的平均密度及标准差，Case1为典型的单向压制；Case2为内外摩擦均可忽略不计的单向压制；Case3为仅内摩擦可忽略不计的单向压制；Case4为仅外摩擦可忽略不计的单向压制。

表2 模拟成形坯的平均密度及标准差（g／cm3）Table 2 The average density and standard deviation of the simulated compaction（g／cm3）

图6为不同的摩擦压制条件下，模拟成形坯的密度分布比较图。

图6 不同摩擦压制方式下模拟成形坯的密度分布图Fig．6 Simulation diagram of density distribution in different cases of friction coefficients

Case2：考虑摩擦因数对压制的影响，将参数表1中颗粒间的摩擦因数和颗粒与模壁的摩擦因数改为0．001（几乎没有摩擦），其他参数不变，进行数值模拟实验。实验过程中，达到平衡状态的时间延长，从4ms左右到10ms左右，产生这种结果是因为摩擦减少能量的耗散减慢，因而颗粒达到平衡所需要的时间延长；从压制的模拟结果图6（Case2）来看，与典型的压制密度分布（Case1）存在明显差异：密度明显提高；密度分布较均匀，压坯上下密度梯度基本消失。Case3：若只减小颗粒与颗粒的摩擦，当颗粒间的摩擦因数为0．001时，结合表2和图6来看，压制后的压坯密度明显高于典型单向压制（Case1），而与除去内外摩擦（Case2）基本相当，但其密度分布波动略大。Case4：从另一方面，若只减小颗粒与模壁的摩擦，当颗粒与模壁的摩擦因数为0．001时，从得到的模拟结果来看，压坯密度较典型的压制（Case1）并没有显著的提高，但压坯密度从上到下的递减趋势消失，密度呈现四周偏低而中间偏高的略微趋势。

与典型实验对比，可以说明摩擦力对压制结果的影响是显著的。首先，摩擦力直接影响到压坯最终密度，在其他参数相同的情况下，摩擦力越小，得到的压坯密度越大；其次，摩擦力影响着压坯密度的分布，摩擦力越小，密度分布越均匀。同时模拟结果表明，内摩擦为影响压坯密度的主要因素，而外摩擦为影响压坯密度分布的主要因素。由此可以看出，减小摩擦力对于压制是十分有利的，不仅可以提高压坯的密度，而且可以让得到的压坯更加均匀，性能更优良。

2．2 高径比对密度分布的影响

考虑高径比对压制的影响，将表1中的模具的高径比2∶1改为高径比1∶2进行压制模拟实验，模拟结果见图7，可以看出：其分布规律大致与典型实验相同，但差异也存在，主要表现在密度的分布上，压坯密度的标准差为0．0305g／cm3，说明当高径比变小的时候，压坯密度差别变小了。由此可知，适当减小高径比，同样可以使得到的压坯更加均匀。

图7 高径比为1∶2时的密度分布图Fig．7 Density distribution with height－diameter ratio of 1∶2

2．3 双向压制对密度分布的影响

考虑双向压制的影响，添加下模冲，给下模冲与上模冲等大反向的摩擦力，压制达到平衡时的平均密度为6．3154g／cm3，标准差为0．0336g／cm3，而典型的单向压制达到平衡时的平均密度为6．3167g／cm3，标准差为0．0387g／cm3。结合模拟结果（图8）可以看出，压制后压坯平均密度与单向压制相似，但密度的分布规律与普通单向压力存在较大的差异，由上下向中间递增，且密度分布的波动明显小于单向压制，与减小摩擦的影响类似。同样可以看到，采用双向压制也是提高压坯性能的可行方法之一，且从实际分析来看，实现双向压制比减小摩擦与改变压坯高径比相对容易实现。

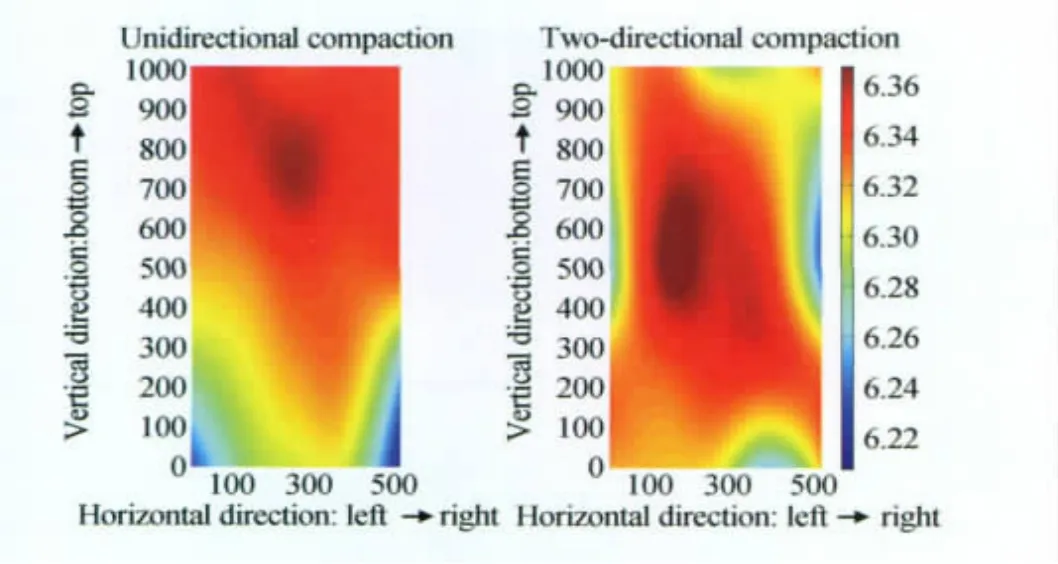
图8 单向压制与双向压制密度分布图Fig．8 Density distribution in cases of unidirectional compaction and two－directional compaction

3 结论

（1）密度的分布具有从上到下密度减小，中上部分密度最大、上端两角次之、其他部分再次、下端两角密度最小，左右密度基本对称分布的规律。

（2）减小摩擦力对于压制是十分有利的，不仅可以提高压坯的密度，而且可以让得到的压坯更加均匀，性能更优良。

（3）当高径比变小的时候，压坯密度差别变小了，适当减小高径比，对压制也很有利，同样可以使得到的压坯更加均匀。

（4）采用双向压制也是提高压坯性能的可行方法之一，且从实际分析来看，实现双向压制比减小摩擦与改变压坯高径比相对容易实现。

［1］ ORBA R L．New research directions in powder metallurgy［J］．Romanian Reports in Physics，2004，56（3）：505－516．

［2］ SKOGLUND P，HOGANAS A B，SWEDEN．High density PM components by high velocity compaction［J］．Advances in Powder Metallurgy and Particulate Materials，2002，（4）：85－95．

［3］ 周晟宇，尹海清，曲选辉．粉末冶金高速压制技术的研究进展［J］．材料导报，2007，21（7）：79－81．

［4］ 沈元勋，肖志瑜，温利平，等．粉末冶金高速压制技术的原理、特点及其研究进展［J］．粉末冶金工业，2006，16（3）：19－21．

［5］ 郑洲顺，王爽，郑珊，等．基于离散单元法的粉末高速压制流动过程模拟［J］．稀有金属材料与工程，2010，39（12）：2132－2136．

［6］ LIAN J，SHIMA S．Powder assembly simulation by particle dynamics method［J］．International Journal for Numerical Methods in Engineering．1994，37：763－775．

［7］ MATUTTIS H G，LUDING S，HERRMANN H J．Discrete element simulations of dense packings and heaps made of spherical and non－spherical particles［J］．Powder Technology，2000，109（1）：278－292．

［8］ MARTIN C L，BOUVARD D．Study of the cold compaction of composite powders by the discrete element method［J］．Acta Materialia，2003，51：373－386．

［9］ MARTIN C L，BOUVARD D，SHIMA S．Study of particle rearrangement during powder compaction by the Discrete Element Method［J］．Journal of the Mechanics and Physics of Solids，2003，51：667－693．

［10］ 果世驹，迟悦，孟飞，等．粉末冶金高速压制成形的压制方程［J］．粉末冶金材料科学与工程，2006，11（1）：24－27．

［11］ 程远方．粉体致密化过程的离散元模拟［D］．北京：北京科技大学，2000．22－25．

［12］ MINDLIN R D，DERESIEWICZ H，Elastic spheres in contact under varying oblique force［J］．J Appl Mech，1953，20：327－344．

［13］ LI Y J，XU Y，THOMTON C．A comparison of discrete element simulations and experiments for‘sandpiles’composed of spherical particles［J］．Powder Technology，2005，160：219－228．

［14］ 孙其诚，王光谦．颗粒流动力学及其离散模型评述［J］．力学进展，2008，38（1）：87－100．

［15］ 孙其诚，王光谦．颗粒物质力学导论［M］．北京：科学出版社，2009．15－17．

［16］ 温彤，COCKS A C．粉末材料压制过程的DEM分析［J］．重庆大学学报：自然科学版，2007，30（7）：1－4．

［17］ 黄培云．粉末冶金原理［M］．2版．北京：冶金工业出社，2008．204－206．

Numerical Simulation and Influential Factors Analysis of Density Distribution in High Velocity Compaction

ZHENG Zhou－shun1，XU Dan1，2，LEI Xiang－yuan1，YING Ren－ren1，ZHOU Wen1，ZHANG Meng－xuan1
（1 School of Mathematical Science and Computing Technology，Central South University，Changsha 410083，China；2 School of Business，Central South University，Changsha 410083，China）

Discrete element method which is used for studying mechanical behaviors of discontinuance is applied to studying the process of powder densification in high velocity compaction．Considering the powder as viscoelastic discrete particles，the contact model of particle flow and the equation of motion of each particle are established，constitutive model of viscoelastic powder in high velocity compaction described by force－displacement is deduced in detail．Based on computing software PFC for discrete element method，the process of the two－dimensional particle flow and density distribution during high velocity compaction are simulated．The density distribution of numerical simulation results coincide well with experiments in engineering application．The factors which affect the density distribution including friction coefficient，height－diameter ratio and two－directional compaction are analyzed．

high velocity compaction；distinct element method；PFC；density distribution

TG39

A

1001－4381（2012）07－0010－05

国家自然科学基金（50874123，51174236）；国家重点基础研究发展规划（2011CB606306）；国家大学生创新实验项目（LA09040）；中南大学优博扶植基金（2010YBFZ074）；中南大学研究生创新教育工程（2010ssxt115，2011ssxt139）

2011－10－08；

2012－03－10

郑洲顺（1964－），男，教授，博士生导师，从事偏微分方程数值解法及其应用研究，联系地址：湖南省长沙市麓山南路中南大学南校区数学院（410083），E－mail：zszheng＠mail．csu．edu．cn