非线性对流扩散方程的双线性元解的高精度分析

石东洋，董晓靖

非线性对流扩散方程的双线性元解的高精度分析

石东洋，董晓靖

（郑州大学数学系，郑州450001）

利用积分恒等式对发展型非线性对流扩散方程的双线性有限元解进行了高精度分析．给出了L2－模意义下的二阶ε一致收敛结果．进一步，根据Bramble－Hilbert引理推导出了2个高精度的积分恒等式，并由此得到了一个新的渐近展开式．

非线性对流扩散方程；双线性元；高精度

1 单元构造及逼近问题

方程（1）对应的变分形式为：求u∈H10（Ω），使得

设Th是Ω的一族均匀剖分，即Ω＝e珋．e∈Th为x－y平面上的一个矩形单元，其边长分别为2he、2ke，h＝｛he，ke｝，4个顶点分别为a1（xe－he，ye－ke）、a2（xe＋he，ye－ke）、a3（xe＋he，ye＋ke）、a4（xe－he，ye＋ke），4条边分别为li＝aiai＋1（mod 4）（i＝1，2，3，4）．设＾e为ξ－η平面上的参考单元，＾a1（－1，－1）、2（1，－1）、＾a3（1，1）、＾a4（－1，1）为4个顶点，＾li＝＾ai＾ai＋1（mod 4）（i＝1，2，3，4）为4条边．在参考单元构造双线性元（，＾P，＾Σ）：＾Σ＝｛＾vi，i＝1，2，3，4｝，＾P＝Q1（＾e）＝span｛1，ξ，η，ξη｝，其中＾vi为＾v在顶点＾ai（i＝1，2，3，4）处的函数值．＾e上的双线性插值定义为：，其中：ξi＝（－1，1，1，－1），ηi＝（－1，－1，1，1）．定义从参考单元＾e到一般单元e的可逆仿射变换Fe：＾e→e，x＝xe＋heξ，y＝ye＋keη，那么，相应的有限元空间和插值算子分别为：

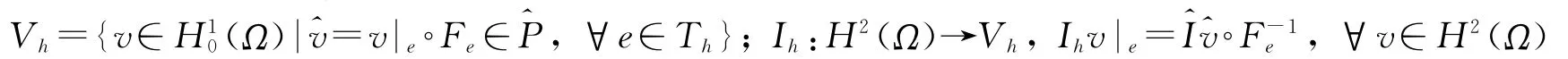
所以，变分问题（2）的协调有限元半离散格式为：求uh∈Vh，满足

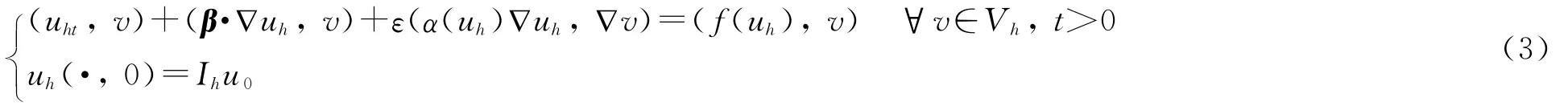
2 一致收敛性分析

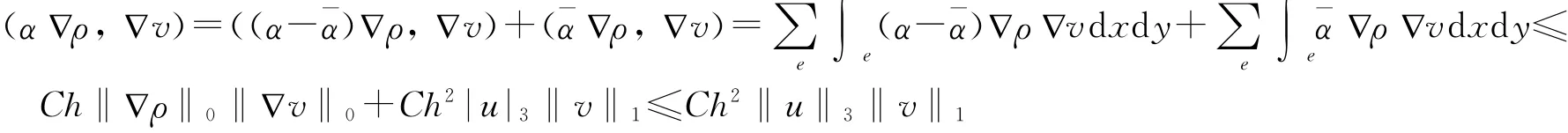
记ρ＝u－Ihu和θ＝uh－Ihu．为了估计需要以下引理．

引理1［7］∫Ωρxvdxdy≤Ch2‖u‖3‖v‖0，∫Ωρxvxdxdy＝Ch2‖u‖3‖v‖1，v∈Vh．

引理2［6］（β·!ρ，v）≤Ch2‖u‖3‖v‖0，v∈Vh．

引理3 设α∈W1，"（Ω），则（α!ρ，!v）≤Ch2‖u‖3‖v‖1，v∈Vh．

定理1 设u和uh分别是问题（2）和问题（3）的解，且u∈H3（Ω），α∈W1，"（Ω），β∈（W1，"（Ω））2，则有如下一致收敛性结果：

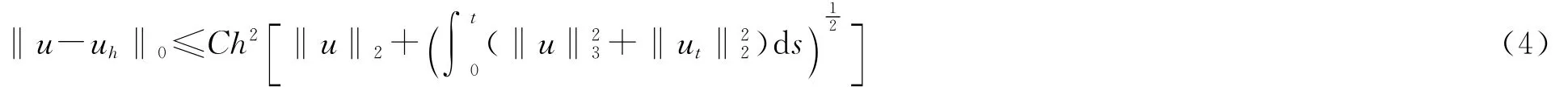
其中常数C不依赖于扩散参数ε．

证明 对任意的v∈Vh，由式（2）和式（3）得到误差方程

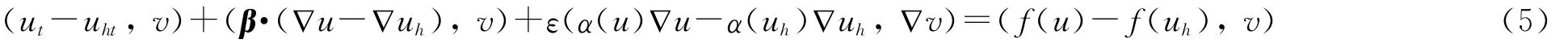
即

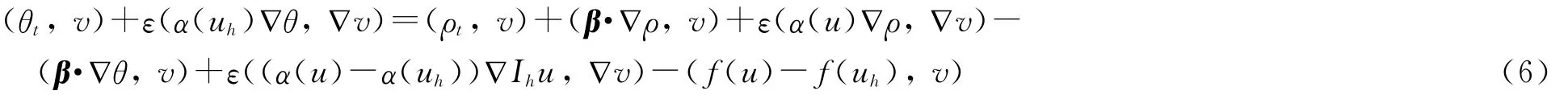
在式（6）中取v＝θ，则有

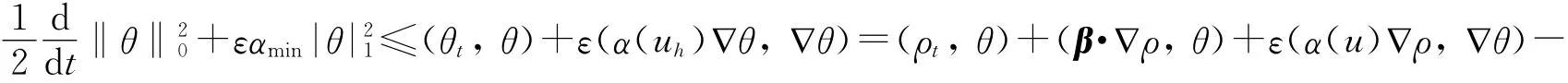
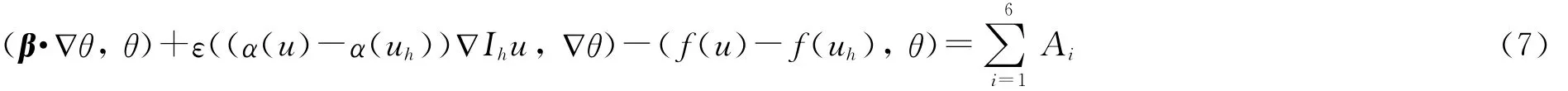
利用引理1～3可逐项估计Ai（i＝1，2，…，6）：

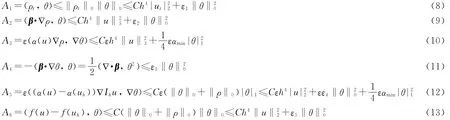
将式（8）～式（13）带入式（7），整理可得

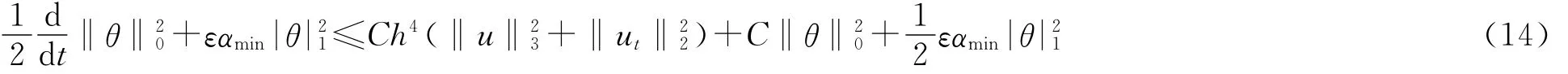
那么有

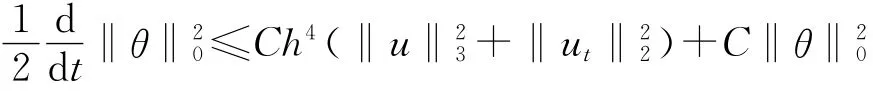
上式两端从0到t积分，注意到θ（0）＝0，利用Gronwall引理得到

3 双线性元的渐近展开式

为了得到双线性元的渐近展开式，需要高精度的积分恒等式如下：

引理4［8］设u∈H4（Ω），v∈Vh，有

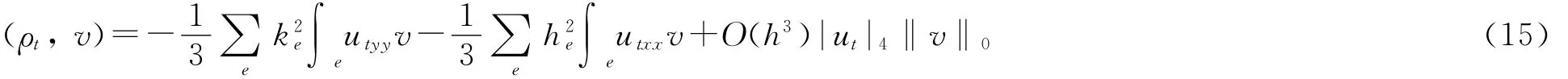
引理5 设α∈H2（Ω），β∈（H2（Ω））2，u，ut∈H4（Ω），v∈Vh，则有

证明 仅给出式（16）的证明，式（17）类似可得．定义Pi（e）为单元e上的i阶多项式空间，定义插值Π1：H2（Ω）→Vh：∫e（w－Π1w）qdxdy＝0，q∈P1（e），则Π1βi＝ai＋bi（x－xe）＋ci（y－ye），i＝1，2；Π1α＝a＋b（x－xe）＋c（y－ye），其中ai、bi、ci和a、b、c分别是βi和α的一次插值常系数．＾v∈＾P，考察函数

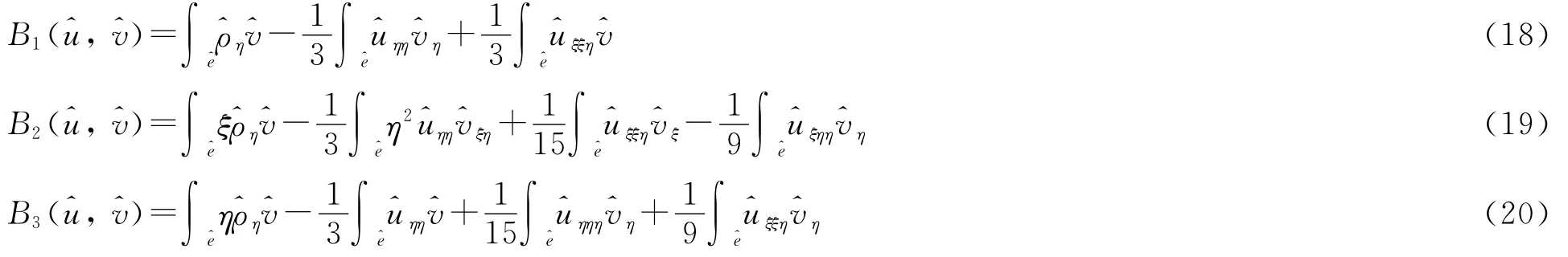
根据Sobolev嵌入定理和反不等式有

当＾u取ξ2、η2、ξ3、ξ2η、ξη2、η3时，相应的插值＾I＾u分别为1、1、ξ、η、ξ、η，直接计算可得

根据Bramble－Hilbert引理和式（21）有

通过Scaling技巧将式（18）～式（20）转化到一般单元上的积分变换

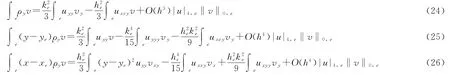
类似计算可得

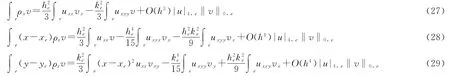
组合式（24）～式（29）并利用Green公式可得

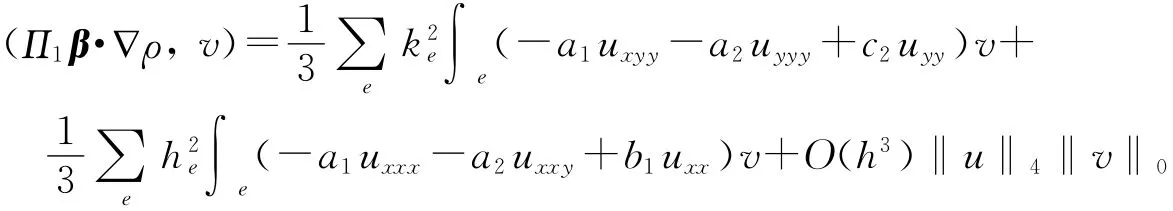
所以

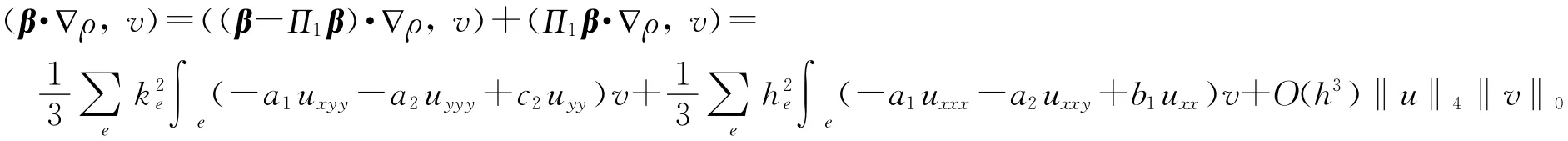
注1 以上这些高精度结果是用一般的插值方法得不到的．

定理2 设α∈H2（Ω）∩W1，"（Ω），β∈（H2（Ω）∩W1，"（Ω））2，u、ut∈H4（Ω）∩H10（Ω），则存在φh∈Vh使得

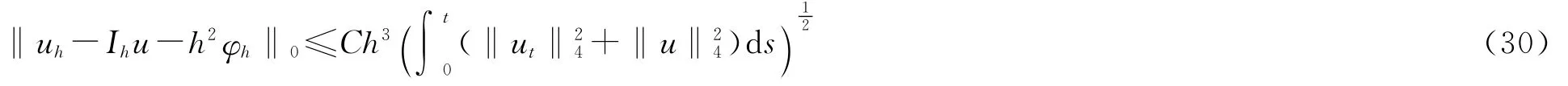
其中常数C不依赖于扩散参数ε．

证明 由引理4～5及式（6）知

其中：f1＝－utyy＋εauxxyy－εcuyyy－a1uxyy－a2uyyy＋c2uyy，f2＝－utxx＋εauxxyy－εbuxxx－a1uxxx－a2uxxy＋b1uxx．

构造辅助问题

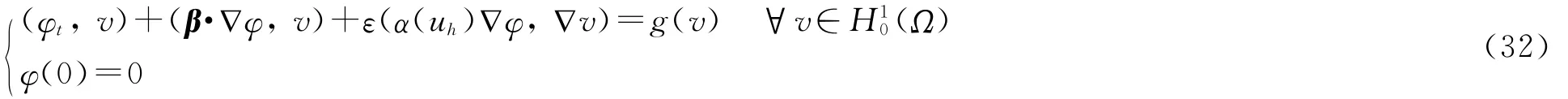
故g（v）是H10（Ω）中的有界线性泛函，从而辅助问题（32）有唯一解φ．

辅助问题（32）的协调有限元的离散格式为：求φh∈Vh，满足

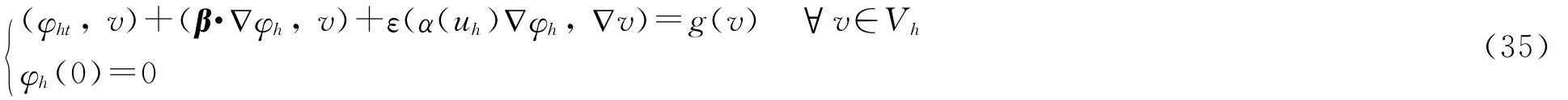
由式（31）和式（35）可得

取v＝θ－h2φh，则有

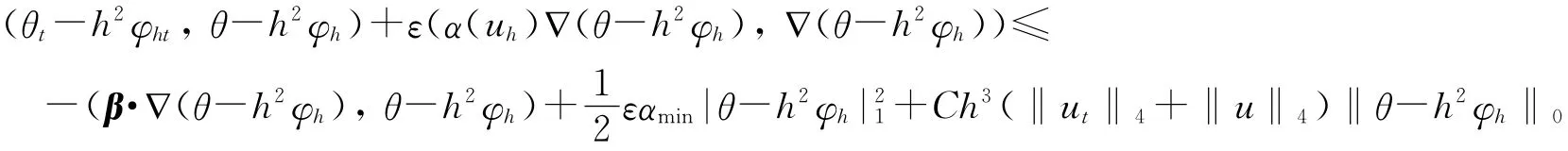
即

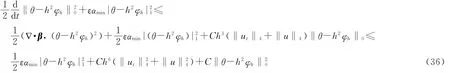
对式（36）两端积分，并注意到θ（0）－h2φh（0）＝0可得

其中常数C不依赖于扩散参数ε．最后利用Gronwall引理即可得证．

注2 到目前为止，如何导出对流占优扩散方程的协调有限元方法在H1－模意义下的ε一致收敛性仍是一个尚未解决的问题．

［1］ YANG D P．Analysis of least－squares mixed finite element methods for nonlinear non－stationary convection－diffusion problem［J］．Math Comp，2000，69：929－936．

［2］ WANG H．An optimal－order error estimate for an ELLAM scheme for two－dimensional linear advection－diffusion equation［J］．SIAM J Numer Anal，2000，37：1338－1368．

［3］ BAUSE M，KNABNER P．Uniform error analysis for Lagrange－Galerkin approximation of convection domainated problems［J］．SIAM J Numer Anal，2002，39：1954－1984．

［4］ 朱国庆，陈绍春．一个新非协调单元对扩散对流反应方程的应用［J］．数学的实践与认识，2010，40（8）：126－131．

［5］ WANG K X，WANG H．An optimal－order error estimate to the modified method of characteristics for a degenerate convection－diffusion equation［J］．Int J Numer Anal Model，2009，6：221－231．

［6］ LIN Q，WANG H，ZHANG S H．Uniform optimal－order estimates for finite element methods for advection－diffusion equations［J］．J Sys Sci Compl，2009，22：555－559．

［7］ 林群，严宁宁．高效有限元构造与分析［M］．保定：河北大学出版社，1996．

［8］ LIN Q，LIN J F．Finite Element Methods：Accuracy and Improvement［M］．Beijing：Science Press，2006．

（责任编校 马新光）

Higher accuracy analysis for bilinear finite element solution of nonlinear advection－diffusion equation

SHI Dong－yang，DONG Xiao－jing
（Department of Mathematics，Zhengzhou University，Zhengzhou 450001，China）

By using integral identities，the higher accuracy approximation of bilinear conforming finite element for the time－dependent nonlinear advection－diffusion equations is investigated．The optimalεuniform convergent result is obtained under L2－norm．Based on Bramble－Hilbert lemma，two new integral identities and a asymptotic error expansion are derived．

nonlinear advection－diffusion equation；bilinear finite element；higher accuracy

book=1,ebook=68

O241．21

A

1671－1114（2012）02－0001－05

2011－11－29

国家自然科学基金资助项目（10971203）；高等学校博士学科点专项科研基金资助项目（20094101110006）

石东洋（1961－），男，教授，主要从事有限元方法及应用方面的研究．