非线性方程求根的高阶迭代方法

倪克琳，李宝毅

非线性方程求根的高阶迭代方法

倪克琳，李宝毅

（天津师范大学数学科学学院，天津300387）

通过对已有误差方程进行加权组合，消去较低阶数，得到了3个新的带参数四阶收敛迭代公式和1个新的五阶收敛迭代公式，收敛效率分别达到了1．587和1．495，并证明了这些公式的局部高阶收敛性．最后通过数值算例验证了这些方法的有效性．

非线性方程；Newton法；迭代方法；四阶收敛；五阶收敛

在科学与工程计算中经常遇到非线性方程f（x）＝0，这类问题常常不能用解析方法求得其精确解，而只能用数值方法求得其近似解．常用的数值方法主要有简单迭代法、牛顿迭代法、弦割法、抛物线法等［1－4］，其中牛顿迭代法（CN法）是非线性方程求根的一种基本方法．

牛顿法是求解非线性方程近似根的一个有效方法，它需要用到函数值与导数值，是众所周知且应用最广泛的公式．牛顿法对于单根通常具有二阶收敛速度，如何对该方法进行修改，使之具有更高的收敛速度是当今国内外研究的热点问题之一．目前已有许多新的迭代公式被提出［1－7］，迭代收敛阶数得到了明显提高．本研究基于已有公式，对它们的误差方程进行加权组合，消去较低阶数，得到了一些新的四阶和五阶收敛迭代方法．

1 预备知识

定义1 设α∈R，xn∈R，n＝0，1，2，…．若对于某迭代法，有序列｛xn｝收敛于α，第k次迭代误差ek＝xk－α，且存在常数c≥0，非负整数p，使得，则称迭代序列｛xn｝是p阶收敛的．ek＋1＝cekp＋ O（ep＋1k）称为误差方程．

定义2 设｛xn｝是p阶收敛（p≥1）的迭代序列，每一步迭代中计算函数值和导数值的次数和为μ，则称E＝为迭代法的收敛效率．

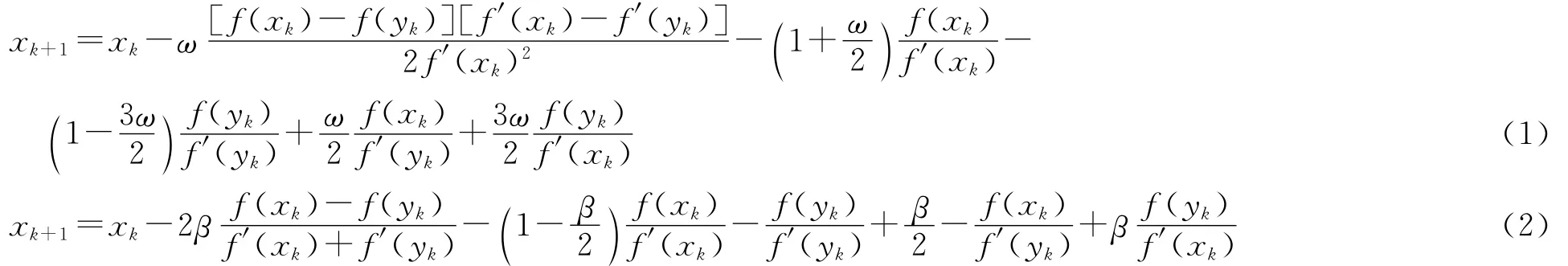
式（1）的误差方程为

式（2）的误差方程为

证明 f（xk）、f′（xk）、f（yk）、f′（yk）在α处的Taylor展开式为：

由式（3）～式（6）可得

将式（13）、式（7）～式（10）做线性组合，表出系数分别为ω、a1、a2、a3、a4，则有

令ek、e2k、e3k的系数分别为1、0、0，解方程得，则式（15）变为

由此可得式（1）及其误差方程．

将式（14）、式（7）～式（10）做线性组合，表出系数分别为β、b1、b2、b3、b4，则有

令ek、ek2、ek3的系数分别为1、0、0，解得b1＝1－，b2＝1，b3＝－，b4＝－β，则式（16）变为

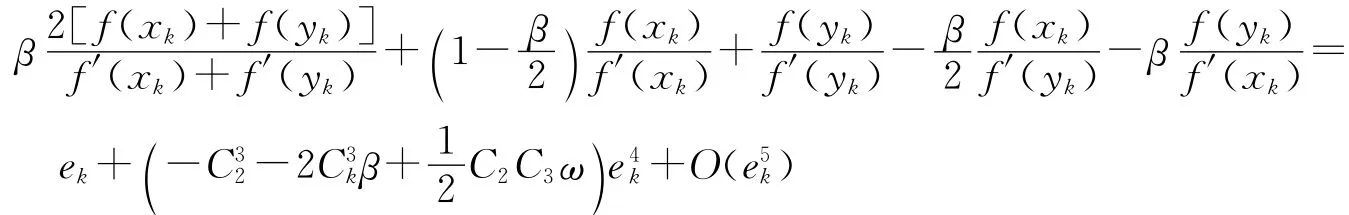
由此可得式（2）及其误差方程．证毕．

2 新的迭代方法

令ek、ek4的系数分别为1、0，解得则式（18）转化为

由此得到式（17）及其误差方程．证毕

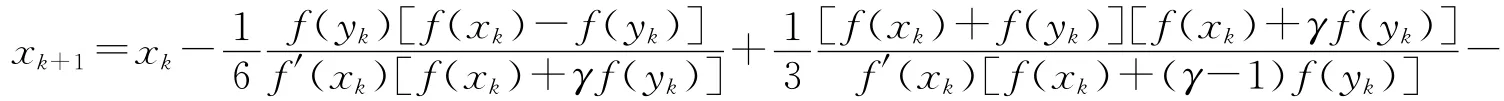
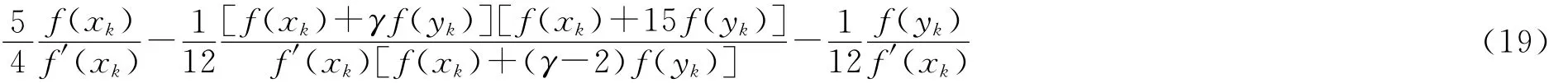
其中γ是参数，且其误差方程为ek＋1＝（2γC32－C2C3）e4k＋O（e5k）．

再由式（7）、式（10）、式（20）～式（22）即可得式（19）的误差方程．证毕．

其误差方程为ek＋1＝［C22（1＋2γ－2ω－2ωγ）－C2C3］e4k＋O（e5k）．

再由式（7）、式（10）、式（20）、式（24）即可得式（23）的误差方程．证毕．

其误差方程为ek＋1＝－［C2C3＋C32（－1＋βγ－2β－2γ）］e4k＋O（e5k）．

定理中四阶收敛的迭代公式（19）、（23）、（25）均需要计算2次函数值和1次一阶导数值，因此它们的收敛效率均等于≈1．587．而五阶收敛的迭代公式（17）需要计算2次函数值和2次一阶导数值，因此它的收敛效率等于≈1．495．

3 数值结果

以下数值结果均使用Mathematica7．0求得．在计算机程序中设定终止条件为：（ⅰ）｜xn＋1－xn｜＜ε；（ⅱ）｜f（xn）｜＜ε；（ⅲ）最大迭代次数为150．当满足中止条件时，xn＋1就看作精确根α的计算值．各种迭代算法中均取ε＝10－18．使用以下常用函数进行测试［6］：

表1和表2是将所得到的新迭代公式中的参数取不同值并与经典公式做对比，进而比较各公式的收敛速度．其中IT是当结果充分接近0时的迭代次数，NEF是迭代过程中总的计算函数的次数．表中符号表示公式如下：

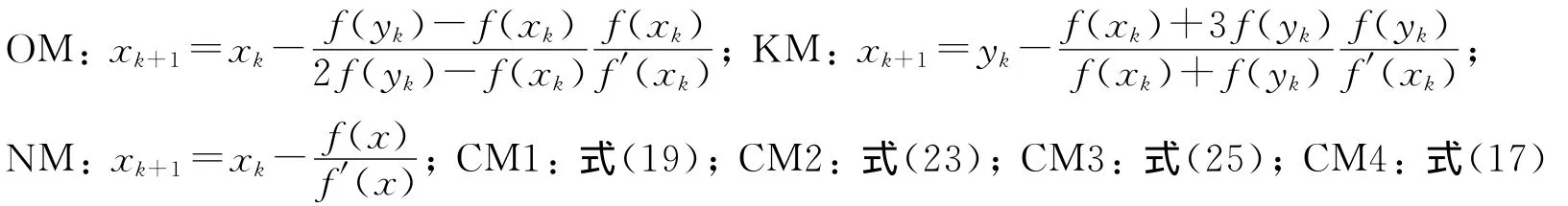
表1 各种迭代公式迭代次数、总函数计算次数比较（β＝－1，ω＝，γ＝）Tab．1 Comparison of total number of times of function calculating and iterations of every iterative method（β＝－1，ω＝，γ＝）

表1 各种迭代公式迭代次数、总函数计算次数比较（β＝－1，ω＝，γ＝）Tab．1 Comparison of total number of times of function calculating and iterations of every iterative method（β＝－1，ω＝，γ＝）

f（x）IT NEF初值NM KM OM CM1CM2CM3CM4NM KM OM CM1CM2CM3CM4 f1－0．5 100 11 15 32 11 14 14 200 33 45 96 33 42 56 f1－0．3 55 49 61 28 8 45 6 110 147 183 84 24 135 24 f2－1．5 6 4 4 4 4 4 43 12 12 12 12 12 12 172 f21．5 6 4 4 4 4 4 3 12 12 12 12 12 12 12 f3－1 5 5 3 3 3 3 3 10 15 9 9 9 9 12 f33 27 7 12 3 15 10 10 54 21 36 9 45 30 40 f4－1．5 6 5 4 4 4 4 4 12 15 12 12 12 12 16 f41．5 6 5 4 4 4 4 4 12 15 12 12 12 12 16 f53 8 5 5 5 4 4 4 16 15 15 15 12 12 16 f54 8 6 5 5 5 5 4 16 18 15 15 15 15 16 f60．2 5 4 3 3 3 4 3 10 12 9 9 9 12 12 f61 6 4 4 4 4 7 4 12 12 12 12 12 21 16 f70．5 5 4 3 3 3 3 3 10 12 9 9 9 9 12 f71 5 3 3 3 3 3 3 10 9 9 9 9 9 12 f8－1．3 5 4 3 3 3 3 3 10 12 9 9 9 9 12 f80．3 21 15 6 11 12 15 14 42 45 18 33 36 45 56

表2 各种迭代公式迭代次数、总函数计算次数比较（β＝1，ω＝1，γ＝1）Tab．2 Comparison of total number of times of function calculating and iterations of every iterative method（β＝1，ω＝1，γ＝1）

表1和表2的结果显示，本研究迭代法的收敛速度比牛顿法快很多且需要计算的函数值要少．此外根据所测试的多个函数可以看出，本研究方法收敛速度与那些著名的经典方法基本相同，且总的计算函数的数量大体相同．

［1］ RICHARD I，BURDEN J，DOUGLAS F．Numerical Analysis［M］．Beijing：Higher Education Press，2001．

［2］ FRINTINI M，SORMANI E．Some variant of Newton＇s method with third－order convergence［J］．Comput Appl Math，2004，140：419－426．

［3］ HOMEIER H H H．On Newton－type methods with cubic convergence［J］．Comput Appl Math，2005，176：425－432．

［4］ POTRA F A，PTAK V．Nondiscrete induction and iterative processes［J］．Research Notes in Mathematics，1984，29（3）：505－506．

［5］ CHUN C．A simply constructed third－order modifications of Newton＇s method［J］．Comput Appl Math，2008，219：81－89．

［6］ CHUN C．Construction of Newton－like iteration methods for solving nonlinear equations［J］．Numer Math，2006，104（3）：297－315．

［7］ OSTROWSKI A M．Solution of Equations and Systems of Equations［M］．New York：Academic Press，1966．

（责任编校 马新光）

High－order iterative method for searching root of nonlinear equation

NI Ke－lin，LI Bao－yi
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

Three new fourth order convergent iteration formulas with parameters and a new five order convergent iteration formula are obtained by using the weighted combination of existing error equations and eliminating the lower order terms，and their convergence efficiencies reach to 1．587and 1．495respectively．The local high order convergences of the formulas are determined，and the effectiveness of these methods are verified by using numerical examples．

nonlinear equation；Newton method；iterative method；fourth order convergence；five order convergence

book=2012,ebook=26

O241．7

A

1671－1114（2012）02－0032－06

2011－09－07

国家自然科学基金资助项目（11026197）

倪克琳（1987－），女，硕士研究生．

李宝毅（1963－），男，教授，主要从事常微分方程及其应用方面的研究．