Kantorovitch算子在Wiener空间下的平均误差

高兴瑞，许贵桥

Kantorovitch算子在Wiener空间下的平均误差

高兴瑞，许贵桥

（天津师范大学数学科学学院，天津300387）

在加权Lp范数下讨论Kantorovitch算子列在Wiener空间下的平均误差，得到了相应量的强渐近阶．

Kantorovitch算子；加权Lp范数；Wiener空间；平均误差

设F是一个实可分的Banach空间，μ是定义在F的Borel子集上的概率测度．设H是另一个范数为‖·‖的赋范空间，F连续嵌入在H中．任意使得f→‖f－A（）f‖为可测映射的算子A：F→H被称作一个逼近算子．算子A的p平均误差为［1］

设X是定义在［0，1］上的连续函数f的集合，在X上赋予最大范数，f（0）＝0．X上的Wiener测度μ由下列性质唯一确定：对任意n≥1，Rn上的Lebesgue可测集B及0＝t0＜t1＜…＜tn≤1，

其中u0＝0．由文献［2］可知

对于ρ∈L1［0，1］，ρ≥0，f∈C［0，1］的加权Lp范数定义为，当ρ（）t＝1时简记为‖·‖p．

对于f∈C［0，1］，f的n次Kantorovitch多项式为

f的n次Bernstein多项式为

其中：

文献［3］讨论了Bernstein多项式列在Wiener空间下的平均误差，得到了相应量的弱渐近阶，本研究考虑Kantorovitch算子列在Wiener空间下的平均误差，得到

定理 设Kn（f，x）如式（3）定义．对于任意ρ∈L1［0，1］，ρ＞0，ρ（x）在（－1，1）连续，1≤p＜"，有

由定理和Hölder不等式可得如下推论．

推论 设Kn（f，x）如式（3）定义．对于任意ρ∈L1［0，1］，ρ＞0，ρ（x）在（－1，1）连续，1≤p，q＜"，有

对于正数序列a｝｛n和b｝｛n，an≈bn表示存在与n无关的常数C，使得an／C≤bn≤Can，不同表达式中的C可能不同．

引理1［4］对于固定的渐近关系

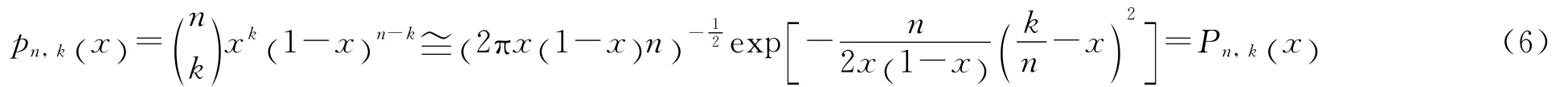
对于所有x∈［δ，1－δ］和所有满足不等式

的k一致成立，换句话说，

对于所有满足式（7）的k一致成立．

设X＝x （1－x），且设

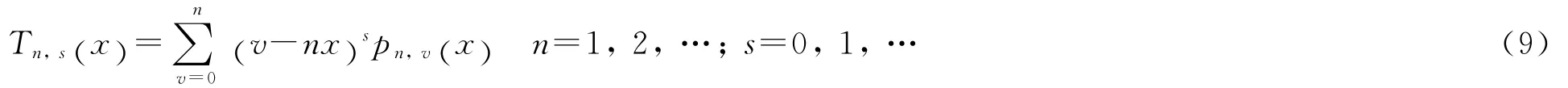
引理2［5］对于固定的s＝0，1，…，Tn，s（）x是一个关于x次数小于s的多项式，且有

这里aj，s，bj，s是系数与n无关且次数不大于s－j的多项式．特别地

定理的证明 由文献［2］可得

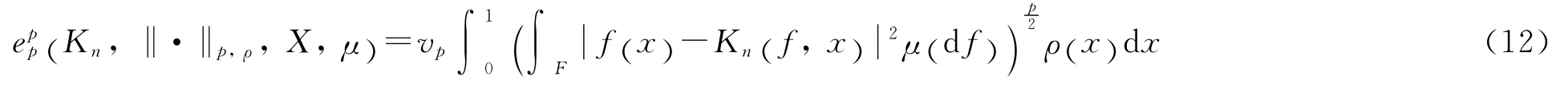
由式（3）可得

由式（1）得

由式（11）和简单的计算可得

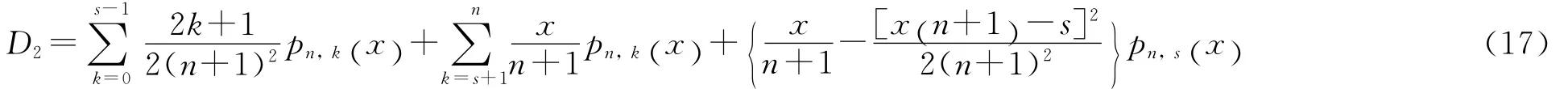
类似可得

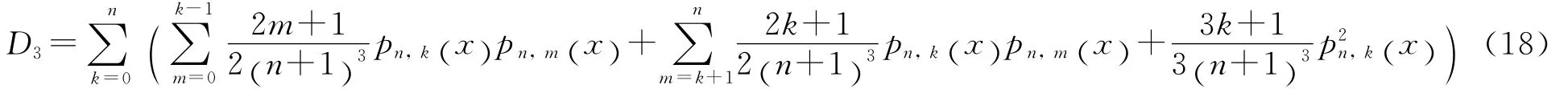
由式（13）～式（18）可得

由式（8）可知

由式（20）可得

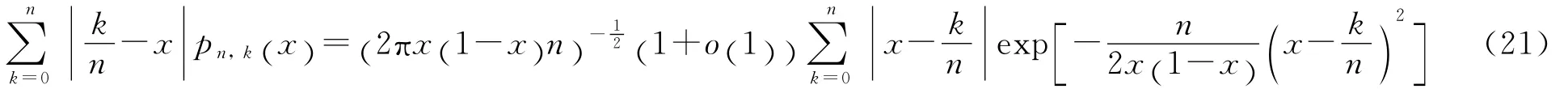
简单计算可得

直接计算可得

由式（21）～式（25）可得

类似可得

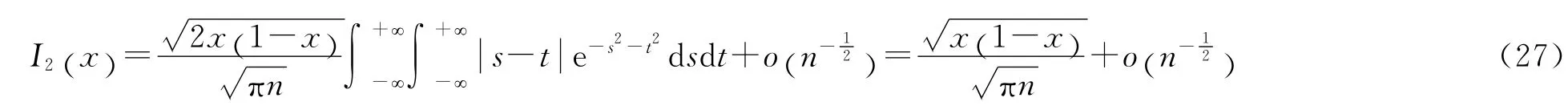
简单计算易得

由式（19）和式（26）～式（28）可得

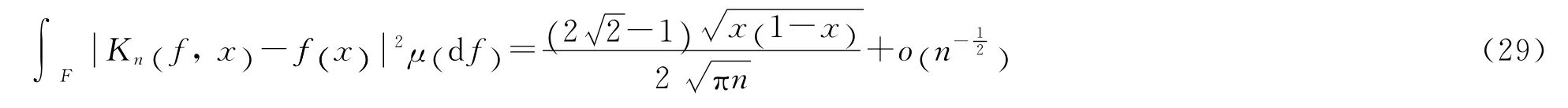
［1］ TRAUB J F，WASILKOWSKI G W，WOZNIAKOWSKI H．Information－Based Complexity［M］．New York：Academic Press，1998．

［2］ KLAUS R．Average－Case Analysis of Numerical Problems［M］．Berlin：Springer－Verlag，2000．

［3］ XU G Q，DU Y F．The average errors for Hermite－Fejer interpolation on the Wiener Space［J］．Science in China：Mathematics，2010，53（7）：1841－1852．

［4］ LORENTZ G G．Bernstein Polynomials［M］．Toronto：University of Toronto Press，1953．

［5］ DEVORE R A，LORENTZ G G．Constructive Approximation［M］．Berlin：Springer－Verlag，1993．

（责任编校 马新光）

通过类似的证明可知对于

Average errors for Kantorovitch operators on Wiener space

GAO Xing－rui，XU Gui－qiao
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

For weighted approximation in Lp－norm，the strongly asymptotically orders for the average errors of function approximation by the Kantorovitch operators sequence on the Wiener space are determined．

Kantorovitch operators；weighted Lp－norm；Wiener space；average error．

book=2012,ebook=18

O174．42

A

1671－1114（2012）02－0018－04

2011－07－05

高兴瑞（1987－），男，硕士研究生．

许贵桥（1963－），男，教授，主要从事函数逼近论方面的研究．