斜齿轮时变接触线改进算法及螺旋角对接触线影响

李文良，王黎钦，常山，赵小力

(1.哈尔滨工业大学机电工程学院，哈尔滨150001;2.中国船舶重工集团公司第七〇三研究所，哈尔滨150078)

斜齿轮在高速列车、航空发动机以及舰船等需传递重载的设备中广泛应用［1-2］.接触线的时变性是斜齿轮传动的主要特点之一［3-4］，由于接触线数目的变化会引起刚度、齿面摩擦力的改变，是振动和噪声的激励源之一［5-8］.Kubo和Kiyono研究表明随着斜齿轮螺旋角增大，斜齿轮在啮合过程中接触线数目增加，有助于减少激振力使得运行平稳，这是斜齿轮工作的一大优点［9］.但是该研究没有给出螺旋角对时变接触线的影响规律.Smith提出斜齿轮的转动导致啮合面内接触线的变化，并计算了接触线的最大值和最小值［10］.Chinmaya Kar和 A.R.Mohanty［11］采用一种简化的方法计算接触线的长度，但是这个算法受到啮合面形状限制，只适用于啮合面宽度在一个端面齿距和2个端面齿距之间，而且最多只能计算同时有3条接触线的情况，算法受到局限所以不具有普适意义.

早期的文献以及标准中大部分都只是给出了斜齿轮接触线的最大值、最小值以及均值，本文采用通用公式利用计算机编程计算，突破了Chinmaya Kar和A.R.Mohanty提出的算法受啮合面形状以及接触线条数的限制条件［11］，可以计算出任意条接触线的长度以及在一个端面齿距周期内任意时刻接触线总长度.在此基础上分析了螺旋角对接触线长度变化的影响，以便发现其变化规律，为后续齿轮时变刚度、接触线载荷分布以及修形计算等提供理论依据.

1 斜齿轮时变接触线算法

由于文献［11］在推导过程中受到条件限制，不能实现快速计算，工程上应用不方便.本文在文献［11］的基础上推导出通用公式，采用计算机编程计算，此程序不受啮合区形状以及同时啮合接触线数目的限制.

本文根据不同齿轮啮合形成的啮合面的特点，以齿轮宽度与啮合面的宽度比值(b/f)与1的关系作为计算准则，推导出通用的计算时变接触线的公式，接触线示意图如图1所示，考虑3种情况推导公式如下.

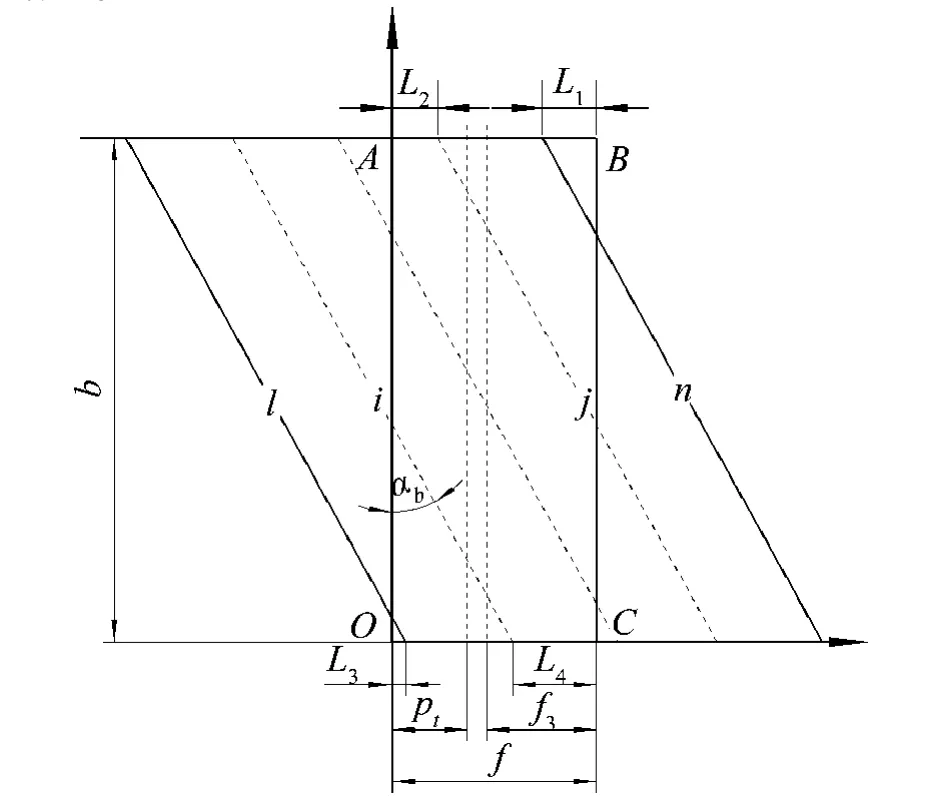
图1 斜齿轮啮合区坐标以及接触线示意Fig.1 Schematic illustration of coordinate and contact line in the pressure plane

情况1 当b/f＞1时:

接触线的条数n为

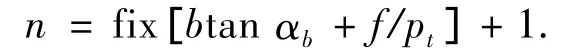
啮合面的宽度f范围内的接触线的条数m为

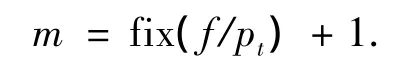
当接触线的另一端与啮合面内的对角点的关系表达式为

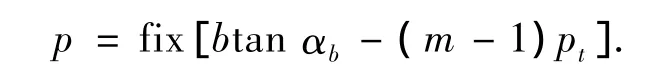
当p=0接触线一端到达对角点C，p≠0时则越过对角点C.

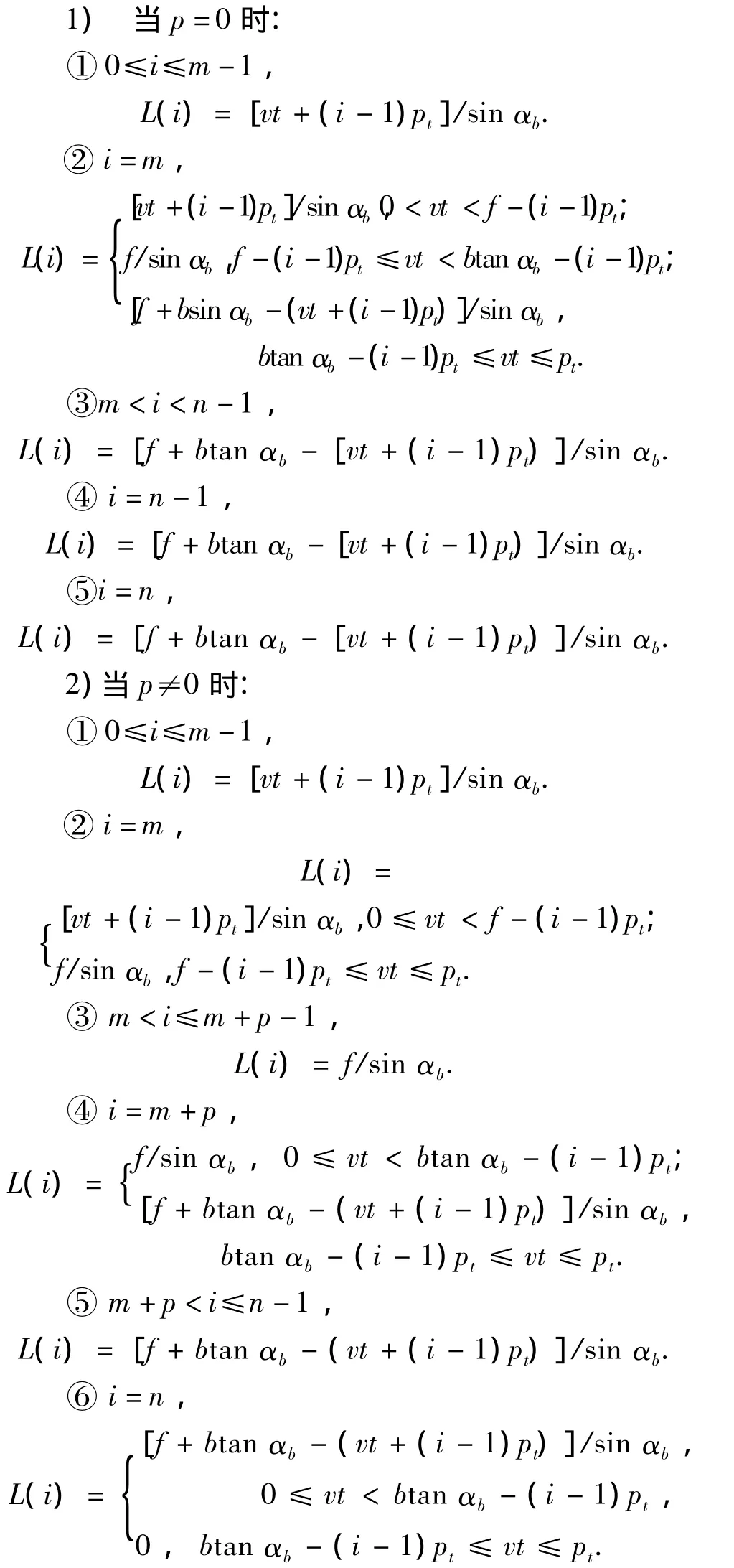
情况2 当b/f＜1时:

接触线的条数n为

n=fix(b(tan αb+f)/pt)+1.

啮合面的宽度f范围内的接触线的条数m为

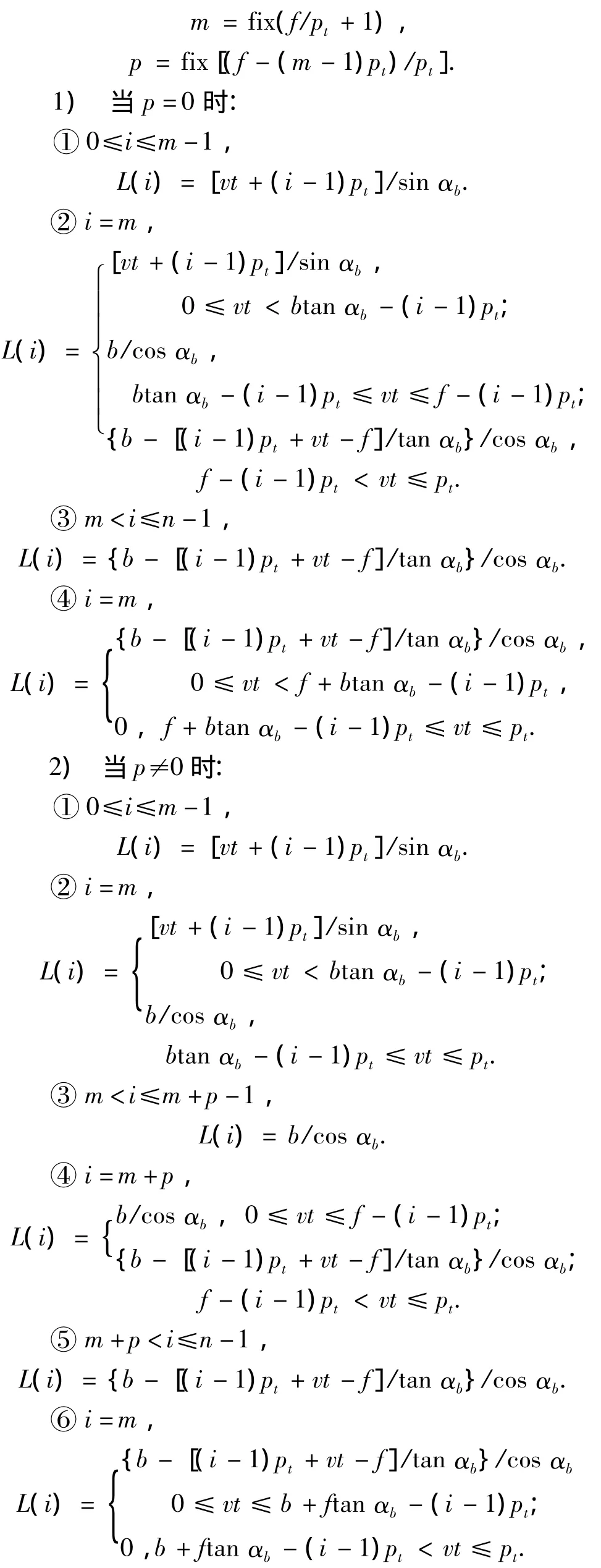
情况3 当b/f=1时:

接触线的条数n为

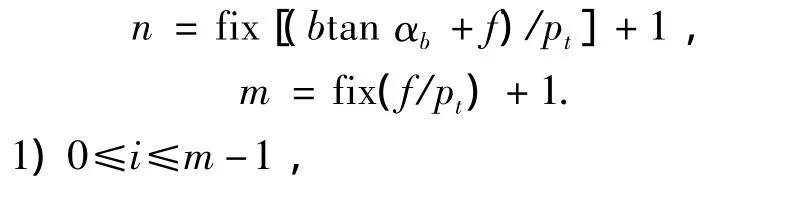
式中:αb为基圆螺旋角，(°);pt为端面齿距，mm;f为啮合面的宽度，mm;b为斜齿轮的宽度，mm;v为节圆表面速度，m/s.

接触线的总长度为

2 计算结果和分析

文献［11］提供的斜齿轮参数代入到本文算法中计算结果对比如图2所示，计算结果与文献结果基本一致，初步验证算法正确.

图2 结果对比Fig.2 The diagramof comparison result

螺旋角是斜齿轮重要的特征参数，也是引起接触线变化的主要因素.以某齿轮箱内的一对外啮合斜齿轮副为例计算，其参数如表1所示.当螺旋角β无限趋于0(β→0)，即接近为直齿轮，采用本文算法计算其接触线变化，如图3所示.

表1 斜齿轮副参数Table 1 The parameters of gear pair

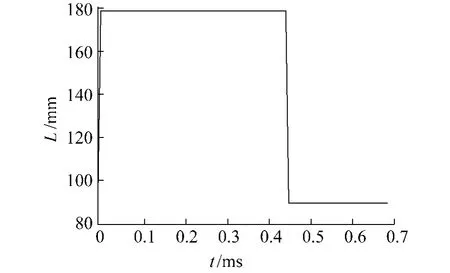
图3 直齿轮接触线长度变化Fig.3 Dependence of contact length on time of spur gear

直齿轮重合度在1～2之间，由于齿宽为90 mm，双齿接触时接触线长度180 mm，单齿接触时接触线长度为90 mm.符合直齿轮在一个端面齿距内的接触线变化规律.

在螺旋角常用范围 10°～30°内选择 10°、15°、20°、25°、30°，用本文算法计算在一个端面齿距运行时间内接触线总长度变化情况，如图4所示.

图4 不同螺旋角时变接触线总长变化Fig.4 Dependence of contact length on time with different helix angles

采用AutoCAD几何画图量取不同螺旋角下一个端面齿距内的接触线长度变化，把端面齿距分为10个等分点，量取这10个点对应的接触线总长度L，结果如图5所示.

本文程序与几何验证的最大值、最小值以及均值如表2.

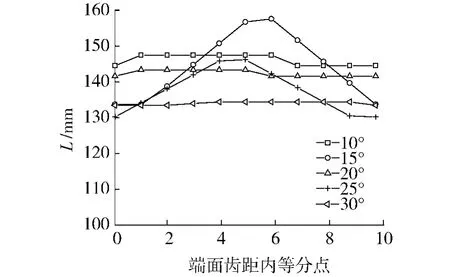
图5 几何测量端面齿距内接触线Fig.5 Contact length by geometric measurement in a transverse pitch

表2 几何测量值与程序值对比Table 2 The comparison result of measured values and procedure values

由于计算机在计算过程中对结果小数点后的位数多次取舍导致与测量结果稍有不同，但基本一致，再次验证程序准确.采用中国航空工业标准HB/Z84.2-1984［12］中斜齿轮接触线计算方法算出接触线均值与本文的计算结果对比如表3，结果显示本文计算接触线总长的平均值与标准计算的平均值相比误差在5%以内，此算法精度可靠.计算不同螺旋角下的接触线均方根值(RMS)变化规律如图6所示.

表3 与HB/Z84.2－1984计算结果比较Table 3 Result comparison with HB/Z84.2-1984

图6 不同螺旋角接触线均方根值Fig.6 The rootmean square of contact line length with different helix angles

从图6中可知，在螺旋角10°～30°内，随着螺旋角的增大，接触线长度的均方根值变小.这是因为螺旋角变大，轴向重合度变大，端面重合度变小，整体重合度是变大的.但是，随之带来啮合面的宽度变小，基圆压力角变大，端面齿距变大导致接触线的条数变少，长度变短，使得整体上接触线的总和变小.

接触线的波动会带来较大的振动和噪声，计算不同螺旋角的接触线最大值与最小值的幅值变化情况，其变化规律(波动率V)如图7所示.

图7 不同螺旋角接触线波动率Fig.7 Volatility of the length of contact line with different helix angles

图7 表明，螺旋角为 15°时波动最大，20°、30°时候波动最小.如图1所示，初始时刻当L1和L3的最大值(端面齿距)相等，且L2和L4的大小相等时，整个接触线是没有变化的，齿轮运行最平稳.这是因为随着L3的增加第1条接触线变长，第n条接触线变短，2条接触线变化量相等，对整个接触线总长度变化不起作用.第i条接触线增加，第j条接触线长度变短，二者变化量相等对整个接触线总长度变化没有影响.表4为初始时刻各螺旋角的L1、L2、L3(端面齿距)、L4的值.

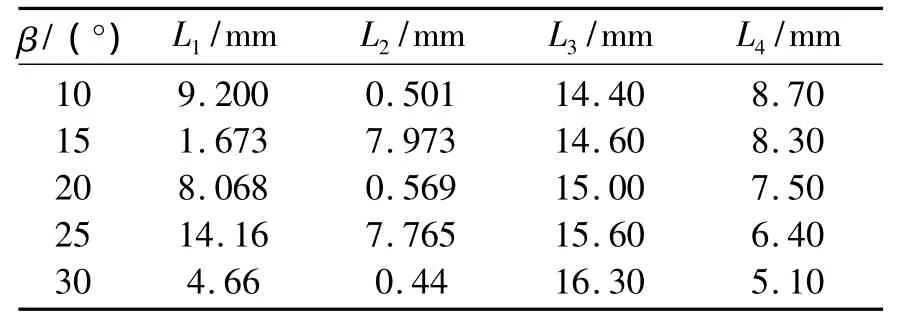
表4 啮合面内接触线的位置参数Table 4 The contact line position parameters in the pressure plane

螺旋角为15°时的波动最大，这是因为L3的长度远大于L1的长度，L2和L4的长度接近使得第1条接触线一直增大从而使接触线总长度急剧正增大，使得波动值也较大.20°、30°的波动较小是因为L1和L4长度相近，当第n条接触线的移出接触区后，第i条接触线过了C点其长度在一段时间内是不变化的.第j条接触线长度减少，第1条接触线长度增加，增加量和减少量相等使得整个接触线长度变化较小，其波动也就小.虽然L1与L3、L2和L4较为相近，但还有一定差距，导致25°的螺旋角齿轮的接触线还有一定的波动.

3 结论

1)本文突破了接触线数值计算所受条件限制，扩大了数值计算接触线的应用范围，算法简单实用.

2)与航空工业标准(HB/Z84.2-1984)计算结果对比显示，误差值在5%以内，本算法有效可靠.

3)分析了螺旋角对斜齿轮接触线长度均方根值的影响，在端面齿距内随着螺旋角的增大，接触线长度均方根值变小.

4)时变接触线波动受到啮合面内初始时刻接触线位置影响，本文给出接触线波动最小的条件:初始时刻当L1和端面齿距相等，且L2和L4相等时，整个接触线没有波动，齿轮运行最平稳.

［1］PAREY A TONDON N.Spur gear dynamic models including defects:a review［J］.The Shock and Vibration Digest，2003，35(6):465-478.

［2］WANG J，LIR.PENG X.Survey of non-linear vibration of gear transmission systems［J］.Applied Mechanics Review，2003，56(3):309-329.

［3］VELEX P，SAINSOT P.An analytical study of tooth friction excitations in errorless spur and helical gears［J］.Mechanismand Machine Theory，2002，37(7):641-658.

［4］MAATAR M，VELEX P.An analytical expression for the time-varying contact length in perfect cylindrical gears:some possible applications in gear dynamics［J］.Journal of Machine Design，1996，118(4):586-589.

［5］BORNER J，HOUSER D R，Friction and bendingmoments as gear noise excitations［J］.SAE Transaction，1996，105(6):1669-1676.

［6］VELEX P，CALIOUET V.Experimental and numerical investigations on the influence of tooth friction in spur and helical gear dynamics［J］.Journal of Mechanical Design，2000，122(4):515-522.

［7］LUNDVALL，STROMBERG N，KLARBRING A.A flexible multi-body approach for frictional contact in spur gears［J］.Journal of Sound and Vibration，2004，278(3):479-499.

［8］VAISHYA M，SINGH R.Strategies formodeling friction in gear dynamics［J］.Journal of Mechanical Design，2003，125(2):383-393.

［9］KUBO A，KIYONO S.Vibration excitation of cylindrical involute gears due to tooth formerrors［J］.Bulletin of JSME ，1980，23(183):1536-1543.

［10］SMITH JD.Gears and their vibration［D］.NewYork:Marcel Dekker，1983:102-156.

［11］CHINMAYA K，MOHANTY A R.An algorithmfor determination of time-varying frictional force and torque in a helical gear system［J］.Mechanismand Machine Theory，2007，42:482-486.

［12］中华人民共和国航空工业部.HB/Z84.2-1984航空渐开线圆柱齿轮齿面接触疲劳强度计算［S］.中国标准出版社，1985.