基于在线补偿算法的卫星姿态控制系统容错控制

管宇，赵石磊，张迎春，贾庆贤

(1.哈尔滨工业大学卫星技术研究所，哈尔滨150001；2.哈尔滨理工大学软件学院，哈尔滨150040)

随着以完成高精度和高稳定度为航天任务的小卫星概念的提出和应用，对卫星姿态控制系统的可靠性和安全性提出了更高的要求.由于在轨卫星长期工作在失重、高低温等恶劣环境下，而且卫星部件故障具有不可修复性，因此，研究卫星姿控系统的容错控制对提高卫星在轨自主运行可靠性有着重要的理论意义和应用价值.

目前，针对卫星容错控制方法的研究在理论和应用上都取得了一定的研究成果［1-4］.例如，Cai［5］针对受外部干扰作用以及推力器失效故障的航天器姿态跟踪问题，设计了一种自适应姿态容错控制器.Hou［6］基于控制有效因子设计了两级Kalman滤波器的故障诊断系统，实现了对卫星姿态控制系统传感器和执行器故障的有效估计.现有智能容错控制方法大多利用神经网络方法［7-8］，通过对权值的自动调节来实现自适应容错控制，但由于神经网络存在权值在线调节复杂，网络结构难于确定等缺点，在很大程度上限制了其应用.核学习方法［9-10］能逼近任意非线性函数，且能够利用所谓的“核技巧”通过内积运算来越过非线性映射，从而避免了维数灾难以及因“降维”所导致的性能下降问题，已被广泛地应用于非线性系统参数辨识、控制等领域，也为非线性故障的诊断及容错控制提供了新的途径.

文献［11］采用内模控制原理，给出了多状态时滞系统的容错控制器设计方法，但没有考虑非线性情况下的容错控制问题.文献［9］将多核学习支持向量机方法应用于变压器故障诊断，但没有进一步考虑故障的补偿.本文针对卫星模型存在的非线性和外部干扰特性，考虑传感器和执行机构存在故障的姿态控制问题，在充分利用星上硬件冗余条件基础上，提出一种将在线核学习方法与自适应内模控制相结合的容错控制方法.该方法在继承自适应内模控制优点的同时，引入了一种基于正交匹配追踪思想的在线核学习算法，利用所提出的在线学习算法来补偿原系统的逆模型，有效地保证了故障后原系统与补偿后的逆模型保持逆的关系，使得故障后系统能够有效地跟踪输入信号，达到自适应容错控制的目标.最后，将该方法应用于卫星的姿态控制.

1 自适应容错控制策略

卫星非线性动力学模型方程为

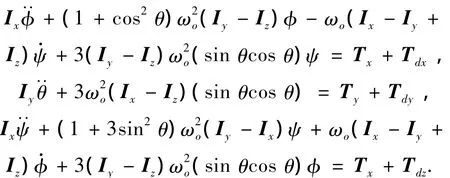
式中:φ、θ、ψ分别为参考坐标系的3个姿态角:滚转角、俯仰角和偏航角，ωo为轨道角速度，Ix、Iy、Iz为各轴的转动惯量，Tx、Ty、Tz分别为3个轴上的控制量，即执行机构产生的控制力矩，Tdx、Tdy、Tdz分别为3个轴上的外部干扰力矩.

考虑非线性系统u(t)=［TxTyTz］T∈R为系统输入，y(t)=［φ θ ψ］T∈R为系统输出，R为有界紧集，系统输入输出阶次分别为m和n(m≤n).则动力学模型可描述为

式中:F(g)是定义在R上关于各变量连续的非线性函数，且满足线性增长性条件，即存在正常数ηi(1≤i≤m+n)使下式成立.

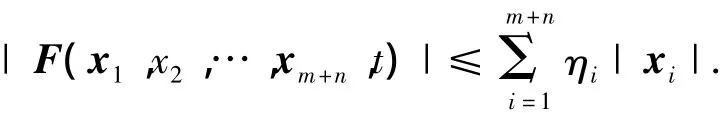
1.1 系统结构

针对由微分方程描述的卫星非线性系统，先利用在线核学习算法求得其逆系统，再将逆系统与原非线性系统复合成伪线性系统引入内模控制中，实现故障后系统的自适应容错控制.系统结构如图1所示，其中内模控制中内部模型为理想的α阶积分环节，内模控制器为滤波器与模型逆的乘积，伪线性系统的输入为u，输出为y*，闭环系统的参考输入为r，输出为y，d为干扰力矩.基于核学习算法的在线补偿模块用于辨识系统发生故障时产生的变化:无故障时，误差值小于算法所设定的门限，辨识算法不启动.故障发生时，逆系统与原系统输出之间的误差变大，核学习算法利用力矩差值作为目标函数进行在线学习，对故障状况下的系统进行补偿.

图1 基于在线补偿的IMCFig.1 IMC based on online compensation

1.2 鲁棒稳定性研究

设图1中伪线性系统的传递函数为G(s)，内部模型为Gm(s)，内模控制器为GIMC(s).由于非线性建模误差的存在，G(s)可看成若干线性定常系统组成的模型集合π，在频域中可描述为

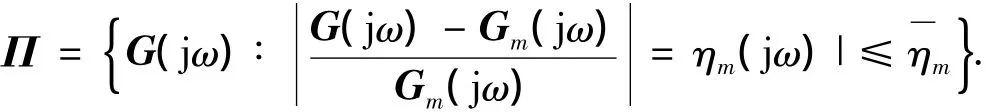
引理1 对于单位负反馈控制系统，具有建模误差的被控对象传递函数为 Gp(s)，其模型为Gm(s)，控制器传递函数为Gc(s)，则保证闭环系统稳定的充要条件为

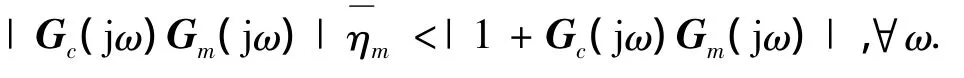
定理1 对于图1所描述的内模控制系统，保证闭环系统稳定的充要条件为

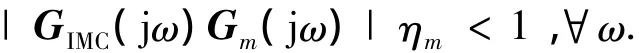
证明:由图1可知系统的闭环传递函数为

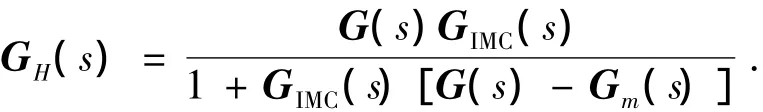
其等效开环传递函数为

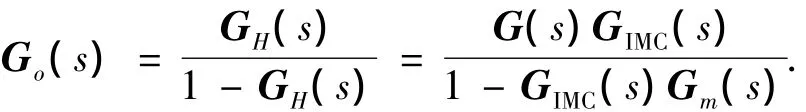
从而，可以得到单位负反馈系统控制器的传函:

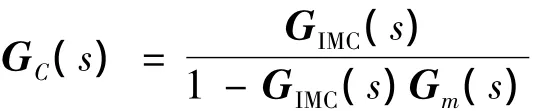
式(1)由引理1可得

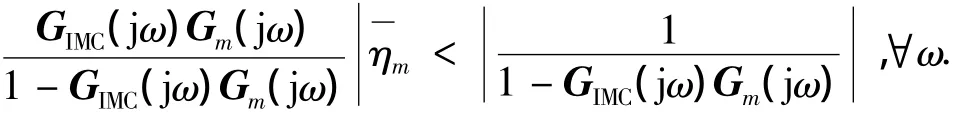
显然可得

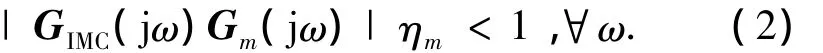
证毕.

本文所设计的自适应容错控制系统中的内模控制器为GIMC(s)=F(s)(s)，代式(2)有

2 基于在线补偿算法的伪线性系统

当卫星系统出现故障后，系统模型发生未知变化，要精确求得系统的逆模型难以实现.本文提出了一种基于正交匹配追踪的在线核学习算法，通过输入输出样本辨识出逆系统的结构，对故障后逆系统进行补偿.

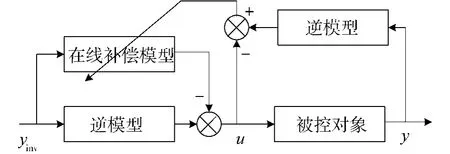
图2 基于在线补偿的辨识结构Fig.2 Identification structure based on online compensation

2.1 α阶积分逆系统

假设非线性系统Σ:u→y的动力学模型可用一个输入到输出的非线性映射算子θ表示为

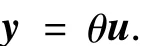
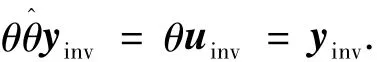
式中:yinv为可微函数为逆映射算子.

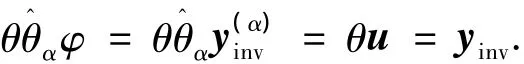
本文采用基于正交匹配追踪的在线核学习算法补偿故障后伪线性系统的α阶积分逆系统.

2.2 正交匹配追踪算法

假设H为信号空间，集合D为N维希尔伯特空间中的向量集合，定义目标函数f∈H的一个最优估计为［，通过参数 αn，gγn∈D 的选择使残差函数‖f－~f‖最小化.匹配追踪就是在集合D中寻找最能准确表示f内积结构的子集来线性表示f函数，利用D在空间上的正交映射来连续估计f函数.对于f的k阶模型可分解为

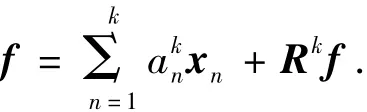
式中:Rkf表示第k次估计后的残差.

由k阶估计模型更新到k+1阶时，表示为

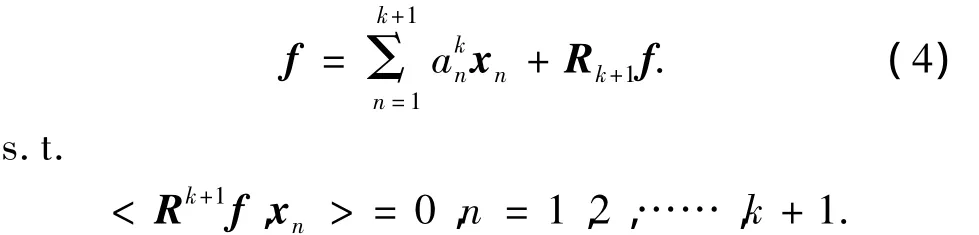
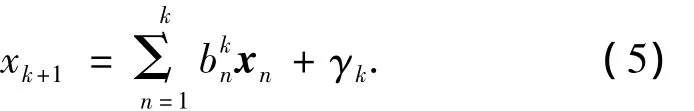
式中:＜γk，xn＞ =0，n=1，2，…，k.

利用辅助模型方程(5)，可以表示由k阶模型，更新到k+1阶估计模型的形式，且表示为

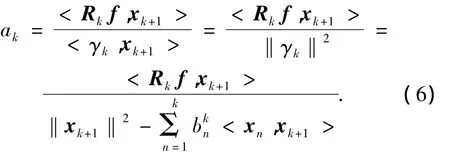
匹配追踪算法的思想是寻找xnk+1∈D/Dk，使得

如果|＜Rkf，xnk+1＞ |＜δ，δ＞0，则算法终止.辅助方程中bk可以通过求解方程Vk=Akbk获得，δ＞0确保了Ak的非奇异性，可得bk=(Ak)－1Vk，其中

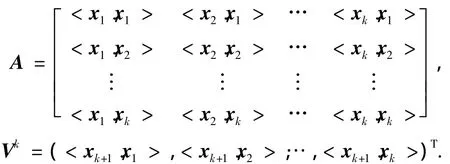
2.3 基于正交匹配追踪的在线核学习补偿算法

将在线核学习方法引入正交匹配追踪算法可以分解成以下3个问题:

2)基向量的取舍:使新样本加入集合Dk中的计算的问题.当一个新的样本被观测到后，由于在线算法在每个时刻获得的观测量不可能都与集合Dk中的向量正交，因此这里分2种情况来求解

情况1 新观测样本xk+1经映射后不能被集合Dk中的映射样本{φ(x1)，φ(x2)，…，φ(xs)}线性表示，即 ＜ γk，φ(xn)＞ ，γk≠0 时.式中:表示系数向量n=1，2，…，k.

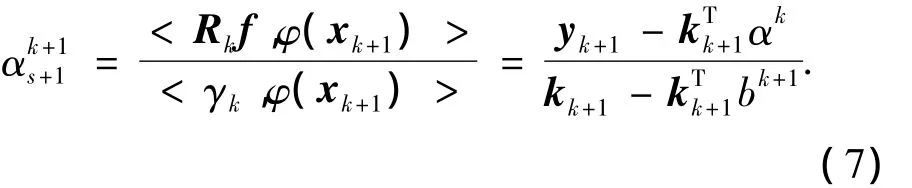
情况2 新观测样本xk+1经映射后的φ(xk+1)能够被集合Dk中映射样本{φ(x1)，φ(x2)，…，φ(xs)}线性表示，即 γk≈0 时，根据 Backfitting 算法［13］，需要对整个表达式进行更新，更新式可以写成:

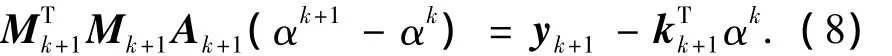
3)核矩阵的递归计算:为了能够减少在线计算量，这里给出2种情况下核矩阵的迭代方程，以减少在线计算量.根据上述的2种情况:

情况1 新观测量xk+1映射后的φ(xk+1)能线性表示，不需要更新集合 Dk时，(Ak+1)－1=(Ak)－1.

情况2 新观测量xk+1映射后的φ(xk+1)不能线性表示时，即Ak+1≠Ak，可通过下面的公式迭代计算得到(Ak+1)－1:

综合上述分析，基于正交匹配追踪的在线核学习算法可表述为:

初始化:选取参数 v，δ(v，δ＞0)，令

1)获得新样本(xk+1，yk+1);

2)如果|＜Rkf，xk+1＞ |＜δ，返回1)，获取新本;否则，计算 bk+1=(Ak)－1kk+1，δk+1=~kk+1－

若 δk+1＜ v，则按照式 (7)计算 αk+1，且(Ak+1)－1=(Ak)－1，Dk+1=Dk;

否则，按照式(8)计算 αk+1，并更新(Ak+1)－1，Dk+1=Dk∪{xk+1}.

3)返回1)，获取新样本.

3 容错控制仿真结果与分析

为了验证本文中提出的自适应容错控制方法的有效性，将在线补偿的伪线性系统引入到内模控制中，并应用Matlab/Simulink软件分别对系统传感器和执行机构故障进行了仿真分析，卫星的转动惯量为 Ib=diag(1.977，2.466，2.577)，kg·m2.卫星的执行机构选为反作用飞轮，且外部干扰力矩分别为Tdx=A0(3cosω0+1)，Tdy=A0(1.5sin ω0t+3cosω0t)，Tdz=A0(3sin ω0t+1)，其中，A0=1.5 ×10－5N·m为干扰力矩幅值.卫星初始值设定为ω0=0.001 105 8，rad/s初始角度误差为［－0.18，－0.74，0.22］，rad; 初 始 角 速 度 误 差 为［0.008 727 8，－0.009 831 3，－0.004 362 2］，rad/s.

由于涉及的故障为时间t的函数，因此输入中加入了时间因素并对输入输出进行归一化处理，且选取高斯核函数的宽度取为σ=1，在线辨识方法参数选为 δ=0.001，v=0.001.另外，内模控制中的滤波器选取二型滤波器，为了减小控制量，滤波器参数设置为λf=1，使系统能够完全抑制阶跃和斜坡扰动.

3.1 传感器故障下容错控制仿真结果

假设x轴传感器在t=100 s时姿态角发生大小为1 rad阶跃型故障，而其他传感器正常工作，仿真结果如图3所示.

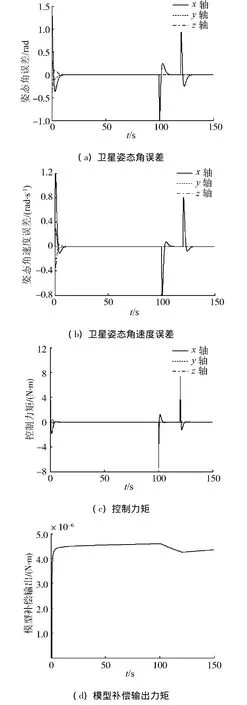
图3 传感器故障下容错控制仿真结果Fig.3 Simulation results of fault-tolerant control system with sensor failure

可见，x轴传感器发生故障时，由于采用内模控制方法，系统能够自适应地调节传感器故障，故障消失后，系统仍能有效跟踪输入，故障并不影响输出，因此不需要在线补偿调整.

3.2 执行机构故障下容错控制仿真结果

假设x轴反作用飞轮在t=50∶150 s时发生大小为0.5 sin t(N·m)的故障，而其他反作用飞轮正常工作.由于考虑的执行机构故障为非线性故障且为时间t的函数，因此，仿真中在线辨识模型的输入部分加入了时间因素，仿真结果如图4所示.可见，执行器发生故障时，逆模型已不能正确表示故障后的系统逆模，造成输出偏差较大，在线补偿算法启动，对系统逆模型误差进行补偿，补偿后的系统能够有效跟踪输入，卫星的指向精度降低于0.2°.

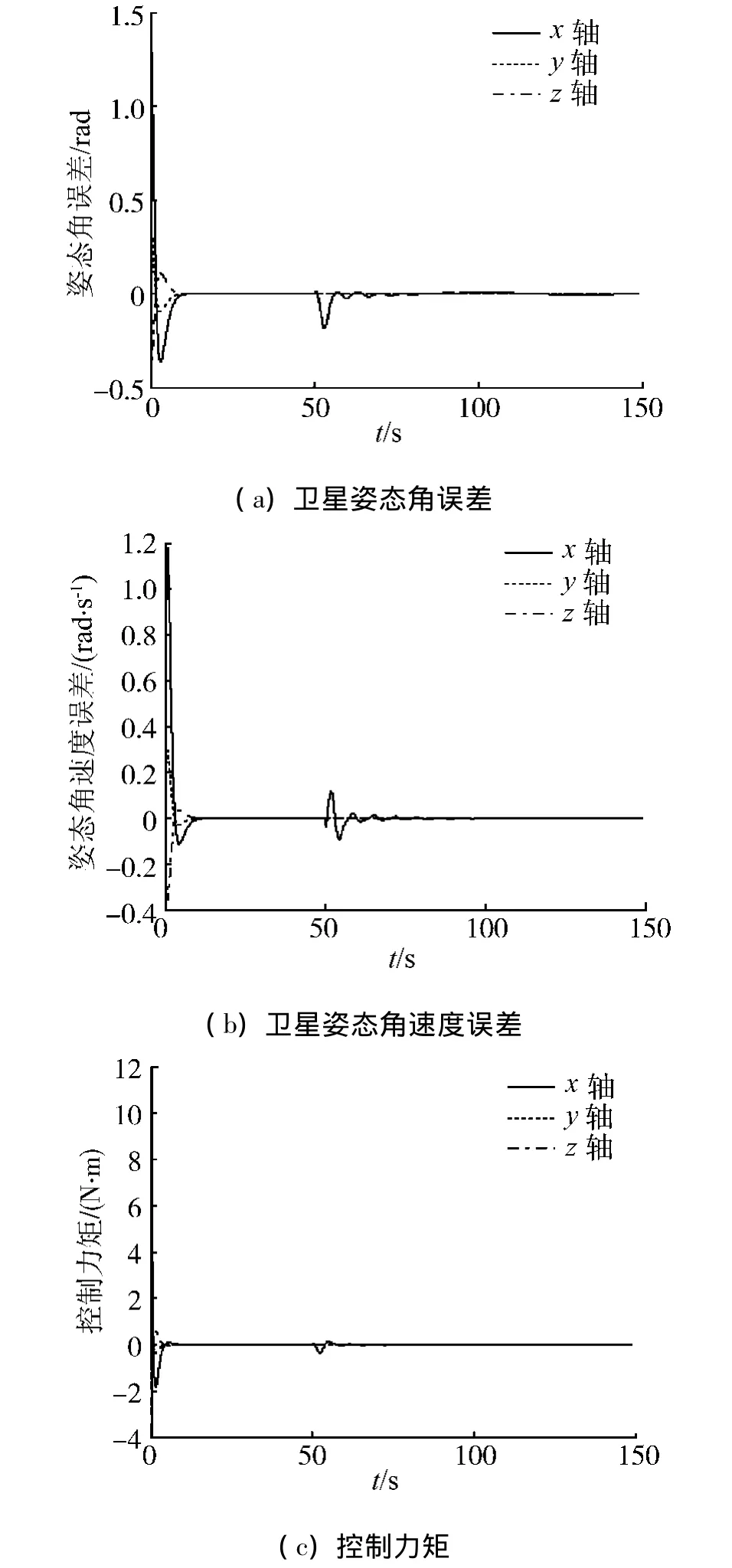
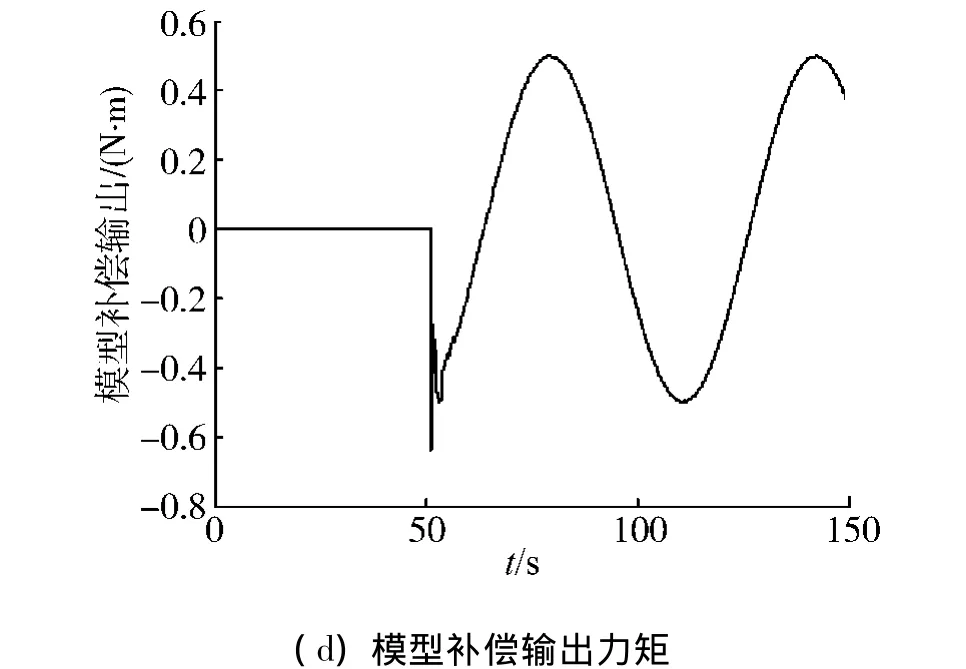
图4 执行机构故障下容错控制仿真结果Fig.4 Simulation results of fault-tolerant control system with actuator failure

4 结束语

针对卫星存在外部干扰力矩影响和传感器、执行机构存在失效故障的问题，本文提出了一种基于在线核学习算法补偿的自适应容错控制方法.该方法通过辨识干扰所造成的模外动态误差，可有效补偿故障后系统的逆模型，使之能够准确地表达故障系统的逆.并且，将故障后逆模型与原系统组成的伪线性系统引入卫星姿态系统的内模控制进行仿真验证，仿真结果表明该方法在保证系统一定性能品质的情况下，能够实现故障的容错控制，具有一定的应用前景.

［1］GAO Z F，JIANG B，SHI P.Sensor fault estimation and compensation for microsatellite attitude control systems［J］.International Journal of Control Automation and Systems，2010，8(2):228-237.

［2］JIN J，KO S，RYOO C K.Fault tolerant control for satellites with four reaction wheels［J］.Control Engineering Practice，2008，16(10):1250-1258.

［3］VARMA S，KUMAR K D.Fault tolerant satellite attitude control using solar radiation pressure based on nonlinear adaptive sliding mode［J］.Acta Astronautica，2010，66(3):486-500.

［4］HENRY D.Fault diagnosis of microscope satellite thrusters using H-infinity/H-filters［J］.Journal of Guidance，Control，and Dynamics，2008，31(3):699-711.

［5］CAIW C，LIAO X H，SONG Y D.Indirect robustadaptive fault-tolerant control for attitude tracking of spacecraft［J］.Journal of Guidance，Control，and Dynamics，2008，31(5):1456-1463.

［6］HOU Q，CHENG Y H，LU N Y，et al.Study on FDD and FTC of satellite attitude control system based on the effectiveness factor［C］//2nd International Symposium on Systems and Control in Aerospace and Astronautics.Shenzhen，China，2008:1096-1101.

［7］朱大奇，孔敏.基于平衡学习的CMAC神经网络非线性滑模容错控制［J］.控制理论与应用，2008，25(1):81-86.ZHUDaqi，KONGMin.Fault-tolerant controlofnonlinear system based on balanced learning CMAC neural network［J］.Control Theory＆ Applications，2008，25(1):81-86.

［8］赵峻，孙伟，王雪松.基于神经网络的非线性系统轨迹线性化自适应容错控制［J］.控制与决策，2011，26(6):902-906.ZHAO Jun，SUNWei，WANG Xuesong.Adaptive fault-tolerant control of nonlinear systems using trajectory linearization based on neural network［J］.Control and Decision，2011，26(6):902-906.

［9］尹玉娟，王媚，张金江，等.一种自主核优化的二值粒子群优化-多核学习支持向量机变压器故障诊断方法［J］.电网技术，2012，36(7):249-254.YIN Yujuan，WANGMei，ZHANG Jinjiang，et al.An autonomic kernel optimization method to diagnose transformer faults bymulti-kernel learning supportvector classifier based on binary particle swarm optimization［J］.Power System Technology，2012，36(7):249-254.

［10］SONG H Z，ZHONG L，HAN B.Structural damage detection by integrating independent component analysis and support vector machne［J］.International Journal of Systems Science，2006，37(13):961-967.

［11］吴军生，翁正新，田作华，等.基于广义内模控制的时滞系统主动容错控制设计［J］.上海交通大学学报，2009，43(3):417-421.WU Junsheng，WENG Zhengxin，TIAN Zuohua，et al.Active fault tolerant control design for time-delay systems based on generalized internal model control［J］.Journal of Shanghai Jiaotong University，2009，43(3):417-421.

［12］PATIY C，REZAIIFAR R.Orthogonal matching pursuit:recursive function approximation with applications to wavelet decomposition［C］//Proceedings of the Twenty-seventh Asilomar Conference on Signals Systems and Computers.Pacific Grove，USA，1993，40-44.

［13］PASCAL V，YOSHUA B.Kernel matching pursuit［J］.Machine Learning，2002，48(1/2/3):165-187.