基于惩罚最小二乘估计的长期用电量半参数预测模型
2012-09-03王晓佳刘辉舟
邵 臻,王晓佳,高 飞,刘辉舟,杨 露
(合肥工业大学a.管理学院;b.过程优化与智能决策教育部重点实验室,合肥 230009)
基于惩罚最小二乘估计的长期用电量半参数预测模型
邵 臻,王晓佳,高 飞,刘辉舟,杨 露
(合肥工业大学a.管理学院;b.过程优化与智能决策教育部重点实验室,合肥 230009)
文章针对惩罚最小二乘估计的高精度特性,构建了基于惩罚最小二乘估计的半参数回归模型。并将指数平滑思想融入模型,对模型的误差序列进行趋势外推与大幅度外延预测。实证结果表明了所提方法的有效性。
半参数模型;惩罚最小二乘估计;指数平滑;电量预测
0 前言
目前,长期负荷预测领域的研究方法主要包括参数理论与非参数理论等[1~3]。状态空间、回归分析、神经网络、灰色理论、支持向量机和最优组合预测方法等,基本上都属于参数统计法的范畴,因变量对自变量有较强的依赖关系,当假设函数模型成立时,预测精度较高,当假设函数不成立时,预测模型的拟合情况和预测精度都不理想。非参数理论降低了自变量对因变量的限制,有较大的适应性,但也可能会失去历史资料所提供的信息,降低模型的解释能力。
传统的参数回归操作简便,可以外延,适于预测,但难以精确拟合复杂的曲线;非参数回归形式灵活,可以精确拟合复杂曲线曲面,但难以进行大幅度外延预测。半参数模型最早由Stone于1977年提出,它有线性主部,可以把握大势走向,适于外延预测;还有非参数部分,可以作局部调整,使数据较精确地拟合。半参数模型引入了非参数,克服了传统偏差函数模型的局限性,使得数学模型与客观实际更为接近,在数值上能够分别求出参数、非参数(模型误差)和偶然误差,是一种非常理想的数据处理方法。本文拟对传统半参数模型进一步改进,改进后的半参数模型将指数平滑法融入模型并结合惩罚最小二乘估计法进行参数估计,目前在电力负荷预测领域半参数模型的应用尚不多见,将其运用于电力负荷预测领域,将改善传统方法诸如无法适应较大幅度外延预测要求、预测精度偏低等不足之处。
1 模型构建
1.1 半参数模型
半参数模型一般形式为:
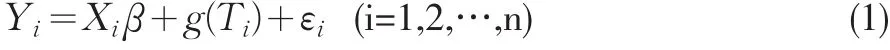
其中yi是因变量;xi是参数部分自变量;Tj是非参部分自变量;β是回归系数,即待求参数;g为定义于实数集上的未知函数;ε是随机误差,E(ε)=0,E(ε2)=σ2。xiβ反映了负荷预测可知的部分规律,把握因变量y变化的趋势走向,为参数部分;g(Ti)+εi反映了负荷预测的不确定因素的影响,为非参数部分。
1.2 惩罚最小二乘法则
半参数回归模型的估计方法很多,常见的有两阶段法、核函数法、样条法、最近邻法等等[4,5]。本文为了达到既可以排除随机误差项产生的噪音,同时又使得解具有一定的光滑性,从而有利于数据拟合以及外延预测的目的,采用基于惩罚最小二乘估计的半参数回归模型。
惩罚最小二乘准则函数为[6]:
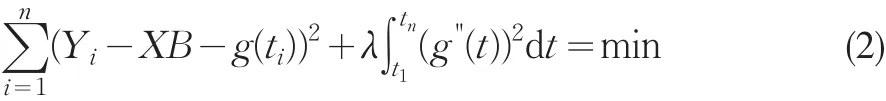

当λ→0时,g(t)趋近于观测量的三次样条内插。当λ→∞时,g(t)趋近于观测量的线形回归。可证明惩罚最小二乘原理的惩罚项可以表达为(Fessler,1991):

其中,Q与T是 n×(n-2)和 (n-2)×(n-2)的矩阵。令 hi=ti+1-ti,i=1,2,…,n-1。
Q中元素满足:
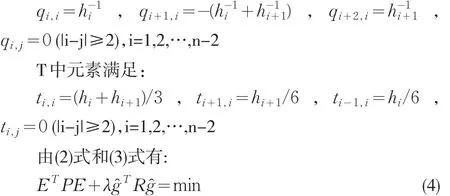

最终可以得到迭代求解方程,令

由式(6)、式(7)可计算 gˆ和 Bˆ,观测值的估计为:

1.3 基于三次指数平滑法的误差修正
对于模型(10)我们还无法直接进行外推预测,对于误差时间序列项gˆ我们需要作进一步处理。由函数逼近论可知,对于足够光滑的函数我们可以用多项式函数去逼近。
设误差序列项{gˆn}具有二次多项式趋势,在二次指数平滑序列的基础上,再做三次指数平滑序列:

2 模型求解
2.1 光滑参数λ的确定
光滑参数λ的取值对参数,特别是对惩罚项估值的影响很大,其取值好坏将直接影响到实际拟合效果。当平滑参数值λ选取较大时,λ的取值对数据平滑问题来说是十分关键的。
目前在平滑参数的选取准则很多[7]。一些是基于再抽样方法,例如CV,GCV准则等等;而另一些是基于模型复杂度惩罚方法,例如基于AIC,BIC准则的选择方法。虽然几类方法的形式不同,本质上都是为了寻找合适的参数,使得模型具有较优的预测性能和泛化性能。
(1)交叉核实准则
交叉核实(cross-validation,CV),其基本思想是:选取λ所得的拟合曲线,用此曲线进行预测,使所有预测点的均方误差最小。在应用时,常常将(xi,yi)模拟为预测点(即去掉此点),而依据剩下的n-1个点进行估计,再将(xi,yi)代入所拟合的曲线,得到此点的值,记为Yˆi。于是我们定义交叉核为:

其中,hii(λ)为帽子矩阵 H(λ)中的元素,使 CV(λ)值最小的λ即为所求值。
(2)广义交叉核实准则
广义交叉核实法(Generalized Cross-Validation,GCV)是Leave-one out cross-validation方法的近似,我们定义广义交叉核为:

2.2 模型预测
本文采用循环预测法进行负荷预测[8,9],其基本思想是:对每一次的负荷预测值进行循环使用。对于半参数回归模型,当预测yn+1时,利用三次指数平滑预测技术对gˆ(n+1)进行估计,得到负荷预测值 yˆn+1 ,将负荷预测值yˆn+1添加到原负荷样本(y1,y2,…,yn)中组成新负荷样本(y1,y2,...,yn,yˆn+1),再采用前述半参数估计方法进行等间隔的下一步预测,如此循环直至得到所需的p步预测值。
3 算例分析
3.1 自变量的选取
影响电力负荷消耗的因素很多,例如经济增长水平、经济发展阶段、经济结构特性以及生产生活水平等等诸多影响和制约因素。具体选取了全社会固定资产投资总额、国内生产总值、人均国内生产总值、工业增加值、社会消费品零售总额、人口数量、商品零售价格指数、工业总产值等因素。计算自变量、因变量之间的相关程度,并去除与因变量相关程度较小的影响因素。
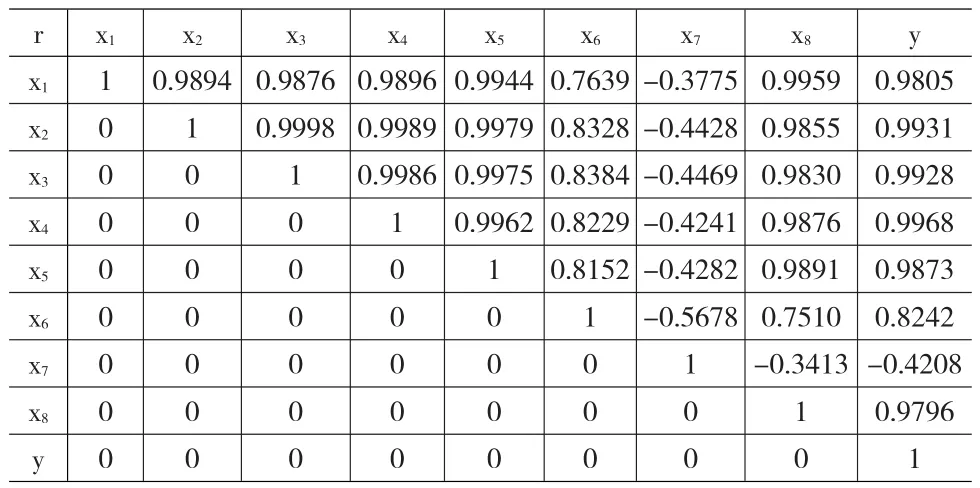
表1 自变量、因变量间的相关系数
通过灰色关联度理论,计算出诸多影响因素(自变量)与因变量之间的灰色关联度,对于所选取的8个影响因素其灰色关联度依次为:0.9088,0.7243,0.6201,0.8762 ,0.9298,0.6495,0.9418,0.6082。综合相关系数和灰色关联度理论选取全社会固定资产投资总额、工业增加值、社会消费品零售总额3个影响因素并进行单位根检验,自变量与3个影响因素在5%的置信水平下可以认为不存在单位根,因此选取上述3个因素建模。
3.2 算例分析
本文收集了1985~2009年江苏省年度全社会用电量及其影响因素的资料。电量单位为亿kWh,人口单位为万人,产业值单位为亿元。影响年用电量(自变量)的因子有GDP,全社会固定资产投资总额,工业增加值,社会消费品零售总额,总人口数。用1985~1999年资料建模,2000~2009年资料进行检验。
对于光滑参数λ的选取,本文采用广义交叉核实法(Generalized Cross-Validation,GCV)。通过GCV法迭代选取,最终选择λ=0.43时达到较好的逼近精度和预测效果。

表2 拟合和检验结果

表3 拟合和检验结果
通过表2预测结果的对比不难发现,基于惩罚最小二乘估计的半参数模型在参数拟合阶段表现出了很高的精度。通过对原始数据良好的拟合,从而反映原始数据的变化趋势,同时结合三次指数平滑法进行趋势外推,从而进行预测。由表3可知基于惩罚最小二乘估计法的误差指标是比较令人满意的。基于惩罚最小二乘估计的半参数模型进行用电负荷预测具有较高的预测精度和实用性,半参数模型相较于传统用电负荷预测模型具有更高的预测精度。
4 结束语
比较计算结果可以看到:在进行较大幅度全社会用电量需求外延预测时,半参数回归法估计的平均拟合误差远远小于灰色GM(1,1)、多元线性回归等传统方法。说明半参数模型对电力需求预测估计精度较高。通过数值的拟合计算结果显示,拟合估计值也比较接近真实值。也再次证明半参数模型对电量需求预测估计的优越性。
文中主要考虑经济增长水平、经济发展阶段、经济结构特性以及生产生活水平等等诸多影响和制约因素,然而实际中用电负荷的需求还受到其它因素的影响,如自然因素等。在今后的研究中,应进一步分析各种因素对用电负荷的影响,建立更精确的预测模型。同时半参数预测模型的拟合步长和预测步长的选取也是值得进一步研究的问题。
[1]牛东晓,曹树华等.电力负荷预测技术及其应用[M].北京:中国电力出版社,2009.
[2]康重庆,夏清,张伯明.电力系统负荷预测研究综述与发展方向的探讨[J].电力系统自动化,2004,28(7).
[3]邰能灵,侯志俭,李涛,蒋传文,宋炯.基于小波分析的电力系统短期负荷预测方法[J].中国电机工程学报,2003,23(1).
[4]叶阿忠.非参数计量经济学[M].天津:南开大学出版社,2003.
[5]Jan G,De Gooijer,Daw it Zerom.Kernel-based Multistep-ahead Pre⁃dictions of the US Short-term Interest Rate[J].Journal of Forecasting,2000,19(4).
[6]高宁,高彩云,徐长海.补偿最小二乘估计在确定高程异常中的应用[J].测绘科学,2011,36(1).
[7]陈建东,李娴,王小明.LS-SVM的GCV模型选择方法与快速算法[J].模式识别与人工智能,2010,30(1).
[8]Stephanie M.Pickle,Timothy J.Robinson,Jeffrey B.Birch,Christine M.Anderson-Cook.A Semi-Parametric Approach to Robust Parame⁃ter Design[J].Journal of Statistical Planning and Inference,2008,138.
[9]Three-Stage Semi-Parametric Estimation of T-copulas:Asymptotics,Finite-sample Properties and Computational Aspects[Z].Computation⁃al Statistics and Data Analysis,2010.
F224
A
1002-6487(2012)24-0026-03
国家自然科学基金资助项目(71071045;70801024)
邵 臻(1986-),男,江苏宿迁人,硕士研究生,研究方向:预测、决策科学与技术。
王晓佳(1982-),男,安徽蚌埠人,博士研究生,研究方向:预测、决策科学与技术。
高 飞(1986-),女,河北沧州人,硕士研究生,研究方向:决策科学与技术。
(责任编辑/亦 民)
