基于顶点重要性骨架图的视点快速选择算法

金 凯，石振锋，牛夏牧

(1.哈尔滨工业大学建筑学院，150001哈尔滨;2.哈尔滨工业大学数学系，150001哈尔滨;3.哈尔滨工业大学计算机科学与技术学院，150001哈尔滨)

近年来，形状分析与处理技术一直是计算机图形学等领域的研究热点，其主要应用包括在计算机三维动画［1-2］、三维模型分割［3］、形状配准与检索［4-5］、骨架提取［6］和曲面重构等.形状的描述与表达是计算机图形学和三维模型可视化研究中的核心问题.然而，给出一种用于定义形状和描述形状的简单而又有效的方法却是非常难的.线形骨架是三维模型的几何与拓扑结构的一维简洁表示方式，已被广泛应用于三维模型的形状分析和处理.

选择一个好的视点将对三维模型的形状分析与处理、图形绘制、场景理解、场景优化布局等具有非常重要的意义.近年来，视点选择已经成为计算机图形学研究中一个非常重要和活跃的分支.国内外许多研究者提出了自动选择视点或视点集序列的方法.Gooch等［7］提出了一个可计算的显著度模型，并用于自动计算三维模型的初始视点集.Vázquez等［8］利用香农熵定义了视点熵，并利用它来评价一个视点的好坏，提出了选择N个最佳视点构成最小最佳视点集，并用于场景理解等应用.受人类视觉系统低层线索的启发，基于人类视觉系统注意力机制.Lee等［9］基于高斯平均曲率，利用中心-周围机制构造滤波器，提出了一种显著度计算模型，用于构建三维模型的感知重要性区域.对于给定的视点，研究者们将在该视点下三维模型中所有可见顶点的显著度之和定义为该视点的重要性.利用基于梯度下降的启发式优化方法，快速地根据视点的重要性来选择最佳视点.Feixas等［10］在已有研究基础上，定义了一种新的基于多边形互信息的三维模型显著度，并建立了统一的信息论框架用于视点选择和显著度应用.然而，网格模型显著度仅能从视觉注意力的角度刻画三维模型局部视觉重要性.因此，显著度不足以描述三维目标的整体拓扑特性，基于显著图的视点选择也不足以用于三维模型的形状分析.

本文首先根据三维模型的骨架定义了一种新的骨架图，用于描述每个顶点相对于最终骨架的重要性度量，然后定义了视点信息量用于视点选择的优先级度量，最后提出了一种基于迭代式子分方式快速选择最佳和最差视点的计算方法.实验结果表明，本文提出的骨架图方法是合理的，基于骨架图的视点信息量度量是可行的，迭代式子分方式能准确、快速地实现最佳和最差视点的选择.

1 三维网格顶点重要性模型

1.1 三维网格模型骨架提取算法

线形骨架为三维模型全局形状和拓扑结构的描述提供了非常有利的一种表示方法.从人类视觉感知理论出发，根据拓扑知觉理论中人类视觉的整体优先原则［11］，线形骨架用于视点选择、形状分析及处理等是可行的.现有的骨架提取方法可以分为两种主要类型:基于体积的和基于几何的骨架提取方法.

三维网格线形骨架提取的本质就是源网格上的每个顶点都将在一定变换下最终变换并聚集到线形骨架上的过程.设源网格M0有N个顶点组成，记为V={vi｜vi∈R3，1≤i≤N}.设:C为变换;Cj为第j次迭代变换.因此，每个顶点vi在每次变换下都将得到新的坐标，记为网格变换序列记为{Mj={Cj(Mj-1).记最终的线形骨架为S=Skel(M0)，则基于收缩变换的线形骨架提取技术的目标就是设计变换C实现快速的提取线形骨架.图1描述了迭代式线形骨架的提取过程.

图1 基于迭代收缩操作的三维网格模型骨架提取方法

Laplacian收缩变换提供了一种快速有效的工具.文献［1］对三维网格模型实施隐式Laplacian光滑化收缩操作获得最终的线形骨架.Cao等［12］基于文献［1］的基础上，在点云数据上提出了一种线形骨架提取算法.本文实现了这两种线形骨架提取算法，图2给出了基于Laplacian光滑化收缩操作得到最终骨架的过程.在本文中选择文献［12］提出的线形骨架提取算法.

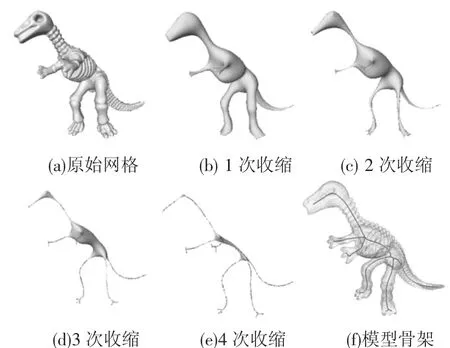
图2 基于Laplacian迭代收缩的三维网格模型骨架提取过程

1.2 三维网格顶点重要性

对于任意给定的顶点vi∈V，第j次收缩变换后的位置为S=Skel(M0)}为顶点v(j)i与最终线形骨架之间的最短距离.在骨架提取过程中，每个顶点将形成距离序列一般来说，该序列是降序并收敛的，因为最终每个顶点都将收敛和变换到线形骨架上，即最终的距离应为0.然而，在迭代变换过程中，顶点vi在源网格M0中的位置对于最终的线形骨架具有非常重要的影响.显然所有顶点vi的相对位置关系即为源模型的拓扑结构，而这种相对位置关系在迭代收缩变换下将收敛到线形骨架.因此，在本文中，定义顶点的重要性为源网格顶点与最终骨架的最短距离，也称为顶点相对于骨架的的初始位移.记顶点vi相对于骨架的重要度为Sig(vi)，则

2 三维网格模型视点快速选择算法

2.1 视点信息量

通常可以认为一个好的视点应该尽可能地提供场景的最大信息，最佳视点将承载该场景中的最大信息量.

给定视点vp，设F(vp)为该视点下所有可见顶点集合，则F(vp)中所有顶点相对于骨架的重要度之和定义为该视点vp可从场景中获得的最大信息量.记最大信息量为Sigsum(vp)，则

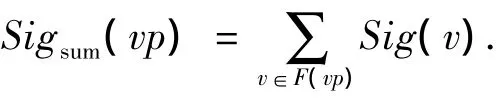
其中:最佳视点vpbest和最不利视点vpworst分别定义为

求解最佳视点vpbest和最不利视点vpworst的方法很多，其中一种可能就是枚举所有视点后，从中选择最大和最小值分别对应的视点作为最佳和最不利视点.然而，这将非常费时，尤其是三维模型的顶点数较多时.在本文中提出了基于迭代求精方式快速获取最佳和最不利视点的方法.

2.2 三维网格模型视点快速选择算法

为提高获取最佳视点和最不利视点的计算效率，本文基于迭代方式逐步求精地选择最佳视点和最不利视点.算法具体描述为:

1)在三维模型的三角化包围球或立方体包围盒上任意采样N个顶点作为初始视点.如果以包围球采样，则通常尽可能保证初始视点的采样均匀.如果是立方体包围盒，则直接以包围盒的8个顶点作为初始视点.

2)记N个视点集合为vp，依次计算vp中N个视点的信息量.假设v(0)best和v(0)worst分别为N个视点中的最佳视点和最不利视点，即

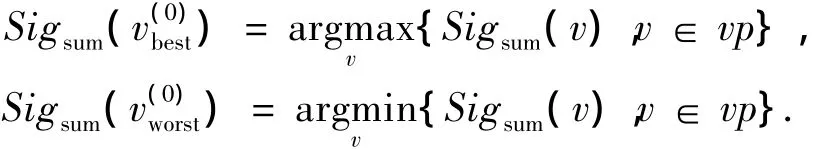
显然，最终的最佳视点和最不利视点都将分别在v(0)best和v(0)worst的周围.设N(v(0)best)和N(v(0)worst)分别为v(0)best和v(0)worst1-邻域，则最佳视点和最不利视点必将落在N(v(0)best)和N(v(0)worst)所围成的区域内或其区域的邻域内.

3)考虑到视点信息量在三维空间中是连续变化的(因为三维空间的连续相关性)，因此，当视点从v(0)best移至最佳视点vpbest和从v(0)worst移至最不利视点vpworst时，视点信息量不会发生突变，而是平滑的过渡.因此，对中的每个三角形进行剖分，剖分规则采用Loop子分模板［13］.

4)记~Nv0为剖分后的新邻域顶点集合，则对中的每个顶点计算视点信息量.以最佳视点为例，如果所有新领域顶点的视点信息量均则将作为新的最佳视点迭代初始值，重复执行步骤3)和步骤4).否则，设作为视点时取得最大视点信息量，则将作为新的最佳视点迭代初始值，类似于步骤2)中关于最佳视点的描述，重复执行步骤3)和步骤4).最不利视点的获取方法类似，不再赘述.图3给出了基于Loop子分模板的最佳视点迭代求精过程.

5)设当前第k次迭代求精时的最佳视点位置为下一次迭代求精后的最佳视点位置为则给定阈值ε，当时，则可以终止最佳视点的迭代过程.最不利视点的情况类似.

3 实验结果及分析

3.1 三维网格模型骨架图

由三维模型顶点相对于其骨架的重要性表示的骨架图提供了非常重要的拓扑知觉信息，图4给出了恐龙和马模型的拓扑知觉骨架图和相应的骨架.其中:图4(a)为原始模型;图4(b)为原始模型相对于线形骨架而言;图4(c)为相应模型的线形骨架，由原始模型顶点的骨架重要性构成的骨架图谱.在图4中阴影部分表示该顶点相对于骨架而言具有较重要的意义，相对于骨架的位移较大，黑色部分则相反.显然，依据拓扑知觉理论关于整体优先的论断来看，不同顶点相对于骨架的位移是空间拓扑知觉在一维的一种表达，这种表达是合理的.本文将在以下试验中进一步从视点选择的角度验证骨架图谱的合理性和准确性.

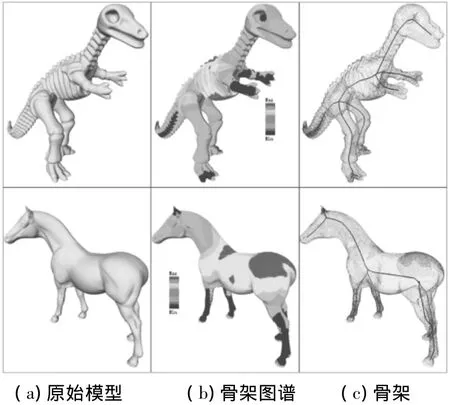
图4 三维模型骨架图及骨架

3.2 三维网格模型最佳与最不利视点选择

为了验证骨架图谱的合理性和准确性，本文实现了基于显著度的视点选择和提出的基于骨架图谱的视点选择.图5描述了从不同视点角度可观测到的视点信息量，该信息量通过视点球线框图进行描述.

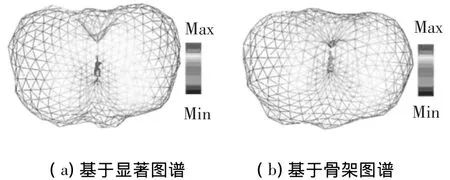
图5 恐龙模型基于显著度和骨架图谱的视点信息量线框图

为了更清晰地比较基于显著图和基于骨架图的视点选择，图6分别给出了3种不同类型的模型在两种特征下的最佳视点的比较.显然，基于骨架图的最佳视点要比基于显著图的更有效，能提供更多的信息.在图6(a)的对比中，基于显著图的最佳视点，由于左前脚对恐龙的腹部的遮挡，使得该视点对恐龙的腹部信息不够丰富.在图6(b)的对比中，两种方式下的最佳视点均提供了较好的视觉信息，图6(c)中两种方式下的最佳视点均选择了人脸的侧面，因为侧面的确能提供最大的信息量，但由于该人脸模型的右嘴唇处有一处疤痕，基于显著图的最佳视点并不能很好地反映这一事实，相反的是，基于骨架图的最佳视点却很好地提供了这个重要信息.因此，最佳视点的选择上，基于骨架图的视点选择相比于基于显著图的方法能提供更多的视觉信息内容，要优于基于显著图的视点选择方法.

在本文中，也实现了最不利视点的选择，图7给出了两种方式下的最不利视点的比较，其中图7(a)，(b)分别为基于显著图和基于骨架图的最不利视点的选择结果.从图7上可以看出，对于恐龙模型和人脸模型而言，两种方法选择的最不利视点均相同，但对于CAD模型，基于骨架图的最不利视点提供的视觉信息明显少于基于显著图的方式，也就是说，根据本文提出的方法得到的最不利视点在视觉内容信息上提供得比基于显著图的更少，即本文的方法能选择更为不利的视点.

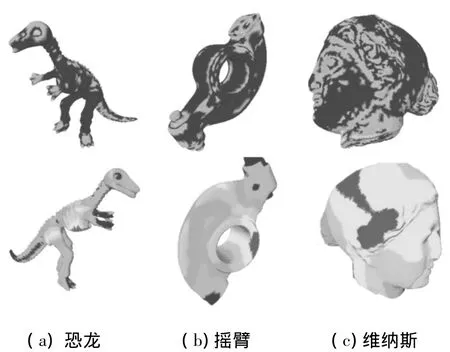
图6 基于显著图和骨架图的最佳视点比较

图7 基于显著图和骨架图的最不利视点比较

3.3 三维网格模型视点快速选择运行时间分析

为了验证和分析本文提出的基于Loop子分模板以迭代求精方式获取最佳视点的运行时间，在本实验中选择了立方体包围盒，即初始视点有8个顶点构成，设定迭代子分终止时的阈值为0.1.算法运行的操作系统为Windows7，处理器为Pentium®双核T4400，2.2 GHz，内存为4 GB.表1给出了本文算法的具体运行时间，从表1中数据可以看出本文提出的基于Loop子分模板迭代求精的视点选择算法运行时间效率高，能快速实现最佳视点或最不利视点的选择.

表1 基于骨架图的视点快速选择方法运行时间分析s

4 结论

1)基于三维模型线形骨架，提出了相对于线形骨架的顶点重要性的定义，并以此定义为三维模型的骨架图谱.

2)基于骨架图谱，定义了视点信息量，并以此作为视点选择的依据.

3)基于Loop子分模板，实现了最佳视点和最不利视点的快速选择，实验结果表明本文的方法要优于基于显著图的视点选择方法.

［1］AU O K C，TAI C L，CHU H K，et al.Skeleton extraction by mesh contraction［J］.ACM Transactions on Graphics，2008，27(3):44.

［2］WADE L，PARENT R E.Automated generation of control skeletons for use in animation［J］.Visual Computer，2002，18(2):97-110.

［3］DEY T K，SUN J.Defining and computing curve-skeletons with medial geodesic function［C］//Proceedings of the Fourth Eurographics Symposium on Geometry Processing.Switzerland:Eurographics Association Aire-la-Ville，2006:143-152.

［4］BIASOTTI S，MARINI S，MORTARA M，et al.3D shape matching through topological structures［J］.Discrete Geometry for Computer Imagery，2003，2886:194-203.

［5］SUNDAR H，SILVER D，GAGVANI N，et al.Skeleton based shape matching and retrieval［C］//Proceedings of the Shape Modeling International.Washington，DC:IEEE Computer Society，2003:130-139.

［6］TAGLIASACCHI A，ZHANG H，COHEN-OR D.Curve skeleton extraction from incomplete point cloud［J］.ACM Transactions on Graphics，2009，28(3):71.

［7］GOOCH B，REINHARD E，MOULDING C，et al.Artistic composition for image creation［C］//Proceedings of the 12th Eurographics Workshop on Rendering Techniques.London UK:Springer-Verlag，2001:83-88.

［8］VÁZQUEZ P P，FEIXAS M，SBERT M，et al.Viewpoint selection using viewpoint entropy［C］//Proceedings of the Vision Modeling and Visualization Conference.［S.l.］:Aka GmbH，2001:273-280.

［9］LEE C H，VARSHNEY A，JACOBS D W.Mesh saliency［J］.ACM Transactions on Graphics，2005，24(3):659-666.

［10］FEIXAS M，SBERT M，GONZÁLEZ F.A unified information-theoretic framework for viewpoint selection and mesh saliency［J］.ACM Transactions on Applied Perception，2009，6(1):1.

［11］NAVON D.Forest before trees:the procedence of global features in visual perception［J］.Cognitive Psychology，1977，9(3):353-383.

［12］CAO J，TAGLIASACCHI A，OLSON M，et al.Point cloud skeletons via laplacian-based contraction［C］//Proceedings of Shape Modeling International.Washington，DC:IEEE Computer Society，2010:187-197.

［13］LOOP C T.Smooth subdivision surface based on triangle［D］.Salt Lake City:University of Utah，1987.