奇异摄动法在复合控制系统设计中的应用

齐乃明，李运迁，阳 勇，高九州

(哈尔滨工业大学航天工程系，15001哈尔滨)

为实现对战术弹道导弹、高速智能巡航导弹、无人驾驶飞行器等的有效拦截，新一代拦截弹多采用气动力与喷流反作用力(RCS)的复合执行机构，以提高控制系统的响应速度和操作性能.RCS包括两种结构:过载型和力矩型.前者位于质心附近，直接产生拦截弹机动所需的过载;后者位于质心的前方(或后方)，用于产生过载和力矩.相对于过载型RCS，力矩型RCS的直接作用是产生使弹体旋转的力矩，改变弹体的姿态，进而产生导弹的机动过载，从这种意义上讲它的工作原理与气动舵是一样的，因此引起弹体旋转的动力学耦合，故控制系统属于多输入多输出系统［1］，设计复杂.

力矩型RCS与气动力复合控制系统的设计难度主要体现在以下3个方面:一是气动力与直接力之间的指令分配;二是气动力属于连续系统，而直接力则具有明显的离散特性;三是直接力的侧向喷流与导弹的外流之间存在很强的干扰，引起参数摄动及模型的不确定性.目前关于第1个方面的研究最多，文献［2］利用模糊理论实现了控制指令在复合执行机构之间的自适应分配;文献［3］则利用最优控制理论，在虚拟力与力矩的帮助下实现了指令的最优配置.文献［4］和［5］的研究主要针对第2个方面，即在考虑连续与离散的特性情况下，对混合控制系统进行了设计.文献［6］则在考虑喷流干扰引起的参数摄动和模型不确定性的情况下，利用高阶滑模理论设计了控制系统.

本文以大气层内低层具有力矩型直接力和气动力的复合控制拦截弹为研究对象，设计末制导段的自动驾驶仪，重点解决控制指令在两个执行机构之间的分配问题.根据气动力与直接力在时间尺度上的差异，利用奇异摄动法将系统分为快、慢两个环节.根据滑模理论与高增益反馈系统及奇异摄动系统之间的联系［8-10］，快变模等价于滑模控制系统中的不确定控制项，用于使系统快速趋向于滑动模态.因此可以设计用于控制RCS的开关面和用于控制气动尾舵的线性反馈控制律.这样既实现了控制指令在两套执行机构之间的分配，也有利于连续系统与离散系统的执行，且便于实际工程实现.而控制系统的时域性能以及鲁棒性，则可以通过最优调节器(LQR)以及Raytheon(雷神)的四环控制机构来实现.

1 奇异摄动法

1.1 快、慢环节

奇异摄动法的解是双重时间尺度法的一种近似解，其核心为:在不同的时间尺度上进行系统分析，从而避免由于奇异摄动所引起的不连续性［8］.

设可用下式表示一奇异摄动线性时不变系统:

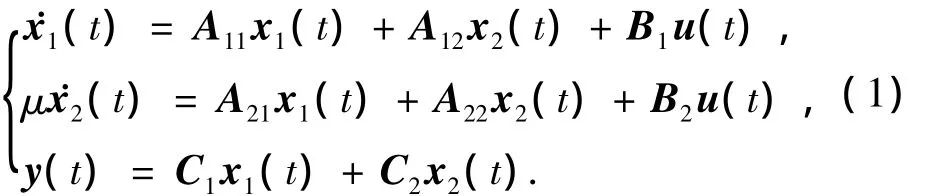
式中:x1为n1维慢变状态变量;x2为n2维快变状态变量(n1+n2=n);u(t)为输入向量;y(t)为输出向量;μ为一小参量.

根据奇异摄动法的基本假设:在快变量的暂态过程中慢变量保持常值，而在慢变量的变化比较明显时，快变量的暂态过程已经结束并达到了它的准稳态.设矩阵A22为非奇异矩阵，即A-122存在，且变量x2是渐进稳定的.当μ→0时，系统(1)退化为

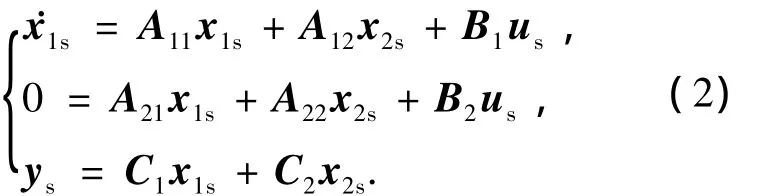
其中下标s表示慢变模.因此，可得

式中x2s为快变量x2的准稳态值.将公式(3)带入公式(2)得

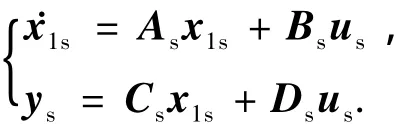
其中:

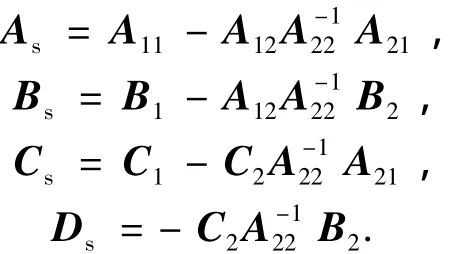
由公式(1)、(2)得

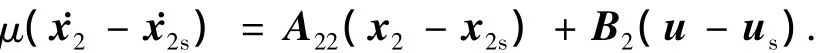
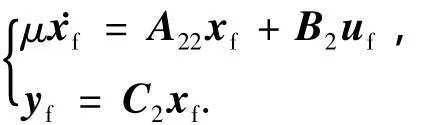
这样原系统变为两个低阶系统，分别设计控制律，最终的控制为u=us+uf.

1.2 奇异摄动与滑模控制的联系

滑模控制一般由两部分组成:一部分为等价控制，系统位于滑模面时保证系统的性能;一部分为不确定控制项，使系统快速趋近滑模面.前一部分属于慢变部分，后一部分属于快变部分.根据文献［7］和［9］的说明，高增益反馈系统与奇异摄动系统之间存在近似关系，而滑模控制也属于一种高增益反馈系统，因此可用奇异摄动法来近似解.且文献［9］已证明慢变模相当于沿滑模的运动，而快变模则可以近似为在滑模邻域内趋向于滑模的运动.

在设计导弹自动驾驶仪时，执行机构的动力学环节往往可近似为一阶惯性环节(A21=0)，在仅考虑一套执行机构，且利用LQR问题来保证系统的时域性能的情况下，系统(1)可分解为［10］

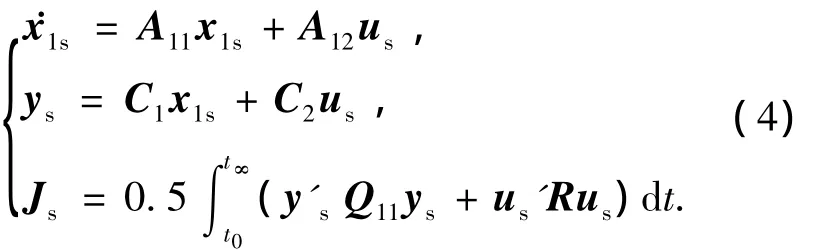
和

通过求解慢变模部分(4)，可得到符合性能要求的滑模σ(x1，x2)=0及等价控制.而快变模的控制指令可近似为［9］

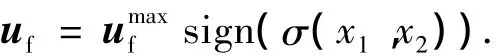
将慢变模的控制指令与快变模的控制指令相加就得到了系统的控制指令.对于复合控制系统，情况较复杂，将在下面介绍.

2 复合控制系统模型

大气层内气动力/直接力复合控制拦截弹的结构如图1所示.RCS位于导弹质心的前方用于产生力和力矩.由于结构、尺寸、质量等的限制，大气层内拦截弹RCS的燃料受到很大的限制，主要在3个阶段使用:一是在发射初期，用于快速转弯;二是在中、末制导的交接班，用于快速捕获目标;三是在末制导的末段用于快速响应制导指令.本文主要针对最后一种情况，也就是末制导末段快速响应制导指令.

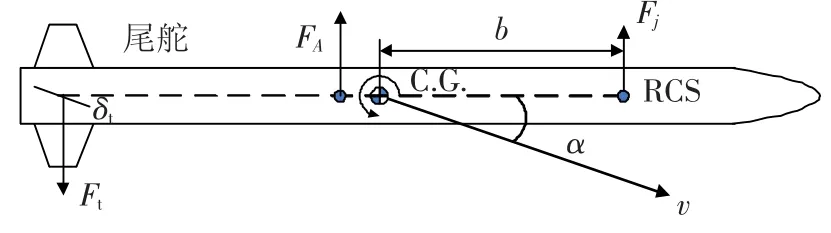
图1 拦截弹结构

拦截弹纵向平面的控制系统短周期模型为

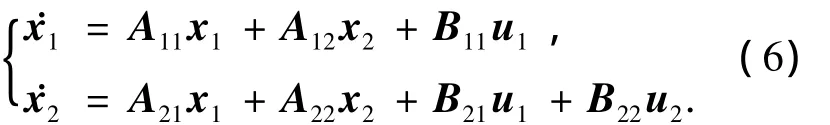
其中:

其中:α为攻角;q为俯仰角速率;δt分别为尾舵的转角和控制指令;δj为RCS的实际值及控制指令;τt、τj分别为尾舵与RCS的等效时间常数.对于大多数的拦截弹，RCS由火箭发动机提供，因此只有0和1两种状态，但在设计时可以先将其设为连续变量，实际使用时采用脉冲调制(PWM)或采样保持(S＆H)的方法［6］，将连续量转化为离散控制指令.参数Zδj与Mδj的表达式为

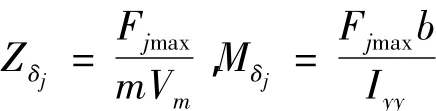
其中Fjmax为RCS的最大推力，δj的取值在-1到1之间.

导弹一般容易测量的信息为导弹过载和俯仰角速率，因此选择这两个量作为输出:

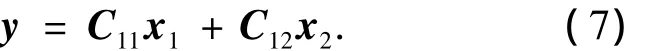
其中y=［Amq］T.

采用奇异摄动法将系统(6)～(7)分解，可得慢变模

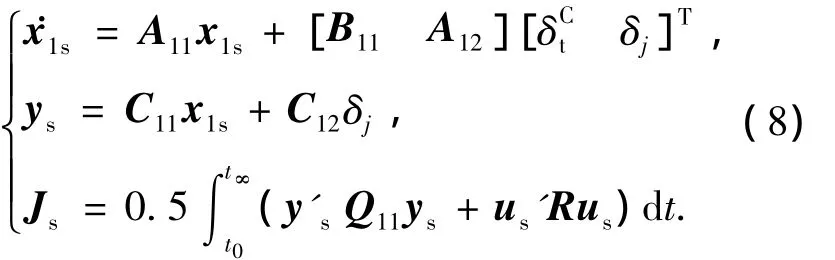
和快变模

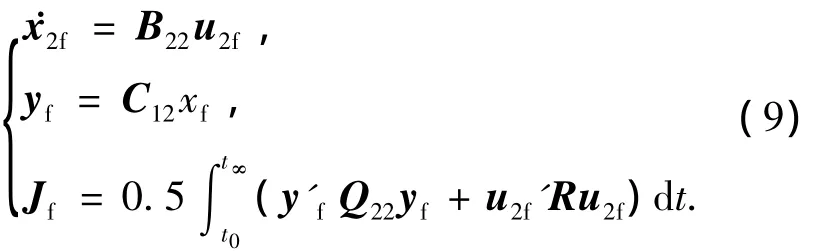
根据第一部分的分析，设计的重点在慢变模部分，通过慢环节最优跟踪器的设计可以得到气动尾舵的线性控制律和RCS的开关面

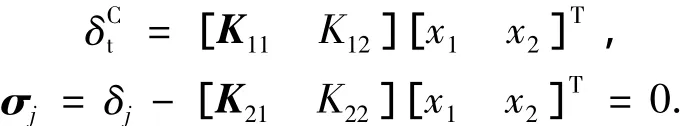
3 控制系统设计

本节主要针对式(8)所示的慢变模部分设计控制系统.

3.1 最优控制器设计

在实际控制中，执行机构的转速同样应该考虑，因此选择性能指标方程如下所示:

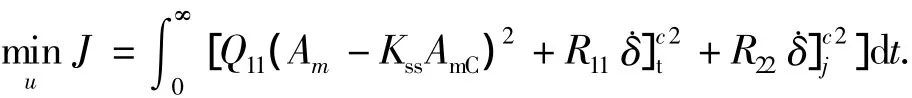
其中AmC为加速度指令，Kss是为了保证稳态误差为零.因此，重构系统为

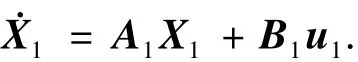
其中

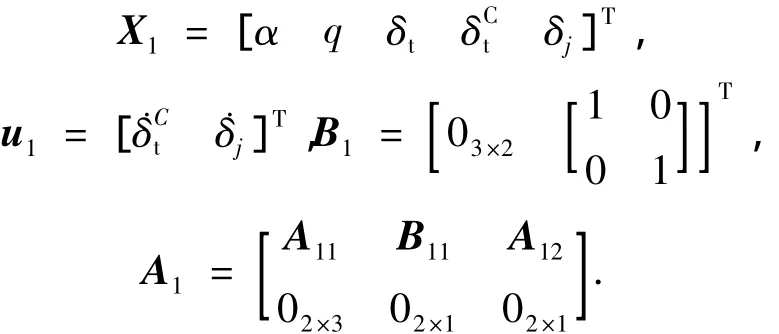
Raytheon的四环控制结构(图2)经过实践的检验具有很好的鲁棒性［11］，因此用来进行控制系统设计.

图2 Raytheon四环控制结构

此外，为实现全状态反馈需要构造5个输出:

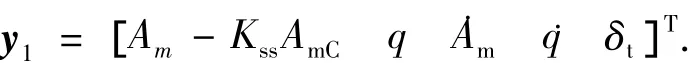
其中

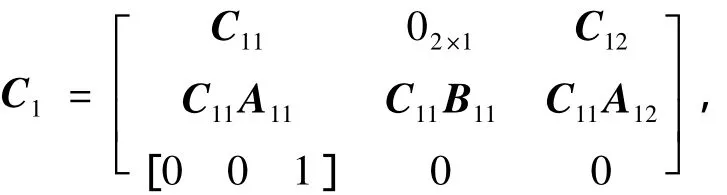
因此，该LQR问题可以写为

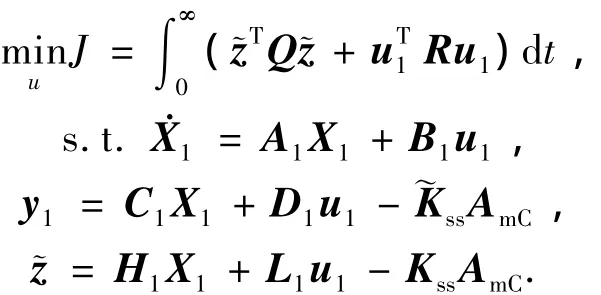
其中

求解代数Riccati方程

其中

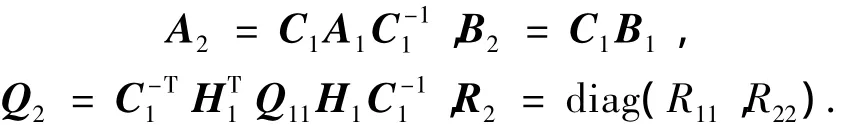
可求得线性反馈控制律

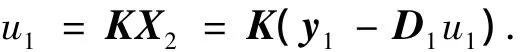
故有

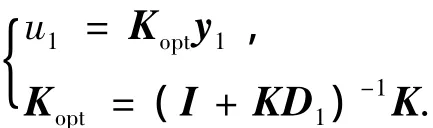
即

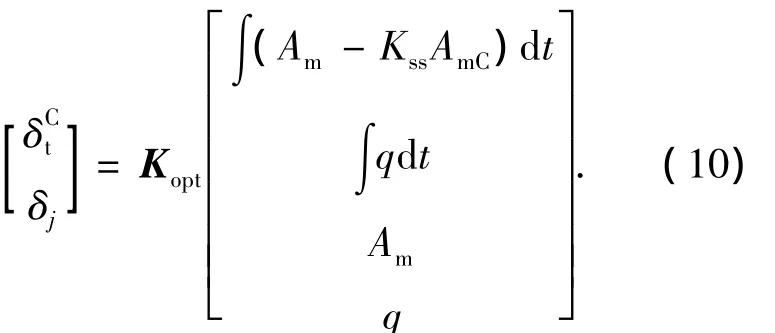
此处需要说明的是，相对于y1上式少了一项，这是因为系统中存在1个不被探测到的极点，为了消除此极点的影响，可以采用文献［12］的方法，即利用稳态的俯仰角速率

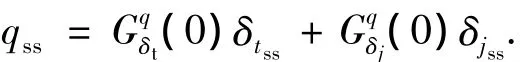
其中Gba(0)为a到b的传递函数的稳态值.具体计算方法参考文献［12］，此处不再详细讨论.此时控制公式(10)变为

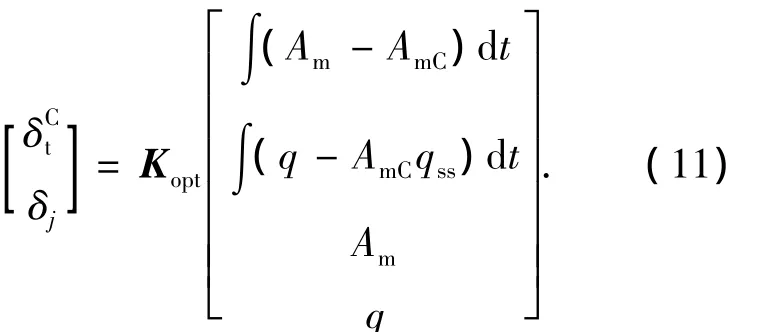
实际自动驾驶仪结构如图3所示，它具有古典控制的结构，易于实际工程实现.

图3 自动驾驶仪结构

3.2 RCS指令

由公式(11)所得到的反馈控制律可直接用于气动尾舵的控制，对于可变推力的RCS，式(11)所得的控制律也可直接用于控制，而对于推力不可调的RCS，它还是难以应用.这时需要构造开关面:

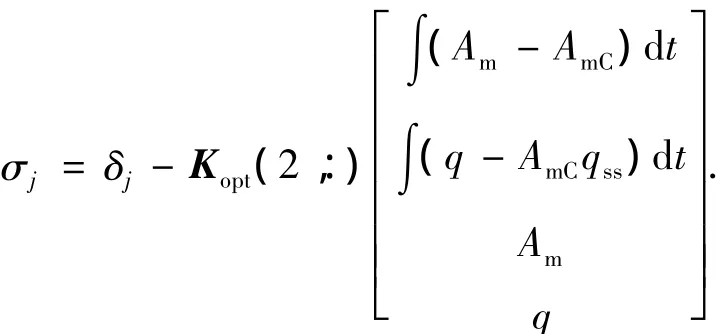
则RCS控制指令可近似为

将σj作为滑模面，利用滑模控制理论也可进行其它设计，此处不再讨论.

4 仿真研究

本部分通过仿真、比较，以检验本文提出的复合控制系统设计方法的性能.仿真参数来自文献［7］.

4.1 RCS推力可调

RCS推力可调的假设虽然与现实不太相符，但是它可以更好的反映系统的一些特性，因此这里首先对RCS推力可调的情况进行了研究.

利用式(11)的控制指令，系统对5g阶跃加速度的响应如图4所示，图中同时给出了仅采用气动尾舵和仅采用RCS时，系统的响应过程.复合控制系统中气动舵和RCS的控制指令如图5所示.

由图4可以看出各执行机构的特点，尾舵响应较慢，具有明显的非最小相位特性，这对于拦截弹的制导精度具有严重的影响，特别是在制导的末段;RCS虽然响应迅速，但是难以稳定;而复合控制系统则是集中了两个执行机构的优点.与文献［7］的结果进行比较，可以看出本文设计的复合控制系统不但响应迅速、容易稳定，而且消除了系统的非最小相位特性，有利于保证高的制导精度.

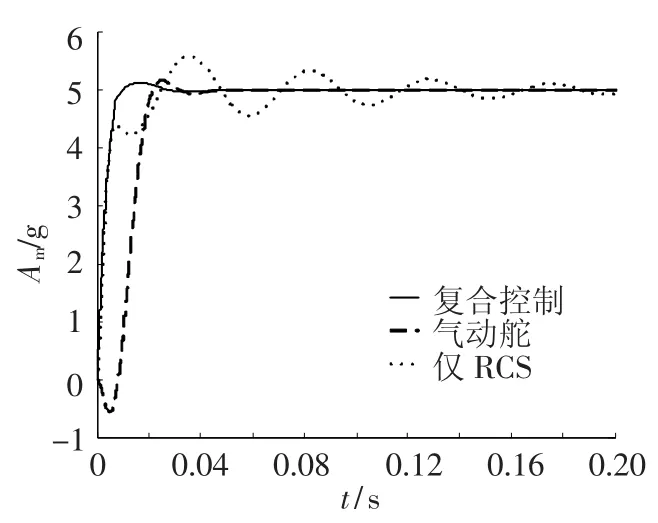
图4 加速度随时间的响应

图5中两个执行机构的转角可以更好的说明这一问题.RCS初始值较大，用于快速响应制导指令，这就是图4中复合控制与仅采用RCS的响应曲线在初始段接近重合的原因，而当系统接近稳定时，RCS的值也趋近于零，这也符合拦截弹RCS燃料受限应尽量节省的规则.尾舵的初始值与RCS的方向相同，主要用于提供系统的阻尼，而当系统稳定时则主要用于提供弹体稳定所需的力矩.由此也说明:复合控制系统的最优指令分配并不是各个执行机构指令最优的简单叠加，而本文设计的复合控制系统可以实现控制指令在执行机构之间的最优配置，而且可以充分发挥它们各自的特点.

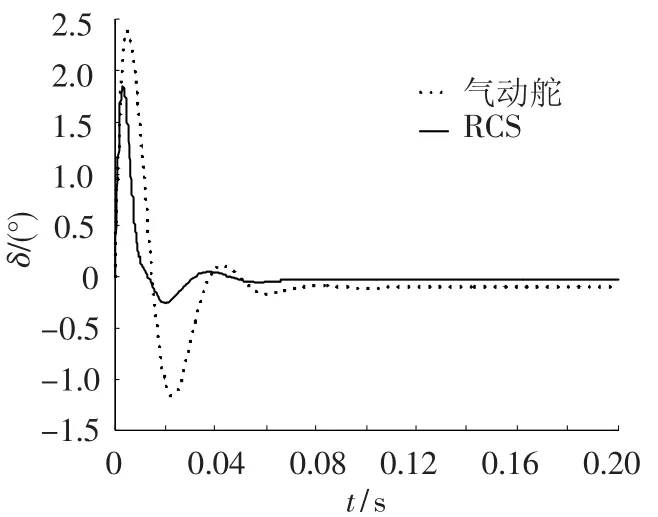
图5 复合控制系统执行机构转角随时间的变化

4.2 RCS推力不可调

当RCS推力不可调时，利用式(12)作为RCS的开关面，所得到的σ值及RCS控制指令分别如图6和7所示.加速度随时间的响应曲线与图4所示近似，只是因为RCS控制指令快速变化而增加了一些抖振，此处不再给出.

RCS的初始值为1，用于快速响应控制指令，这与图4的指令特点是相符的，而当系统趋向于稳定时，在正负之间发生频繁变换.产生这种现象的原因一方面与滑模控制理论的特点有关，一方面也是因为δj的缘故.由图5可以看出虽然δj最终趋近于零，但是并不为零，因此RCS仍要输出一定的指令，而RCS的推力不可调，故造成滑模面σ在正负之间频繁变换.要使RCS的最终指令为零，可以从LQR控制系统的设计入手，在设计过程中加入RCS的稳态值以及最大值的限制，也可以借助虚拟力与力矩的概念进行设计，这将留在以后讨论.此外，对于具有开关推力特性的RCS，可以借助脉冲调频调宽技术将连续信号转化为离散脉冲，便于实际执行机构执行.

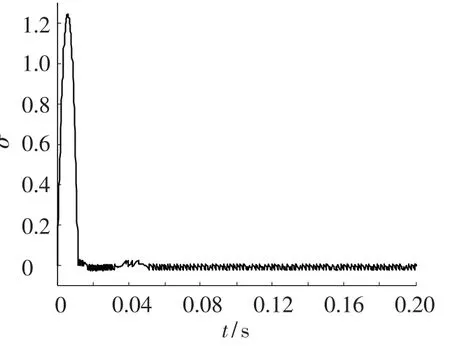
图6 σ随时间的变化

图7 RCS控制指令

5 结论

本文根据直接力/气动力复合执行机构在时间尺度上的差别，采用奇异摄动法将控制系统分为快、慢两个环节.利用Raytheon的四环控制结构和线性最优调节器设计了慢环节的控制律，得到气动舵的线性控制律，并根据奇异摄动法与滑模控制理论之间的关系得到了RCS的线性开关面.仿真结果表明，本文设计的控制系统能够有效地实现控制指令在复合控制机构之间的分配，充分发挥各执行机构的特点，不但提高了系统响应速度，消除了最小相位特性，而且保证了系统的稳定性，有利于实际工程实现.

［1］HIROKAWA R，SATO K.Autopilot design for a missile withreaction-jetusingcoefficientdiagrammethod［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Reston，VA:AIAA，2001:AIAA-2001-4162.

［2］DOMAN D B，GAMBLE B J，NGO A D.Control allocation of reaction control jets and aerodynamic surfaces for entry vehicles［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Reston，VA:AIAA，2007:AIAA-2007-6778.

［3］RIDGELY D B，LEE Y，FANCIULLO T.Dual aero/propulsive missile control-optimal control and control allocation［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Reston，VA:AIAA，2006:AIAA-2006-6570.

［4］尹永鑫，杨明，王子才.直接力与气动力复合控制拦截弹建模与控制［J］.航天控制，2006，24(4):18-22.

［5］周荻，邵春涛.大气层内拦截弹直接侧向力/气动力混合控制系统设计［J］.宇航学报，2007，28(5):1205-1209.

［6］TURNES C，SHTESSEL Y，SHKOLNIKOV I.Missile controlled by lift and divert thrusters using nonlinear dynamic sliding manifolds［J］.Journal of Guidance，Control，and Dynamics，2006，29(3):617-625.

［7］WEIL R D，WISE K A.Blended aero＆reaction jet missile autopilot design using VSS techniques［C］//Proceedings of the 30th IEEE Conference on Decision and Control.Piscataway:IEEE，1991:2828-2829.

［8］戴师正.奇异摄动理论［J］.系统工程与电子技术，1988，2:1-12.

［9］YOUNG K D，KOKOTOVIC P V，UTKIN V I.A singular perturbation analysis of high-gain feedback systems［J］.IEEE Trans on Automatic Control，1977，AC-22(6):931-937.

［10］CHOW J H，KOKOTOVIC P V.A decomposition of near-optimum regulators for systems with slow and fast modes［J］.IEEE Trans on Automatic Control，1976，AC-21:701-705.

［11］MRACEK C P，RIDGELY D B.Missile longitudinal autopilots:connections between optimal control and classical topologies［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Reston，VA:AIAA，2005:AIAA 2005-6381.

［12］MRACEK C P，RIDGELY D.B.Optimal control solution for dual(tail and canard)controlled missile［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Reston，VA:AIAA，2006:AIAA-2006-6569.