神经网络补偿的挠性卫星敏捷姿态机动

耿云海，吴炜平，2，马玉海

(1.哈尔滨工业大学卫星技术研究所，150001哈尔滨;2.中国运载火箭技术研究院研发中心，100076北京)

大多数的挠性敏捷卫星，既要求具有快速大角度姿态机动能力，又涉及到高精度成像时的稳定控制问题.对于快速大角度机动卫星来说，多采用控制力矩陀螺(CMG)作为执行机构.Wie B［1-2］对控制力矩陀螺的操纵律和构型进行了大量的研究，并针对单轴机动要求高的卫星提出双SGCMG的平面构型.控制力矩陀螺提供的输出力矩大，但是控制力矩陀螺具有过零摩擦特性，它所能提供的最小输出力矩很难满足高精度指向控制的要求.本文针对此类卫星的特征，设计混合执行机构系统.

姿态快速机动时容易激起挠性附件振动，在轨运行也会受到各种外加干扰的作用，因此要求卫星控制系统应具有较强的鲁棒性.变结构控制具有克服模型不确定性、未建模动态特性以及输入非线性等问题的特性.国内外学者将变结构理论应用到航天器姿态机动等方面进行了大量的研究［3-5］，许多文献中将挠性附件弹性振动考虑为卫星控制系统输入干扰项或者控制系统模型不确定项，不能反应挠性卫星系统多变量强耦合的特征.在离散和时滞系统，加入积分项的变结构控制可以有效的补偿系统本身带来的控制量输出量的相位差，在复杂挠性卫星系统中同样存在着类似的问题，而且还体现出多变量强耦合的特性.

文献［6］采用模态观测器，设计渐近稳定的抑制算法，文中只是针对惯量不变航天器，对具有参数不确定性系统很难推广.对于方程中含有不确定项的系统，常采用自适应等逼近方法对该项进行估算.文献［7］中采用自适应逼近方法估算参数时需要大量的测量数据.而神经网络可以避免这一问题，并且通过不断的将新数据融入参数估算结果中，参数估计结果会不断地被修正.可以选取径向基函数网络对系统需要进行参数估计的项进行处理，从而降低控制系统的设计要求，提高执行机构效率.具有不确定参数的系统逼近问题已在稳定控制中有应用研究［8-9］，但具有弹性振动的大角度快速机动问题尚没有涉及到.

本文研究以上述提出的混合执行机构作为动装置的卫星姿态快速机动问题，同时考虑卫星惯量不确定性、挠性附件振动及外部干扰作用.设计具有自适应逼近的变结构控制算法，该控制方法采用积分型滑模面，利用径向基神经网络估计由卫星转动惯量不确定性和挠性振动引起的函数项，并在控制律设计中对其进行补偿，消除不确定项对系统的影响，提高卫星姿态控制性能.最后通过卫星仿真算例，验证上述方案的有效性.

1 数学模型

1.1 挠性卫星的动力学方程

方程可通过计算Lagrange函数L=T-U推出［10］，表示为

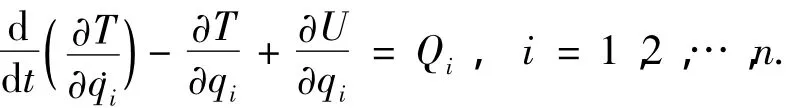
其中qi为广义坐标，Qi为与之对应的广义力.

动力学方程可整理为

其中:J为挠性卫星本体惯量矩阵;ω为星本体相对惯性空间的角速度;Fs为卫星本体相对于挠性附件的运动耦合矩阵;η为挠性附件的弹性振动模态;Λ为弹性振动频率矩阵;ζ为弹性振动阻尼矩阵;Hb为星本体角动量;h为卫星内飞轮及控制力矩陀螺等转动部件的角动量;Td为各种摄动引起的干扰力矩;Tc为控制力矩.

对动力学方程式(1)进行小量化处理后，可得到混合坐标方程形式为

其中θ为三轴姿态角.

卫星姿态机动过程中，期望姿态欧拉角为θd，期望角速度为测量系统得到的量测量中姿态欧拉角为θ，角速度为为了得到误差系统状态量，令e=θ-θd,

取系统变量为x=［］T，则误差系统的状态方程可以表示为

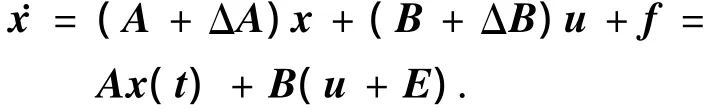
假设在系统中ΔA、ΔB及干扰项f有界，且为匹配不确定项，系统的模型不确定项E可表示为E=B+(ΔAx+ΔBu+f)，B+=(BTB)-1BT.

挠性附件模态可以通过设计观测器得到［5］，设计扩展变量ψ=η+δω，将其代入式(1)，即可得到如下形式的模态坐标系统:

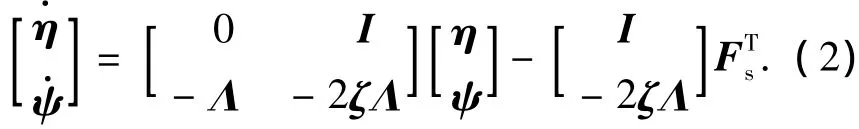
对于式(2)设计龙贝格观测器，采用极点法保证系统响应及动态特性.进一步降低观测器维数，采用估计部分模态的方法，可以充分利用量测信息.

1.2 控制力矩陀螺模型

大部分敏捷卫星，特别是对地定向卫星对偏航轴的机动能力要求不强，而俯仰、滚转轴则需要频繁、快速、大角度机动.所以在指向地心的偏航轴可以利用反作用飞轮进行姿态控制，在俯仰轴和滚转轴构成的平面内，需要提供1个面内的力矩，采用两个平行构型的单框架控制力矩陀螺，如图1所示.

图1 双平行陀螺群角动量

在体坐标系的Oxbyb平面内，陀螺群的角动量h可表示为

其中:h0为转子角动量;框架角δ=［δ1δ2］T;A为雅可比矩阵，如下:

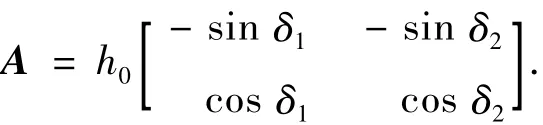
可以得到满足力矩方程和优化指标Jmin=0.5δTδ的伪逆解

对于双平行构型的单框架控制力矩陀螺来说，当δ=［0π］T时，雅可比矩阵为

此时存在奇异向量u=［10］T，使得ATu=0.同时δ=±［0π］T之外，δ=±［π/2-π/2］T也是奇异点.采用文献［6］中奇点规避的操纵律，由力矩方程δ=A#h，其中:

A#=WAT［AWAT+V］-1.操纵律中，

其中κ=0.1cost，λ=0.01exp［-10det(AAT)］.

2 执行机构配置

对于大角度机动的卫星，陀螺群系统很容易遇到奇点.而对于卫星本体系Oxbyb平面内的双SGCMG平行构型(如图2所示)，要保证该构型能够提供该平面内任意方向的力矩，必须保证陀螺群角动量和方向与姿态机动方向夹角不为零，最好始终保持90°夹角以便最大限度提供机动力矩.可以在大角度机动前调整双平行构型，使两个SGCMG保持平行并绕各自框架轴转动到非奇异位置.这样不会引起附加力矩也能保证足够大的机动能力.

图2 混合执行机构

对于星体Ozb轴可采用飞轮，构成1飞轮+2平行布置单框架力矩陀螺的基本执行机构配置.由于力矩陀螺框架角速度较小时，提供力矩误差较大，与飞轮相比，姿态控制精度较低.也可采用2平行布置单框架力矩陀螺+3反作用飞轮，以提高系统冗余度，提高控制精度.在姿态敏捷机动时选用力矩陀螺提供较大力矩、缩短姿态调整时间，而在机动末端转为反作用飞轮控制，以缩短过渡过程，提高姿态指向精度.此时，控制量Tc为

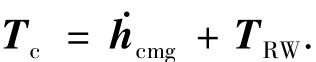
3 控制器设计

3.1 变结构控制器设计

针对模型不确定性问题，采用积分型滑模面［11-12］

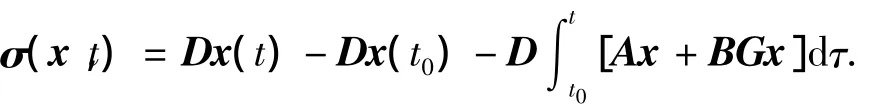
其中-Dx(t0)项可保证σ(x(t0)，t0)=0时的相平面轨迹能够到达原点;G可通过极点配置选取.选

其中K=-(DB)-1DA，非线性项中增益ρ满足条件‖ρ‖＞‖E‖.

选取V=0.5σTσ为Lyapunov函数对控制器进行稳定性分析

当系统存在参数项无法精确得到，只能取最大边界进行计算时，最终的控制量冗余度较大，即导致参数ρ的选取保守，导致执行机构负载要求过高，误差较大.故针对参数项无法精确得到的问题，采用设计补偿器方法予以解决.

3.2 神经网络补偿器设计

对于挠性卫星模型式(1)，尽管已考虑弹性振动模态，但控制器设计中，存在模态截止误差及其他未建模误差导致控制器参数与实际模型不符，而且无法估算模型不确定项E的上界.故设计如图3所示的补偿器系统.将设计的神经网络加入姿态控制系统中，在每个控制周期里，通过神经网络补偿器对每个周期的E项进行估算，并且控制律设计中考虑不确定项E引起的偏差.采用RBF神经网络对增益ρ

图3 姿态控制系统

描述为

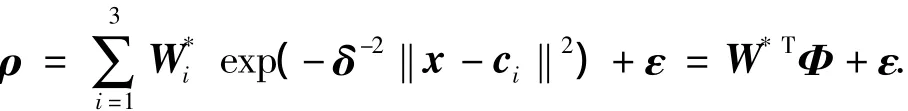
式中:Φ为高斯基函数;ci为基函数的最优中心向量;x为基函数输入向量;W*T是最优加权系数;ε为估算误差.

神经网络的权重调整律为

式中γi＞0为参数学习速率;σi为切换函数的第i列，有σ=［σ1σ2σ3］.

设*-W，取稳定性函数

在设计神经网络时，基函数层的函数个数并非越多越好，以满足所估算的系统阶数为标准，需要考虑计算量及时间等因素.实际应用中可采用先验信息选取中心向量等参数，以提高估算精度.

4 仿真算例

挠性卫星转动惯量矩阵和耦合矩阵为

振动频率矩阵:

阻尼矩阵:

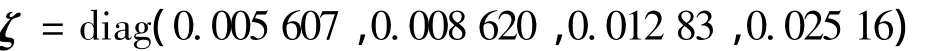
混合执行机构配置采用2平行构型单框架力矩陀螺+1反作用飞轮，力矩陀螺标准角动量15 N·m·s，最小框架角速率±0.02(°/s)，最大输出力矩3.5 N·m;反作用飞轮最大输出力矩±0.25 N·m.

卫星所受的空间环境的干扰力矩模型为

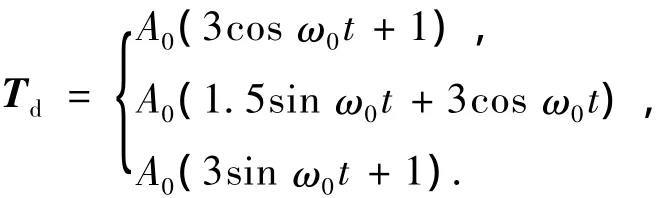
其中干扰力矩幅值A0=1.5×10-5N·m，轨道角速度ω0=-0.001 1(rad/s).控制器参数

神经网络补偿器输入量共9个，为姿态欧拉角、姿态角速度测量值和控制律中的Kx项;加权系数初始值为Wjk=0(k=1，2，3);参数学习速率0.01;隐含层选取6个神经元，网络中第j个神经元中心为cji=1×random-0.5(i=1，2…，6;j=1，2，…，9).

挠性卫星控制力矩陀螺框架角初始位置δ=［π/45π/4］T，初始姿态角θ=［0 0 0］T，初始姿态角速率θ=［0 0 0］T.卫星从t=0开始，俯仰轴进行60°姿态机动，然后稳定在目标姿态.

考虑无补偿器和有补偿器两种情况说明本文方法的可行性.挠性卫星在敏捷机动时，引起挠性附件的弹性振动，造成系统模型参数变化无法精确估算，假设转动惯量变化量为20%.仅采用变结构反馈进行控制，其中参数ρ采用经验估计值.仿真结果如图4～5所示.航天器在50 s内姿态指向变化60°，从图4可得卫星指向稳态误差在50 s达到0.1°，卫星在50 s姿态稳定度达到0.1(°/s);从图6可以看出存在补偿时，姿态指向精度明显提高.

采用补偿器对不确定项进行估算.结果如图6～9.图6与图4相比较，卫星机动末端过渡过程缩短10 s，角速度偏差更小，图6中卫星指向精度在40 s达到0.1°，姿态稳定度达到0.02(°/s)，一般情况由于弹性振动阻尼较小、衰减时间长，而本文设计的补偿器通过反馈形式，相当于人为增加系统阻尼，有效地削弱了弹性振动对系统的影响;从图7可知，双平行构型单框架力矩陀螺在角动量平面内的度量矩阵没有出现奇异.当出现垂直于2框架陀螺平行轴方向的控制量时，该构型可以通过操纵律中添加的偏置量改变平行轴的角度，从而使力矩陀螺的输出力矩方向逃出奇异点.从图8给出的神经网络估计值输出量可看出，神经网络估计值约在30 s达到稳定，估计值的偏差约为0.01 N·m.图9为有补偿器情况下的弹性振动各阶模态响应曲线，对比图5可以看出，神经网络补偿器使各阶模态均得到有效抑制.

图4 无补偿时姿态信息

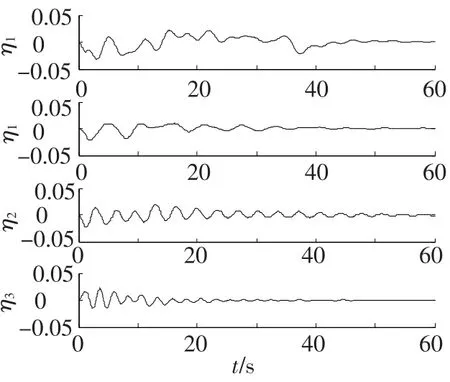
图5 无补偿时附件振动模态坐标

图6 有补偿时误差姿态角信息

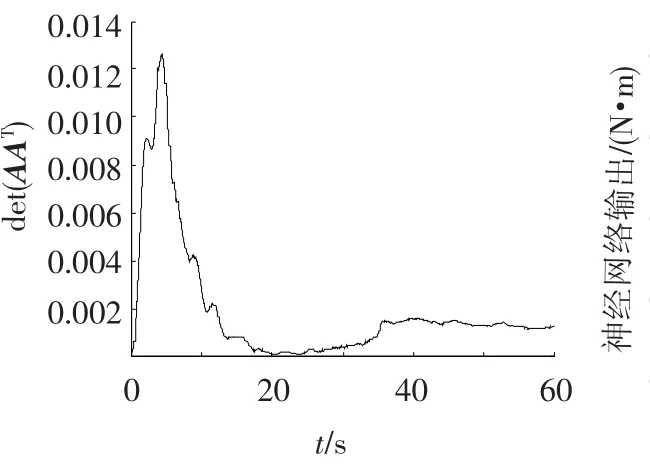
图7 双SGCMG构型奇异度量值变化曲线

图8 不确定项估计值幅值

图9 有补偿时附件振动模态坐标

5 结论

针对快速机动航天器，采用混合执行机构配置，提出了一种自适应逼近的变结构控制方案，扩展状态变量设计观测器，采用神经网络补偿器对振动引起的数学模型参数变化性进行补偿，消除其对系统的影响.所设计的控制器有效地解决了卫星参数不确定、挠性振动影响及环境力矩干扰等对姿态机动过程的影响，加快了收敛速度，提高了过渡过程的动态品质.

［1］WIE B.Singularity escape/avoidance steering logic for control moment gyro systems［J］.Journal of Guidance，Control and Dynamics，2005，28(5):948-956.

［2］LAPPAS V，WIE B.Robust control moment gyroscope steering logic with gimbal angle contraints［J］.Journal of Guidance，Control and Dynamics，2009，32(5):1662-1666.

［3］VADALI S R.Variable-structure control of spacecraft large-angle maneuvers［J］.Journal of Guidance，Control and Dynamics，1986，9(2):235-239.

［4］BOŠKOVIC＇J D，LI S-M，MEHRA R K.Robust stabilization of spacecraft in the presence of control input saturation using sliding mode control［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Reston，VA:AIAA，1999，3:1960-1970.

［5］BOŠKOVIC＇J D.Robust tracking control design for spacecraft under control input saturation［J］.Journal of Guidance，Control，and Dynamics，2004，27(4):627-633.

［6］DI GENNARO S.Output stabilization of flexible spacecraft with active vibration suppression［J］.IEEE Transaction on Aerospace and Electronic Systems，2003，39(3):747-759.

［7］DE RUITER A H J.Effect of attitude parameterization on the performance of passivity-based adaptive attitude control［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Reston，VA:AIAA，2001.

［8］康兴无，陈刚.轨道快速机动期间的姿态鲁棒稳定控制方法研究［J］.宇航学报，2009，30(4):1510-1515.

［9］黄喜元，王青.基于归一化神经网络的航天器自适应姿态跟踪控制［J］.宇航学报，2011，31(11):2542-2549.

［10］耿云海，崔祜涛.挠性飞行器的脉冲调制控制［J］.宇航学报，1997，18(4):37-43.

［11］CAO Wen-jun，XU Jian-xin.Nonlinear integral-type sliding surface for both matched and unmatched uncertain systems［J］.IEEE Transactions on Automatic Control，2004，49(8):1355-1360.

［12］LEE K W.Adaptive control of spacecraft with flexible appendages using nussbaum gain［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Retson，VA:AIAA，2007，AIAA 2007-6326.