自由漂浮柔性空间机器人轨迹跟踪控制

胡庆雷，翟艳霞，霍 星，2

(1.哈尔滨工业大学控制科学与工程系，150001哈尔滨;2.渤海大学工学院，121013辽宁 锦州)

随着空间技术的发展，空间机器人技术得到广泛的应用.质量轻、成本低、大范围的柔性空间机器人成为了现代空间技术的迫切需求［1-5］.在空间机器人操作时，为了节省燃料，通常关闭航天器本体姿态控制器，使其处于自由漂浮状态［6］.然而，柔性空间机器人在运动和操作时会产生扭曲、弹性、剪切等变形，这将影响空间机器人的稳定性和控制精度.同时，由于空间机器人存在刚性与柔性的耦合，使得描述该系统的运动变得很复杂.因此，研究柔性空间机器人的动力学分析及控制十分必要.

许多学者对柔性机器人控制问题做出了研究.采用奇异摄动方法，文献［7］将柔性机器人的系统分离为刚性与柔性两部分，并进而对其动力学控制问题展开深入研究.考虑到存在参数不确定性，文献［8］提出一种增广自适应控制方法来解决空间机器人的控制问题.针对自由漂浮柔性空间机械臂末端跟踪控制问题，Green在文献［9］中提出了一类自适应模糊控制方法，并采用仿真方法验证了所提方法的有效性.此外，文献［10-15］针对刚性空间机器人的轨迹跟踪控制问题也展开了一些相关的研究.然而，尽管在上述的研究成果中针对于刚性机器人给出了可行的控制方案，但是对于柔性空间机器人的控制，目前研究成果相对较少，尤其是考虑柔性振动、欠驱动及存在系统载体姿态干扰的自由漂浮柔性空间机器人轨迹跟踪控制研究比较欠缺.在这方面，文献［14］采用变结构控制方法在自由漂浮柔性空间机器人轨迹跟踪控制方面也展开初步的研究与探讨.

为此，本文在上述研究结果的基础上，对存在载体姿态干扰的自由漂浮柔性空间机器人系统，考虑系统柔性振动及欠驱动问题，提出一种非奇异终端滑模控制方案，以期实现系统关节空间的轨迹跟踪控制.该方案采用自适应控制技术在线学习系统干扰参数;同时加入条件积分改进了终端滑模面，以消除干扰带来的稳态误差.Lyapunov稳定性法分析证明了该控制器能够使轨迹跟踪误差收敛到零.最后，仿真结果表明该方案能够实现对期望轨迹的跟踪.

1 数学模型

设自由漂浮柔性空间机器人系统由自由漂浮的刚性载体B0和柔性机械臂B1、B2组成，如图1所示.系统处于微重力环境中，忽略重力影响;柔性杆为均匀细长杆，忽略轴向变形和剪切变形，视为Euler-Bernoulli梁［6，14］.建立各个分体Bi的连体坐标系Oixiyi，i=0，1，2及惯性坐标系OXY.

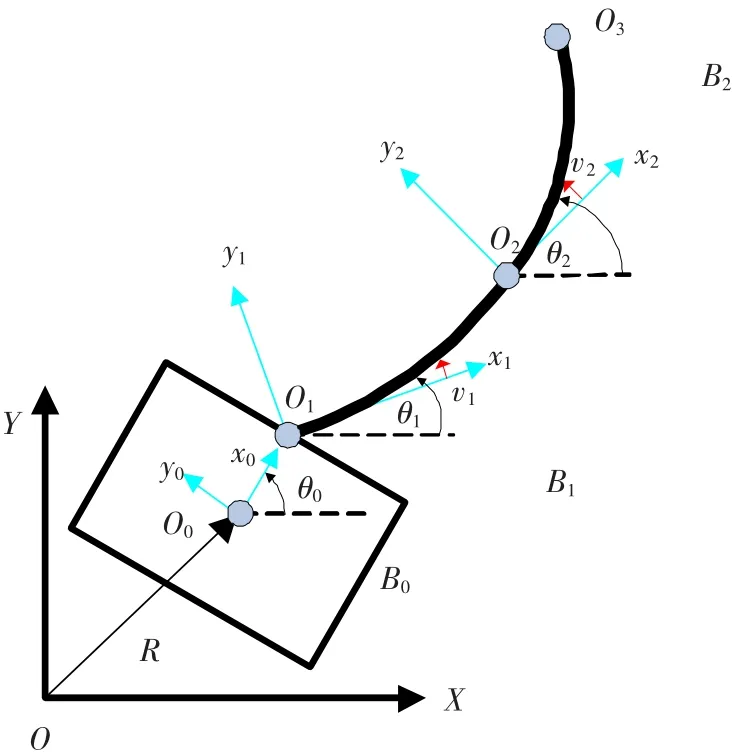
图1 自由漂浮柔性空间机器人的结构模型

根据拉格兰日法与假设模态法，经过推导可以得到的系统动力学方程［7-10，16］:

其中:q=［xsysθ0θ1θ2q1q2］T为系统的广义坐标，xs、ys、θ0为系统载体位置和姿态，θ1、θ2分别为关节1、关节2转角，q1、q2为模态坐标;M(q)为系统质量矩阵;C(q，q)为包含各种摩擦力的参数矩阵;K=diag(0，k1，k2)为刚度矩阵，其中振动模态φ(xi)=sin(π/li)xi

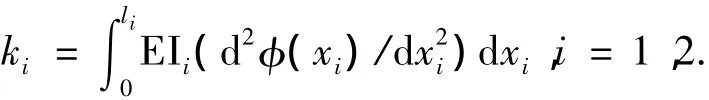
2 动力学分析

自由漂浮柔性空间机器人系统刚性运动与柔性振动相互耦合，同时机械臂操作期间系统载体的位置和姿态是不受控的，方程(1)是高度非线性、非完整约束、欠驱动的.

设集中力

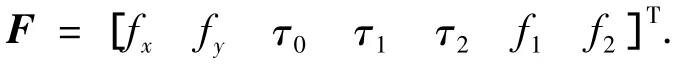
其中fx、fy分别为作用于系统载体水平方向和垂直方向的控制推力;τ0为作用于载体的外部转矩;τ1、τ2为作用于连杆关节转矩;f1、f2为作用于柔性连杆上主动振动控制力.由于系统载体位置、姿态不受控

设q=［qTrqTe］T表示刚形体位移矢量，其中qr=［qTpqTa］T，qp=［xsysθ0］T，qa=［θ1θ2］T;而qe=［q1q2］T为柔性变形位移矢量.根据文献［14］可得

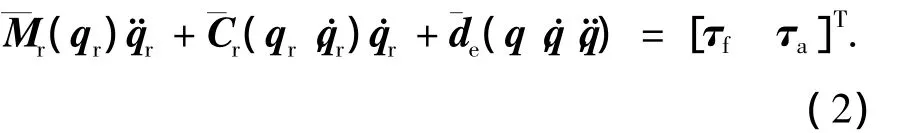
由于Mpp可逆，方程(3)变形代入方程(4)，整理化简可得

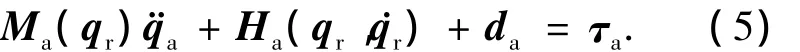
其中:

对于自由漂浮柔性空间机器人系统，方程(5)将柔性振动作为系统扰动的一部分，并且将欠驱动问题转换为全驱动问题.本文将通过方程(5)设计控制算法实现系统轨迹跟踪.

3 控制器设计

在简化动力学模型(5)的基础上，假设期望的轨迹为qad=θd，则其相应的跟踪误差定义为e=qa-qad.由方程(5)可知

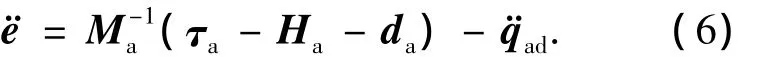
选取如下非线性滑模面［17-23］:

其中β=diag(β1，β2)，并且βi＞0(i=1，2);p和q均为奇数，且0＜q＜p＜2q.

注1 对向量z∈Rn×1，定义

根据等效控制设计方法，控制律形式可描述为

其中τeq为等效控制作用，τsw为切换控制作用.

当系统状态进入滑模面上后，即满足s=0与=0.由此，可以确定等效控制

为确定切换控制作用保证滑动模态的存在，考虑系统扰动项，设系统扰动项d=M-1ada.

假设1系统扰动d(t)有界，且满足下列不等式:

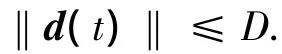
其中D为未知的干扰界.

对于未知常数D的选取，本文给出一种自适应学习的方法［22］来实时在线对其估计.因此，设计如下非线性控制部分:

其中k＞0，D为D的估计.为了避免外部干扰对D影响，给出如下改进型自适应学习律［22］:

式中:γ为自适应因子;μ(t)=-rμ(t)，且r＞0，μ(0)＞0.

定理1考虑系统(6)且满足假设1.如果选取滑模面(7)，并采用给出的控制律(8)以及参数自适应律(9)，则系统在有限时间内到达滑模面s(t)=0，也即系统满足有限时间稳定.

证明考虑如下Lyapunov函数:

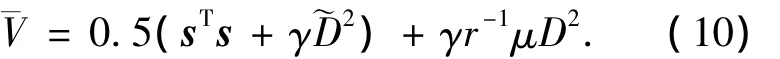
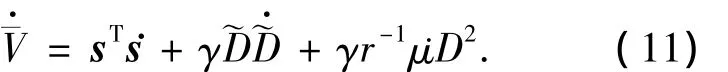
将式(8)、(9)代入式(11)可得

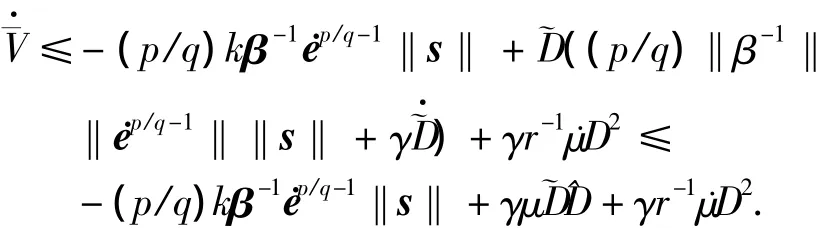
由μ(t)=-rμ(t)可知，

由此，当s(0)≠0时，考虑到p、q为奇数，且1＜p/q＜2，可得p/q-1≥0，也即≤0，系统是有限时间稳定，并且满足s(t)=0.

此外，当s=0满足后，系统(6)可改写为e+，同时可得有限收敛时间ts为［17，21-22］

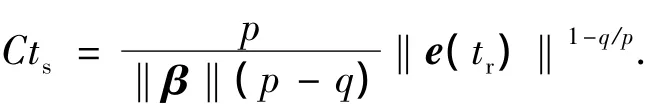
此外，为了减小滑模控制的抖振，采用饱和函数sat(s/φ)来替代符号函数sgn(s)，即

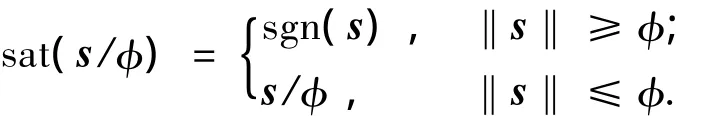
其中φ＞0为边界层厚度［24］.控制律τa=τeq+τsw有

为了避免积分饱和问题［25-28］，给出如下改进的滑模面:

其中α=diag［α1，α2］，αi＞0(i=1，2)，并且参数α、β选取使得多项式s2+β-1is+αi(i=1，2)为Hurwitz多项式;σ满足

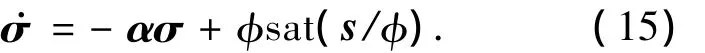
定义增广误差ea≜e+β-1p/q，显然，在边界层外，也即‖s‖≥φ，式(15)可改写为σ=-ασ+φsgn(s);在边界层内，也即‖s‖≤φ，式(15)改写为σ=e+β-1p/q=ea.由此，可有如下结论:

定理2考虑系统(6)，满足假设1并选取滑模面(14).如果采用控制律(13)与参数自适应律(9)，则闭环系统是有界稳定的.

证明基于上面的分析，该证明将分两种情况展开讨论:

2)对s求导，可得

如果选取Lyapunov函数(10)，并对其求导可得

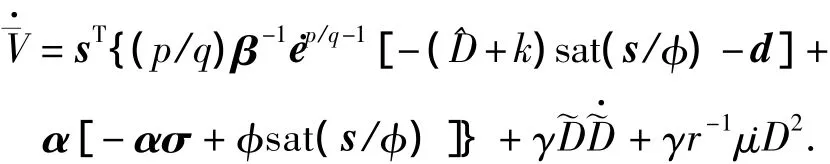
当‖s‖≥φ时，sat(s/φ)=sgn(s);由(1)知‖sat(s/φ)‖≤1，‖σ‖≤φ/‖α‖，可得

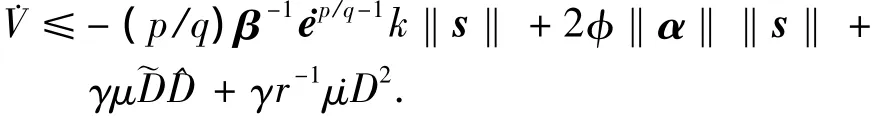
由式(12)，且当s≠0时ep/q-1＞0可知

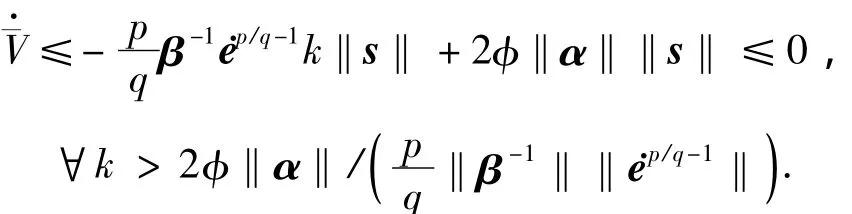
当‖s‖≤φ时，sat(s/φ)=s/φ，=ea=e+β-1p/q;由于积分的存在，当t→∞将使得ea=0，进而e=0.至此定理得证.

4 仿真比较与分析

采用文献［9］给出的柔性空间机器人系统物理参数m0=600 kg，b0=3.0 m，m1=m2=1.507 5 kg，l1=l2=4.5 m和FEI1=FEI2=1 676 N·m2进行仿真验证.假设期望轨迹与初始值分别为

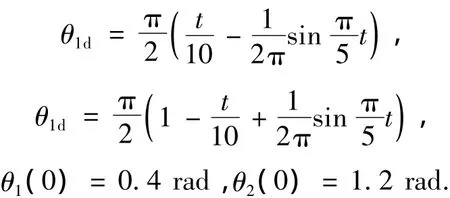
此外，在仿真研究中，假设系统控制力矩输入限制在｜τi｜≤10 N·m，i=1，2，并且相应的控制器参数选取为β=diag(0.5，1)，α=diag(15，18)，q=7，p=9，k=2，φ=0.05;γ=10，r=5和μ(t)=e-5t.

4.1 无载体干扰的仿真结果

在这种情况下，分两种情况:采用滑模面(7)的控制器(8)与采用滑模面(14)的控制器(19)进行仿真，并进一步与传统的PID控制仿真进行比较.仿真结果如图2～5所示.从仿真图中可知，系统在PID控制及本文设计控制器输入力矩在相同限制条件下，均能跟踪期望关节转角;显然本文设计的控制器关节转角误差更小，跟踪精度更高;同时，控制作用只是引起微小的柔性模态振动.

4.2 载体干扰下的仿真结果

在上述相同的控制参数与仿真初始条件下，假设在仿真时间t=30 s处，突然加入载体干扰力矩τf=［0010］T(N·m)，其相应的仿真结果如图6所示.仿真结果表明:在存在载体姿态干扰的情况下，选取滑模面(14)的控制器(19)稳态跟踪误差更小，相对于选取终端滑模(7)的控制器(8)跟踪精度很高.

图2 输入控制转矩

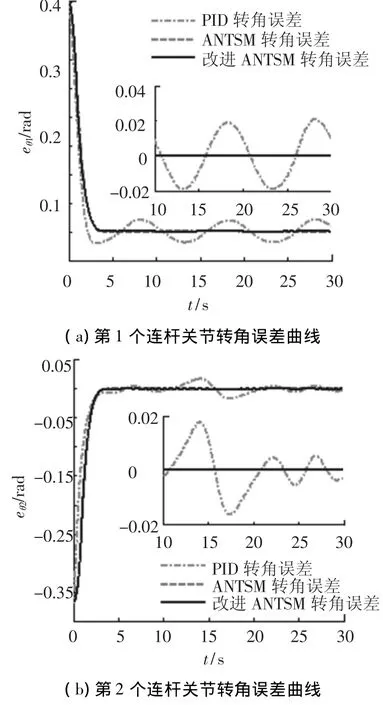
图3 关节转角误差曲线

图4 关节转角曲线

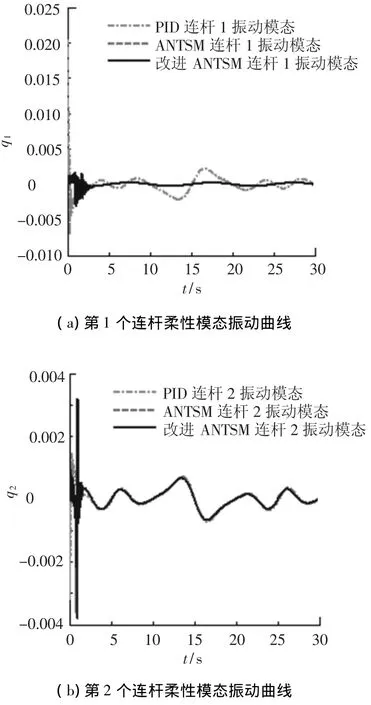
图5 柔性模态振动曲线

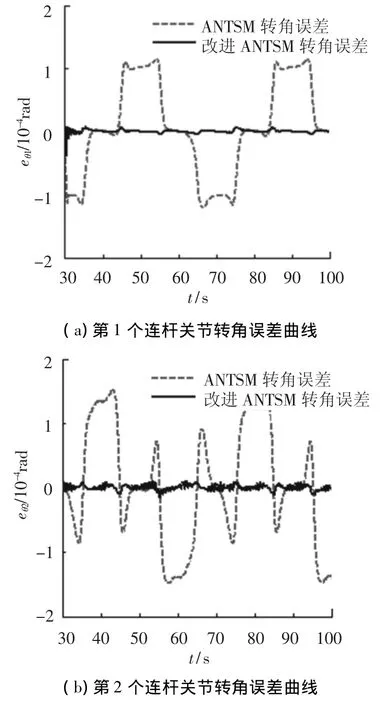
图6 载体姿态干扰条件下的关节转角误差曲线

5 结论

针对平面运动双连杆自由漂浮柔性空间机器人轨迹跟踪控制问题，本文设计了一种较为简单的控制终端滑模控制策略，能够在载体姿态干扰条件下跟踪关节期望轨迹，解决了带有柔性振动扰动的欠驱动空间机器人系统轨迹跟踪控制问题.最后，数值仿真研究结果表明所提出的控制方法能够很好的实现跟踪目标，且具有良好的鲁棒性和工程应用的潜在能力.

［1］TIAN Fu-yang，WU Hong-tao，SUN Hong-li.Efficient numerical integration method for dynamic of flexible space robots system［C］//2009 International Asia Conference on Informatics in Control，Automation，and Robotics.Bangkok:CAR，2009:102-106.

［2］YU Zhi-fu，YU Yong-bo，SHANG De-yong，et al.On orbit servicing flexible space robots dynamics and control during capturing target［C］//2010 International Conference on Measuring Technology and Mechatronics Automation.Changsha:ICMTMA，2010:817-820.

［3］KIRAN G S，KUMAR A，PATHAK P M，et al.Trajectory control of flexible space robot［C］//Proceedings of 2008 IEEE International Conference on Mechatronics and Automation.Takamatsu:ICMA，2008:738-743.

［4］ZHAO Hong-chao，CHEN De-qang.Optimal motion planning for flexible space robots［C］//Proceedings-IEEE International Conference on Robotics and Automation.Piscataway:IEEE，1996:393-398.

［5］丁希仑，王树国.空间机器人柔性臂的动力学轨迹跟踪控制［J］.机器人，1997，19(4):256-258.

［6］MUROTSU Y，TSUJIO S，SENDA K，et al.Trajectory control of flexible manipulators on a free-flying space robot［J］.IEEE，1992，12(3):51-57.

［7］王从庆，张承龙.自由浮动柔性双臂空间机器人系统的动力学控制［J］.机械工程学报，2007，43(10):196-200.

［8］洪昭斌，陈力.漂浮基柔性空间机械臂关节运动的拟增广自适应控制及柔性振动实时主动抑制［J］.振动与冲击，2010，29(1):200-206，247.

［9］GREEN A，SASIADEK J Z.Intelligent tracking control of a free-flying flexible space robot manipulator［C］//Collection of Technical Papers-AIAA Guidance，Navigation，and Control Conference 2007.Hilton Head:American Institute of Aeronautics and Astronautics，2007:132-156.

［10］CHU Ming，JIA Qing-xuan，SUN Han-xu.Global terminal sliding mode robust control for trajectory tracking and vibration suppression of two-link flexible space manipulator［C］//Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems.Shanghai:ICIS，2009:353-357.

［11］CHEN Wei，YU Yue-qing，ZHAO Xin-hua，et al.Dynamic control of the underactuated flexible robot in the operational space［C］//2009 IEEE International Conference on Mechatronics and Automation.Changchun:ICMA，2009:3223-3228.

［12］CAO Wen-jun，XU Jian-xin.Dynamic modeling and adaptive VSC of two-link flexible manipulators using a hybrid sliding surface［C］//Proceedings of the IEEE Conference on Decision and Control.Piscataway:IEEE，2000:5143-5148.

［13］WANG Yan-min，FENG Yong，YU Xing-huo.Fuzzy terminal sliding mode control of two-link flexible manipulators［C］//Proceedings of the 34th Annual Conference of the IEEE Industrial Electronics Society.Orlando:IECON，2008:1620-1625.

［14］翟艳霞，自由漂浮柔性空间机器人轨迹跟踪控制研究［D］.哈尔滨:哈尔滨工业大学，2011:1-16.

［15］陈志勇，陈力.柔性空间机械臂振动抑制的模糊终端滑模控制［J］.振动、测试与诊断，2010，30(5):481-486，592.

［16］CHEN Y，MEIROVITCH L.Control of a flexible space robot executing a docking maneuver［C］//Advances in the Astronautical Sciences.Reston，VA:AIAA，1993:756-766.

［17］FENG Yong，YU Xing-huo，MAN Zhi-hong.Non-singular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38(12):2159-2167.

［18］冯勇，鲍晟，余星火.非奇异终端滑模控制系统的设计方法［J］.控制与决策，2002，17(2):194-198.

［19］胡剑波，时满宏，庄开宇，等.一类非线性系统的Terminal滑模控制［J］.控制理论与应用，2005，22(3):495-498，502.

［20］赵文杰.不确定非线性系统的变结构控制研究［D］.保定:华北电力大学，2005:12-16.

［21］王艳敏.柔性机械手非奇异终端滑模控制方法的研究［D］.哈尔滨:哈尔滨工业大学，2009:9-15.

［22］LIU Shuang，MA Cai-wen，LUO Cui-hua，et al.Adaptive control of free-floating space robot with disturbance based on robust fuzzy compensator［C］//Proceedings of the 2nd International Conference on Intelligent Human-Machine Systems and Cybernetics.Nanjing:IHMSC，2010:23-28.

［23］颜闽秀.几类控制系统的若干滑模控制问题研究及应用［D］.沈阳:东北大学，2008:3-15.

［24］胡庆雷.挠性航天器姿态机动的主动振动控制［D］.哈尔滨:哈尔滨工业大学，2006:99-102.

［25］李军红，李兰君，阳武娇.采用可变边界层法削弱一类非线性变结构系统的抖振［J］.系统科学与数学，2008，28(9):1084-1091.

［26］SINGH A，KHALIL H K.Regulation of nonlinear systems using conditional integrators［J］.International Journal of Robust and Nonlinear Control，2005，15(8):339-362.

［27］SINGH A，KHALIL H K.State feedback regulation of nonlinear systems using conditional integrators［C］//Proceedings of the IEEE Conference on Decision and Control.Nassau:CDC，2004:4560-4564.

［28］SESHAGIRI S，KHALIL H K.Robust output feedback regulation of minimum-phase nonlinear systems using conditional integrators［J］.Automatica，2005，41(1):43-54.