一种汽车防抱死制动系统的非线性控制方法
2012-09-02刘志远井后华
刘志远,井后华,陈 虹
(1.哈尔滨工业大学控制科学与工程系,150001哈尔滨;2.吉林大学控制科学与工程系,130022长春)
防抱死制动系统(anti-lock braking system,ABS)主要用于在紧急制动过程中通过调节制动力矩防止车轮抱死,在保持转向能力和横向稳定性的同时最大利用路面的摩擦力,从而有效提高行车安全性[1].ABS控制相关的大多数研究均基于制动力矩可以连续精确调节的假设[2-3],这与实际情况不符.由于受成本和可靠性因素制约,实际车辆中广泛采用开关阀调节压力.通过协调阀的开、关,这类执行器可以实现增压、保压、减压三种控制模式.为此,需要设计其切换规则来实现制动力矩和滑移率的调节.工程中广泛采用基于逻辑和参数阈值设计控制规则[1],这种方法进行参数整定时需要经验和进行大量的试验,导致开发周期长、费用高.文献[4-5]分别以不同相平面为基础,参考相轨迹特点定性地分析和设计不同工作模式之间的切换规则.但由于这些规则主要基于轮加速度设计,而忽略了滑移率控制的本质,所以会造成制动力矩和滑移率剧烈波动,从而降低制动过程的平顺性.
本文采用切换系统模型描述了开关阀ABS增压、保压、减压三种工作模式的动态特性;并基于Filippov意义下的Lyapunov方法设计出两个切换面,以其对状态空间的划分形式作为切换规则;结合基于整车动力学软件veDYNA的仿真对比,对控制器进行了分析和改进;最后通过道路实验进行验证.
1 开关阀ABS建模
轮胎-地面之间的纵向摩擦系数μ是分析制动效能的主要依据,受到许多因素影响,但其主要表现为依赖于滑移率λ的强非线性关系.图1给出了一条典型的μ-λ曲线.为了保证制动性能,要求控制滑移率λ在曲线峰值附近.据此,ABS的本质实际上是通过执行器实现对各车轮滑移率的调节.
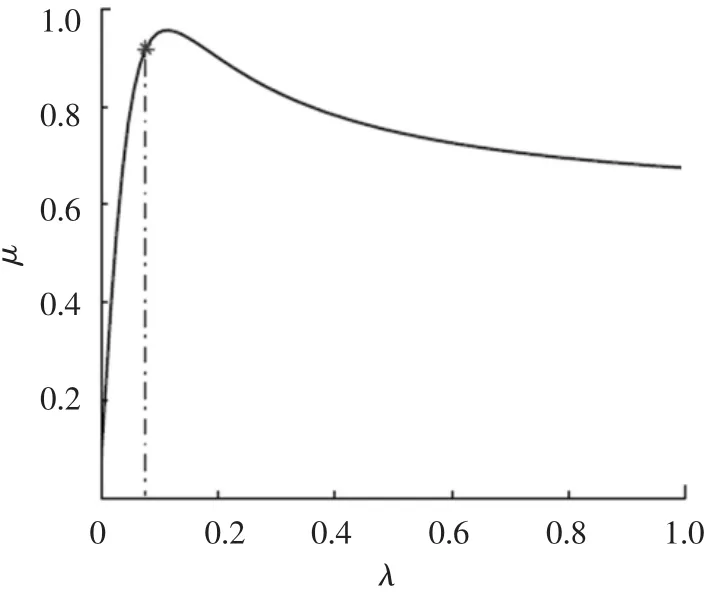
图1 典型μ-λ曲线
滑移率定义为λ=1-ωr/v,其中ω是车轮角速度,r是有效车轮转动半径,v是车辆纵向速度.基于1/4车辆模型,可得滑移率动态方程[2]为
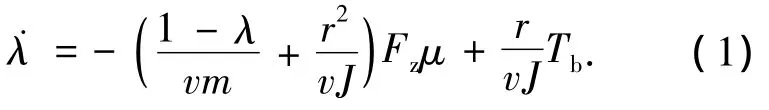
其中:m是1/4车辆质量;J是车轮转动惯量;Fz是地面对车轮的支持力;Tb为施加在制动盘上的制动力矩.考虑到惯量差异悬殊,为了便于控制器设计,忽略车速动态特性,而将车速作为慢变参数处理[2].
由于1/m≪r2/J,式(1)可进一步简化为

制动力矩Tb通常采用液压(气压)制动系统实现,与轮缸内液压成正比.系统为每个轮缸分配一对阀体分别用于进液和出液,通过协调控制两个阀体的开关可实现增压、保压、减压三种工作模式[1].然而,由于开关阀不能调节流量,导致力矩变化率不能任意调节.考虑到ABS制动过程中压力波动范围很小,忽略其非线性特性.因此,近似认为三种模式分别对应3个不可调节的常值力矩变化率,而将执行机构主要特性描述为[6-7]

其中γ1、γ2均为正值,分别为增压和减压模式的力矩变化率.
设期望滑移率λ*,令x1=λ-λ*,x2,,且定义Kλ=∂μ(λ)/∂λ|λ=λ*,0,由式(2)、(3)可得关于车速v的参变系统描述为

为了充分利用地面附着力并保证制动平顺性,选择λ*在峰值点左侧且接近峰值点处,此时满足rFzKλ+Ja/r>0[8].为简便起见,定义η=rFzKλ+Ja/r,x=[x1x2]T,系统(4)简写为

其中u∈{γ1,0,-γ2}为不连续变量.所以g(x,v,γ1)、g(x,v,0)、g(x,v,-γ2)分别表示对应于增压、保压、减压三种工作模式的子系统.
ABS的控制原理就是通过协调各工作模式之间的切换,将滑移率控制在期望点附近.因此,本文的控制问题可归结为设计3个子系统之间的切换规则,以实现闭环系统的渐进稳定.
2 控制器设计
近年来,多模型切换系统控制已引起国内外学者的重视,并在许多领域进行了广泛的应用.对于本文所研究的一类切换系统,其主要通过设计各子系统之间的切换律来实现整个系统的稳定控制.切换律按表现形式一般分为两类:其一,以切换时刻作为控制变量,即考虑某性能指标的优化问题[9],但该方法实时性和鲁棒性较差;其二,在状态空间中构造切换面,以其划分形式作为切换基准[10],该方法具有状态反馈特征,更易于实现,且鲁棒性较强.为此,本文将从切换面角度考虑开关阀ABS控制律设计问题.
2.1 切换面构造
针对本文3个子系统的特征,g(x,v,0)是介于g(x,v,γ1)和g(x,v,-γ2)之间的中间状态,为此,定义两个切换面分别作为g(x,v,0)与其他二者之间的切换条件.如图2所示,在状态空间中,两个切换面S1={x|s1(x,v)=0}、S2={x|s2(x,v)=0}表现为经过原点的不重合曲面,其中s1(x,v)、s2(x,v)均为连续可微的状态反馈函数.两切换面将状态空间分为3个子空间P1={x|s1(x,v)>0}、P2={x|s1(x,v)<0,s2(x,v)>0}、P3={x|s2(x,v)<0}分别表示g(x,v,γ1)、g(x,v,0)、g(x,v,-γ2)3个子系统的工作区域.
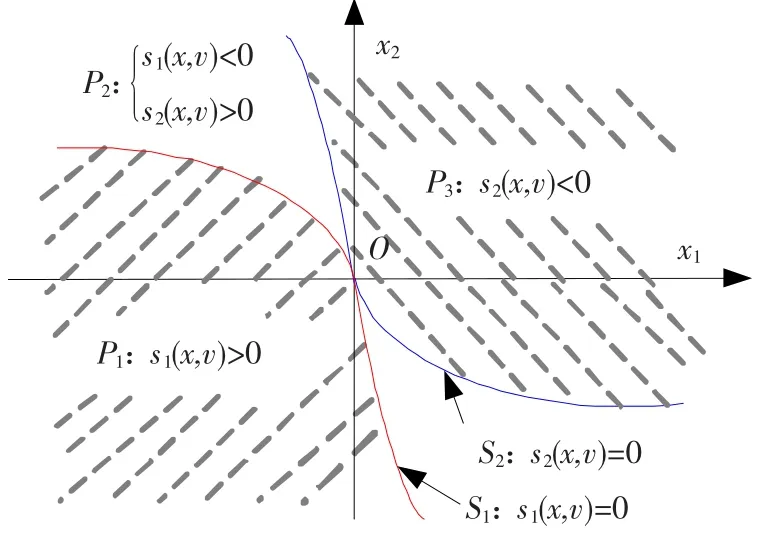
图2 切换面状态空间划分
2.2 反馈函数求解
为从理论上保证上述切换面作用下的闭环系统能够稳定,本文将采用Lyapunov方法作为切换面解析解的求解依据.由于系统在切换面处是不连续的,导致传统连续系统分析方法不再适用.为此,本文将在Filippov解的意义下进行分析.针对非连续微分方程,Filippov给出了一种微分包含解定义,用微分包含替代原微分方程来研究解问题,从而可以克服在经典解框架下无法给出非连续处解的问题[11].本文闭环系统在Filippov意义下的微分包含形式记为∈K[g](x,v).对于切换面上的点,Filippov集合K[g](x,v)为其无限小邻域内两侧矢量的凸组合.以x∈S1为例,K[g](x,v)={g(x,v,γ1),g(x,v,0)}=g(x,v,[0,γ1]).其中表示凸闭集,而对于切换面外的点,则与经典连续系统一致.因此,参照图2,可以得到
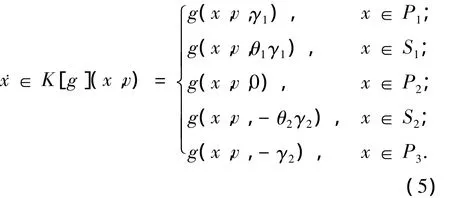
其中θ1、θ2∈[0,1]表示g(x,v,u)在两个不连续处的u值分别对应集合[0,γ1]和[-γ2,0].
为了保证Filippov解的存在性和唯一性[11],其中一种充分条件为

对于∀x≠0.
根据式(6),可初步构造s1(x,v)、s2(x,v)为
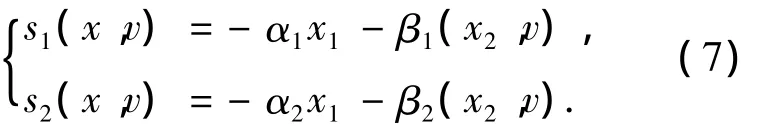
其中α1>0,α2>0,

下面基于Filippov意义下的Lyapunov方法[12]确定状态反馈函数s1(x,v)、s2(x,v).根据图2所示的空间划分方式,选取Lur’e-Postnikov类型的非平滑Lyapunov函数[13]

V(x,v)呈类能量形式,即包含1个二次型函数的“动能”和1个与执行器和反馈函数相关的“势能”.
由于Lyapunov函数具有非平滑特性,需采用广义时间求导方法,记为(d/dt)V(x,v)∈据此分别在5个子空间(S1、S2、P1、P2、P3)中计算·~V(x,v),结果如式(9)所示.方便起见,下文中将β1(x2,v)和β2(x2,v)分别简写为β1和β2.

其中对于x∈S1、S2,即状态x保留在切换面上的情况,由1(x,v)、2(x,v)=0可得
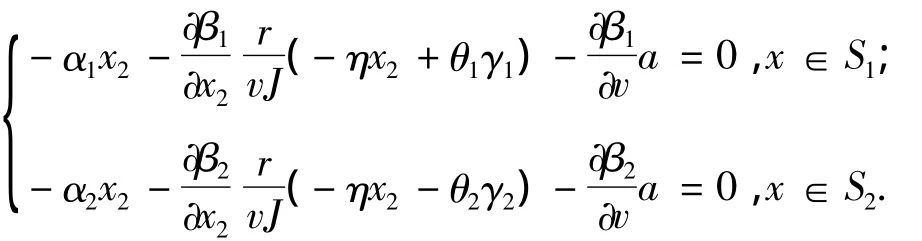
则式(7)、(9)可以作为反馈函数s1(x,v)、s2(x,v)的求解依据.以s1(x,v)为例,除α1>0,∂β1(x2,v)/∂x2≥0外,还要考虑(x,v)≤0的条件:
1)对于x∈P2,(x,v)≤0必然成立;
2)对于x∈P1,(x,v)≤0的1个充分条件为
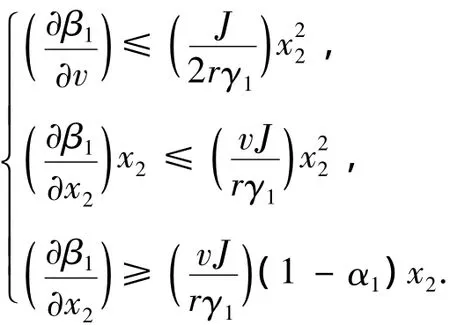
而对于x∈S1,即x保留在切换面S1上时,(x,v)≤0的1个充分条件为α1x22+ax2(∂β1/∂v)≥0.
综上可以得到一组保证·~V(x,v)≤0的s1(x,v)可行解
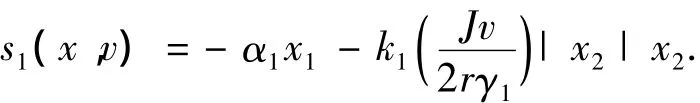
式中α1>0,k1≥0;对于x2≥0,1≥k1≥1-α1;对于x2<0,k1≥α1-1.s1(x,v)在原点处连续可微.若令α1=α2=1,则可得s1(x,v)和s2(x,v):(a)对于x2≥0,

其中0≤k21≤k11≤1.(b)对于x2<0,
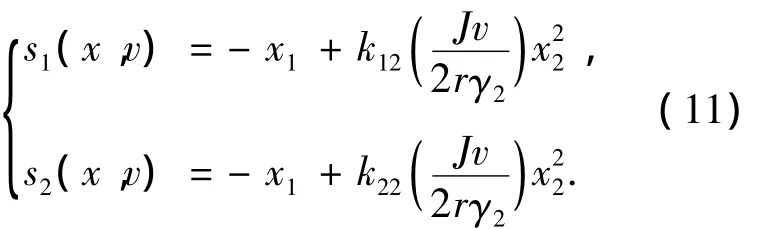
其中0≤k12≤k22≤1.
因此,在式(10)、(11)所定义的反馈函数s1(x,v)和s2(x,v)的作用下,在任意初始状态下均有(x,v)≤0,且(x,v)=0仅在x2=0时成立.而从闭环系统特性(5)看,轨迹不会停留在x2=0上除原点以外的其它点.所以,闭环系统状态将逐渐收敛至原点.
2.3 控制器实现
上述分析表明,基于式(10)、(11)得到的两个切换面S1={x|s1(x,v)=0}和S2={x|s2(x,v)=0}可以保证闭环系统原点的渐进收敛性,满足控制需求.为更清晰表述控制器实现方式及其与ABS工程问题的关联,可进一步将控制器表示为图3所示的状态.

图3 状态转移示意
3 控制器分析及仿真
由式(10)、(11)可看出,反馈函数中包含车速v,说明其可根据速度变化进行增益调度,从而可以适应制动过程中车速的大范围变化.此外,除车辆参数(J、r、γ1、γ2)以外,切换面仅包含4个设计参数,即k11、k12、k21、k22.而这4个参数主要用于调节切换面的倾斜度,即通过改变状态空间的划分形式来调整切换策略.为了清晰说明这一点,本节将基于德国Tesis公司的高精度车辆动力学仿真软件veDYNA进行仿真.仿真环境模拟干燥柏油路面,制动初速度100 km/h,期望滑移率为0.11,且当滑移率大于0.15时激活控制器;限于篇幅,仅给出左后车轮仿真结果,各子图依次为滑移率(-)、轮缸中制动压力(MPa)、工作模式(1、0、-1分别表示增压、保压、减压).由于每组仿真均为两组以上参数的对比结果,且车速、轮速极为接近,难以分辨,因此仿真结果未给出二者曲线;另外,为了清晰地对比说明参数作用,仅给出最初1 s的仿真结果;完整的制动过程和车速、轮速对比曲线将在后续实车道路试验部分给出.控制器主要参数如表1所示.
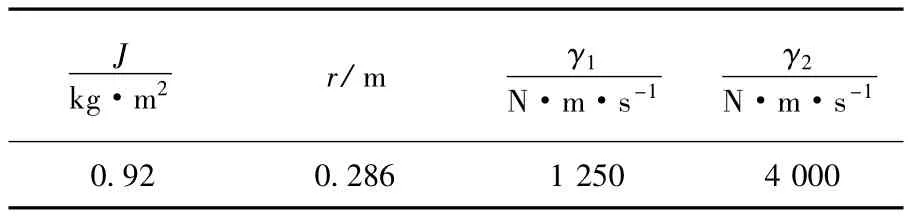
表1 控制器主要参数
3.1 参数k11、k22特性分析
调整增益k11可以改变切换面S1的倾斜度,进而调整“增压-保压”的切换时刻.较小的k11会使增压区域增大而将保压时刻滞后,这会造成控制过程增压过度;相应地,增大k11会使“增压-保压”切换时刻提前,避免液压的明显超调.同理可以分析k22.
图4给出了在k21=k12=0条件下,k11、k22相等且依次等于1、0.25、0时的仿真结果,其中线条分别为黑色实线、蓝色虚线和红色点划线.可以看出,当4个增益均为0,即两个切换面合并为纵坐标时,增压和减压模式反复切换,压力和滑移率波动严重;而随着k11、k22不断增大,两切换面相互分离,作为增压和减压之间的过渡模式,保压对应子空间增大,液压和滑移率波动减弱,踏板感觉和制动平顺性会相应地有所改善.

图4 不同控制参数k11、k22下的仿真结果
3.2 参数k21、k12特性分析
类似地,k21、k12分别用于调节“保压-减压”、“保压-增压”的切换时刻.清晰起见,图5仅给出k11=k22=1,k21、k12相等且分别为1、0的仿真结果.
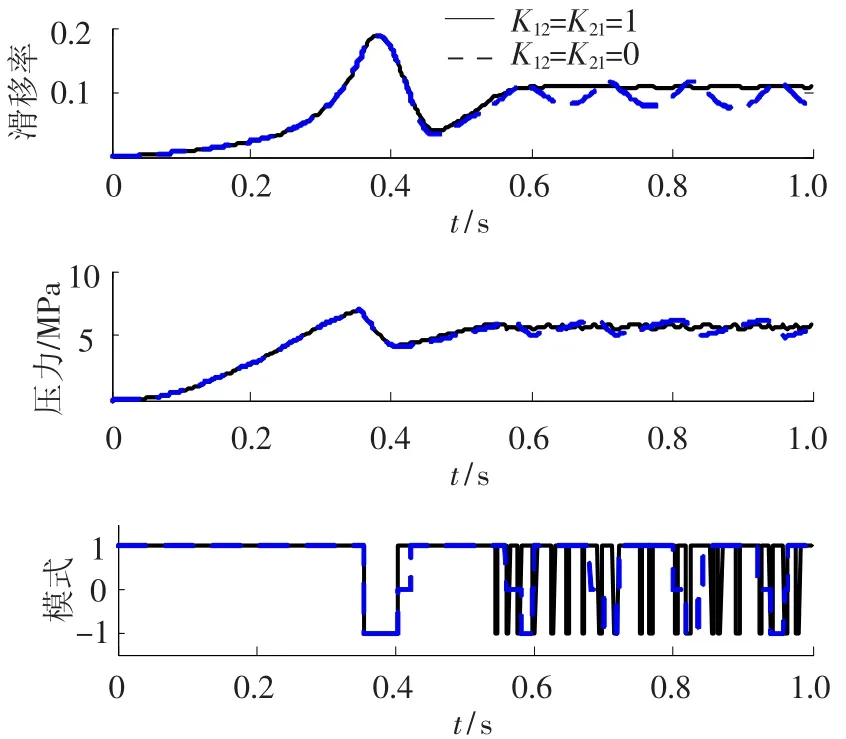
图5 不同控制参数k21、k12下的仿真结果
k21、k12为0时,由保压模式进入调压模式(增压或减压)的时刻较晚,而且调压模式对应的子空间较小,致使压力和滑移率存在明显的波动.随着k21、k12逐渐增大,两切换面逐渐靠近,保压子空间减小,快速的增压和减压可以减小压力和滑移率的波动幅度;然而,相应的保压时间也逐渐减少,必然导致阀频繁开关,这种驱动方式会严重影响阀的性能和使用寿命,并且在实际中很难实现.特别地,当4个增益均为1时,两切换面重合,保压区间消失,即仅依靠增压和减压模式进行压力调节,此时的切换面作用与滑模面类似[14].
4 控制器改进及实验验证
4.1 控制器改进
根据上节分析,增益参数(k11、k12、k21、k22)不仅用于调整滑移率跟踪效果,同时又影响各工作模式的切换频率;但两个性能相互制约,难以同时满足;这是由其原点稳定的控制目标决定的.考虑到相比于精确的滑移率控制,能够用少量的切换将滑移率平稳控制在期望值附近更具有实际意义.因此,下面将控制目标调整为控制滑移率收敛到期望值的指定邻域内,即考虑平衡集合的收敛问题.
如图6所示,将切换面S1向x1轴负向移ε,其与x1轴交点为A.参考Lyapunov函数(8),P3不变,V(x,v)仍为原点的Lyapunov函数,V(x,v)递减可以保证状态轨迹向原点收敛;而P1={x|s1(x,v)>ε}中V(x,v)变为点A的Lyapunov函数,V(x,v)递减可以保证状态向点A收敛;此外,P2={x|s1(x,v)<ε,s2(x,v)>0}中状态轨迹向横坐标收敛.综上,在切换面S1、S2作用下,状态轨迹将最终收敛至横坐标上点A和原点所限定的集合,即


图6 改进切换面作用下平衡域的收敛
ε决定着收敛区间的大小,其选取会影响到闭环系统的控制性能.如图7所示,其中黑色实线和蓝色虚线分别表示ε为0.04和0.02,即期望滑移率分别为0.07~0.11,0.09~0.11的仿真结果.可以看出,闭环系统可以通过少数的切换就将状态收敛到期望平衡域中,改善了制动的平顺性.然而,如果ε过大会导致滑移率距最佳期望值0.11较远,而降低制动效率.因此,需要在综合考虑制动效率、执行器特性等多方面因素基础上折中选择ε.
4.2 实验验证
实车测试系统使用一汽红旗明仕CA7180A4E车型作为试验车,采用原车轮速传感器测量轮速,以此估计车速并计算得到滑移率,为各车轮轮缸安装压力传感器以获取液压信息,采用dSPACE AutoBox实现控制器.实验中AutoBox通过信号调理板和与传感器相连,根据测量信息和控制律确定控制信号,并通过驱动电路调节液压控制单元中阀体开关状态,实现对制动力矩的调节;同时AutoBox实时采集所有可测量信号.
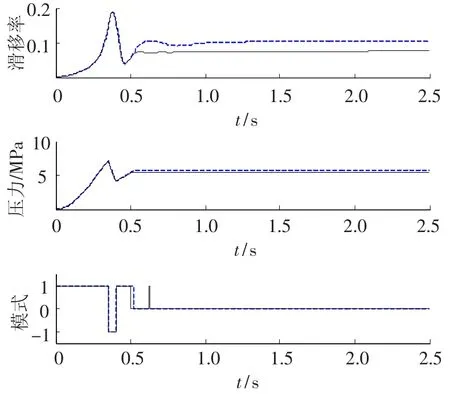
图7 不同平衡域下的仿真结果
在干燥柏油路面以初速度60~70 km/h进行紧急制动测试.下面同样给出左后车轮测试结果,与仿真结果相比,实验结果给出了完整的制动过程以及车速、轮速的对比曲线,以便于更直观分析整个制动过程.
测试1:令k11、k12、k21、k22=1,λ*=0.11,ε=0.02,即期望滑移率为0.09~0.11,实验结果如图8所示.可以看出,由于实际车辆和工况比仿真环境更为复杂,包括很多未建模特性和扰动、噪声,实际中的参考车速和真实值存在一定偏差,这些因素造成了该闭环系统状态并没有维持在期望滑移率区间中,而是在其附近波动,表现为与常规ABS类似的控制效果,但是依然很好地实现了防抱死制动的控制目标.需要指出,受传感器特性和路面影响,低速情况下轮速测量和车速估计误差明显,致使滑移率出现较大偏差,因此滑移率计算和控制效果均会受到影响.然而由于此时车速较低,因此对整个制动过程的控制性能影响不大;另外,实际应用中也可以采取适当修正处理来改善低速控制效果.
测试2:另一方面,对于实际环境中存在的不确定性、噪声、车速估计误差等因素,可以通过适当调整参数,一定程度上减少阀开关次数,改善制动的平顺性.图9所示为设置ε=0.04,即期望滑移率为0.07~0.11时的实验结果.其中,滑移率曲线峰值达到0.3,主要是由于进入ABS之前的人为制动操作差异引起,进而造成后续ABS控制过程中液压也出现了较大波动.与图8的主要区别是由于滑移率收敛域增大,一定程度上提高了系统对滑移率计算偏差的鲁棒性,使得后续制动过程中滑移率响应曲线略微降低,但可迅速收敛并保持在该收敛区间内,以此避免阀的频繁切换,并获得平顺的制动效果;但由于滑移率收敛域下限减小,使得制动效率略受影响.因此,控制器调整依据是以牺牲制动效率为代价,通过适当放大ε来获取更大的鲁棒性和适应性.参考前文的仿真分析,实际中需要综合考虑实际滑移率误差、制动效率、控制模式切换频率、制动平顺性等关系的折中处理选择ε.

图8 干燥沥青路面实验测试1

图9 干燥沥青路面实验测试2
测试3:目前实际应用中开关阀ABS仍然采用逻辑门限方法,图10给出了一组原车ABS的实验测试曲线,其中车速测量偏差造成滑移率曲线不够准确.原车ABS的控制原理主要是以轮加速度为主、滑移率为辅,通过设计逻辑关系和参考阈值控制滑移率在图1所示的μ-λ曲线峰值点附近作类周期性运动,以此获取近似的滑移率控制效果[1].如图10所示,设计原理的差异导致该ABS策略作用下的制动过程中执行器工作模式反复切换,进而造成液压反复波动调节,因此制动踏板感觉和制动平顺性会受到影响.另外,由于该方法逻辑复杂,参数较多,在应用中需要经验和进行大量的试验,导致开发周期长,费用高.与其相比,本文控制方法以滑移率峰值点左侧为主要工作区域,基于滑移率动态模型设计而来,峰值点左侧滑移率区间收敛控制目标可以避免工作模式的频繁切换,从而提高制动踏板感觉和制动平顺性;而且本文控制器形式简单,待配置参数较少.文献[15]采用本文控制器的一种特殊形式,进行了大量的仿真和实验,对方法的实用性和有效性进行了检验.需要指出,原车ABS对复杂的操作方式和工作环境均具有很好的适应性,而目前本文方法研究工况相对单一,因此还需要更为深入的研究方可满足实际复杂工况的要求.
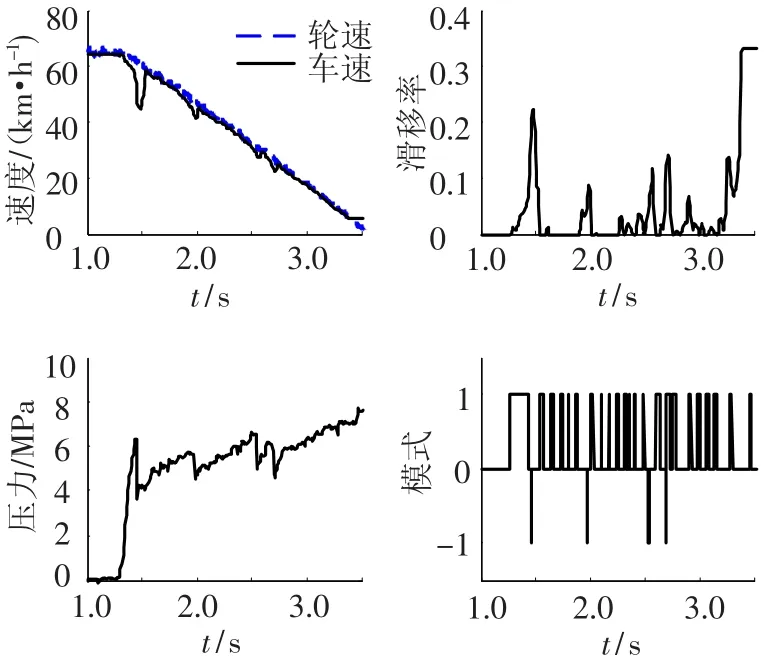
图10 原车ABS控制器实验测试
5 结论
1)讨论了开关阀ABS的动态特性,给出了一种具有滑移率连续动态和执行器不连续动态的切换系统模型,并将其控制问题转换为切换系统镇定问题.针对开关阀ABS的非连续动态,引入Filippov概念,给出了一种微分包含解定义,解决了经典解框架下无法给出非连续处解的问题.
2)提出的以状态空间划分作为增压、保压、减压三种工作模式之间切换规则的非线性控制器设计方法,能够保证闭环系统的稳定性,且满足系统的鲁棒性要求.考虑到实际应用的需求,将控制目标调整为平衡区域的收敛控制问题,降低了控制过程的切换频率.
3)与现有控制器相比,本文的方法具有控制律形式简单、控制参数少,参数物理意义明确和易于配置的特点.仿真与实验结果表明,本文的方法具有高效和平顺的制动性能.
[1]顾柏良.Bosch汽车工程手册[M].北京:北京理工大学出版社,1998:712-772.
[2]JOHANSEN T A,PETERSEN I,KALKKUHL J,et al.Gain-scheduled wheel slip control in automotive brake systems[J].IEEE Transaction on Control and System Technology,2003,11(6):799-811.
[3]TANELLI M,ASTOLFI A,SAVARESI S.Robust nonlinear output feedback control for brake-by-wire control systems[J].Automatica,2008,44(4):1078-1087.
[4]MORSELLI R,ZANASI R.Self-tuning control strategy for antilock braking systems[C]//Proceedings of the American Control Conference.Piscataway:IEEE,2006:5861-5866.
[5]PASILLAS-LEPINE W.Hybrid modeling and limit cycle analysis for a class of five-phase anti-lock brake algorithms[J].Vehicle System Dynamics,2006,44(2):173-188.
[6]KUO C Y,YEH E C.A four-phase control scheme of an antiskid brake system for all road conditions[J].Proc IMechE,Part D:J Automobile Engineering,1992,206(4):275-283.
[7]TANELLI M,OSORIO G,BERNARDO M,et al.Existence,stability and robustness analysis of limit cycles in hybrid anti-lock braking systems[J].International Journal of Control,2009,82(4):659-678.
[8]OLSON B J,SHAW S W,STEPAN G.Nonlinear dynamics of vehicle traction[J].Vehicle System Dynamics,2003,40(6):377-399.
[9]EGERSTEDT M,WARDI Y,DELMOTTE F.Optimal control of switching times in switched dynamical systems[C]//Proceedings of the 42th IEEE Conference on Decision and Control.Piscataway:IEEE,2003:2138-2143.
[10]BACCIOTTI A.Stabilization by means of state space depending switching rules[J].Systems&Control Letters,2004,53(3/4):195-201.
[11]FILIPPOV A F.Differential Equations With Discontinuous Right-hand Sides[M].Boston:Kluwer Academic Publishers,1988:48-122.
[12]SHEVITZ D,PADEN B.Lyapunov stability theory of nonsmooth systems[J].IEEE Transaction on Automatic and Control,1994,39(9):1910-1914.
[13]AKASAKA D,LIU K Z.Nonlinear feedback control of a class of on-off control systems:an approach based on analytical solution of PDEs[C]//Proc IEEE Conf on Decision and Control.Piscataway:IEEE,2007:86-91.
[14]DRAKUNOV S,OZGUNER U,DIX P,et al.ABS control using optimum search via sliding modes[J].IEEE Transaction on Control and System Technology,1995,3(1):79-85.
[15]JING H H,LIU Zh Y,CHEN H.A switched control strategy for anti-lock braking system with on/off valves[J].IEEE Transactions on Vehicular Technology,2011,60(4):1470-1484.
