基于偏序关系的区间数多属性决策方法研究

宋晓辉

（郑州华信学院 基础教学部，河南 郑州 451100）

基于偏序关系的区间数多属性决策方法研究

宋晓辉

（郑州华信学院 基础教学部，河南 郑州 451100）

针对权重和属性值都是区间数的多属性决策问题，基于三种常用的偏序关系，讨论综合评价值的排序，选出最优方案.当综合评价值有最大元时，最大元对应的方案就是最优方案；当综合评价值没有最大元时，通过定义拟最大元找到最优方案.最后给出了一个实例分析.

区间数；多属性决策；偏序关系；最优方案

1 引言

多属性决策问题是指在考虑多个属性的情况下，选择最优方案或进行方案排序的决策问题，它是决策科学的一个重要组成部分.在现实的决策问题中，由于客观事物的复杂性和不确定性以及人们认识事物的模糊性，导致决策信息不确定，可以用区间数进行量化，因此对基于区间数的多属性决策问题研究具有重要意义.多属性决策问题最终归属于对各方案进行排序或择优.当各方案的综合评价值用区间数表示时，我们在区间数集上引入偏序关系，就可以对各个方案进行排序.本文基于三种常用的偏序关系,讨论了综合评价值的排序，并通过实例分析得知当决策者的心态不同时，得到的最优方案也可能不一样，符合人们的一般认识.

2 区间数及其序关系

定义2.1[1]设=[a-,a+]是有界闭区间，如果a-,a+∈R，则称軇=[a-,a+]为区间数.实数集R上的全体区间数记为IR，即

特别地，记I+R={[a-,a+]|0≤a-≤a+，a-,a+∈R}为正区间数集.本文讨论的区间数都是正区间数.

当a-=a+时，记[a-,a+]={a-}=a-.可见，实数是区间数的特殊情况.

定义2.2[2]设P是一个集合，P上的二元关系≤叫做一个偏序关系，如果满足

这时称(P,≤)为一个偏序集.

下面是人们常用的几种区间数偏序关系.

3 基于区间数的多属性决策问题描述

本文研究属性的权重和方案在各属性下的属性值都是区间数的情形，为了方便起见,作以下标记：

.S={S1,S2,…,Sm}：m个决策方案的集合（m≥2）.

.Q={Q1,Q2,…,Qn}：n个属性(或指标)的集合（n≥2）.

在决策中,属性大致可以分为两类,即效益型属性和成本型属性.为了消除不同量纲或数量级给决策结果带来的诸多不便，可以采用以下规范化方法,得到决策矩阵其中也是区间数.

对于效益型属性[3]：

对于成本型属性[3]：

区间数多属性决策问题就是在区间数决策信息(即w軒和A軒)已知的情况下,如何从备选方案的集合S中选择最优方案或对方案进行排序.本文主要通过对各方案的综合评价值的排序，来反映各方案的优先顺序，关于综合评价者的求取方法详见文献[4].

4 区间数的排序

在得到各个方案的综合评价值后，接着就是对综合评价值进行排序，选出最优方案.由于这里的每一个综合评价值都是区间数，因此本文应用偏序关系对综合评价值进行排序.其基本思想是：如果综合评价值有最大元，则最大元对应的方案为最优方案；如果综合评价值没有最大元，则定义拟最大元，分别求出每个极大元与拟最大元的距离.如果一个极大元离拟最大元距离最小，则这个极大元对应的方案为最优方案.

这里D的上确界M不属于集合D，若不然，则M就是最大元，D有最大元.类似地，可定义偏序集(D,≤2)的拟最大元M'，偏序集(D,≤3)的拟最大元M".

设S={S1,S2,…,Sm}为m个决策方案的集合…，}为方案综合评价值的集合，其中]为方案Si的综合评价值.下面说明集合在三种偏序关系≤1、≤2、≤3下上确界的存在性.

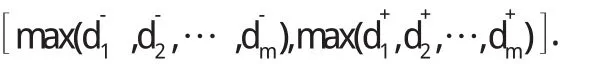
证明 令

假设N=[N-,N+]是集合D的上界，则有，即M≤1N，M是集合D的最小上界.

由上确界的定义知，M是集合D在序关系≤1下的上确界.

证明 令

假设N=[N-,N+]是集合D的上界，则有，即M'≤2N，M'是集合D的最小上界.

由上确界的定义知，M'是集合D在序关系≤2下的上确界.

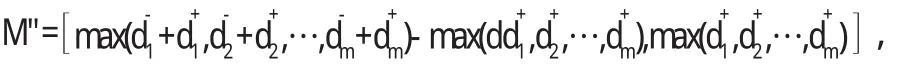
假设N=[N-,N+]是集合D的上界，则有，即M"≤3N，M"是集合D的最小上界.

由上确界的定义知，M"是集合D在序关系≤3下的上确界.

定义4.2[5]设任意的]定义映射d:IR×IR→如下：这里的t∈[0,1]，则称之间的距离.

区间数排序步骤：

S t e p 1选择≤1、≤2、≤3其中一个序对各个方案的综合评价值进行排序.

S t e p 2若综合评价值有最大元，则最大元对应的方案为最优方案.若综合评价值没有最大元，则虚构拟最大元M.

S t e p 3只考虑作为拟最大元下邻的那些极大元，依次设为d'1，d'2，…，d'n(1≤n≤m).计算d'i(1≤i≤n)与拟最大元M之间的距离d(d'i,M)，若d'i比d'j(1≤i,j≤n)离拟最大元M距离小，则d'i优于d'j.

S t e p 4方案决策者根据d(d'i,M)(1≤i≤n)的大小，选出最优方案.若d(d'i,M)越小，则d'i对应的方案S'i越优.

分析：当方案集没有最大元时，须定义拟最大元，三种偏序关系有三种不同的拟最大元，而通过距离得到的最优方案有可能不一样.如果两个方案具有≤1序关系，则一定具有≤2和≤3序关系.采用≤2序关系的决策者持保守心态，它只考虑左端点和中点是否具有相同的大小关系，所以通过序关系得到的最优方案也是一种保守的结果.采用≤3序关系的决策者持积极心态，它只考虑右端点和中点是否具有相同的大小关系，所以通过≤3序关系得到的最优方案也是一种积极的结果.故采用三种偏序关系≤1、≤2、≤3分别体现了决策者的中立、保守、积极的心态.

5 实例分析

为了了解各学院的实际情况和促进各学院的发展，某大学决定对5个学院(S1,S2,S3,S4,S5)进行评估.大学组织了专家组，拟采用教学、科技、服务三个属性作为评估指标，经过调查和统计，得到各属性的权重和各方案的属性值见表1[6]和表2[6]，试做出综合评估.

表1 属性的权重

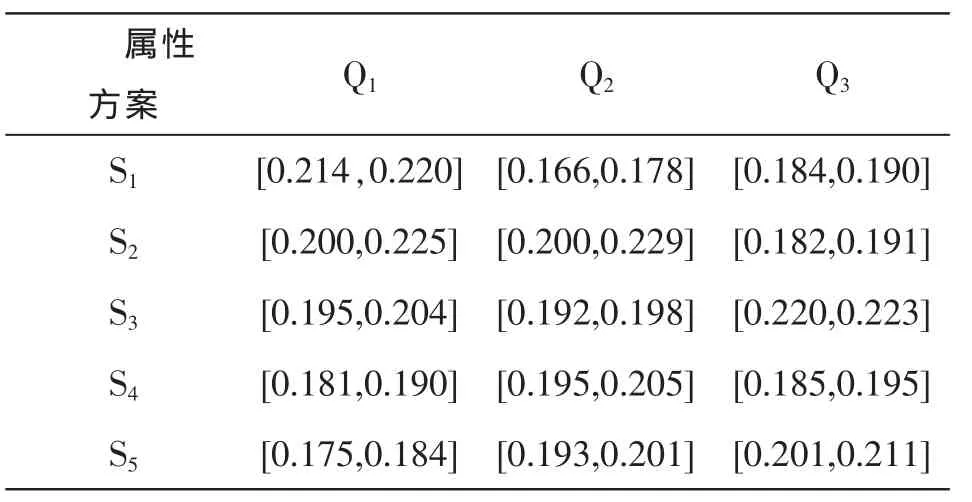
表2 各方案的属性值

因三个属性都是效益型的，且决策矩阵已规范化.根据文献[4]可计算每个学院的综合评价值分别为：

①基于偏序关系≤1的排序，这时决策者持保守态度.

利用≤1对}进行排序，得到)，其中无法比较和为极大元.

②基于偏序关系≤2的排序，这时决策者持中立态度.

利用≤2对}进行排序，得到，其中和无法比较.由此可知，S3为最优方案.

③基于偏序关系≤3的排序，这时决策者持积极态度.

利用≤3对}进行排序，得到，其中和无法比较和为极大元.

分析：结果表明，当决策者的心态不同时，得到的方案排序结果也会不同，是符合实际的.当决策者持中立态度和持保守态度时，认为S3为最优方案.当决策者持冒险态度时，认为S2为最优方案.

6 结束语

本文主要对基于区间数的多属性决策方法进行了研究，通过对各方案综合评价值的比较，来反映各方案的优先顺序.首先基于三种常用的偏序关系对各方案综合评价者进行比较，当综合评价值有最大元，则最大元对应的方案为最优方案；当综合评价值没有最大元，则定义拟最大元.分别求出每个极大元与拟最大元的距离，如果一个极大元离拟最大元距离最小，则这个极大元对应的方案为最优方案.三种偏序关系的选择反映了决策者的不同心态，当决策者持不同心态时，得到的最优方案可能不同，是符合实际的.

〔1〕胡宝清.模糊理论基础[M].武汉：武汉大学出版社,2004.

〔2〕黄天民.格序引论及其应用[M].成都：西南交通大学出版社,1998.

〔3〕汪新凡.区间数多属性决策的SPA-TOPIS方法[J].湖南工业大学学报,2008（1）:62.

〔4〕宋晓辉.基于区间数的多属性决策方法研究.西南交通大学硕士学位论文,2011.

〔5〕兰蓉.一种基于区间数距离的理想点多属性决策方法[J].西安邮电学院学报,2009,1(14):84-85.

〔6〕郭春香,郭耀煌.具有区间数的多目标格序决策方法研究[J].预测,2004（5）:71-73.

O 29

A

1673-260X（2012）10-0010-03