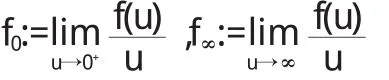时标上高阶动力方程边值问题正解的存在性

何红军

（郑州华信学院 基础教学部，河南 郑州 451100；许昌实验小学，河南 许昌 461000）

时标上高阶动力方程边值问题正解的存在性

何红军

（郑州华信学院 基础教学部，河南 郑州 451100；许昌实验小学，河南 许昌 461000）

本文研究了一类时标上高阶动力方程m点边值问题

其中T是时标，aj∈[0,+∞]，ξj∈[0,ρ(T))T是满足适当条件的常数.利用泛函型锥上压缩拉伸不动点定理，得到该问题的正解存在性，并且推广了一些原有的结果.

不动点；锥；格林函数；正解

1 引言和假设

由于动力方程的重要性和深刻性，关于动力方程边值问题的研究受到广大学者的关注.例如在文［1］中利用上下解法，得到二阶三点边值问题的正解，在文［2］［3］中使用不动点指数，不动点定理，得到二阶m-点边值问题正解存在性，在文［4］中研究了：

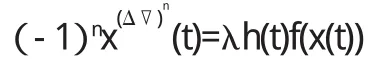
受上面学者研究工作的启发，本文对如下问题进行了研究：

其中aj>0,ξj∈(0,ρ(T))T，σn-1(0)<ρn-1(ξj)，σn-1(ξj)<ρn-1(T)，λ>0我们做如下基本假设

(H2)f(x)是正函数，a:[0,T]→[0,+∞]且a(t)≠0,t∈[0,T]

2 引理及定理

先考虑

的格林函数，当y(t)=0时，(3)(4)有唯一解为0，则(3)(4)的格林函数存在.

引理1设w≠0则(3)(4)有唯一解

证可以验证(5)满足(4)

对(5)两端△-可微，得

再对上式两端塄-可微，则u△塄(t)=-y(t)证毕.

引理2设w≠0，则(3)(4)的格林函数为

证 当t∈[0,ξ1]时，根据(5)式

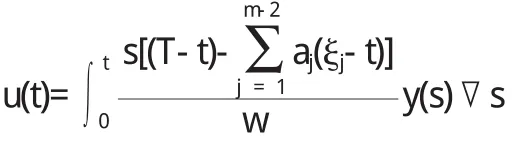
当t∈[ξr-1,ξr]，2≤r≤m-2时，由(5)式

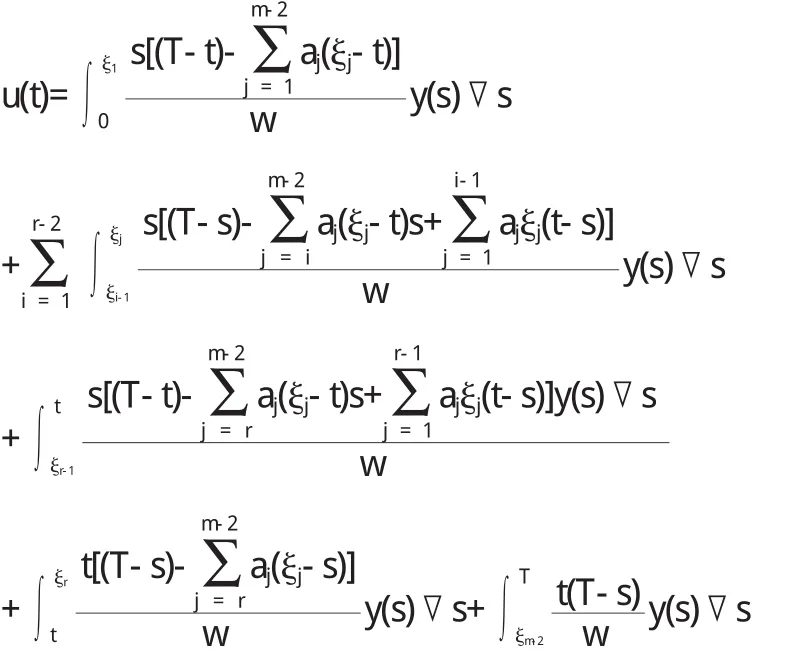
当t∈[ξm-2,T]时，由(5)式

由上可得结论.

引理3设w≠0，则(3)(4)的格林函数满足：G(t,s)≥G (T,s)，t,s∈[0,T]

引理4设w>0，则关于(3)(4)的格林函数G(t,s)>0，t,s∈[0,T]

证 根据引理3，只须证G(t,s)≥0

当s∈[0,ξ1]时

当s∈[ξi-1,ξi]时

当s∈[ξm-2,T]时

由上可知G(t,s)≥0证毕.

引理5设(H1)成立，则G(t,s)≤G(s,s)其中t,s∈[0,T]

证当t∈[0,T],s∈[0,ξ1],s≤t时，

当t∈[ξr-1,ξr](2≤r≤m);s∈[ξi-1,ξi](r≤i≤m-2),t≤s时

当t∈[0,T],s∈[ξm-2,T],t≤s时,

定理6设(H1)成立，则对固定s∈[0,T]，

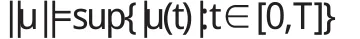
证根据引理5可知，||G(·，s)||=G(s,s)

当s∈[0,ξ1]时

当s∈[ξi-1,ξi]，2≤i≤m-2时

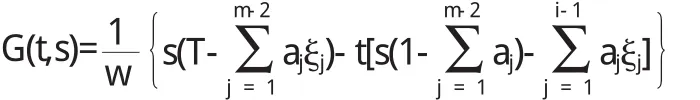
由于s∈[ξi-1,ξi]，那么

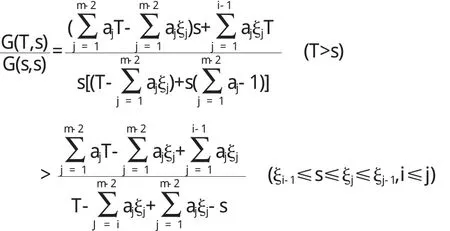
当s,t∈[ξm-2,T]时

情形1s≤t时

由ξj≤ξm-2≤s≤T,(j≤m-2)则

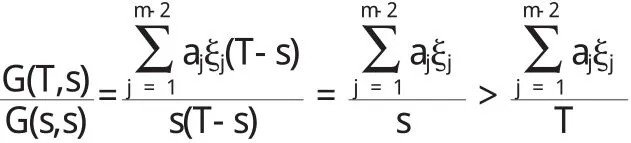
定理7设(H1)成立，设G1(t,s):=G(t,s)，G j(t,s)=G(τ,s)塄s(2≤j≤n)则Gn(t,s)是（-1）nu(△塄)n(t)=0 t∈[0,T]满足(2)的格林函数.

证 当n=1时易见成立，假设n=k-1成立，亦即Gk-1(t,s)

设u(△塄)(t)=v(t)那么

由假设

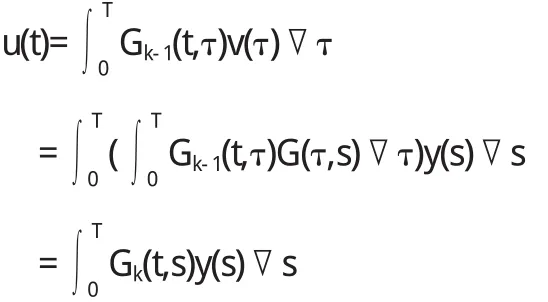
由上可知n=k时成立，证毕.

定理8设(H1)成立，则Gn(t,s)满足：

（1）0≤Gn(t,s)≤Ln-1||G(·,s)||t,s∈[0,T]

（2）Gn(t,s)≥mnLn-1||G(·,s)||t∈[ξm-2,T]s∈[0,T]

3 锥及泛函型锥拉伸压缩定理

定义9设E为实B a n a c h空间，若P是E中非空凸闭集且满足下列条件：

(1)u∈P,λ≥0,则λu∈P(2)u∈P,-u∈P则u=0（其中0为零元）

则称P为E中一个锥.

规定：α,γ:P→[0,+∞]连续，r,R为正实数.

P(γ,R):={u∈P:γ(u)

P(γ,α,r,R):={u∈P:γ<α(u)且γ(u)

下为泛函型锥拉伸压缩不动点定理，见［6］

引理10设P为实B a n a c h空间E中的锥，γ为P上非负连续泛函，P(γ,α,r,R)为P上的一个有界非空集全连续且若下列之一成立：

(1)当u∈鄣P(α,r)时α(A u)≤r.

当y∈鄣P(α,r)z∈鄣P(γ,R),λ≥1,μ∈(0,1]时

α(λy)≥λα(y)，γ(μz)≥μγ(z)，α(0)=0.

(2)当u∈鄣P(α,r)时α(A u)≥r.

当y∈鄣P(α,r)z∈鄣P(γ,R),μ≥1,λ∈(0,1]时

α(λy)≤λα(y)，γ(μz)≥μγ(z)，γ(0)=0.

则A至少有一个不动点u*使得r≤α(u*)且γ(u*)≤R

4 主要结果

我们把在[0,T]上左稠密点连续，右稠密点右极限存在泛函全体记为Cld[0,T]，记E=Cld[0,T]E为B a n a c h空间，其中

P:={u∈E:u(t)≥0,坌t∈[0,T]}，P为E中的锥,

定理11设(H1)成立，a∈Clα([0,T],[0,+∞)，若存在0

S t e p 2.若u∈鄣P(α,r)，则u(t)≤r，t∈[0,T].由引理8和(C1)

从而有α(T u)≤r.

S t e p 3.若u∈鄣P(α,r)，则u(t)≥R，t∈[ξm-2,T].由引理8和(C2)

S t e p 4.由γ(A u)≥R及||A u||≥γ(A u)≥R>0，则||A u||≥R>0

根据引理10可知，A至少有一不动点u*，使得r≤α(u*)且γ(u*)≤R.证毕.

在定理11为λ为定常数时(1)(2)存在正解的情形，我们再给出λ在某区间变动时(1)(2)存在正解的情形.设

定理12设(H1)成立，并且，则(1)(2)至少存在一个正解.

证明 只须要求满足定理11的(C1)(C2)即可

推论 设f满足超线性，并且有(H1)成立，则对任意λ>0，(1)(2)至少有存在一个正解.

〔1〕Ma R,Multiplicity results for a three-point boundary value problem at resonance,Nonlinear analysis,53(2003): 777-789.

〔2〕Zhang G.,Sun J,positive solutions of m-point boundary problems,J.Math.Anal APPL.,291(2004):406-418.

〔3〕Liu X.,Qiu J,three positive solutions for second-order m-point boundary value problems,APPL.Math.comput, 156(2004):733-742.

〔4〕Anderson D.,Avery R,An even-orderthree-point boundary value problem on time scales,J.Math.anal.APPL.,291(2004):514-525.

〔5〕Anderson D,solutions to second-order three-point problems on time scales,J.Difterence Equations and APPL.,8(2002):673-688.

〔6〕Avery R.,Anderson D,Fixed point theorem of cone expansion and compression of functional type,J.Differ,E-quationsAPPL.8(2002):1073-1083.

〔7〕Ma R,Positive solutions of a nonlinear m-point boundary value problem,computers Math. APPL.,42(2001): 755-765.

O 175

A

1673-260X（2012）10-0003-04