同科电子组态nlq与组态nl2(2l+1)-q的原子态
2012-09-01吕立君
吕立君
(赤峰学院 物理与电子信息工程学院,内蒙古 赤峰 024000)
同科电子组态nlq与组态nl2(2l+1)-q的原子态
吕立君
(赤峰学院 物理与电子信息工程学院,内蒙古 赤峰 024000)
在原子中,对于非同科电子组态,可按L-S耦合或j-j耦合推求其原子态.对于同科电子,由于泡利(Pauli)原理的限制,有些原子态不出现.学生在学习过程中不容易掌握同科电子组态到底存在哪些原子态,不理解同科电子组态nlq的原子态与组态nl2(2l+1)-q的原子态为什么相同.本文详细讨论同科P电子组态的原子态,直观地展示同科电子组态nlq的原子态与组态nl2(2l+1)-q的原子态相同.
同科电子;电子组态;原子态
1 引言
构成原子的每个电子都具有轨道运动和自旋运动,每一种运动又都处在其他运动的磁场中,因此它们的各种运动间会产生相互作用.如两个价电子的轨道运动和自旋运动分别为l1,s1;l2,s2,这四种运动之间将有六种相互作用:
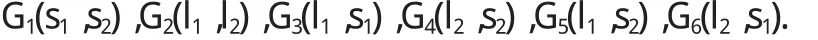
这六种相互作用的强弱是不同的,而且对于不同的原子情况也不同,一般G5(l1,s2),G6(l2,s1)较弱可忽略,其余四种相互作用的强弱程度不同.对于非同科电子,可按L-S耦合或j-j耦合推求其原子态.对于同科电子,由于泡利原理[1-4]的限制,有些原子态是不出现的.如氦原子的基态电子组态1 s 1 s、镁原子的基态电子组态3 s 3 s,在实验中从未观察到过3S1态.本文将详细讨论同科P电子组态的原子态,直观的给出同科电子组态n lq的原子态与组态n l2(2l+1)-q的原子态相同,同时可观测到原子中电子充满某个壳层或支壳时时原子的轨道角动量、自旋角动量、总角动量都为零.
2 泡利(Pauli)原理
泡利原理:不能有两个或两个以上的电子处在同一个状态.
对原子中的每个电子而言,电子有轨道运动l,轨道运动的空间取向由轨道磁量子数ml决定,电子还有自旋运动s,自旋运动的空间取向由自旋磁量子数ms决定.这样电子的状态可由五个量子数n,l,ml,s,ms标识.但各电子的自旋量子数s=是相同的,实际上四个量子数n,l,ml,ms就可以标识电子的状态.则泡利原理可理解为:在原子中不能有n,l, ml,ms四个量子数完全相同的两个或两个以上的电子存在.
3 同科P电子组态npq的原子态
3.1 同科P电子组态n p3的原子态

表13 个同科P电子组态MLmax
由表1可知MLmax=2

表23 个同科P电子组态MSmax
由表2可知MSmax=

表33 个同科P电子的可能状态
将表3转换成图1.
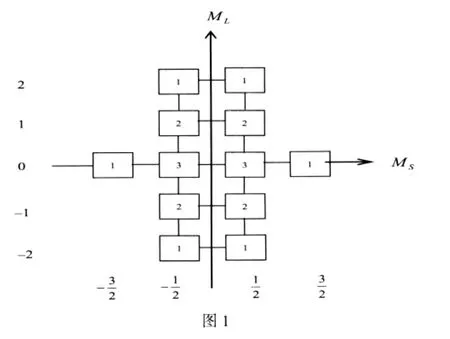
(1)在图1中将ML=±2,±1,0和与之相伴的MS=±取出可得图2.
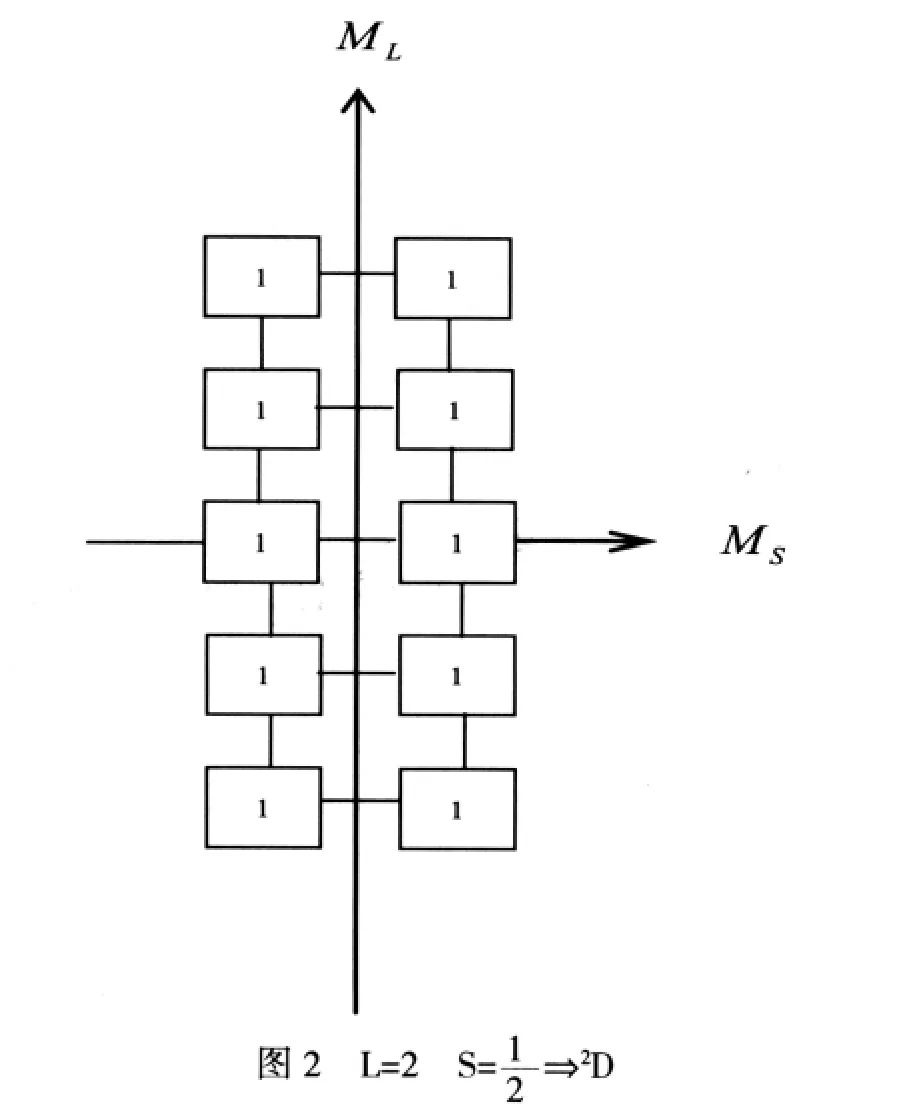
由图2可知:
ML=±2,±1,0圯轨道角动量量子数L=2圯原子态为D态
MS=±圯自旋角动量量子数S=
(2)在图1中将ML=±1,0和与之相伴的MS=±取出可得图3.
得到原子态2D.

由图3可知:
ML=±1,0圯轨道角动量量子数L=1圯原子态为P态
MS=±圯自旋角动量量子数S=
(3)在图1中将ML=0和与之相伴的MS=±,±取出可得图4.得到原子态2P.

由图4可知:
ML=0圯轨道角动量量子数L=0圯原子态为S态
MS=±,±圯自旋角动量量子数S=
得到原子态4S.由上述分析可知,同科p电子组态n p3的原子态为:4S,2P,2D.
3.2 同科电子n p4的原子态

表44 个同科P电子组态MLmax
由表4可知:MLmax=2

表54 个同科P电子组态MSmax
由表5可知:MSmax=1

表64 个同科P电子可能状态
将表6转化成图5.
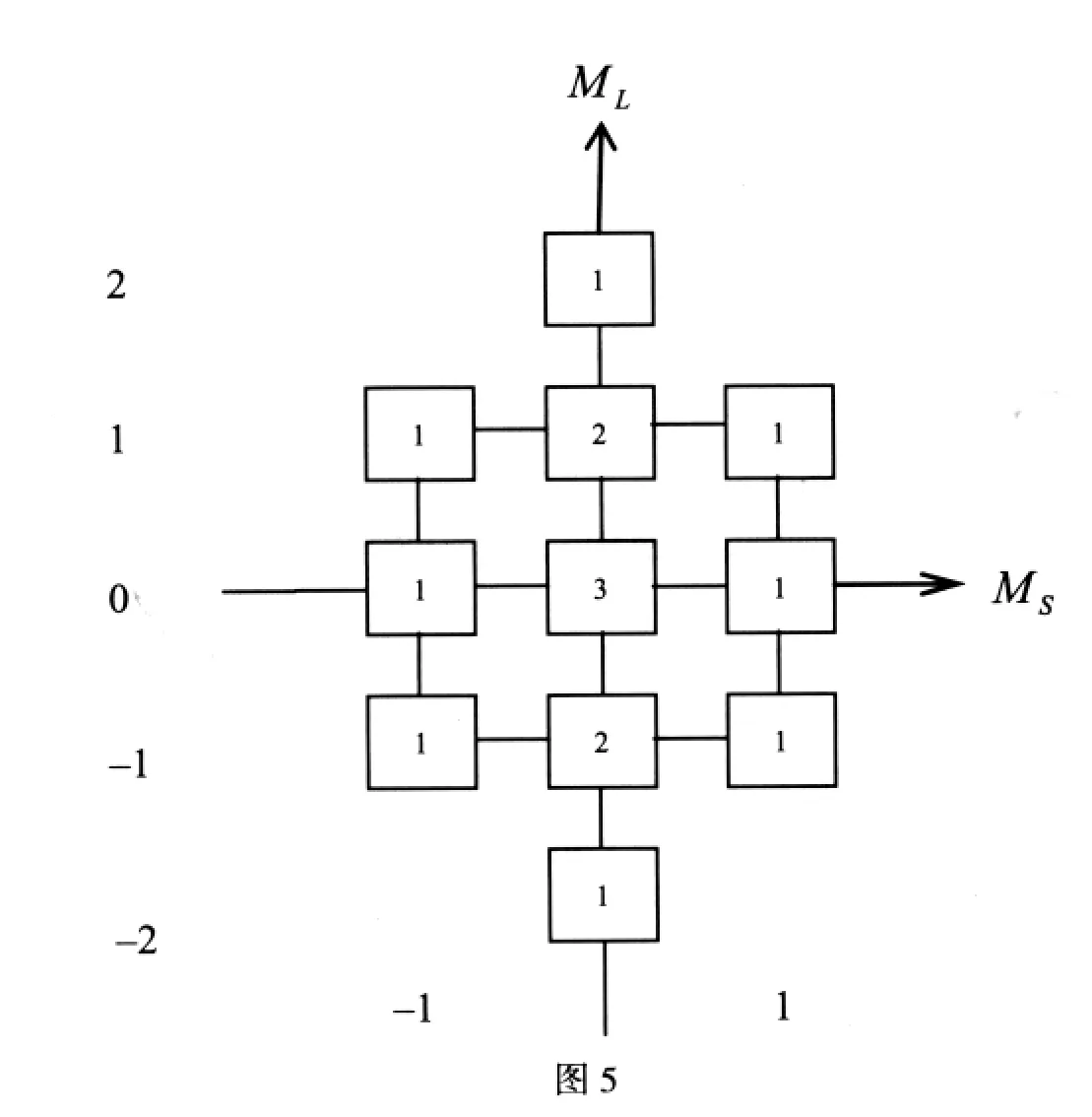

(3)在图5中将ML=0和与之相伴的MS=0取出可得图8.
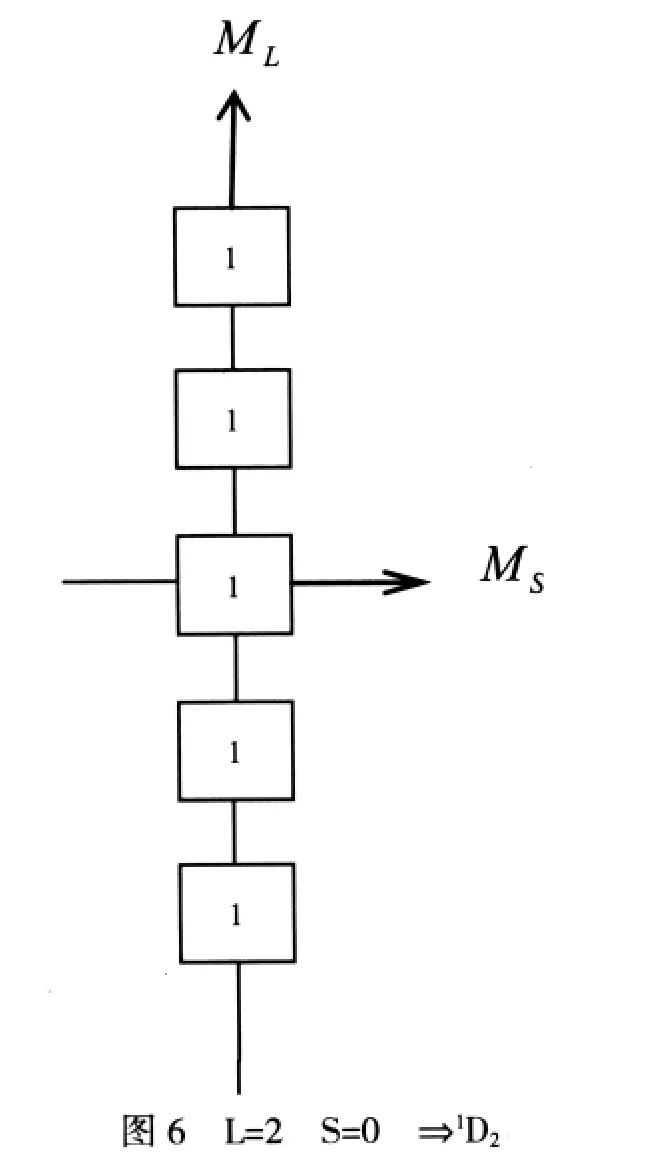
(1)在图5中将ML=±2,±1,0和与之相伴的MS=0取出可得图6.
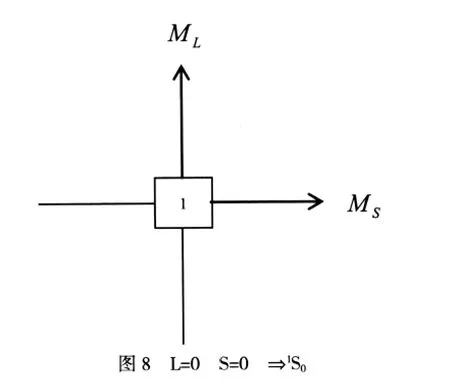
由图8可知:
ML=0圯轨道角动量量子数L=0圯原子态为S态
MS=0圯自旋角动量量子数S=0
得到原子态1S.
由上述分析可知,同科P电子组态n P4的原子态1S,3P,1D.
3.3 同科P电子组态n P5的原子态
由图6可知:
ML=±2,±1,0圯轨道角动量量子数L=2圯原子态为D态
MS=0圯自旋角动量量子数S=0
得到原子态1D.
(2)在图5中将ML=±1,0和与之相伴的MS=±1,0取出可得图7.
由图7可知:
ML=±1,0圯轨道角动量量子数L=1圯原子态为P态
MS=±1,0圯自旋角动量量子数S=1
得到原子态3P.

表75 个同科P电子态组态MLmax和MSmax
由表7可知:MLmax=1,MSmax=

表85 个同科P电子可能状态
将表8转化成图9.

由图9可知ML=±1,0与MS=±相伴.
由ML=±1,0圯轨道角动量量子数L=1圯原子态为P态
MS=±圯自旋角动量量子数S=
得到原子态2P.
由上述分析可知,同科P电子组态n P5的原子态2P.
3.4 同科P电子组态n P6的原子态

表96 个同科P电子组态MLmax和MSmax
由表9可知:
MLmax=0,MSmax=0
由表10可知:

表106 个同科P电子的可能状态
ML=0圯轨道角动量量子数L=0圯原子态为S态
MS=0圯自旋角动量量子数S=0
得到原子态1S.
由上述分析可知,同科P电子组态n P6的原子态1S.
4 结论
将文献[1,2]讨论结果及以上的分析结果列于表11.

表11 同科s电子、p电子的原子态
由表11可知,同科电子组态n lq的原子态与组态n l2(2l+1)-q的原子态相同.此外,对于电子填满s支壳、p支壳时原子的轨道角动量、自旋角动量、总角动量都为零,原子态都为1S0.
〔1〕杨福家.原子物理学[M].北京:高等教育出版社,2007.
〔2〕褚圣麟.原子物理学[M].北京:高等教育出版社,2010.
〔3〕顾建中.原子物理学[M].北京:高等教育出版社,1989.
〔4〕况蕙孙.原子物理学[M].北京:国防科技大学出版社,1995.
O 562
A
1673-260X(2012)06-0013-04
