中学数学中的几个渐近线问题及处理对策

☉江苏省昆山中学 戈 峰

中学教材中出现“渐近线”这个概念是在“双曲线的简单性质”这节中，概括为：曲线上的动点沿着曲线从某个方向向外延伸时，动点与某条直线无限地接近，但永远不相交，那么称此直线为曲线的渐近线（渗透极限思想）.中学数学的许多函数图像和曲线都有渐近线，例如教材中涉及到的初等函数：反比例函数、指对数函数、正余切函数等.学生在学习过程中若能领会渐近线的内涵，就能对掌握某些函数的形状、位置、大小等有很大的帮助.本文对中学数学中有渐近线的一些复杂函数进行讨论，并对处理有渐近线的函数问题提供几种策略.

一、分类讨论

除了教材中我们比较熟悉的反比例函数、指对数函数、正余切函数图像有渐近线外，我们经常碰到图像有渐近线的函数主要有分式函数型与超越函数型.

1.分式函数型.

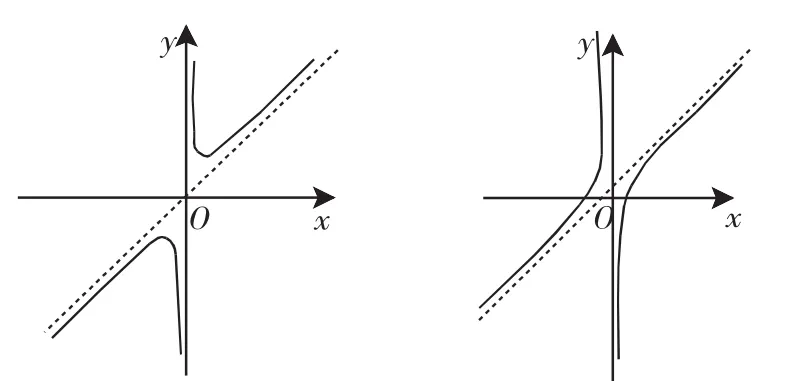
图1图2

以a>0，d>0，h>0进行分析：

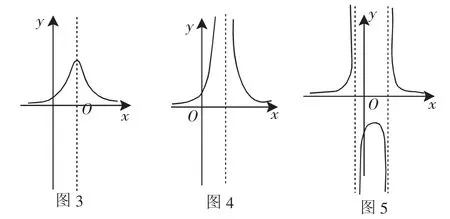
对于①，f（x）关于x=k对称，当x趋向于无穷时，a（x－k）2+h趋向于正无穷，则f（x）趋向于0，所以x轴是f（x）的渐近线.如图3.

对于②，f（x）关于x=k对称，当x趋向于无穷时，a（x－k）2趋向于正无穷，则f（x）趋向于0，当x趋向于k时，a（x－k）2趋向于0，则f（x）趋向于正无穷，所以x轴与x=k是f（x）的渐近线.如图4.

对于③，当x趋向于无穷时，a（x－m）（x－n）趋向于正无穷，则f（x）趋向于0.当x趋向于m和n时，a（x－m）（x－n）趋向于0，则f（x）趋向于正无穷，所以x轴、x=m与x=n都是f（x）的渐近线.如图5.

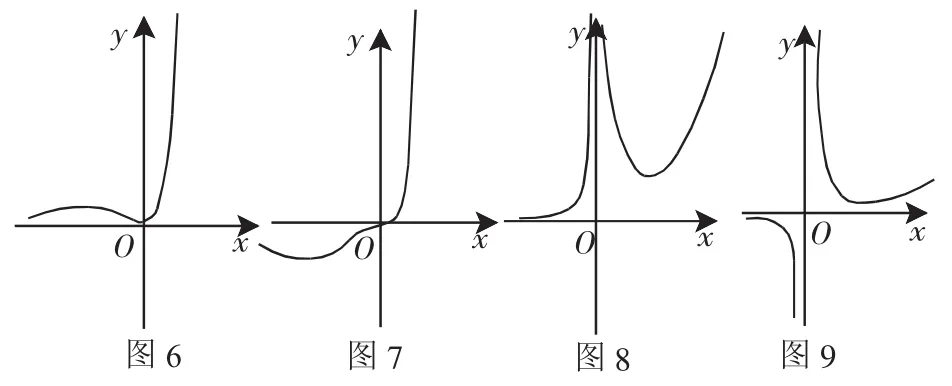
2.超越函数型.

（1）函数f（x）=xn·ex（n∈Z）.

当n=0时，f（x）=ex以x轴为渐近线；

当n>0时，f′（x）=xn－1·ex（n+x），易得f（x）在x=0处取得极小值，在x=-n处取得极大值；n为偶数时，f（x）在x=0处为拐点，在x=-n处取得极小值.而当x趋向于正无穷时，f（x）都趋向于正无穷.x趋向于负无穷时，f（x）趋向于0.所以f（x）=xn·ex以x轴为渐近线，如图6（n=2）和图7（n=3）.

二、应对策略

1.思想重视.

在学习函数性质时除了要重视函数的定义域、值域、单调性、奇偶性、对称性、特殊点等性质外，也要重视函数图像是否具有渐近线这一性质.

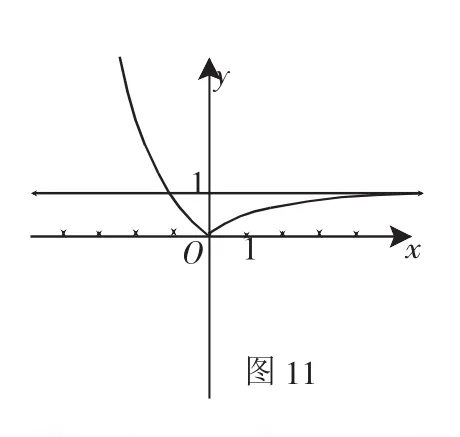
解析：画出图像如图11，图像的渐近线为y=1，要求y=m与y=有两个交点，所以m∈（0，1）.

2.取倒数.

解析1：方程的一个解为x=0.

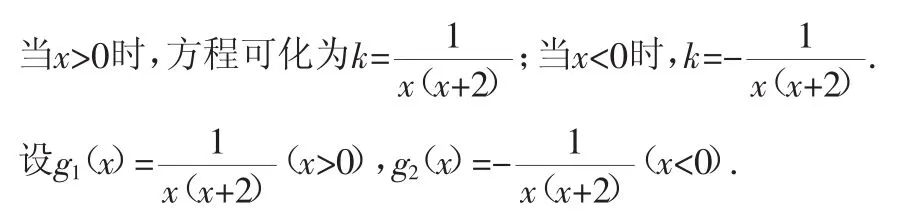
由分式函数型（2）讨论可知，x轴，y轴是g1（x）的渐近线；x=-2，x轴，y轴是g2（x）的渐近线.

因此g1（x）和g2（x）图像如图12.

所以当k>1时，有三个交点，即方程有三个解.又x=0是方程的解，所以当k>1时，方程f（x）=kx2有四个不同的实数解.

解析2：方程的一个解为x=0.

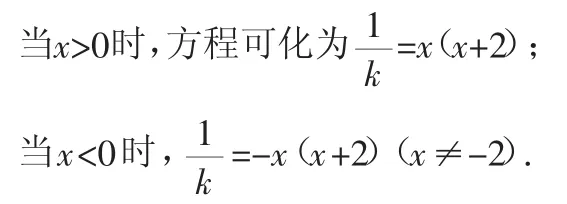
作出函数图像不难得到正确答案.通过取倒数，把分式函数化为整式函数，使复杂函数简单化，而且回避了渐近线，作图就不易犯错.

3.换元.

例3 讨论方程ax3-3x2+1=0的解的情况.

a=0，a=±2时方程有两解；a∈（-∞，-2）∪（2，+∞）时方程有一解；a∈（-2，0）∪（0，2）时方程有三解.

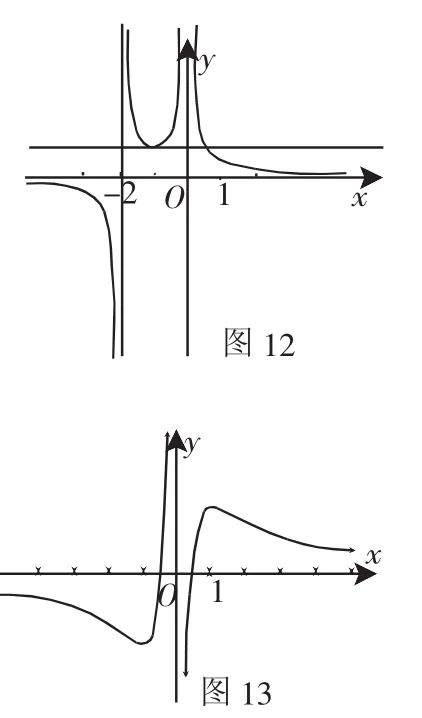
解析3：分析2虽然很直观，但图13还是很难画出来的，

特别是渐近线，很容易忽略.那么能否避免呢？

函数中的渐近线问题是学生在学习函数时比较容易忽视的，本文针对此问题列举了几类常见函数的渐近线和处理策略.