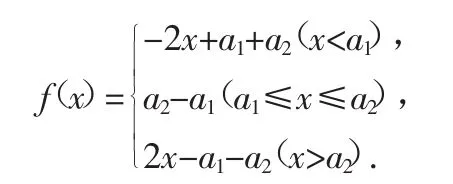对一道函数绝对值问题的探究

☉江苏省华罗庚中学 于亦香

绝对值问题一直都是高考的热点，其题目类型也十分丰富，遇到绝对值问题，我们通常的做法是去绝对值，或考虑其几何意义，笔者现就平时遇到的绝对值问题做如下探究，以期对读者有所帮助.

引例 已知f（x）=|x+1|+|x-a|关于x=1对称，则不等式f（x2-3）

解决这道题目之前我们先来探究f（x）=|x-a1|+|x-a2|+…+|x-an|（其中a1

当n=1，f（x）的图像就是将y=x-a1在x轴下方的图像翻折到x轴上方；

当n=2时，先去绝对值，故原函数可化为

根据以上4种情况的分析，我们归纳出更一般的情形.

结论：对于f（x）=|x-a1|+|x-a2|+…+|x-an|（其中a1

我们回过头来看上文的引例，f（x）=|x+1|+|x-a|的图像关于x=1对称，根据图像，我们发现x2-3到1的距离一定比x-1到1的距离近，且x-1不在［-1，3］之间，所以，我们可以得到以下关系：

本题中f（x）的图像正是上述探究中n=2的情形，有了这个结论作铺垫，题目解答就简单多了，如果再多一些绝对值呢？

已知函数f（x）=|x+1|+|x+2|+…+|x+2007|+|x-1|+|x-2|+…+|x-2007|，且f（a2-3a+2）=f（a-1），则a的范围是_________.

该题是n为偶数的情形，画出的图像一定是关于y轴对称的，所以有a2-3a+2=a-1或者

对于函数f（x）=|x-a1|+|x-a2|+…+|x-an|，我们还可以从绝对值的几何意义入手，如当n=2时，在数轴上依次取点A、B，以表示数a1、a2，f（x）表示数轴上一点P到A、B的距离之和.当P点在以A、B为端点的线段上时，PA+PB最小，为a2-a1；当n=3时，在数轴上依次取点A、B、C，以表示数a1、a2、a3，f（x）表示数轴上一点P到A、B、C的距离之和.当该点在以B处时，和最小，为a3-a1；当n=4时，在数轴上依次取点A、B、C、D，以表示数a1、a2、a3、a4，f（x）表示数轴上一点P到A、B、C、D的距离之和，当该点在以B、C为端点的线段上时，该和最小，为a4-a1+a3-a2.

利用绝对值的几何意义解题，显然可以简化运算，尤其对解决填空题很有帮助.

例1 |x-4|+|x-2|+|x-1|+|x|≥a对一切实数x成立，则a的最大可能值为_________.

解：解这道题时如果去绝对值，肯定浪费大家很多时间，如果我们考虑几何意义，那很快得出|x-4|+|x-2|+|x-1|+|x|的最小值为5，所以a≤5，即答案为5.

例2 在平面直角坐标系xOy中，设点P（x1，y1）、Q（x2，y2），定义d（P，Q）=|x1-x2|+|y1-y2|.已知点B（1，0），点M为直线x-2y+2=0上的动点，则使d（B，M）取最小值时的点M的坐标是___________.

以上几道题似乎是围绕着结论而设计的，因此只要我们吃透结论，那么很多问题我们解决起来就非常容易了.笔者写这篇文章不是要给出一个结论，而是希望同学们对平时遇到的问题不能做过或者会做就扔，我们要做一个有心人，收集相关题目，深入探究，挖掘问题的本质，这对于我们提高分析问题、解决问题的能力非常有用.