三角函数亮点扫描

☉江苏省灌南高级中学 苗 壮

近几年高考已逐步抛弃了对复杂三角变换和特殊技巧的考查，而重点转移到对三角函数的图像与性质的考查、对基础知识和基本技能的考查上来.

一、重中之重：形如y=Asin（ωx+φ）的图像和性质

（1）求函数f（x）的最小正周期和单调递增区间；

（2）函数f（x）的图像可以由函数y=sin2x（x∈R）的图像经过怎样的变换得到？

二、一大亮点：三角函数的最值与综合应用

例2已知函数f（x）=cos2x-2sinxcosx-sin2x.

（1）求函数f（x）的最小正周期；

（2）求函数f（x）的最大值、最小值.

三、年年必考：三角函数在三角形中的应用

三角函数在三角形中的应用，就是运用正弦定理、余弦定理、射影定理、三角形的内角和定理等，结合我们熟练的三角变形能力，解斜三角形、判定三角形的形状等.近几年高考对此类问题的考查有所侧重.

例3 △ABC中，内角A、B、C的对边分别为a、b、c，已知a、b、c成等比数列，且

由三角形的射影定理和正弦定理，得ccosA+acosC=b，则

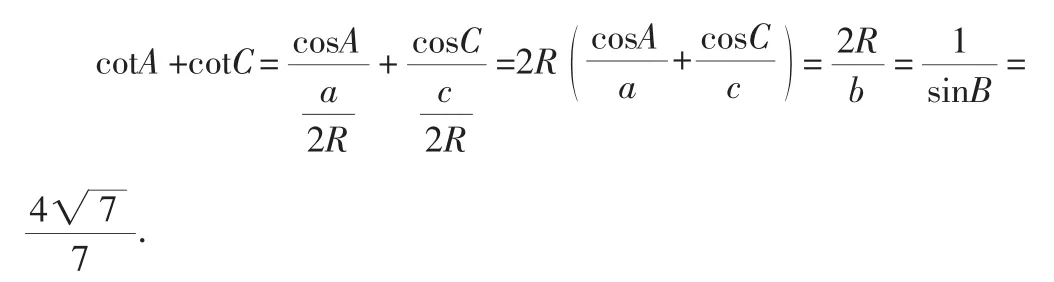
点评：本题是一个三角函数在三角形中的应用问题，考查正弦定理、余弦定理和三角函数的基本公式等基础知识，考查基本运算能力.解法1直接、简单，将正弦定理、余弦定理和三角函数结合得紧密无缝；解法2化角为边，思路清晰；解法3巧设公比，入手容易；解法4妙用射影定理整体计算求解.