西天山风对雪面升华量影响的实验研究——以中国科学院天山积雪雪崩研究站为例

林楚娟，熊良时

(1.重庆市环境保护工程设计研究院有限公司，广东 深圳 518055;2.深圳市深港产学研环保工程技术股份有限公司，广东 深圳 518055)

1 引言

中国西部高山带广泛分布的现代冰川，而冰川以下地区在冬季会积累大量季节性积雪。季节性积雪是普通降水的延迟，其融雪径流是干旱内陆河流域十分宝贵的淡水资源，在不同时间尺度上的变化对该地区河川径流的影响非常显著［1］。对于积雪的物质循环主要基于融雪水的估算和模拟［2］，而针对风对积雪的升华损耗鲜有研究。风速是影响雪面能量交换的重要参数，感热和潜热的收支状况都与风速大小有直接的关系。风速过大时造成风吹雪的发生，使得雪物质向地势低洼处搬运［3，4］。风吹过雪面时，风速随之降低，损耗的部分动能转化为热能输入雪层，加速雪面升华，积雪以水汽升华的相变形式而释放能量［5］。

西天山地区是我国西北干旱区多降水中心之一，积雪和冰川分布广泛。对于融雪期能量输入输出对积雪消融量估算研究颇多［6］。本文以地处西天山的天山积雪雪崩研究站为研究区，通过对雪面进行不同持续时间的吹风实验，从升华潜热的角度估算雪面升华量，将估算的升华量与实测量进行对比，探讨估算值与实际值误差产生的原因。

2 雪面水汽升华潜热估算方法

风吹雪面，雪面获得能量而升华，是一个由固相向气相转化的相变过程。雪面向大气中输送水汽而发生潜热交换，其水汽升华量△m取决于潜热变化量，其估算方法如下［7］:

式中:QE为潜热(kJ)，其估算方法如式(2)所示，hv为升华潜热(2.834kJ/g)，△m雪面的水汽升华量(g)。

式中:λv为蒸发潜热(2.5 ×103kJ/kg)，ρs为雪表面水汽密度(kg/m3)，视为饱和水汽密度，ρa为大气中水汽密度(kg/m3)，rv为水汽热交换阻抗(day/m)，本论文假定rv的估算方法如下［7］:

式中:zu为风速测量高度(2m)，zm为动力粗糙度参量(0.001m)，zT为气温测量高度(1m)，d为零水平面的替代高度(0m)，zh为热蒸发粗糙度参量(0.0002m)，k为 karman 常数(0.41)，u 为风速(m/s)。

利用水汽压和理想气体状态方程计算水汽密度，本论文采用冰面饱和水汽压替代雪面饱和水汽压，冰面饱和水汽压的估算最常用的是马格努尔(Magnus)经验公式:

E0=6.11hPa(t=0℃时，纯水平面上的饱和水汽压);t为气温(℃)。

3 实验方法

选择中国科学院天山积雪雪崩研究站(以下称积雪站)为研究区域，位于新疆伊犁地区新源县巩乃斯乡境内，积雪观测场海拔1776m，是新疆乃至整个中国西北干旱区的最大降水中心之一，冬季积雪深厚，有数十年的积雪研究历史和资料，是理想的研究试验区。1968～2009年，平均年降水量836.3mm，冬半年降水量约250mm，平均最大积雪深度87.2cm，而融雪集中于3月，积雪日数长的年份里融雪期能延长至4月中旬。

本实验于2010年1月在积雪站进行，此时为研究区的积雪期。以风速为6.4m/s的鼓风机作为人工控制风源，在积雪尚未开始时将6个孔径为0.1 mm雪筛放置于实验区，雪筛的直径为20 cm，降雪自然积于雪筛中，保持积雪的自然特性。每天实验时间为12:00～20:00，雪筛架设于鼓风机上方，对雪进行不同持续时间的吹风实验，记录风吹前后积雪的质量变化。对积雪分别吹风5 min(重复实验25次，平均气温为 －8.9℃)、10 min(15 次，平均气温为 －8.2℃)、15 min(15 次，平均气温为 －7.8℃)、20 min(5次，平均气温为 －6.8℃)、30 min(5 次，平均气温为 －7.9℃)和 60 min(5次，平均气温为 －9.6℃)。

4 结果与讨论

4.1 潜热的变化特征

潜热交换发生于雪面和大气之间，水汽密度差与风的作用使得雪面和水汽之间发生湍流交换。实验期间，利用实测气象数据估算潜热变化如图1所示，随着吹风时间的增加，潜热值也在不断上升，平均增长率为0.506 kJ/min。潜热交换不仅取决于吹风时间和风速，而且受水汽密度梯度影响，吹风30 min的实验中，潜热值在降低，因为实验中气温在不断下降，而60 min实验时潜热值却在不断上升，而此实验过程中气温在不断上升。气温的变化，造成水汽密度梯度的变化，所以估算的潜热也在不断变化之中。

图1 风吹雪面不同时间的潜热变化

4.2 水汽升华量的估计值与实测值对比分析

采用了两个常用的精度分析指标来评价模拟结果，无量纲的拟合优度系数Nash－Sutcliffe系数(R2)和质量差(Dm［%］):

式中:Δm为实测雪面升华量(g)，Δm'为相对应的估算所得雪面升华量(g)。

由式(1)估算的水汽升华量与实测值对比如图2。水汽升华量(Δm')的估算仅在变化趋势相对实际值(Δm)得到了较好的把握(R2=0.949)，而对于水汽升华量的总量估算却偏差较大，估计值总是低于实际值(Dm=27.1%)。

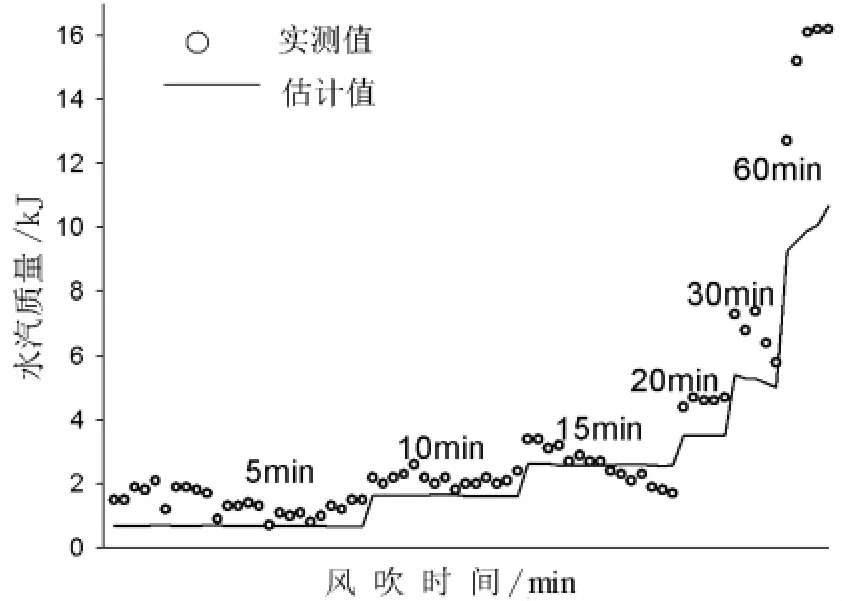
图2 水汽损耗的估计值与实际值对比

误差产生的原因有两点:一是水汽密度的估算采用了克拉伯龙方程，此方法将水汽假设为单一的理想气体，而且雪面水汽视为饱和水汽压，理想状态下的假设，使得水汽密度梯度的估算产生误差;二是升华潜热hv=2834J/g，此参数为常量，文献能量平衡融雪模型(UEB)中所公布参数来源于其他地区的研究结果［7］，所以在本研究区进行试用时，需要对参数hv进行校准。对于天山区风吹干寒型积雪的升华热研究，需要针对性较强的干寒型积雪升华热研究实验，有待后续更多的努力。

5 结语

通过实验，实测雪面水汽升华量，估算了潜热的变化状况，并利用潜热估算雪面升华量(Δm')与实际值(Δm)进行比较，主要结论为:风过雪面，随着风吹时间的增加，潜热值也在不断上升，但增长率较为稳定，平均增长率为0.506kJ/min。估算雪面升华量偏低于实际值(Dm=27.1%)，而对于升华量的变化趋势却得到了较好的把握(R2=0.949)。对于常量升华潜热hv的应用需要进一步校准和针对干寒型积雪的实验研究，估算出可适用于天山区干寒型积雪特性的升华热。

［1］Jansson P，Hock R，Schneider T.The concept of glacier storage:a review［J］.Journal of Hydrology，2003(282):116 ～129.

［2］庄毅璇.能量平衡融雪模型在西天山的应用试验［J］.安徽农业科学，2011，31(5):721～728.

［3］王中隆.中国风雪流及其防治研究［M］.兰州:兰州大学出版社，2001.

［4］汤 英.古尔班通古特沙漠融雪水文过程试验与模拟［D］.石河子:石河子大学，2008.

［5］Adam Winstral.Simulating wind fields and snow redistribution using terrain－based parameters to model snow accumulation and melt over a semi－ arid mountain catchment［J］.Hydrol Process，2002(16):3585～3603.

［6］赵求东，刘志辉.融雪模型研究进展［J］.新疆农业科学，2007，44(6):734～739.

［7］Quick M C，Pipes B C.Watershed Model［M］.Hydrological Sciences Bulletin，1977.