密集杂波环境下逻辑起始算法研究

刘 昇， 卢广山， 张晓鸿， 陈洪亮

(1.南京航空航天大学，南京 210016; 2.中国航空工业集团公司洛阳电光设备研究所，河南洛阳 471009;3.中航工业集团公司航空电子系统公司，北京 100028)

0 引言

航迹起始是目标跟踪的第一步，它是建立新的目标档案的决策方法，主要包括暂时航迹形成和轨迹确定两个方面，是目标跟踪领域中的首要问题。航迹起始的准则应是在虚警概率最小的情况下能正确起始目标航迹。由于航迹起始时，目标一般距雷达站很远，传感器探测分辨力低，测量精度差，加之真假目标的出现无真正的统计规律，因此在多目标航迹处理中，航迹起始是难以处理的问题［1－3］。与跟踪维持阶段的研究成果相比，这方面的研究成果较少，有关航迹起始算法性能分析方面的成果更少。对航迹起始算法进行性能分析的研究主要有:文献［6］中使用雷达实测数据对启发式规则方法、基于逻辑的方法、Hough变换法和改进Hough变换法等4种航迹起始技术进行了比较评价，分析了所用的雷达扫描次数对航迹正确起始性能的影响;文献［7］中使用统计学方法对上述4种算法的航迹检测概率和假航迹起始概率进行了理论上的推导和实验证明，从理论上说明了算法在不同杂波环境下的适用性。但文中并没有从理论或者评价指标上指出该算法为什么能在相同的杂波环境中获得比原有算法更好的起始性能。在实际应用中，逻辑法在虚警概率比较低的情况下可以获得有效的起始目标的航迹，但是在密集型杂波环境下性能急剧下降。本算法能在虚警概率比较高的情况下快速正确建立起始航迹，在工程应用中具有较大的实用价值。

1 算法综述

1.1 逻辑航迹起始算法

设Zj(i)表示传感器在第i个扫描周期接收到的第j个量测，T表示扫描周期。基于逻辑的航迹起始算法计算步骤如下。

1)将第1个扫描周期的所有量测Zj(1)(j=1，…，m)均建立为一条暂态航迹起始。设暂态航迹j的第一个点迹为Z(1)=［Zx(1)，Zy(1)］′，目标的估计速度大于Vmin而小于Vmax，如果第2个扫描周期的所有量测中有新的点迹Z(2)=［Zx(2)，Zy(2)］′落入如下关联区域1内

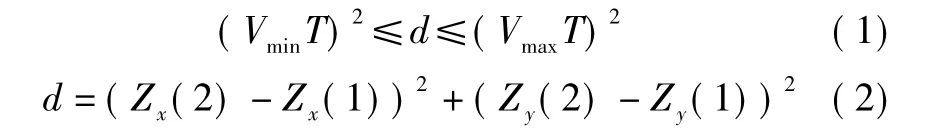
则认为该点与暂态航迹j的第1个点构成一个可能航迹o，此时航迹的目标状态为

否则，删除暂态航迹j。

2)在航迹起始阶段，目标距离雷达站比较远，一般作匀速直线运动，因此可能航迹o在第3个时刻的状态估计和量测预测为

若第3个扫描周期的量测中点迹Z(3)满足以下两个条件。

①以预测点位中心，建立椭圆关联区域2。

其中:S(3)=HP(3/2)HT+R，R为量测协方差;γ为误差门限，当观测维数nz=2时，γ=9.21。

② 设Z(3)与可能航迹 o的夹角为α，若α≤θ(θ一般由测量误差决定，为了保证以很高的概率建立起始航迹，可以选择较大)。

则认为量测Z(3)与可能航迹o关联。对于航迹o，如果有多个量测满足以上关联条件，则选择d(3)值最小的量测与航迹o关联，可能航迹转换为可靠航迹。

3)如果没有量测落入关联区域2中，则以预测状态作为目标在第3个扫描周期的状态，将航迹o外推一个点得，类似式(3)～式(5)预测在第4个扫描周期的状态和量测。判断第4个扫描周期的量测点迹Z(4)是否满足条件①和②，若有一个量测满足条件，则将该点与航迹o关联;若有多个量测满足上述条件，则将d(4)最小的量测与航迹o关联形成可靠航迹;若没有量测满足以上要求，则删除该条航迹。

4)在各个周期中不与任何航迹关联的量测用来开始一条新的可能航迹，转步骤1)。

注释:关于每条航迹，对暂态航迹采用关联域1进行互关联，对于可能航迹采用关联域2进行互关联。

该算法在航迹起始的第3)步中加入了对落入相关域中的量测与可能航迹是否关联的一个限制条件，从而保证了落入相关域中的量测应与可能航迹共线，确保航迹中不会存在V字形的航迹。

1.2 正确航迹建立概率

采用统计学方法对上述算法的航迹检测概率进行理论上的推导，在推导过程中采用3/4逻辑建立起始航迹。

由于远距离目标一般作匀速或匀加速直线运动，可认为目标从坐标原点开始沿x轴方向运动，因此目标在第i周期的量测为

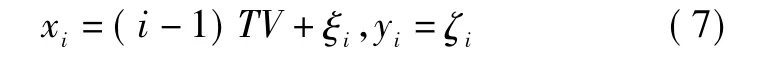
其中:ξi，ζi分别为x和y方向的测量误差，服从正态分布 N(0，σ2)。

在3/4起始逻辑下，正确航迹起始概率为

式中:Pd1是第1次扫描域中有一个点迹的概率;Pd2是第2次扫描中目标被检测，且落在关联区域1中的概率;是第3次扫描中目标被检测到且满足条件①、②的概率为第3次扫描中目标没有被检测到或目标检测到但不满足条件①、②，而在第4次扫描中目标检测到且满足条件①、②的概率。

由文献［4－5］可知，

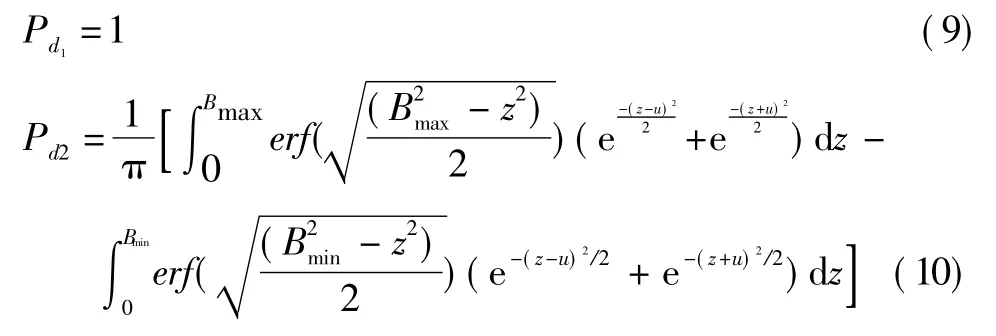
由式(6)确定的椭圆形区域，双轴分别为S11、S22(S是量测协方差)。设c=min(S11，S22)，当c≤VT×sin θ时，

当 c≥VT ×sin θ时，

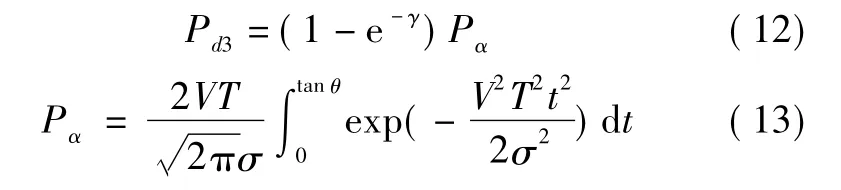
若考虑雷达扫描过程中的传感器漏检率pm，则航迹检测概率可表示为Pd=Pd1Pd2Pd3(1－pm)2。

1.3 虚假航迹起始概率

多目标跟踪环境中由于大量杂波和虚警的存在，除了影响目标航迹的正确起始，还会形成一些虚假航迹。分析过程中假设每周期数量和位置都是统计独立的，且每周期杂波数量服从泊松分布

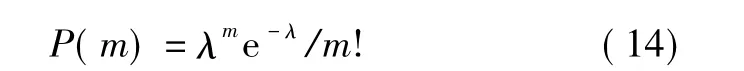
式中:λ表示期望的杂波数量。在扫描区域内，杂波位置服从均匀分布。

在3/4起始逻辑下，虚假航迹起始概率可表示为

Pf1是第1次扫描空域中至少有一个杂波点的概率;Pf2是第2次扫描中至少有一个杂波点满足条件①、②的概率是第3次扫描中至少有一个点满足条件①、②的概率为在第3次扫描中没有杂波点满足条件①、②，但第4次扫描中至少有一个杂波点满足的概率。

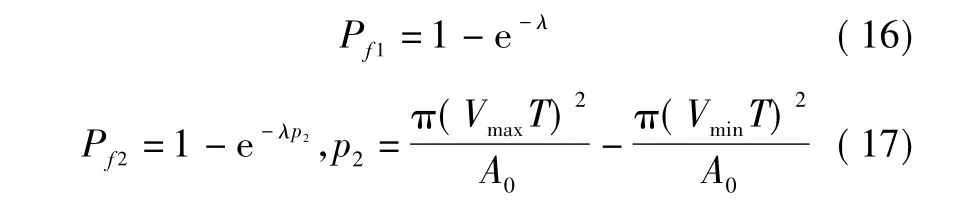
当 S≤VT ×sin θ时，

当 S≥VT ×sin θ时，

其中:A0表示扫描区域的面积。

2 实验仿真及分析

实验条件设定扫描范围为105m×105m，有5个目标均做匀速直线运动，5个目标的初始位置为(55000，55000)、(45000，45000)、(35000，35000)、(45000，25000)、(55000，15000)，速度 V=350 m/s，设置最大速度Vmax=4*V/3，最小速度Vmin=3*V/4，扫描周期为T=5 s，雷达的测向误差和测距误差分别为σθ=0.3°和σr=40 m。量测噪声标准差σ取100～1000 m，期望的杂波数量λ取100～1000。

取λ=100时，按上述方法在连续四个扫描周期内产生的杂波点与目标真实点的态势如图1所示。

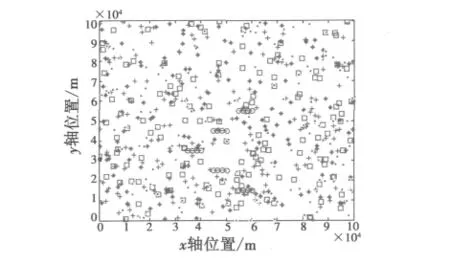
图1 杂波点与真实点的态势图Fig.1 Situation figure of clutter points and real points

对于图1的态势图，按3/4逻辑航迹起始方法起始的航迹见图2，本算法起始的航迹如图3所示。

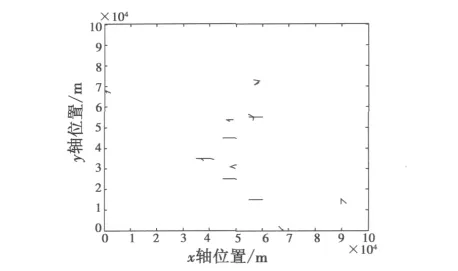
图2 3/4修正逻辑法起始的航迹图Fig.2 The figure based on modified three-out-of-four logic

在上述实验条件下，对本文方法和修正的逻辑航迹起始算法进行仿真，二者的正确航迹起始概率随噪声标准差σ的变化见图4，虚假航迹起始概率随杂波数量λ的变化见图5。

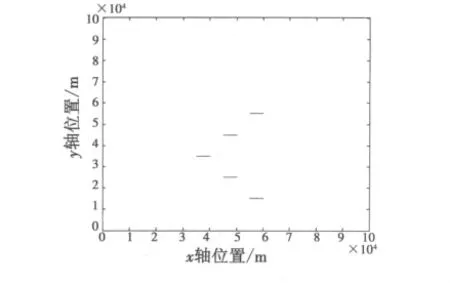
图3 新算法起始的航迹图Fig.3 The figure based on the new algorithm

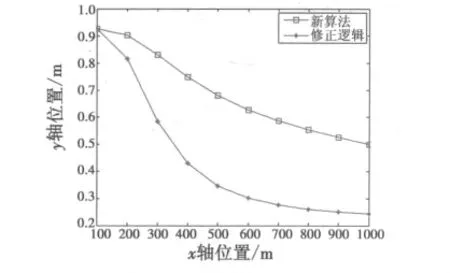
图4 正确航迹起始概率Fig.4 The figure of track detection probability

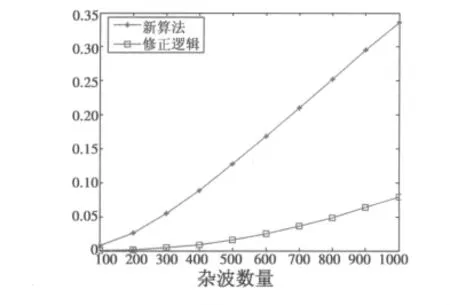
图5 虚假航迹起始概率Fig.5 The figure of false track probability

由图2和图3对比分析可知，本文方法比修正逻辑算法有更好的起始效果，图4显示了两种算法随噪声标准差σ增加时的正确航迹起始概率。在稀疏杂波环境下，两者的航迹检测概率相近。但是当噪声误差较大时，本文的方法有更高的正确航迹起始概率。由图5可见，随着杂波数量λ的增加，两种算法的虚假航迹起始概率都呈上升趋势，但相比而言，本方法具有很低的虚假航迹起始概率，更适用于杂波较高的环境。

3 结语

本文采用的航迹起始算法结合航迹处理，通过统计学方法对其正确航迹起始概率和虚假航迹起始概率进行理论推导，经过实验仿真证明，该方法具有很好的航迹起始性能，更适用于工程应用。

［1］ 贺鹏，白亮.快速随机Hough变换航迹起始算法［J］.电光与控制，2010，17(5):26-29.

［2］ 董志荣，论航迹起始方法［J］.情报指挥控制系统与仿真技术，1999(2):1-6.

［3］ 王国宏，苏峰，毛士艺.杂波环境下基于Hough变换和逻辑的快速航迹起始［J］.系统仿真学报，2002，14(7):874-876.

［4］ 罗鹏飞，张文明.一种多目标跟踪航迹起始新算法及其性能评估［J］.国防科技大学学报，1999，21(6):51-54.

［5］ LIU Sheng，LU Guangshan.A new algorithm of track initiation for multiple targets and performance analysis［C］//International Conference on Multimedia and Computational Intelligence，2010:339-341.

［6］ LEUNG H，HU Z.Evaluation of multiple target tracking initiation techniques in real radar tracking environment［J］.IEEE Pro-Radar，Sonar Nuving，1996，143(4):246-254.

［7］ HU Zhijian，LEUNG Henry.Statistical performance analysis of track initiation techniques［J］.IEEE Transactions of Signal Processing，1997，45(2):445-456.