改进正弦算子的弹道交接自适应算法
2012-08-27田宏亮梁晓庚贾晓洪李记新
田宏亮, 梁晓庚, 贾晓洪, 李记新
(中航工业空空导弹研究院,河南洛阳 471009)
0 引言
组合制导利用不同导引律的最佳性能,可以使导弹的抗干扰能力和在复杂作战条件下的作战效能得到明显提高,然而组合制导存在的最大技术问题是导引律交接时弹道的平滑过渡。平滑过渡就是要求不同导引律的弹道在交接点的弹道切线矢量相等。因为不同导引律的弹道是不同的,能满足该条件导引律的弹道接点是固定的;但实际上在任何条件下导弹随时都有可能要求弹道交接,所以找到适用于所有制导律的弹道交接算法就具有实际意义。文献[1]提出了弹道交接和交接段制导的新概念,并给出了零基交接和自适应交接制导算法。在此基础上,文献[2-3]分别在自动驾驶仪及弹体动力学为一阶和二阶环节的情况下,对交接算法参数的选择进行了研究。文献[4]对雷达寻的导引头的末制导体制进行了研究。
正弦函数作为过渡算子的自适应交班制导律[5]与用一次函数作为过渡算子比较可知,前者的航向积累误差小。本文对基于正弦算子的弹道交接自适应算法的正弦算子进行改进,得到一种新的弹道交接算法,其航向积累误差更小。
1 问题的描述
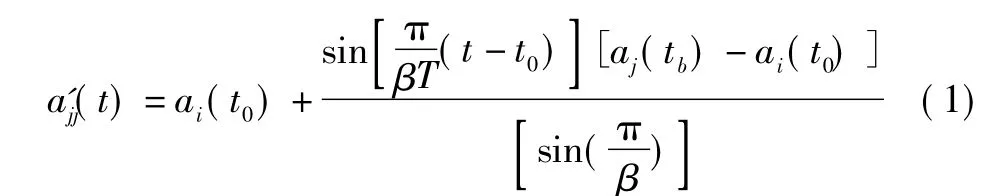
其中:∞ > β >2,t∈[t0,t0+T]。显然,t=t0时,,经过时间
2 弹体时滞参数对算法参数的影响
现在的问题是如何选择交接段参数T以保证交接段顺利实现。为了便于分析,仅考虑导弹某一通道的制导问题,这样制导指令为标量。考虑自动驾驶仪及弹体动力学为一阶环节G(s)的简单情况,如式(2)所示。
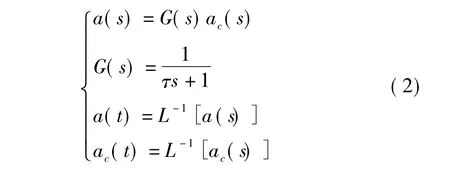
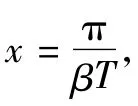
1)ai(t0),它是原始输入;
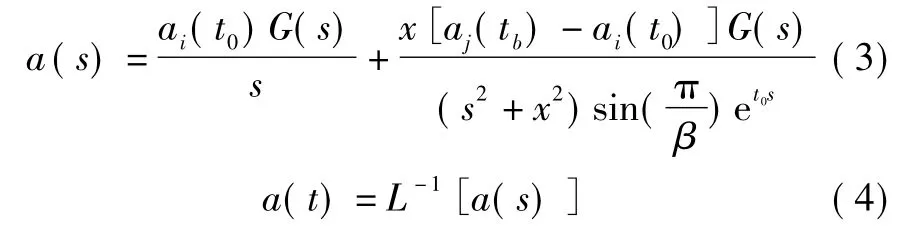
显然下式成立。
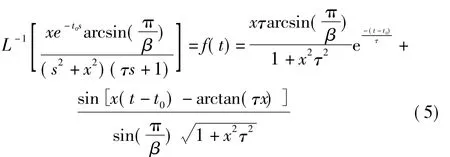
将式(5)代入式(4),得式(6)。

通常t0>T,若算法参数T满足T>>τ,则当 t=t0时,由式(6)得,a(t)≈ai(t0);当 t=t0+T 时,a(t)≈aj(tb)。
由以上分析知,当T>>τ满足时,基于改进正弦算子的弹道交接自适应算法可以实现弹道过渡交接班。
3 算法参数的选择
在交接导引段,弹道交接会产生一定的航向误差。令弹道弹道角速度为

式中:a(t)为导弹加速度,Vm为导弹速度;aj(tb)是理想的末制导加速度,则交接段的加速度误差Δa(t)为
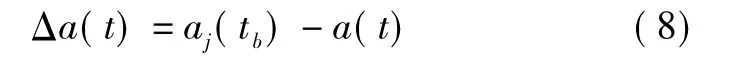
在交接班时间对式(8)积分,并考虑到T>>τ,可得:
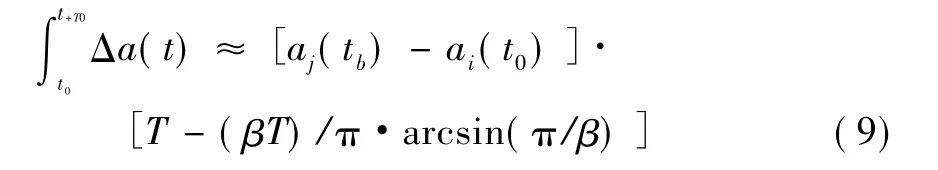
根据式(7)可得在T>>τ条件下,积累的弹道航向误差为
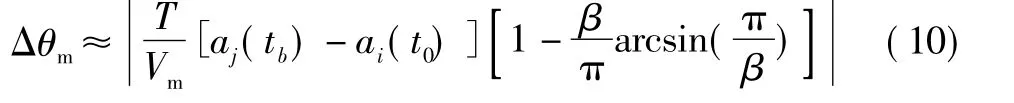

考虑极端情况下最大航向误差,设导弹最大加速度为 amax,最大容许航向误差为 Δθmax,Δamax为交接班指令最大误差。
当β=2.82时,当选择 T满足式(11)时,Δθ≤Δθmax成立。

4 仿真分析
下面对所得算法进行仿真验证。
在初制导段和中制导段用比例制导律。末制导段目标通常会大机动,由于变结构制导律[6-7]和鲁棒制导律[8-11]有很好的抗目标大机动能力,所以在末制导中用文献[9]设计的制导律作为末制导律。

图1 后向追击时的弹目相对距离变化图Fig.1 Missile-target relative distance under the condition of chasing
设弹目相对距离为25 km;导弹初始速度为950 m/s;导弹最大加速度为50g;目标初始速度为250 m/s,并且进行8g的机动;弹道交接常数T设为2。在相同的初始条件下,对照正弦弹道交接算法和改进正弦弹道交接算法进行了后向追击的数字仿真,结果如图1所示,在用正弦弹道交接算法时,后向追击下的脱靶量为9.3 m;在用改进正弦弹道交接算法时,后向追击下的脱靶量为1.3 m。结果表明,在用改进正弦弹道交接算法时,弹道更平滑,脱靶量更小。
5 结束语
为了实现不同制导段间的弹道平滑过渡,本文对不同制导律间的指令交接导引段设计进行了研究,提出了一种新的弹道交接自适应算法,即基于改进正弦算子的弹道交接自适应算法,并给出了算法参数的取值范围。这个算法优于基于正弦算子的弹道交接自适应算法。虽然这里给出的参数取值范围是在比较简单情况下得到的,但这些条件可作为设计时的参考依据。
[1] 侯明善,刘怀勋,张金鹏.中远距战术导弹复合制导的交接规律[J].电光与控制,1998,5(4):14-17.
[2] 张金鹏,刘怀勋,侯明善.自适应交接律在复合制导弹道交接中的应用[J].制导与引信,1999(4):18-21.
[3] 周德兵.弹道交班自适应算法研究[J].上海航天,2007(5):31-34.
[4] 罗喜霜,张天桥.多用途导弹中末段交班研究[J].弹道学报,2001,13(4):47-50.
[5] 王延.近距空空导弹中末制导交接班策略研究[D].西安:西北工业大学,2006.
[6] 刘永善,刘藻珍,李兰忖.攻击机动目标的被动寻的模糊变结构制导律研究[J].系统工程与电子技术,2007,29(2):254-258.
[7] 佘文学,周凤岐,周军.非线性变结构制导律[J].宇航学报,2003,24(6):638-641.
[8] 张晨光,陈大融.拦截机动目标的一种鲁棒末制导律设计[J].清华大学学报:自然科学版,2007,47(8):1300-1303.
[9] 郭建国,周军.基于H∞控制的非线性末制导律设计[J].航空学报,2009,30(12):2424-2427.
[10] CHEN B S,CHENY Y,LIN C L.Nonlinear fuzzy H∞guidance law with saturation ofactuators against maneuvering targets[J].IEEE Transactions on Control Systems Technology,2002,10(6):769-779.
[11] YANG C D,CHEN H Y.Three-dimensional nonlinear guidance law[J].Int J Robust Nonlinear Control,2001,11(2):109-129.
